基于接入点的泰森多边形指纹聚类定位算法*
吕 娜,单志龙,张 凡,余刘勇
基于接入点的泰森多边形指纹聚类定位算法*
吕 娜,单志龙*,张 凡,余刘勇
针对KNN指纹定位算法定位耗时长和基于K-Means聚类的KNN指纹定位算法定位精度不稳定的问题,本文提出了一种以接入点为离散点生成泰森多边形,利用泰森多边形对指纹聚类,然后使用最强接入点法确定移动节点的定位区域,最后通过动态KNN算法进行定位的指纹聚类定位算法。实验表明,该算法能有效缩短定位时间并提高定位精度,在接入点数量变化时表现出较好的定位性能,且在不同定位区域中性能具有较好的普适性。
指纹定位算法;接入点;泰森多边形;KNN;K-Means
移动通信业的迅速发展与移动终端的普遍使用使得基于位置服务LBS(Location Based Services)受到越来越多的关注,并被广泛应用于人们的生活中。虽然GPS技术发展成熟,可以为LBS解决许多室外定位问题,但其受卫星信号无法穿透墙壁等因素的影响,在障碍物较多、环境复杂的室内并不适用[1]。而人类超过80%的活动时间是在室内度过,市场对室内基于位置服务有很大需求,如特殊人群监护、矿井人员定位、超市导购等[2-4]。
室内定位方法主要有两类[5]:一类是通过测量信号的到达时间TOA(Time of Arrival)、到达时间差TDOA(Time Difference of Arrival)或到达角度AOA(Angle of Arrival),运用三边测量法对移动节点进行定位。该类方法定位精度较高,但需要额外硬件测量信号传播的时间或方向,对室内定位系统的成本和定位范围提出了挑战[6]。另一类方法是基于接收信号强度指示值RSSI(Received Signal Strength Indication)定位。通常地,基于RSSI的定位方法包括基于信号传播模型定位算法和指纹定位算法[7]。信号传播模型定位算法因信号在传播过程中严重受到多径效应、信号衰减和延迟失真等因素的影响及模型中的参数值依赖建筑物的结构和使用的材料而不能满足人们对定位系统高精确度、低计算复杂度和快速响应的要求;指纹定位算法自RADAR系统出现以来,已成为当今室内定位的主流算法[8]。
指纹定位算法包括离线训练和在线定位两个阶段[1]。在离线阶段需完成构建指纹库的工作,通过对指纹聚类,可减少在线阶段的指纹匹配量,大大降低计算复杂度,提高算法定位效率;在线阶段则通过匹配算法如KNN、KWNN、SVM、深度学习[9-12]等将待定位点与指纹库中的指纹进行匹配,估计待定位点位置。该类算法的定位性能虽仍受环境因素影响,但思路简单,且不受参数作用,通过对算法两个阶段的改进,可以有效提高定位精度和速度。
为减少定位时间,本文提出基于接入点的泰森多边形指纹聚类定位算法VAPFC(Voronoi Based on Access Point Fingerprint Clustering)。该算法引入泰森多边形,以接入点AP(Access Point)作为泰森多边形的离散点来构建单元格,从物理位置上用各单元格对指纹分类,然后找到待定位点所属指纹子类,选取满足误差阈值条件的指纹对待定位点进行定位。
1 指纹定位算法
指纹定位算法是一种基于场景的定位方法,分为离线训练和在线定位两个阶段。
在离线阶段,通过在定位场景中部署N个发射无线信号的AP,按照一定间隔设置参考点并测量其信息,建立包括参考点坐标(x,y)及其接收到的来自N个AP的RSSI值(RSSI1,RSSI2,…,RSSIN)的指纹库。
在在线阶段,通过测量待定位点的RSSI信息,以RSSI向量作为比较对象,运用匹配算法将待定位点与指纹库中的指纹进行匹配,以相似性高的指纹坐标作为待定位节点的位置。常用的匹配算法分为确定性匹配算法、概率性匹配算法及神经网络算法,其中确定性匹配算法中的KNN算法原理简单,计算量相对较少。
1.1 KNN指纹定位算法
KNN指纹定位算法(K-Nearest Neighbor Algorithm)是将在待定位点处实时观测的RSSI向量与指纹库中所有指纹的RSSI向量进行相似度测量,选取对比结果中前K个相似度高的指纹估计待定位点位置。相似度常以欧氏距离衡量:
(1)
式中:D(αi,β)表示指纹库中第i个指纹αi的RSSI向量与待定位点β的RSSI向量的距离,距离越小,相似度越高。αij、βj分别表示αi、β接收到的来自第j个AP的RSSI值。
假设指纹库中有M(M>K)个指纹。将D1,D2,…,DM升序排序形成新序列S(S1,S2,…,SM),则待定位点β的位置(xβ,yβ):

(2)
式中:xSi和ySi分别表示新序列S中第i个指纹的横坐标和纵坐标。
1.2 基于K-Means聚类的KNN指纹定位算法
指纹量较大时,传统的KNN指纹定位算法对移动点定位的响应延时较长,因此很多学者提出通过对指纹聚类和减少指纹匹配量来提高定位效率[10,13-16]。K-Means就是其中一种常用的聚类方法[16],运用K-Means对指纹库聚类的过程如下:①随机选取K个指纹作为初始聚类中心;②计算其余每个指纹到各聚类中心的距离,按最小距离原则将各指纹聚类到距它最近的中心;③计算每个类簇的均值,并将均值作为新的聚类中心;④重复步骤②和步骤③,直到所有指纹到其相应聚类中心的距离之和J最小或迭代次数达到要求为止。
在线定位时,首先计算待定位点与各个聚类中心的距离,然后确定距离待定位点最近的聚类中心,最后选取该中心所属类别中的指纹进行KNN定位。
K-Means定位算法思想简单,并弥补了传统算法定位效率低的缺陷,但聚类数K值由经验确定且初始聚类中心是随机选取的,这种随机性和不可靠性使得算法的运行效率对初始聚类中心敏感,且定位精度过度依赖聚类初始条件。因此,如能利用固定的AP对指纹聚类,减少算法对初始聚类中心的敏感性,则有可能提高定位算法的性能。
2 VAPFC定位算法
2.1 VAPFC算法的离线聚类分析
1911年,荷兰气候学家Thiessen A H首次将泰森多边形应用于气象学,以离散分布的气象站的降雨量衡量各气象站所属大区域的平均降雨量[17]。自此,泰森多边形的以下特性在诸多领域得到了应用[18-19]:①每个泰森多边形内部只有一个离散点;②泰森多边形内的点到相应离散点的距离最近;③位于泰森多边形边上的点到其两边的离散点距离相等;④离散点的特征代表了其对应泰森多边形内部点的整体趋势。
为提高定位速度,基于泰森多边形特性,以AP作为离散点,运用泰森多边形生成算法将定位场景划分为与各AP相对应的N个子区域,即V1,V2,…,VN,将M个指纹按照物理位置聚类到各子区域中。
VAPFC定位算法实现指纹聚类的过程如下:
2.1.1 区域分割
借助泰森多边形与德洛内三角网DT(Delaunay Triangulation)的关系可实现泰森多边形生成算法,即:泰森多边形的顶点是DT中各相应三角形的外接圆圆心,而DT中三角形的顶点是泰森多边形的离散点,其具体步骤如下:
①初始化DT
DT的构建需要一个足够大的初始三角形dt0,定位区域Dl×w属于dt0,记初始DT0={dt0},dt0=((10 000,-10 000),(-10 000,-10 000),(0,10 000))。
②构建DT
将N个AP逐个部署在Dl×w中。部署APi后,首先找到包含APi的三角形Ti,利用APi和Ti获取三角形集合TSi,APi位于TSi中所有三角形的外接圆内;其次将Ti与TSi中的三角形进行合并得到多边形Ci;最后将APi与Ci的所有顶点相连即可得到DTi。DTN生成后,构建DT完成。
③确定每个离散点的相邻三角形
三角形t1,t2,…,tk的共同顶点为V,则称这k个三角形是点V的相邻三角形。
dti∈DT,Vij∈dti若Vij∉G,则U(Vij,G)
(3)
式中:dti表示DT中第i个三角形,Vij是dti的第j个顶点,G是离散点标记集合,其初始值G0={(10 000,-10 000),(-10 000,-10 000),(0,10 000)}。若Vij不在G中,则将Vij加入G,记为U(Vij,G)。
ST(Vij,dti)={st0,st1,st2,…,stk-1}
(4)
式中:ST(Vij,dti)表示离散点Vij的所有相邻三角形的集合,dti是该集合的初始元素,记为st0,k表示Vij的相邻三角形的个数。
④计算离散点的相邻三角形的外接圆圆心
GCVij={GC(st1),…,GC(sth),…,GC(stk)},
sth∈ST(Vij,dti)
(5)
式中:GCVij表示离散点Vij的所有相邻三角形的外接圆圆心的集合,sth是集合ST(Vij,dti)中的第h个三角形,GC(sth)表示三角形sth的外接圆圆心。
⑤生成泰森多边形
将式(5)中GCVij集合里的所有点相连即得离散点Vij对应的泰森多边形。将N个AP对应的泰森多边形集合记为VS={VS1,VS2,…,VSN}。
根据上述步骤,可以实现区域的泰森多边形分割,如图1所示,分别以V1、V2、V3和V4为离散点的4个泰森多边形将整个平面进行了无重叠地分割。这4个离散点是DT中的两个三角形V1V2V3和V1V3V4的顶点,而两个三角形的外接圆圆心A和B是泰森多边形的顶点。

图1 泰森多边形与DT网的关系展示图
2.1.2 指纹信息录入
将M个指纹的信息fp1((x1,y1),(RSSI11,RSSI12,…,RSSI1N)),…,fpM((xM,yM),(RSSIM1,RSSIM2,…,RSSIMN))录入定位系统中。
2.1.3 指纹聚类
定位区域分割后,把每个泰森多边形单元格作为一个类区域,位于该类区域中的指纹属于同一类簇。如果指纹库中第i个指纹fpi的物理位置位于第j个AP对应的泰森多边形VSj内部,则将fpi聚类到VSj中,记为Cluster(fpi,VSj),即:
若In(fpi,VSj),则Cluster(fpi,VSj)
(6)
2.2 VAPFC算法的在线定位分析
在线定位时,首先通过确定待定位点RSSI向量中的最大值找到其所属定位子区域,然后运用动态KNN匹配算法估计待定位节点的位置。
2.2.1 定位子区域的获取
目标点接收到的信号强度值与无线信号收发双方的距离成一定的对数关系[20],表示为传播路径损耗模型:

(7)
式中:P(d)表示目标点与信号发射端的距离为d时接收到的信号强度,P(d0)表示距离为d0时接收到的信号强度,n是与定位环境相关的路径损耗指数,XdBm服从N(μ,σ2)分布。
由式(7)可知,待定位点处接收到的信号强度P(d)越大,则待定位点距离信号发射端越近。记待定位点为U,其RSSI向量中的最大值为RSSIj,则距离U最近的接入点为APj。因泰森多边形特性(2),故U的定位子区域是以APj为离散点的泰森多边形VSj。
2.2.2 位置估计
假设VSj中包含L个指纹,使用KNN指纹定位算法计算U的坐标,即首先利用式(1)计算出U与L个指纹的距离序列D(D1,D2,…,DL)的值,然后将D升序排序得到新序列S(S1,S2,…,SL)及S对应的指纹序列fp(fp1,fp2,…,fpL),最后将fp中前K个指纹作为参考点,使用式(2)估计U的位置。但KNN算法中K值固定,对于变动的待定位点而言,参与计算的指纹量可能过多或过少,这两种情况都会导致定位精度下降。Beomju等[21]也提出运用KNN算法定位的精度与K值的选定相关。为得到更高的定位精度,故在线定位过程中采用设定误差门限值T的方法动态选取K,具体的在线定位流程如图2所示。

图2 VAPFC算法在线定位流程
合适的T值对获得较准确的位置估计至关重要,故当以下两种情况出现时应对T值及时进行调整:
①S1大于T
S1为VSj中所有的指纹与U的距离中的最小值。S1大于T,表明VSj中不存在满足阈值条件的指纹,故将与U相似度最高的fp1加入指纹选择集以估计待定位点的位置。若经过对多个移动点定位后发现,在S中均找不到小于T的值,说明T的设定值过小,此时应以当前T值为准线T0,以ΔT为正增量,对T值进行上浮调整,记为Ti(i=1,2,…),直到存在Si小于T,且找到使算法的平均定位误差达到最小的T值为止。本文中以2为T0,ΔT取0.5,确定T取值区间为[3.5,4.0],再以3.5为T0,0.1为ΔT,确定T的取值为3.7,如表1所示。
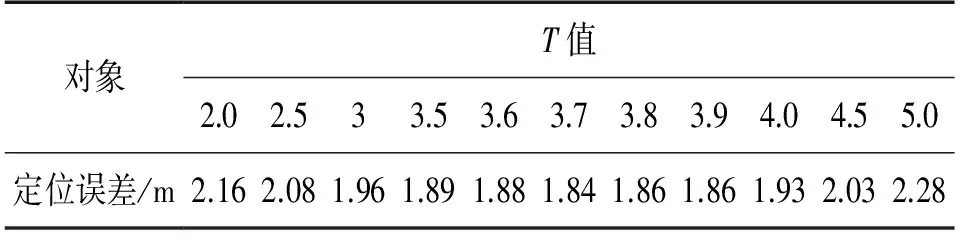
表1 T值对动态KNN算法的平均定位误差的影响
②存在Smaxi
Smaxi表示S中小于T的最大值,将S1,S2,…,Si对应的指纹均加入指纹选择集中。为避免T值过大导致定位误差增加,应对当前T值下的定位误差进行考量。若定位误差较大,则极有可能是由T取值偏大从而使得相似度较低的参考点进入指纹选择集造成的,故应对T值进行下降调整并同时观测定位误差的变化,该过程与①中T值修正过程正相反。
3 仿真实验及结果分析
算法的仿真实验在MyEclipse平台下进行,仿真结果图由MATLAB软件绘制,仿真场景为:40 m×40 m的正方形区域,区域内均匀部署4个AP,除去4个顶点每5 m布置一个指纹,品红色三角形代表AP,黑色点代表指纹,如图3所示。
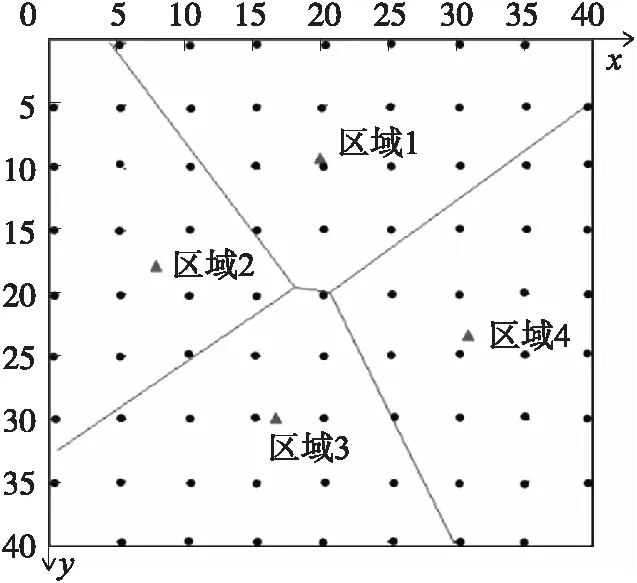
图3 40 m×40 m仿真场景图
在该场景下,首先对传统的KNN指纹定位算法、基于K-Means聚类的KNN指纹定位算法和VAPFC算法的定位精度和定位时间进行了比较,然后分析了聚类中心、AP数目和定位区域等的变化对定位误差和定位耗时的影响。
①定位精度和定位时间的比较分析
对3种定位算法各进行5次仿真,每次仿真设置10 000个待定位点,将5次仿真结果求均值得3种算法的定位误差与定位时间,如表2所示。

表2 3种算法的定位误差与时间比较
由于K-Means定位算法与VAPFC定位算法在定位时均缩小了参考点的匹配范围,故与传统定位算法相比,K-Means定位算法的定位速度大幅提高,但定位精度下降较大;VAPFC定位算法在定位精度上虽比传统定位算法降低约15%,但其缩短了约89%的定位时间,符合“在保证一定定位精度的前提下,提高定位时效性”的研究意图;此外,VAPFC定位算法在定位时间上与K-Means定位算法持平,但K-Means定位算法受聚类中心随机性的影响,其定位精度远低于VAPFC定位算法。
②聚类中心对定位误差的影响分析
为探究聚类中心对3种算法定位误差的影响,在实验①的仿真场景中进行10次仿真,仿真结果如图4所示。在所有仿真参数都不变的情况下,传统算法因无聚类过程且直接从所有指纹中选择K个最佳指纹进行定位,故其定位精度比其他两种算法高,定位误差稳定;K-Means定位算法受其随机生成的初始聚类中心影响,定位结果波动较大;VAPFC算法以固定的AP为中心对指纹进行聚类,定位结果波动不大,具有较好的稳定性。

图4 3种定位算法在10次仿真中的定位误差(m)

图5 3种定位算法在不同AP数目下的定位误差(m)
③AP数目影响分析
当定位场景中的AP数目发生改变时,需要重新部署AP,假定指纹位置不变但其RSSI向量值随AP变化,则算法的定位性能也会随着变化。
图5显示,AP数量增加,传统定位算法与VAPFC算法的定位误差差距较稳定,但K-Means定位算法与其他两种定位算法的误差差距逐渐缩小,说明K-Means定位算法的定位精度受AP数目影响较大,这与K-Means算法的聚类效果对其聚类数K敏感有关;在AP数目相同时,VAPFC算法的定位误差始终小于K-Means定位算法,说明该算法相对于K-Means定位算法可得到更高定位精度。
图6显示,随着AP数量的增加,传统定位算法因每个指纹信息量增加且在线时没有减少指纹匹配量,定位耗时逐渐增加;VAPFC定位算法的定位耗时逐步减少至平稳状态;K-Means定位算法的定位耗时受匹配聚类中心时间与匹配选定类别中指纹时间的关系影响。当AP数量小于10时,匹配指纹时间比匹配聚类中心时间对K-Means定位算法的定位耗时影响更大,算法的整体定位时间逐步减少;当AP数量大于10时,情况正相反。

图6 3种定位算法在不同AP数目下的定位时间(s)
通过对图5、图6的分析可知,AP数量对3种定位算法的定位误差及时间均有影响,尤其对传统算法的定位时间和K-Means定位算法的定位误差影响最大;VAPFC定位算法在定位精度上比传统定位算法降低约15%,但定位速度远高于后者;在AP数目较小时,VAPFC定位算法的定位耗时与K-Means定位算法持平,定位精度远高于后者;在AP数目较大时,VAPFC定位算法的定位精度与K-Means定位算法持平,定位速度远高于后者。总体而言,无论AP数目大小,VAPFC算法在定位精度和定位速度上均有优势。
④定位区域影响分析
为验证VAPFC算法是否具有普适性,我们对100 m×100 m,200 m×200 m和400 m×400 m的定位区域进行了仿真。从仿真结果图7~图9可知,在不同的定位区域中,当AP数目增加时,3种算法的定位误差和定位时间的总体变化趋势均与将3种算法在40 m×40 m定位区域中仿真得到的结果规律基本一致,故VAPFC算法具有较好的普适性。

图7 100 m×100 m定位区域中3种定位算法在不同AP数目下的定位误差(左)和定位时间(右)
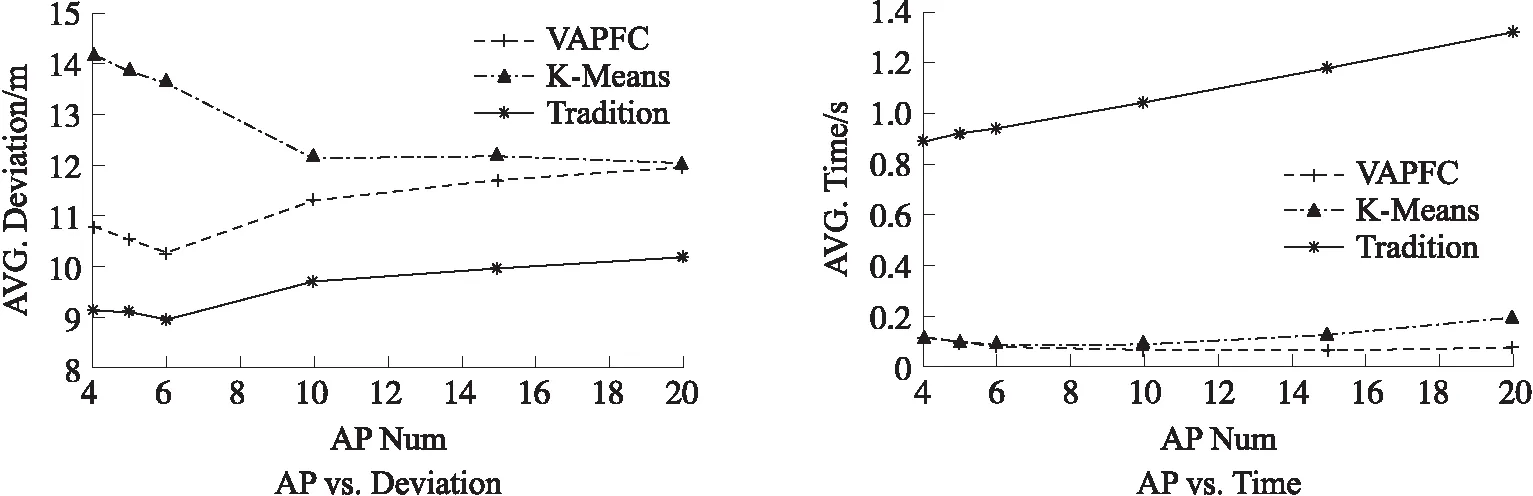
图8 200 m×200 m定位区域中3种定位算法在不同AP数目下的定位误差(左)和定位时间(右)

图9 400 m×400 m定位区域中3种定位算法在不同AP数目下的定位误差(左)和定位时间(右)
4 总结
本文提出了一种估计室内移动点位置的指纹定位算法,该算法运用泰森多边形的特性,通过以AP点为离散点、利用各AP对应的泰森多边形对指纹库聚类、运用最强AP法将待测点位置锁定到某一子区域、采用动态KNN算法对待测点位置进行估计。仿真结果表明,所提算法VAPFC在有效缩短定位时间的同时保证了定位精度,定位结果具有较好的稳定性和区域普适性。
[1] 李燕君,徐凯锋,邵剑集. 利用众包更新Wi-Fi室内定位指纹库的方法研究[J]. 传感技术学报,2014,27(12):1692-1698.
[2] 邓中亮,余彦培,袁协,等. 室内定位现状与发展趋势研究(英文)[J]. China Communications,2013,10(3):50-63.
[3] 李论,丁恩杰,郝丽娜,等. 一种改进的煤矿井下指纹定位匹配算法[J]. 传感技术学报,2014,27(3):388-393.
[4] 陈斌涛,刘任任,陈益强,等. 动态环境中的WiFi指纹自适应室内定位方法[J]. 传感技术学报,2015,28(5):729-738.
[5] 郭红成,罗海勇,尹浩,等. 基于线性插值和动态指纹补偿的分布式定位算法[J]. 传感技术学报,2009,22(12):1795-1801.
[6] 孙利民,李建中,陈渝. 无线传感器网络[M]. 北京:清华大学出版社,2005:141-146.
[7] 刘晓叶,徐玉斌. 基于自适应射频指纹地图的WSN室内定位算法研究[J]. 传感技术学报,2015,28(8):1215-1220.
[8] 唐文胜,李姗,匡旺秋. RF室内定位指纹库空间相关生成算法[J]. 计算机工程与应用,2008,44(23):226-229.
[9] Zhao Y,Liu K,Ma Y,et al. An Improved KNN Algorithm for Localization in Multipath Environments[J]. EURASIP Journal on Wireless Communications and Networking,2014,2014(1):208.
[10] Chen W,Chang Q,Hou H T,et al. A Novel Clustering and KWNN-Based Strategy for Wi-Fi Fingerprint Indoor Localization[C]//International Conference on Computer Science and Network Technology. 2015:49-52.
[11] Wu T F,Lin C J,Weng R C. Probability Estimates for Multi-Class Classification by Pairwise Coupling[J]. Journal of Machine Learning Research,2004,5(4):975-1005.
[12] Wang X,Gao L,Mao S,et al. CSI-Based Fingerprinting for Indoor Localization:A Deep Learning Approach[J]. IEEE Transactions on Vehicular Technology,2017,66(1):763-776.
[13] 都伊林. 一种模糊聚类KNN位置指纹定位算法[J]. 微型机与应用,2012,31(23):55-58.
[14] He C,Guo S,Wu Y,et al. A Novel Radio Map Construction Method to Reduce Collection Effort for Indoor Localization[J]. Measurement,2016,94:423-431.
[15] 刘春燕,王坚. 基于几何聚类指纹库的约束KNN室内定位模型[J]. 武汉大学学报(信息科学版),2014,39(11):1287-1292.
[16] 陈国良,张言哲,汪云甲,等. WiFi-PDR室内组合定位的无迹卡尔曼滤波算法[J]. 测绘学报,2015,44(12):1314-1321.
[17] Thiessen A H. Precipitation Averages for Large Areas[J]. Monthly Weather Review,1911,39(7):1082-1084.
[18] 戴波,李志超,刘学君,等. 基于泰森多边形的UWB危化品堆垛仓储货物定位技术[J]. 化工学报,2016,67(3):878-884.
[19] 赵春江,吴华瑞,刘强,等. 基于Voronoi的无线传感器网络覆盖控制优化策略[J]. 通信学报,2013(9):115-122.
[20] Noh S I,Lee W J,Ye J Y. Comparison of the Mechanisms of the ZigBee’s Indoor Localization Algorithm[C]//Ninth Acis International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing. IEEE Computer Society,2008:13-18.
[21] Shin B,Lee J H,Lee T,et al. Enhanced WeightedK-nearest Neighbor Algorithm for Indoor Wi-Fi Positioning Systems[C]//International Conference on Computing Technology and Information Management. 2012,2(2):574-577.
VoronoiBasedonAccessPointFingerprintClusteringLocalizationAlgorithm*
LÜNa,SHANZhilong*,ZHANGFan,YULiuyong
(Schoolof Computer Science,South China Normal University,Guangzhou 510631,China)
To solve the problems of long position time-consuming in KNN fingerprint localization algorithm and unstable accuracy inK-Means clustering based localization algorithm,a novel fingerprint clustering localization algorithm is proposed. This algorithm considers APs as Voronoi diagram’s generators to create Voronoi cells,uses these cells to cluster fingerprints of database and a method based on the biggest
signal strength to find out the positioning subarea of mobile nodes,and estimates the location of mobile node by automatic KNN algorithm. Experiment results reveal that this algorithm sharply reduces position time-consuming,improves the accuracy,and has a good performance when the quantity of AP changes. With the location area altering the performance still exists.
fingerprint localization algorithm;AP;Voronoi diagram;KNN;K-Means
10.3969/j.issn.1004-1699.2017.12.026
项目来源:国家自然科学基金项目(61671213,61370003);广东省自然科学基金项目(2015A030313395);广东省科技计划项目(2013B040401014)
2017-05-04修改日期2017-07-18
(华南师范大学计算机学院,广州 510631)
TP393
A
1004-1699(2017)12-1941-07
吕娜(1993-),女,硕士研究生,主要研究方向为物联网、无线传感器网络;
单志龙(1976-),男,教授,博士,博士生导师,主要研究方向为物联网、无线传感器网络、移动互联网、计算机与通信网等,zhilongshan@gmail.com。

