带消失位势Choquard方程解的存在性

蔡明建

(中南民族大学 数学与统计学学院,武汉430074)

带消失位势Choquard方程解的存在性

蔡明建

(中南民族大学 数学与统计学学院,武汉430074)

研究了一类非局部Schrödinger方程解的存在性.运用山路引理和Ekland变分法，利用泛函几何结构和极小化序列得到了方程解的存在性.首次将半线性椭圆方程的相关结果推广到Choquard型消失位势Schrödinger方程.

Choquard方程；山路引理；Ekland变分法；消失位势

1 主要问题及结果

本文考虑一类带消失位势Choquard方程：

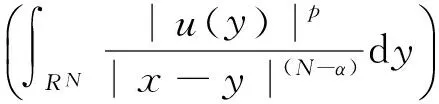
(1)

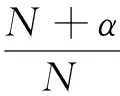
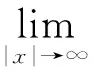
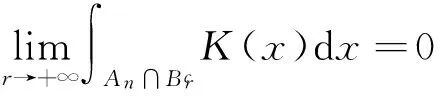
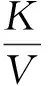
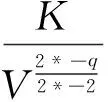
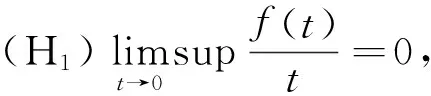
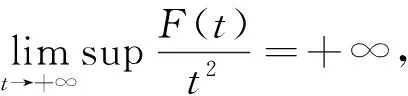
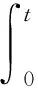
Choquard型方程解的存在性的研究，近年来一直吸引着研究者的兴趣.文[3]中Moroz和Schaftingen考虑了基态解的存在性，文[4]讨论该类方程解的存在集中性，其他相关解的存在性问题见文[5-7].本文的主要结果是定理1.

定理1 假设条件(i)～(ⅳ)，(H1)～(H4)成立,那么方程(1)在D1,2(RN)中至少存在两个非平凡解.

2 预备知识

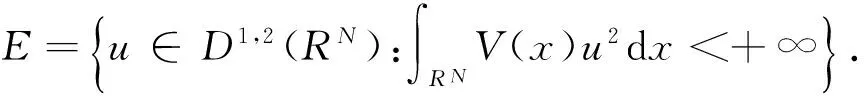
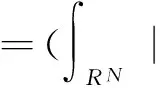
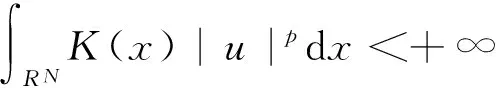
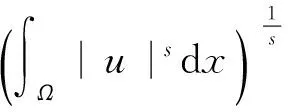
与方程组(1)所对应的能量泛函可以写为：

其中

由Hardy-Littlewood不等式[8]知：

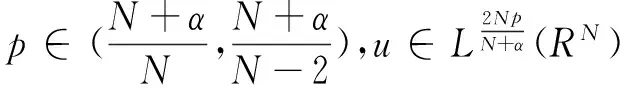
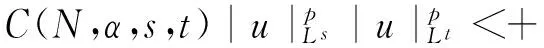
(2)

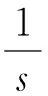
当u∈E满足：

设E为一实的希尔伯特空间，泛函I∈C1(E,R).我们说{un}为I的P.S.序列:如果当n→∞时,有I(un)→c,I′(un)→0.泛函I在指标c∈R处满足P.S.条件是指,上述{un}存在一个收敛的子序列.若I(u)=c,I′(u)=0时，称u为I在E上的临界点，c为I的临界值.

引理1I∈C1(E,R)且I满足：

(1) 存在β,ρ>0使得I(u)≥β对任意‖u‖=ρ时都成立；

(2) 存在e∈E,‖e‖>ρ且使得I(e)<0.

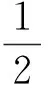
由此可知,存在足够小的ρ>0使得‖u‖=ρ时：

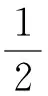
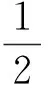
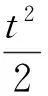
由此可知当t→+∞时，I(tu)<0成立，故证存在e∈E,‖e‖>ρ且使得I(e)<0.

3 定理1的证明

在这一部分将证明主要结果定理1.

引理2 如果(i)～(ⅳ)，(H1)～(H4)成立，则有I满足P.S.条件.

证明1)任取{un}⊂E满足I(un)→c并且I′(un)→0,那么{un}有界.

事实上：

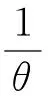
由条件(H4)可知存在c1，使得：

因此：

c(1+‖u‖)≥k‖u‖2-c1,可知{un}有界.

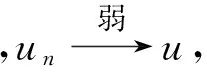
‖un-u‖2=I′(un)-I′(u),un-u-K(x)(f(un)-f(u))(un-u)dx-Q(un-u,un-u)dx.

由文[1,2],有：

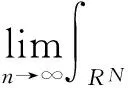
(3)

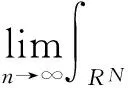
(4)

n→∞时，

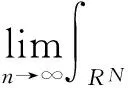
(5)

由文[9]有：

(6)

这里当n→∞时，

I′(u)-I′(un),un-u→0.

(7)

由(5)～(7)式可知n→∞时，‖un-u‖→0.

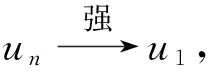
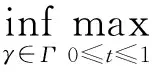
综上可知，方程(1)在D1,2(RN)中至少存在两个非平凡解u1,u2.

[1] Alves C O, Souto M A S. Existence of solutions for a class of nonlinear Schrödinger equations with potential vanishing at infinity[J]. J Differential Equations, 2013,254(4):1977-1991.

[2] Li Q, Teng K, Wu X. Existence of positive solutions for a class of critical fractional Schrödinger equations with potential vanishing at infinity[J]. Mediterr J Math, 2017,14(2):14.

[3] Moroz V, Schaftingen J V. Ground states of nonlinear Choquard equations: Existence,qualitative properties and decay asymptotics[J]. J Funct Anal, 2013,265:153-184.

[4] Lv D. Existence and concentration of solutions for a nonlinear Choquard equation[J]. Mediterr J Math, 2015,12(3):839-850.

[5] Deng Y, Shuai W. Positive solutions for quasilinear Schrödinger equations with critical growth and potential vanishing at infinity[J]. Commu Pur Appl Anal,2017,13(6):2273-2287.

[6] Deng Y, Lu L, Shuai W.Constraint minimizers of mass critical Hartree energy functionals: Existence and mass concentration[J]. J Math Phys, 2015,56(6):249-261.

[7] 康东升，熊 萍，曹玉平.含有多重临界指数和Hardy项的双调和非线性方程组解的存在性[J].中南民族大学学报(自然科学版)，2016,35(2):146-150.

[8] Hardy G H, Littlewood J E. Some properties of fractional integrals[J]. Math Zeitsehr,1928,27:565-606．

[9] Wang T. Existence and nonexistence of nontrivial solutions for Choquard type equations[J]. Electron J Diff Equ,2016(3): 1-17.

[10] Ekeland I.On the variational principle[J]. J Math Anal Appl, 1974,47:324-353.

ExistenceofSolutionsofChoquardTypeEquationswithVanishingPotentials

CaiMingjian

(College of Mathematics and Statistics,South-Central University for Nationalities, Wuhan 430074,China)

In this paper，a class of nonlocal Schrödinger equations were studied. The Mountain Pass Lemma and Ekland variational principle were used to prove the existence of solutions. Some new results about Choquard type Schrödinger equations with vanishing potentials were obtained by related results in the semilinear elliptical equations.

Choquard type equations; Mountain Pass Lemma；Ekland variational principle；vanishing potentials

2017-09-12

蔡明建(1981-)，男，讲师，博士，研究方向：偏微分方程，E-mail: cmj9904@mail.scuec.edu.cn

中央高校基本科研业务费专项资金资助项目(CZQ12014)

O175.25

A

1672-4321(2017)04-0149-03