界面应力传递重新分析及Cohesive模型参数的确定

， ，

(天津大学 机械工程学院 力学系，天津 300072)

界面应力传递重新分析及Cohesive模型参数的确定

王坎盛，沈珉，于济菘

(天津大学机械工程学院力学系，天津300072)

在经典剪滞理论中引入双线性cohesive模型表征纤维/基体之间的非理想界面，重新分析了纤维增强复合材料中的应力传递机理，得到了考虑界面因素的应力分布。用上述结果解释了单丝段裂实验过程中的现象，讨论了界面参数和材料性能对应力分布的影响。基于上述理论，建立了用cohesive单元表征界面的模拟单丝段裂实验的三维有限元模型，结合单丝段裂实验结果，提出了一种估测cohesive界面刚度参数的新方法。数值和理论分析结果与实验结果对比，吻合良好，可以为材料的界面性能分析和材料设计提供参考依据。

剪滞理论； cohesive模型； 界面； 单丝段裂； 有限元模拟

1 引 言

纤维增强复合材料因其具备高比强度、高比刚度等特点，应用日益广泛[1]。许多学者从不同角度研究了复合材料的性能。肖颖[2]等从材料宏观结构的角度通过对复合材料层合板等效模量的反演推算，得到了单向板的弹性常数。王唱舟[3]等分析了复合材料微观结构对材料力学性能的影响。由于界面承担了基体和增强相之间的应力传递功能[4]，对复合材料性能影响很大。孙志刚[5]等研究了界面几何结构对复合材料力学性能的影响。除了和基体、增强相材料本身性能有关外，复合材料的性能在很大程度上受细观界面性能的影响[6]。

Cox应用剪滞理论分析了纤维增强复合材料纤维/基体间的应力传递[7]，但没有考虑非理想界面因素的影响，即认为纤维和基体之间是理想粘接的。而实际上，界面一般都存在缺陷。Shetty等在剪滞理论中引入了界面摩擦特性来描述界面的脱粘情况[8]。Chen等利用线性界面准则考虑了界面损伤对复合材料断裂韧性的影响[9]。目前，描述复合材料纤维基体间界面的力学行为主要有三种模型，分别是线性弹簧模型[10]、三相材料模型[11]和内聚力模型(CZM)[12]。其中CZM用牵引力同分离量函数关系曲线表征纤维/基体的界面力学行为，模拟界面硬化、软化直至破坏的过程，在理论和数值模型中被广为应用。Needleman应用CZM研究了金属基复合材料的增强相脱粘[13]。李巾锭[14]等在有限元分析中引入CZM模拟了C/SiC复合材料的纤维顶出过程。CZM的本构关系有多种形式：理想塑性模型[15]、梯形模型[16]和双线性模型[17]等，其中的双线性本构模型应用最为广泛。

由于界面的特殊性，表征界面的CZM参数很难直接获得。在理论和数值分析模型中使用的CZM参数多是根据实验或者半经验的方法来估测[18]。王晓宏等结合电阻实验和单丝段裂实验的方法估测了纤维增强复合材料的界面刚度[19]，该方法只适用于纤维材料为导体的情况。韩庚等建立了单丝段裂有限元模型，从实验和数值模拟的角度讨论了不同组份相参数对于单丝段裂过程的影响[20]，但没有给出理论解释。Bentang等结合单丝段裂实验和有限元模拟，反向估测了界面参数[21]。上述分析界面的模型多采用二维模型，没有考虑三维模型情况。

实验研究方面，张鸿[22]等分析了陶瓷基复合材料的单纤维拔出过程。Kelly和Tyson通过对埋入基体中的单丝纤维进行段裂实验来研究界面的粘接质量[23]。这是目前研究界面应用较为广泛的方法。Beckermann等学者应用该方法得到了植物纤维增强复合材料的界面剪切强度[24]。C. Guillebaud-Bonnafous等利用该实验方法得到大麻纤维增强树脂基复合材料界面强度为21MPa，但利用摩擦模型得到约为15.5MPa[25]，存在一定差异。

本文在经典剪滞模型中，引入双线性cohesive模型表征界面，重新分析了纤维增强复合材料的纤维/基体之间的应力传递机理。用理论分析和有限元模拟结果解释了单丝段裂实验中的实验现象。讨论了不同的分析参数对应力分布结果的影响。建立了利用cohesive单元表征界面的复合材料单丝段裂三维有限元模型。提出了一个估测界面参数的新方法。

2 理论分析

2.1 双线性cohesive模型

双线性CZM是表征纤维基体界面最有效也是最常用的一种模型。本文应用该模型表征纤维基体间的非理想界面的力学行为，其沿界面切向的牵引力-分离关系曲线如图1所示。

图1 双线性内聚力理论模型Fig.1 Theoretical model of bilinear CZM

图1中，OA段为弹性阶段，应力值随着分离量的增加而线性增加，其斜率K即为界面刚度。当应力达到峰值后，进入表示损伤累积的AB阶段，此阶段应力值随着分离量的增加而线性降低，直至应力为0，此后进入完全脱粘的BC段，应力保持为0。本文提出了一个确定K的新方法。

2.2 应力传递分析

图2为应力传递分析的简化模型，模型长度为2L，中点为坐标原点，基体受应变载荷ε0作用。由弹性力学基本方程：平衡方程，物理方程，几何方程，对模型中的纤维和基体分别进行应力分析。

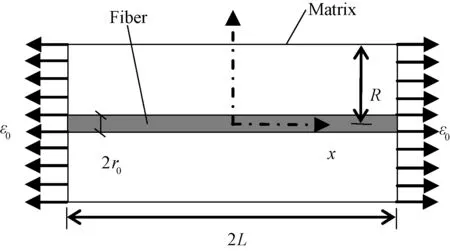
图2 应力传递分析模型Fig.2 Model of transfer analysis for stress

对纤维进行应力分析可以得到：

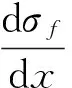
(1)

σf=Efεf

(2)

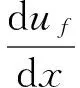
(3)

对基体进行应力分析可以得到：

2πr0τθ=2πrτ

(4)

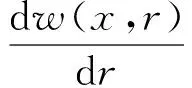
(5)

τ=Gmrm

(6)

其中，τθ为纤维基体界面上的切应力；r0为纤维的半径；σf和εf分别为纤维的轴向应力和轴向应变，二者都是关于x的函数；uf为纤维的轴向位移；rm为基体沿x方向的剪切应变；w(x,r)为x处距纤维中心距离为r处基体的位移；τ(x,r)为距离纤维中心为r处基体沿x方向的剪应力；Gm为基体的剪切弹性模量。利用上述方程和剪滞理论的基本假定，可以得到如下方程。

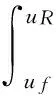
(7)

2.3 引入双线性cohesive模型

在式(7)中，左侧积分下限为纤维基体界面位置，即r=r0处位移。积分上限为基体边界处，即r=R处位移。显然，直接利用式(7)积分得到的是纤维和基体在界面上位移一致时的结果。而由于基体同纤维之间存在相对滑移，所以在界面处基体的位移同纤维的位移是不等的。引入双线性cohesive模型可知，在OA线弹性段滑移量为τθ/K，由式(7)可得到，

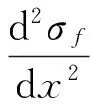
(8)

其中

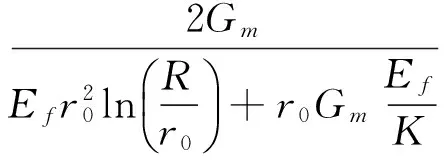
(9)

式(8)的通解为

σf=Efε0+Asinh(nx)+Bcosh(nx)

(10)

引入边界条件，则当x=L和x=-L时，σf=0，可得

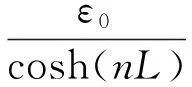
则此时的应力分布为

(11)

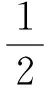
(12)

由式(11)和式(12)可以得出材料的最大拉伸应力在纤维中心，其值为

σmax=Efε0[1-sech(nL)]

(13)

而最大界面切应力发生在纤维两端。

3 理论分析结果与讨论

第2节中得到了不同分析参数同应力分布结果的关系式。为了更直观地讨论这些分析参数对于复合材料应力分布形式及单丝段裂过程的影响，引入文献[25]中的实验相关参数，如表1所示。

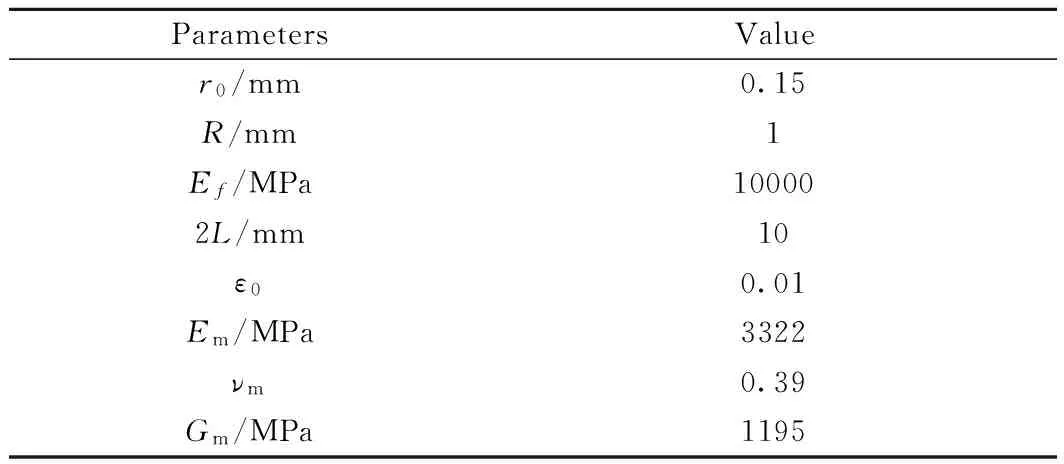
表1 不同分析参数的取值

3.1 纤维弹性模量和基体弹性模量对单丝段裂过程的影响

段裂过程中，认为当纤维的轴向最大正应力σmax达到其极限强度时纤维段裂。在σmax的表达式(13)中分别分析纤维的弹性模量Ef和基体的弹性模量Em对σmax的影响，取不同界面刚度K值，其它参数取值均见表1，得到σmax分别随Ef和Em变化的曲线，如图3和图4所示。

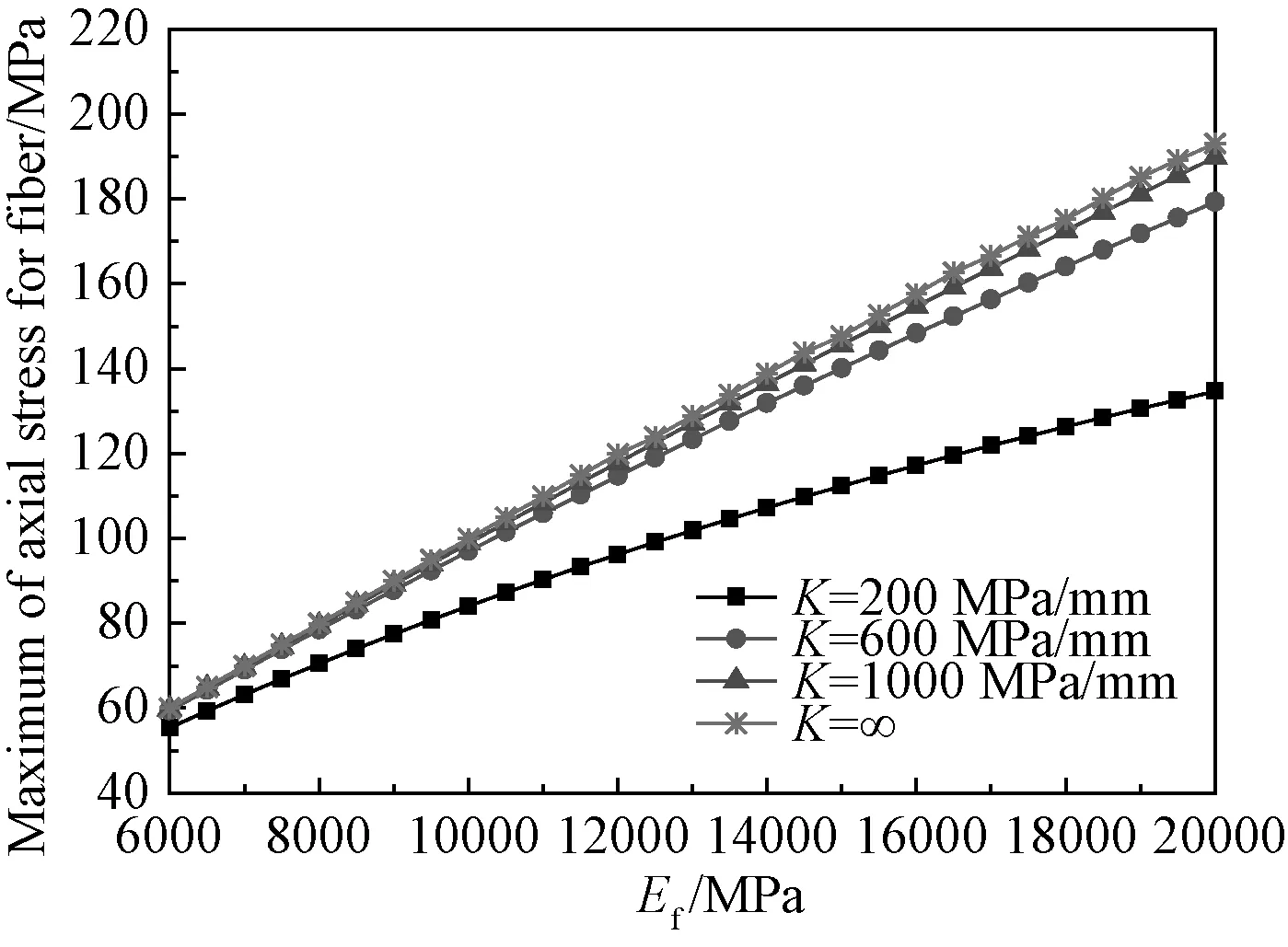
图3 不同界面刚度下纤维轴向应力的最大值随纤维弹性模量的变化曲线Fig.3 Maximum of axial stressfor fiber to modulus of fiber in different stiffness of interface

由图3可知，随着纤维弹性模量Ef的增加，纤维的轴向正应力σmax也增加。即当外加应变载荷相同时，较高的Ef会产生更大的σmax，因此，纤维会较早的段裂。而图4中，随着基体弹性模量Em的增加，虽然σmax有所提高，但变化相对较小，所以Em的变化对纤维的段裂起始时刻影响不大。

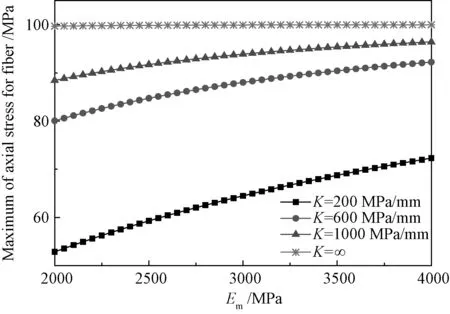
图4 不同界面刚度下纤维的轴向应力随基体弹性模量的变化曲线Fig.4 Maximum of axial stress of fiber to modulus of matrix in different stiffness of interface

对比图3和图4可知，随着界面刚度K的增加，两图中的曲线都趋近于界面理想粘接时的情况(K=∞)。并且，纤维的轴向正应力σmax随纤维弹性模量Ef和基体弹性模量Em的变化也更趋近于线性。但图3中，K值越大σmax随Ef的变化幅度也越大，而图4中K值越大，σmax随Em的变化幅度越小。因此对于K较大的情况，提高Ef可以更有效地提高σmax，而相反情况下，则提高Em，可以更有效地提高σmax。

以上利用引入CZM表征界面因素后的应力传递分析结果，讨论了提高纤维弹性模量Ef和基体弹性模量Em对单丝段裂过程的影响，从理论上对韩庚等在文献[20]中运用有限元模拟和实验的方法分析得到的材料参数对单丝段裂过程的影响做出了解释。文献[20]中的结果如表2所示。

表2 不同材料参数的提高对单丝段裂过程的影响Table 2 Effect of improving different parameters of materialson the single fiber fragmentation

3.2 界面刚度的影响

将沿纤维轴向的位置x视为横轴变量，其它参数按表1，取不同界面刚度K，根据式(11)和式(12)可分别得到纤维的轴向应力σf和界面切应力τθ沿x方向的分布情况。如图5和图6所示。

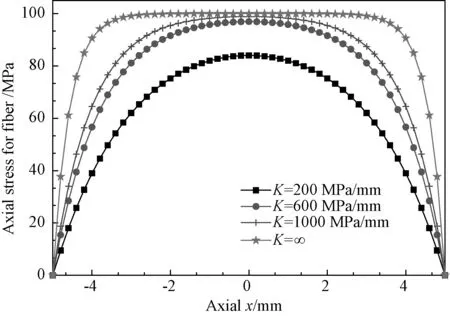
图5 不同界面刚度下纤维的轴向应力分布Fig.5 Distribution of axial stress for fiber in different stiffness of interface

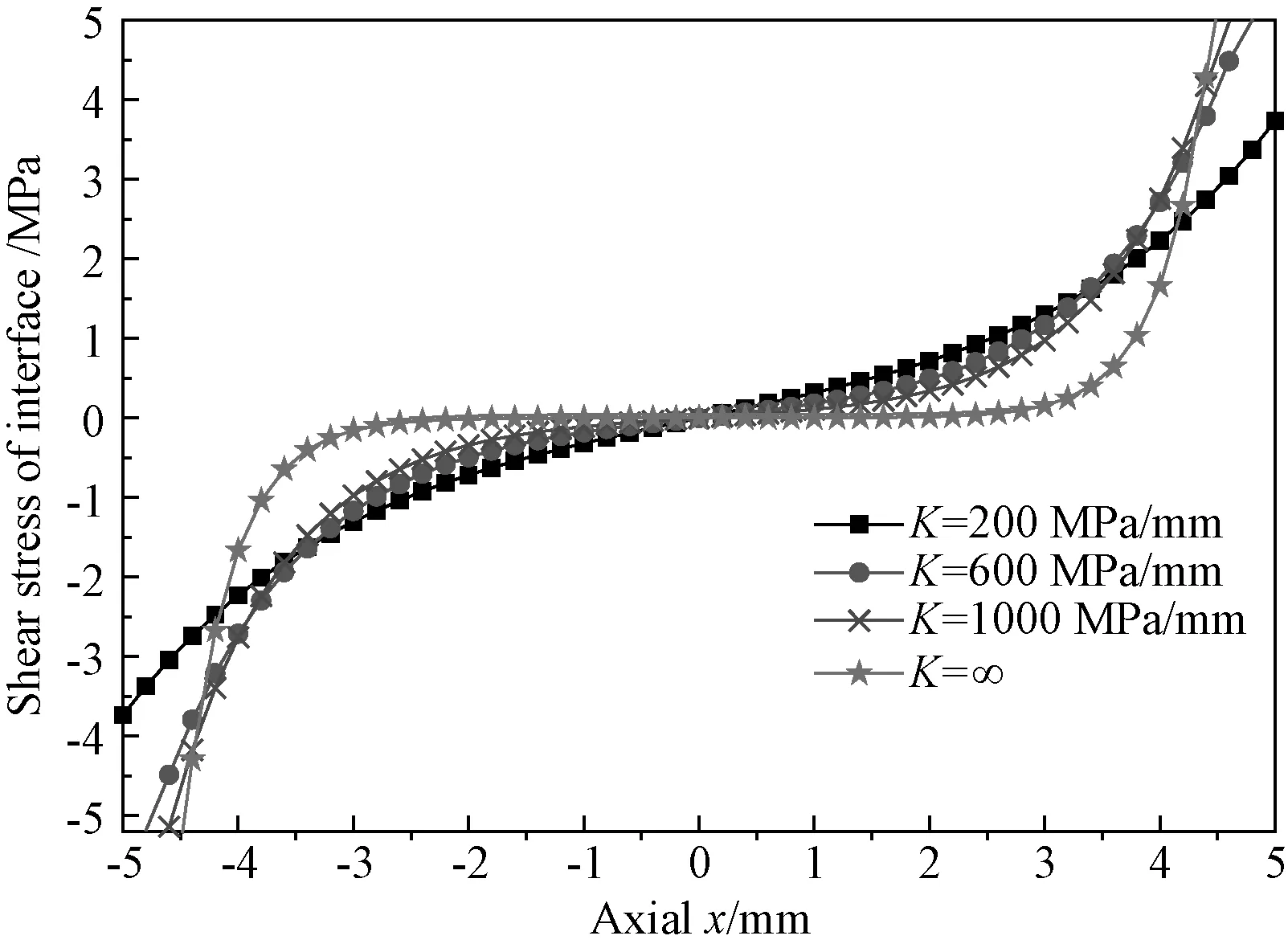
图6 纤维长度较大时不同界面刚度对应的界面切应力的分布图Fig.6 Distribution of interfacial shear stress in different stiffness of interface

图5和图6中，由内到外曲线对应的K值依次增大，最外面一条曲线分别对应K=∞(即纤维基体理想粘接)时的σf分布和τθ分布。显然，从两图中可知，当K值较小时，σf和τθ分布的变化随着K值的变化更为显著，随着K值的增加，其分布渐渐趋于稳定，极限状态就是理想界面时的情况。

由以上的分析可知，在界面刚度K较小时，界面因素对纤维的轴向正应力σf和界面沿纤维轴向的切应力τθ分布影响更明显，即对复合材料的纤维与基体间的应力传递影响越大。所以经典的剪滞理论中，认为纤维和基体之间理想粘接，预测的应力会偏大。

3.3 纤维长度的影响

由式(13)可以看出，纤维轴向正应力的最大值σmax是受纤维长度2L影响的。除纤维长度外，其它参数按表1取值，界面刚度K=1200MP/mm。如图7所示为σmax随纤维长度的变化曲线。

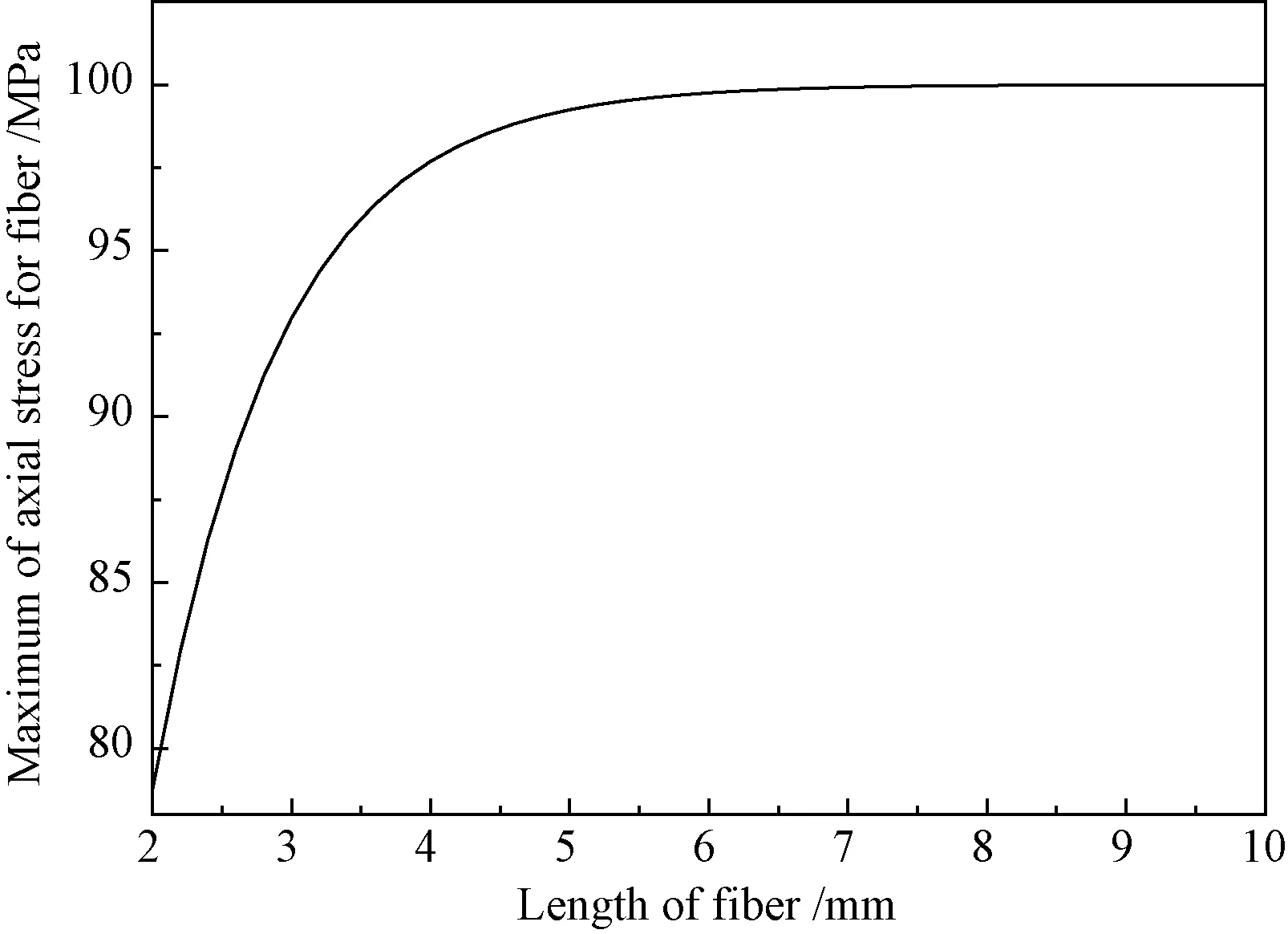
图7 纤维轴向正应力最大值随纤维长度的变化图Fig.7 Maximum of axial stress for fiber to the length of fiber

当纤维长度较短时，如图8所示，得到纤维的轴向正应力分布随界面刚度的变化情况。此时取纤维的长度为2mm，即上述的参量中L=1mm(图4中L=5mm，纤维的长度为10mm，下图同图4相比仅是将参数L变化后的结果)。

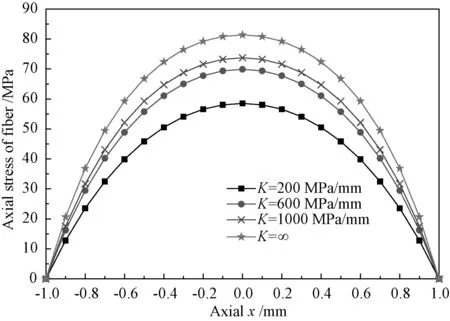
图8 纤维长度较小时纤维轴向正应力分布图Fig.8 Distribution of axial stress for a short fiber in different stiffness of interface

对比图5和图8可知，当纤维的长度越小时，则随着界面刚度的变化整个轴向正应力的分布曲线变化也越明显，即纤维基体界面的应力传递效果，随着纤维的变短，受界面的影响越大。因此纤维长径比越小，界面的影响会越大。图9为当L=1mm时对应的界面上沿纤维轴向的切应力分布图。

图9 纤维长度较小时纤维基体界面切应力的分布图Fig.9 Distribution of interfacial shear stress for a short fiber in different stiffness of interface

对比图9和图6可以发现，当纤维的长度较短时，界面上的切应力在整个界面上沿纤维轴向的变化较为均匀。而当纤维较长时，则界面上的切应力在沿纤维轴向上在中间部分比较平缓，而在靠近边缘部分则迅速增大。所以，当纤维越长则越容易在靠近端部的地方发生界面脱粘。

4 有限元分析

4.1 单丝段裂实验

目前，用于表征界面应力传递的细观力学实验方法主要有：Broutman的纤维拔出实验(Pull-out)[26]、Miler等的微滴脱粘实验(Microdroplet，Microbonding)[27]、Kelly和Tyson的单丝段裂实验(Fragmentation)[23]和Mandell的顶出实验(Push-out，Push-in，Microdebonding)[28]。

单丝段裂实验应用，是研究纤维增强复合材料断裂的重要工具[29]。假设界面的剪切应力为常数，则可以根据著名的Kelly-Tyson常剪应力模型[23]，计算得到界面的剪切强度。本文引用了文献[25]中的实验结果作为对比。

4.2 有限元模拟

引入双线性cohesive模型表征界面，利用有限元软件ABAQUS，建立数值模型，将纤维视为各向同性的线弹性材料，直到断裂。基体是各向同性的线弹性材料。在第二部分的理论推导基础上，结合有关实验和有限元模拟的方法，得到了双线性cohesive模型刚度。该参数可以为分析复合材料的界面性能提供参考。

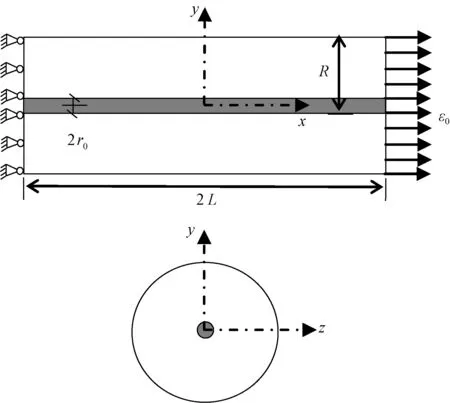
图10 有限元模型二维视图Fig.10 Viewpoint of two-dimension model for FEM

运用ABAQUS脚本语言Python控制CAE建立了三维有限元模拟的几何模型，图10为模型的二维视图。

模型中采用Explicit算法，模型左端固定沿x轴方向位移，右端施加拉伸边界条件，拉伸速度值为0.5mm/min。需要注意的是，边界条件均是施加在基体上的。模型中材料参数如表3所示，其中σb和εb分别表示材料的极限应力和极限应变，其余相关的参数均由表2给出(取自文献[25]中的实验数据)。基体和纤维采用C3D8R单元，界面采用COH3D8单元。

表3 有限元模型中设定的材料参数

4.3 界面刚度的确定

此前得到纤维轴向正应力σf沿x方向的分布为(11)式所示。显然，当材料模型确定后，式(11)只和外加载荷ε0以及n值有关。根据实验结果，可知纤维开始发生段裂时对应的ε0，而此时σf达到极限应力，将该ε0值和σf值代入式(13)中，便可得到对应的n值。

由式(9)可知，此时n和cohesive模型的界面刚度K有关，即cohesive模型中的损伤起始位置δ0和界面完全脱粘位置δf不影响纤维的初始段裂时刻。图11和图12分别为利用有限元分析得到的纤维发生首次段裂时的应变随cohesive模型中的δ0和δf的变化曲线。该结果同理论结果一致。

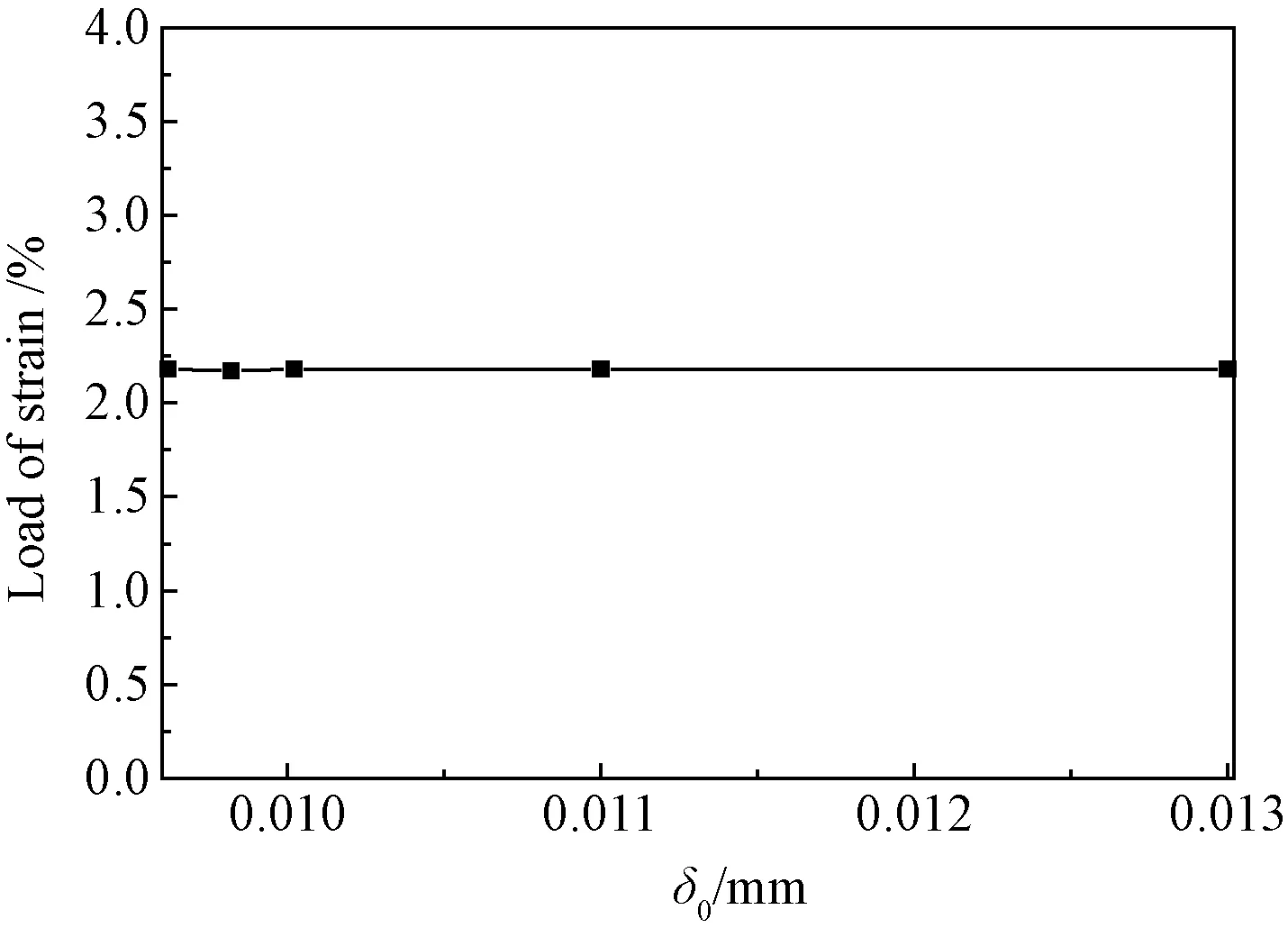
图11 纤维首次断裂时应变载荷随CZM损伤位置的变化曲线图Fig.11 Strain of fiber for initial fracture with different δ0

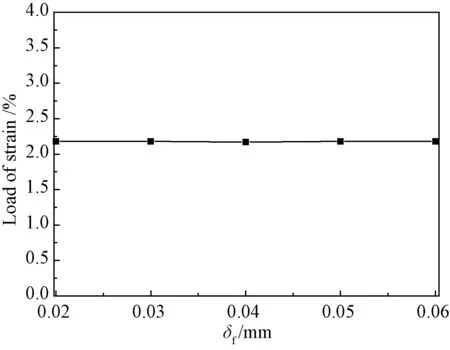
图12 纤维首次断裂时的应变载荷随CZM完全破坏位置的变化曲线图Fig.12 Strain of fiber for initial fracture with different δf

当n值已知时代入式(9)即可得到对应的cohesive界面刚度值K。将表1和表3中的实验中发生首次段裂时对应的外加应变载荷2.1%代入式(13)，得到此时对应的n=1.20729。将该值代入式(9)中得到对应的界面刚度值为K=1855.35MPa/mm。将该界面刚度值作为已知量代入到有限元模型中，有限元分析过程中，外加应变载荷达到2.18%时，纤维发生首次断裂。同实验分析结果吻合。图13为有限元单丝段裂模拟分析结果。这为估测界面刚度性能提供了一种较为简便的方法。

图13 单丝段裂的有限元分析结果剖面图Fig.13 Result of FEM forsingle fiber fragmentation

5 结 论

1.在经典剪滞理论的基础之上，引入双线性cohesive模型表征纤维基体界面，考虑了非理想界面因素对纤维基体间应力传递的影响。得到纤维轴向正应力分布及界面切应力分布结果。

2.利用新的理论分析模型解释了单丝段裂实验中的一些现象。讨论了界面和材料参数对复合材料的应力分布的影响。对界面刚度较大的情况，提高纤维弹性模量可以更有效地提高纤维轴向正应力的峰值，而相反情况下，则提高基体弹性模量，才能更有效地提高纤维轴向正应力的峰值。另外，在界面刚度比较小和纤维较短的情况下，复合材料中的应力分布受界面质量的影响更大，此时不能忽略界面因素的影响。

3.建立了利用cohesive界面单元表征复合材料界面性能的三维单丝段裂有限元模型，模拟了单丝段裂过程。结合理论分析提出了一种估测cohesive模型界面刚度的新方法，同实验结果吻合良好。利用以上分析结果，研究复合材料的界面性能对宏观性能的影响以及材料的设计优化，提供了一定依据。

[1] Joshi SV, Drzal LT, Mohanty AK, Arora S. Are Natural Fiber Composites Environmentally Superior to Glass Fiber Reinforced Composites[J]. Composites Part A: Applied Science and Manufacturing, 2004, 35(3):371～376.

[2] 肖颖, 王佩艳, 董永朋. 复合材料性能反演单向板弹性常数的方法[J]. 材料科学与工程学报, 2015, 33(5):726～729.

[3] 王唱舟, 周丽, 王洋, 丁昊. 数值模拟SiCp/Al复合材料的微观结构对力学性能的影响[J]. 材料科学与工程学报, 2015, 33(1):122～126.

[4] Kim J-K, Mai Y-w. High Strength, High Fracture Toughness Fibre Composites with Interface Control—A Review[J]. Composites Science and Technology, 1991, 41(04):333～378.

[5] 孙志刚, 宋迎东, 高德平. 考虑界面时细观几何结构对复合材料力学性能的影响[J]. 材料科学与工程学报, 2004, 22(4): 488～494.

[6] Sager RJ, Klein PJ, Lagoudas DC, et al. Effect of Carbon Nanotubes on the Interfacial Shear Strength of T650 Carbon Fiber in an Epoxy Matrix[J]. Composites Science and Technology, 2009, 69(7-8):898～904.

[7] 杜善义, 王彪. 复合材料细观力学[M]. 北京: 科学出版社, 1997: 6～58.

[8] Shetty DK. Shear-Lag Analysis of Fiber Push-out (Indentation) Tests for Estimating Interfacial Friction Stressin Ceramic-matrix Composite[J]. Journal of the American Ceramic Society, 1988, 71(2):107～119.

[9] Chen YL, Liu B, He XQ, Huang Y, Hwang KC. Failure Analysis and the Optimal Toughness Design of Carbon Nanotube-reinforced Composites[J]. Composites Science and Technology, 2010, 70(9):1360～1367.

[10] Chen W, Zhu X, Huang Z. Modeling of Multi-Inclusion Composites with Interfacial Imperfections: Micromechanical and Numerical Simulations[J]. Science China Technological Sciences, 2010, 53(3):720～730.

[11] Wang HW, Zhou HW, Peng RD, Mishnaevsky L. Nanoreinforced Polymer Composites: 3D FEM Modeling with Effective Interface Concept[J]. Composites Science and Technology, 2011, 71(7):980～988.

[12] Shen M, Xu R, Yuan H. Numerical Simulation of Tensile Behaviors for Random Spruce Short Fiber Reinforced Composites[J].Advanced Materials Research, 2012,487(6): 544～547.

[13] Needleman A. A Continuum Model for Void Nucleation by Inclusion Debonding[J]. Journal of Applied Mechanics, 1987, 54(3):525～531.

[14] 李巾锭, 任成祖, 张立峰, 吕哲. C/Sic复合材料纤维顶出有限元分析[J]. 材料科学与工程学报, 2014, 32(2):248～254.

[15] Dugdale DS. Yielding of Steel Sheets Containing Slits[J]. Journal of the Mechanics and Physics of Solids, 1960, 8(2): 100～104.

[16] Tvergaard V, Hutchinson JW. The Relation Between Crack Growth Resistance and Fracture Process Parameters in Elastic-plastic Solids[J]. Journal of the Mechanics and Physics of Solids, 1992, 40(6):1377～1397.

[17] Geubelle PH, Baylor JS. Impact-Induced Delamination of Composites: a 2D Simulation[J]. Composites Part B: Engineering, 1998, 29(5):589～602.

[18] Chandra N, Li H, Shet C, Ghonem H. Some Issues in the Application of Cohesive Zone Models for Metal-Ceramic Interfaces[J]. International Journal of Solids and Structures, 2002, 39(10):2827～2855.

[19] Liu C, Zhou Z, Wang X, Zhang B. Analysis and Determination for the Parameters of “Cohesive Element” in the Numerical Model of Single Fiber Composites: the Elastic Parameters[J]. Journal of Reinforced Plastics and Composites, 2012, 31(17):1127～1135.

[20] 韩庚, 关志东, 杜善义, 李星, 何为. 单丝复合体系渐进损伤过程模拟及组分性能对损伤过程的影响[J]. 复合材料学报, 2014, 31(4):1053～1062.

[21] Budiman BA, Takahashi K, et al. A New Method of Evaluating Interfacial Properties of A Fiber/Matrix Composite[J]. Journal of Composite Materials, 2015, 49(4):465～475.

[22] 张鸿, 宋迎东. 陶瓷基复合材料单纤维拔出过程分析[J]. 材料科学与工程学报, 2008, 26(6):837～842.

[23] Kelly A, Tyson WR. Tensile Properties of Fibre-reinforced Metals: Copper/Tungsten and Copper/Molybdenum[J]. Journal of the Mechanics and Physics of Solids, 1965, 13(6):329～350.

[24] Beckermann GW, Pickering KL. Engineering and Evaluation of Hemp Fibre Reinforced Polypropylene Composites: Fibre Treatment and Matrix Modification[J]. Composites Part A: Applied Science and Manufacturing, 2008, 39(6):979～988.

[25] Guillebaud-Bonnafous C, Vasconcellos D, et al. Experimental and Numerical Investigation of the Interface Between Epoxy Matrix and Hemp Yarn[J]. Composites Part A: Applied Science and Manufacturing, 2012, 43(11):2046～2058.

[26] Broutmari L. Measurement of the Fiber-Polymer Matrix Interfacial Strength[J]. Interfaces in Composites, 1969, 45(2): 1027～1039.

[27] Miller B, Muri P, Rebenfeld L. A Microbond Method for Determination of the Shear Strength of a Fiber/Resin Interface[J]. Composites Science and Technology, 1987, 28(1): 17～32.

[28] Mandell JF, Chen JH, Mcgarry FJ. A Microdebonding Test for in Situ Assessment of Fibre/Matrix Bond Strength in Composite Materials[J]. International Journal of Adhesion And Adhesives, 1980, 1(1):40～44.

[29] Liu C, Wang X, Wang Y. Analysis on the Process of Stress Transferring in Single Fiber Composite and Monte-carlo Simulation on the Process of Single-Fiber Fragmentation[J]. Journal of Reinforced Plastics and Composites, 2014, 33(12): 1105～1119.

Re-analysisofInterfaceStressTransfersandParameterEvaluationforCohesiveZoneModel

WANGKansheng,SHENMin,YUJisong

(Departmentofmechanics,Schoolofmechanicalengineering,TianjinUniversity,Tianjin300072,China)

Based on the classical shear lag model, the bilinear cohesive zone model (CZM) was introduced by taking imperfect interfacial factors into consideration to reanalyze the interface stress transfer mechanism of fiber-reinforced composite materials. New stress distribution results of the fiber reinforced composite materials are obtained. Some phenomena that occurred in single fiber fragmentation experiments can be explained by these results. Effect of different interfacial parameters and material properties on the result of stress distribution was discussed. Based on the theoretical analysis, interface of cohesive element was introduced to establish a three dimensional finite element model that simulated the single fiber fragmentation experiment. Thereafter, a new method of estimating interfacial CZM parameter was put forward combining with experimental result of single fiber fragmentation. Theoretical analysis results and the FEM results are in good agreement with the result of experiment. Some support can be provided for research of interfacial properties and design of composite by these results.

shear-lag model; cohesive zone model; stiffness of interface; single fiber fragmentation; finite element method

2016-03-21；

2016-05-20

国家自然科学基金资助项目(10972155，11572218，81670884)

王坎盛(1990-)男，硕士研究生，主要研究方向为复合材料力学。E-mail：wangkansheng1991@sina.com。

沈 珉(1963-)男，副教授，博士，主要研究方向为复合材料材料力学。E-mail：minshen@tju.edu.cn。

1673-2812(2017)06-0945-07

TB332

A

10.14136/j.cnki.issn1673-2812.2017.06.017