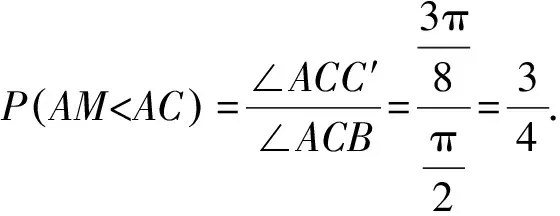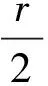中学数学概率教学中两个“多方法”问题的困惑

刘国海

(海南省农垦中学 570226)

概率与统计问题与我们的日常生活密切相关，是理论联系实际的重要体现．同时，中学数学中的概率与统计又是大学《概率论及数理统计》的重要基础．因此，在往年的各地高考和模拟考试中经常出现一些概率问题，其善变、新颖的情境总是给人眼前一亮、耳目一新的感觉.

笔者在概率教学过程中，发现两个问题，学生解决时容易产生几种不同的解法．但每种解法得到的结果未必相同，也就是出现“一题多解”的困惑.

问题一：几何概型

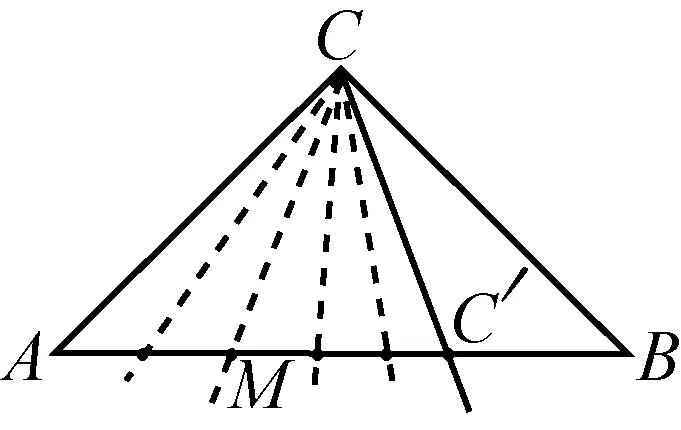
例1在等腰Rt△ABC中，在斜边AB上取一点M，求AM

解法一：如图1，在AB上截取AC′=AC，于是

图1

图2

其实以上两种解法是我们的学生在解题过程中常出现的不同结果，似乎各有各的道理，孰是孰非，这是我们值得深思的一个问题.

在概率论发展的初期阶段，人们就发现不能仅仅考虑随机现象的可能结果只有有穷个基本事件，还要研究“无穷个基本事件”的情形.

假设某一随机现象的样本空间，可用欧氏空间的某一区域S表示，其样本点具有所谓“均匀分布”的性质．在我们解决这类问题时，总是假设区域S以及其中任一可能出现的小区域A都是可以度量的，其度量大小用μ(A)表示(如一维长度，二维面积，三维体积).

回过头看例1，解法一考虑的是长度之比，解法二考虑的是角度，也可以理解为两个半径无穷大的扇形面积之比．其实两种解法是对研究对象的理解偏差导致的．而针对本题，笔者认为解法一是切合题意的，因为这里考察的是点M的位置．如果把题目变为：在等腰Rt△ABC中，在∠ACB内部，以C为起点任作一条射线，交斜边AB于点M，求AM

再如：

例2如图3，A,B两盏路灯之间长度是30米，由于光线较暗，想在其间再随意安装两盏路灯C、D，问A与C，B与D之间的距离都不小于10米的概率是多少？

图3

解法一：记

E

：“

A

与

C

，

B

与

D

之间的距离都不小于10米”．把

AB

三等分，由于中间长度为

米，所以

图4

类似例1、例2这类题目所谓的“多解”可能是“伪解”，很可能解题方法的切入点就是错误的．也恰恰说明解题要认真分析、审清题意，搞准问题研究的对象，真正理解相关概念的本质，采用最切合题意的解题方法才能得到正确的答案．但也有一类概率问题的“一题多解”是难以辨别孰是孰非的.

图5

图6

图7

问题二：离散型随机变量的分布列

例4从某学校随机抽取16名学生，经校医检查得到每位学生的视力，其中“好视力”4人，以这16人的样本数据来估计整个学校的整体数据，若从中任选3人，记X表示抽到 “好视力”学生的人数，求X的分布列及数学期望.

解法一：依题意，ξ=0,1,2,3，则

所以X的分布列为

X0123P112833709701140

所以X的分布列为

X0123P27642764964164

以上两种解法：一种是超几何分布，一种是二项分布．虽然求出的分布列不同，但最终得到的数学期望是一样的，是“纯属巧合”，还是“必然结果”？其实超几何分布和二项分布是有密切联系的，都属于离散型随机变量分布，但也有一定的区别.

从表象来看，两种分布列的概率求解有完全不同的表达式，但概率分布列构造上又有相似点．高中数学教材中超几何分布的定义是：

设有N件产品，其中M件是不合格品，无放回地任意取n件，则其中恰好有不合格品的件数X服从超几何分布，记作X～H(N,n,M).

由此可见，这两种分布的主要区别就是抽取方式的“有放回”和“无放回”.

这类问题，学生解题时真正区别起来还是有难度的．笔者认为具体甄别应该仅仅抓住超几何分布和二项分布的定义，紧扣“放回”与“不放回”进行判定．针对本例，显然解法一是切题的.

如例4变为：若从该校(人数很多)任选3人，记X表示抽到 “好视力”学生的人数，求X的分布列及数学期望．那么这个问题用二项分布(解法二)就更切题了，这一点我们可以认真体会一下.

概率统计主要探讨现实生活中的数据和随机现象，并且通过对数据收集、整理、分析帮助人们作出合理的决策．由于概率统计纳入中学数学课程的时间不是很长，致使概率的教学研究相对不够成熟，学生们在学习这一部分知识时还存在一定的困难．因而，让学生理解它的内容与思想方法，培养学生良好的直觉，让学生的思考在分析真实数据中形成，让学生的理解在集体讨论中加深，尤其是对一些概念的讨论和辨析至关重要．