基于JFO空化和幂律模型的螺旋槽液膜密封流体动压特性

王赟磊，郝木明，李振涛，李勇凡，孙鑫晖，徐鲁帅

（中国石油大学（华东）密封技术研究所，山东 青岛 266580）

基于JFO空化和幂律模型的螺旋槽液膜密封流体动压特性

王赟磊，郝木明，李振涛，李勇凡，孙鑫晖，徐鲁帅

（中国石油大学（华东）密封技术研究所，山东 青岛 266580）

密封端面间润滑流体的非牛顿特性对密封的性能有重要影响。基于满足质量守恒的JFO空化边界条件及描述流体非牛顿特性的幂律模型，建立了考虑流体非牛顿特性的螺旋槽液膜密封数学模型。采用有限差分法对控制方程进行离散，通过SOR迭代方法对离散方程进行求解，得到了密封端面液膜压力分布。探讨了润滑流体的非牛顿特性对螺旋槽液膜密封的液膜承载能力、泄漏量、摩擦扭矩等性能参数及液膜中空化发生情况的影响规律。结果表明：随着幂律指数的增大，液膜承载能力先增大后减小，泄漏量和空化率增大，摩擦扭矩减小；幂律指数为0.96时，相对于牛顿流体，液膜承载能力提升约4.6%，密封端面空化率下降约98.6%，泄漏量下降约5.8%，摩擦扭矩增加约0.3%；随着操作参数的改变，不同幂律指数下的流体动压性能参数变化规律具有相似性；润滑流体的合理选择对液膜密封性能改善有重要意义。

螺旋槽液膜密封；幂律模型；非牛顿流体；JFO边界条件；流体动压特性

引 言

螺旋槽液膜润滑非接触式机械密封（简称液膜密封）因其可实现被密封介质的零泄漏甚至零逸出，消除泄漏物对环境的污染，在工业上得到了广泛应用[1-2]，胶乳泵和高温热油泵采用下游泵送液膜密封；丁二烯螺杆压缩机采用人字槽和八字槽液膜密封，人字槽和Y形槽液膜密封同时具有上游泵送和下游泵送功能[3]。在对液膜密封的理论分析当中，多采用牛顿流体假设[4-6]。而实际上，工业上采用的润滑油多是在基础油的基础上添加高分子聚合物而成，用以改善润滑油的性能，这些聚合物的添加使润滑油呈现出非牛顿性质，流体的剪应力与剪应变率呈非线性关系。此外，当润滑油中含有少量的气体（如空气、气泡等）时，润滑油的流变行为也将明显偏离牛顿流体[7-8]。这些使得润滑油的非牛顿流变特性成为密封设计中不可忽视的因素，采用牛顿流体假设去解决液膜密封问题，结果会存在一定的偏差。针对润滑油的非牛顿流变特性，相关研究者提出了幂律模型（power law）[9-10]、偶应力流体模型（couple stress）[11]、微极性流体模型（micropolar）[12]以及赫谢尔-巴克利模型（Herschel-Bulkey）[13]。在上述这些模型当中，幂律模型方程参数少且能够准确描述流体的剪切稀化或稠化特性，在工程中得到了广泛的应用[14]。

螺旋槽液膜密封在工作过程中，在螺旋槽几何发散区会出现负压现象，由于液膜不能承受负压强，在负压的作用下液膜不能保持连续而产生空化。空化现象对机械密封端面间液膜压力的分布、液膜承载能力及密封稳定性具有较大影响[15-17]。在进行液膜密封性能研究时，应考虑空化现象。目前常用的空化边界条件主要有两种：Reynolds边界和JFO边界（质量守恒边界）[18-19]。Reynolds边界通过负压充零算法来实现，实验表明该边界条件可准确预测液膜破裂位置，但是无法正确描述液膜再形成区域，且不符合质量守恒定律。而JFO边界可以同时捕捉液膜的破裂和重生成区域，是较为符合实际的空化边界条件[20-22]。针对JFO边界的数值实现，Elrod[23]提出空化算法将描述全液膜区和空化区的方程统一为一通用方程。Brewe[24]和 Vijayaraghavan等[25]对Elrod算法进行了改进。Fesanghary等[26]针对Elrod算法，提出了一种改进的开关函数，使Elrod算法的稳定性和收敛速度得到提高。目前，针对液膜密封流体动压特性研究，大多已经考虑了空化对密封性能的影响[27-29]，但尚未综合考虑空化和润滑流体非牛顿特性对螺旋槽液膜密封流体动压封性能的影响。

为使理论模型更加准确地预测液膜密封的性能，在现有的理论模型基础上考虑润滑流体的非牛顿流变特性。本文结合雷诺方程和幂律模型，同时考虑满足质量守恒的JFO空化边界条件，探究润滑油的非牛顿特性对下游泵送螺旋槽液膜密封的液膜承载能力、泄漏量、摩擦扭矩等流体动压性能参数以及液膜中空化发生情况（空化率）的影响，为完善液膜润滑及密封机理提供可靠依据，同时为后续进一步开展及优化设计人字槽和Y形槽等典型液膜密封提供实验参数和理论指导。

1 理论模型

1.1 几何模型

图1示出了螺旋槽液膜密封端面结构，动环表面开设有螺旋槽，动环做旋转运动时，摩擦副间处于全液膜润滑状态。图1中：ri和ro分别为密封环内、外半径；rgi和rgo分别为螺旋槽的内槽根半径和外槽根半径；θc为单周期计算区域的周期角；θL和θG分别为单个台区和槽区的圆周角；α为螺旋角；pi和po分别为内、外径处压力。

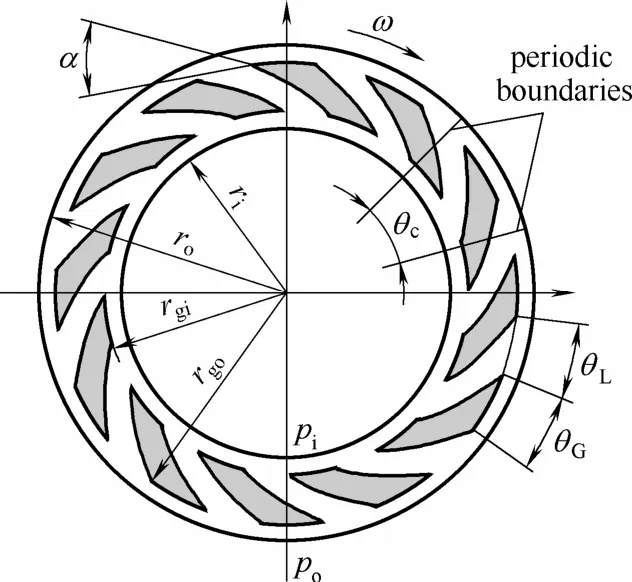
图1 密封端面结构Fig.1 Structure of sealing face

1.2 数学模型

螺旋槽液膜密封端面间液膜厚度远远小于其他方向的尺寸，为对N-S方程进行简化，可进行如下假设[30-31]：（1）忽略体积力和惯性力的影响；（2）流体在固体界面上无滑动；（3）液膜表面的曲率半径相对于液膜厚度很大，故忽略曲率对液膜流场的影响，做出简化，利用平动代替转动；（4）不计沿膜厚方向的压力梯度；（5）流体的流动为层流；（6）忽略除u、v方向外其他速度梯度。密封间隙示意图如图2所示，图中，hg为槽深；h0为非槽区液膜厚度；在槽区，膜厚为hg+h0。

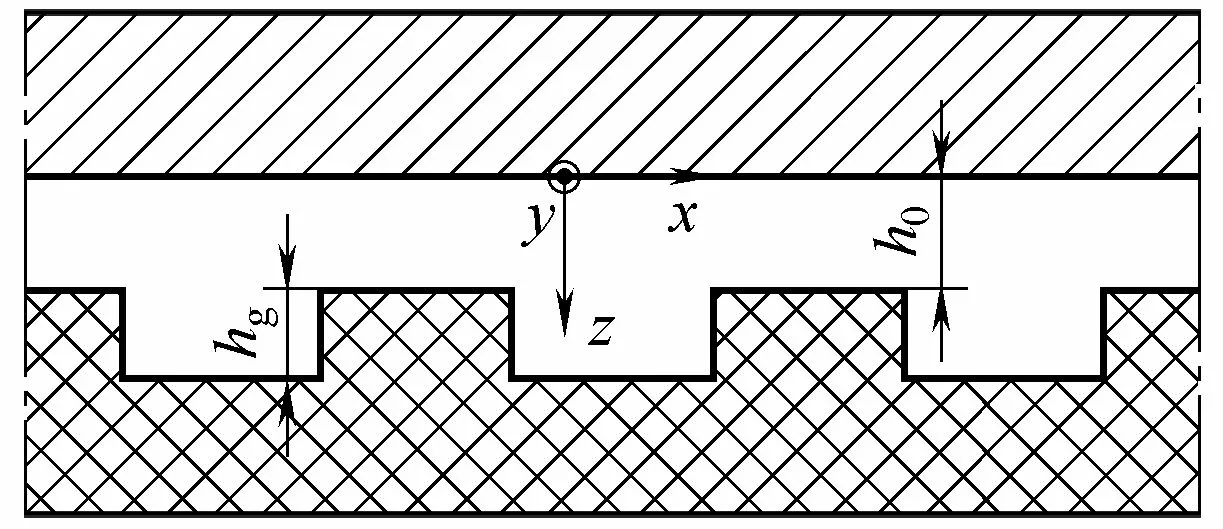
图2 密封间隙示意图Fig.2 Schematic diagram of sealing clearance

基于上述假设，简化N-S方程得

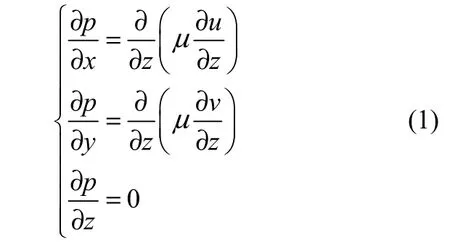
速度边界条件为

对式(1)沿z方向积分，代入边界条件后得

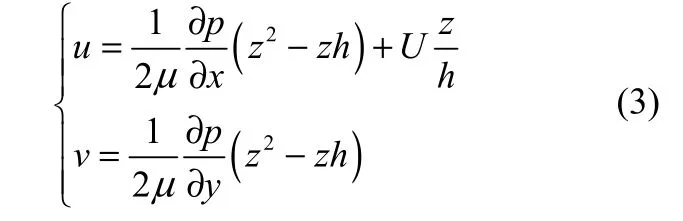
幂律模型可表述如下[32]

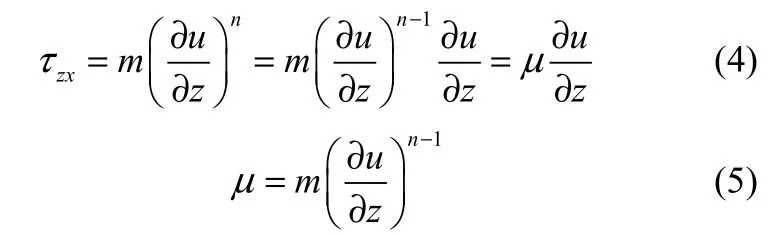
结合可压缩流体定常流动连续性方程

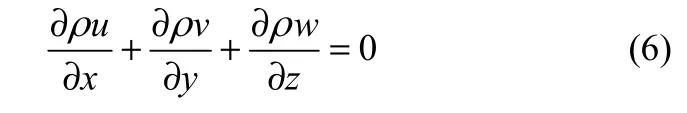
对连续性方程沿z方向积分，可得方程为

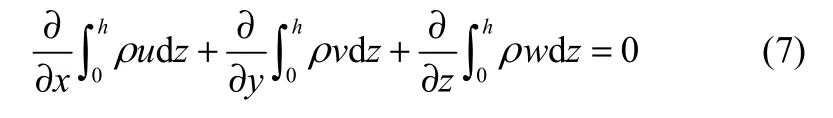
将式(3)和式(5)代入式(7)，得

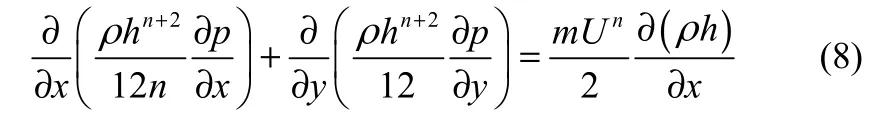
式中，n为幂律指数，m为稠度系数。当n＜1时，流体具有剪切稀化特性；当n＞1时，流体具有剪切稠化特性；当n=1时，式(8)即为描述牛顿流体的雷诺方程。将式(8)转化为极坐标形式为

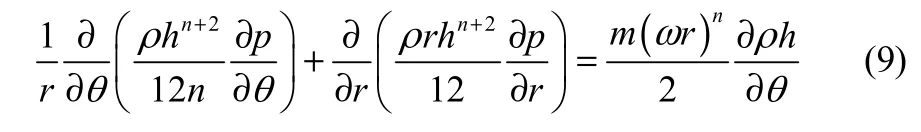
螺旋槽液膜密封在工作中，由于几何发散区的存在，会出现局部压力低于润滑液体饱和蒸气压的情况，从而产生空化。为了在求解过程中同时捕捉液膜的破裂和重生成区域，并且满足基于质量守恒的JFO空化边界条件，引入通用变量φ和开关函数g，其中

相应地，液膜压力可表示为

将式(10)～式(12)代入式(9)，可得到适用于幂律型非牛顿流体的广义雷诺方程

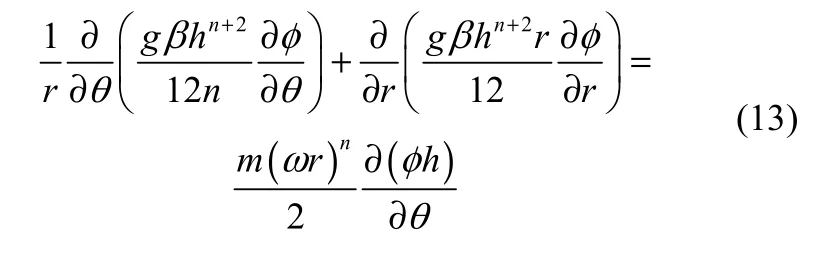
2 数值计算方法

2.1 控制方程离散求解

式(13)采用有限差分方法进行离散，计算区域内的网格划分如图3所示：p为中心节点，n、s、w、e分别代表与中心节点p相邻的4个节点。沿着s→n方向，步长为Δr，沿着w→e方向，步长为 Δθ。

对式(13)离散，整理后可得式(14)

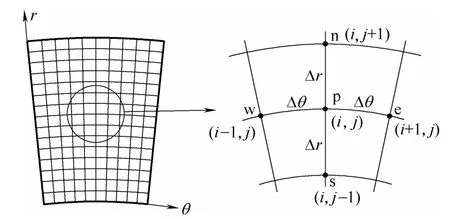
图3 计算网格划分Fig.3 Grid for computation

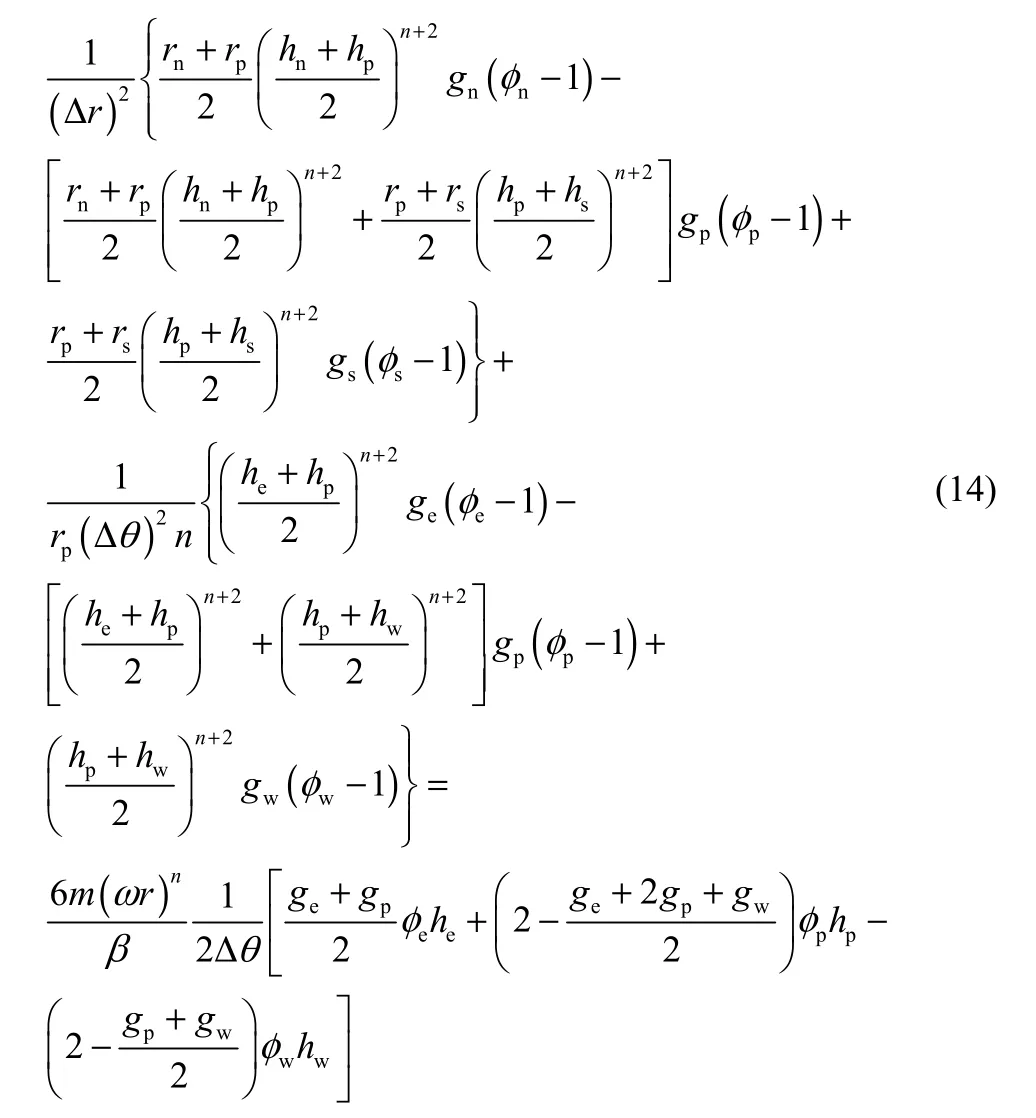
对式(14)进行整理，中心节点p处的φ值表达式为

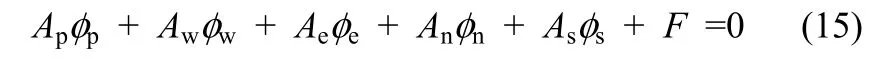
式中的各系数如下

对于式（15），常用的迭代方法有SOR、SLOR、ADI以及多重网格法，本文采用SOR迭代方法对式(15)进行迭代求解。迭代收敛准则为

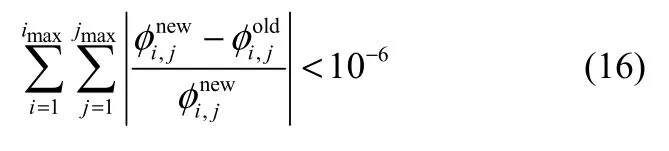
2.2 性能参数

迭代收敛后，可得到通用变量φ和开关函数g在计算区域内的分布，进而可以得到膜压分布及液膜密封流体动压性能参数。

液膜承载能力

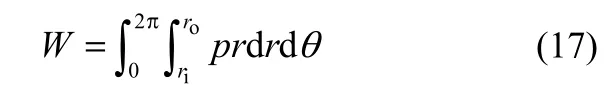
摩擦扭矩

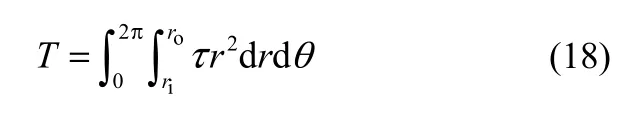
式中

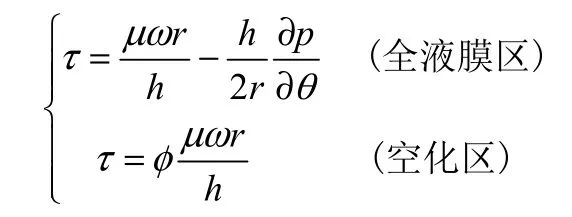
体积泄漏量

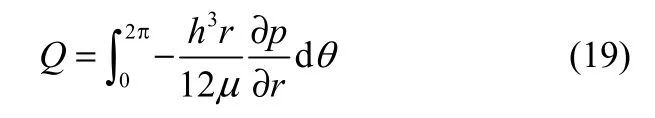
空化率

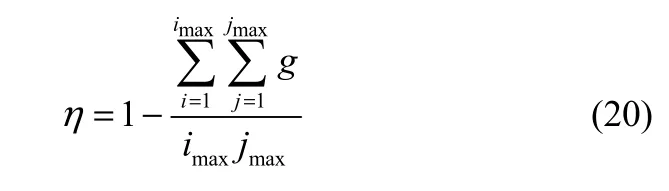
3 计算结果与分析

本文试验和计算分析所采用的螺旋槽液膜密封结构几何参数和工况参数如表1所示。

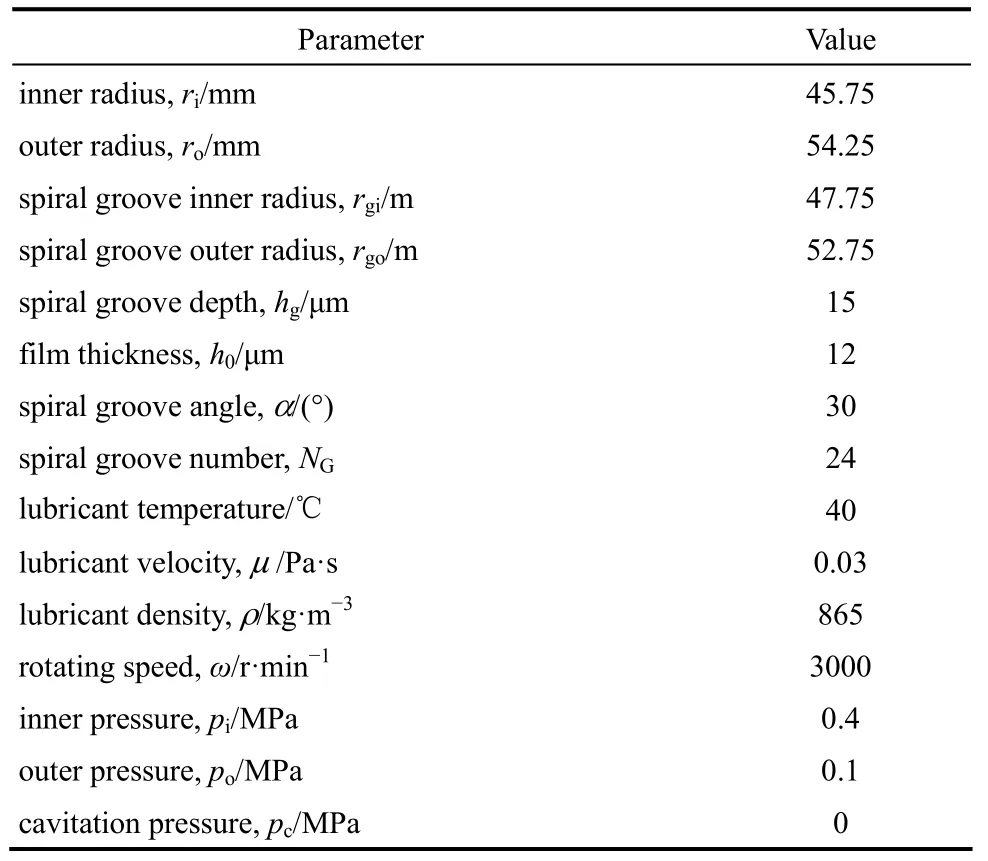
表1 密封面几何结构与工况参数Table 1 Geometrical and operational parameters of sealing surfaces

3.1 数值计算方法验证

为验证数值计算方法的准确性，针对 32#液压油进行了泄漏量试验。图4（a）所示是试验测量所用密封环，图4（b）是密封试验装置，图4（c）是数字式黏度计。

图4 密封环和试验装置Fig.4 Sealing ring and test rig

采用数字式黏度计（DV-1+PRO）对32#液压油进行流变学试验，得到液压油在不同剪切速率下的剪切应力。通过MATLAB中的fittype函数拟合得到幂律指数n=0.9917。图5所示是不同转速下密封端面泄漏量理论计算值与实测值的对比结果。由图可知：计算结果与实测结果存在一定的误差，但整体趋势保持一致，验证了本文数值计算方法的准确性，可开展后续计算工作。

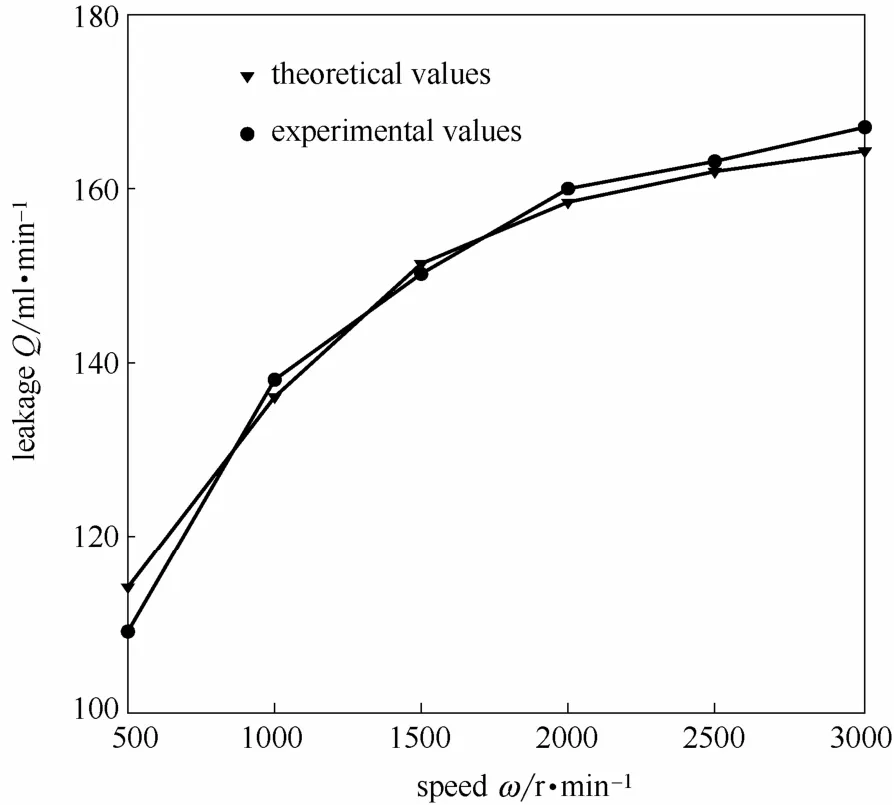
图5 理论计算值与泄漏量实测值对比Fig.5 Comparison between theoretical and experimental values of leakage

3.2 幂律指数对性能参数的影响

为探究幂律指数n对液膜密封流体动压性能参数的影响，针对pi=0.4 MPa，po=0.1 MPa，ω=1500 r·min-1的工况进行研究。

3.2.1 对承载能力和空化率的影响 图6所示为幂律指数n对液膜承载能力和密封端面空化率的影响规律。

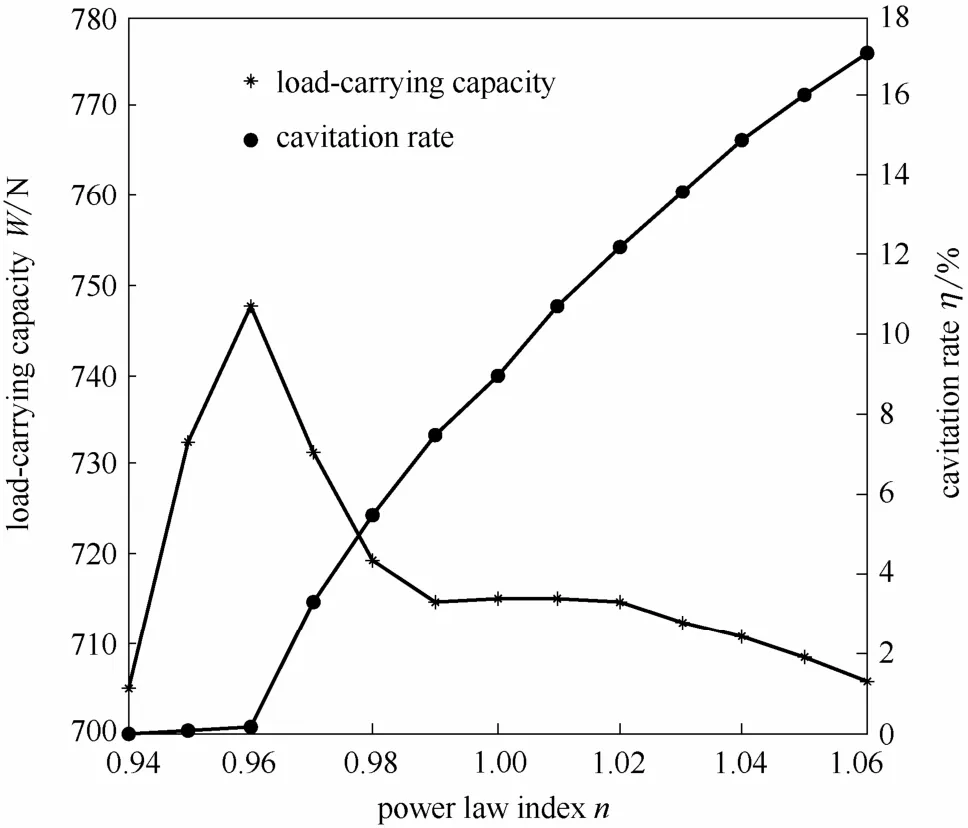
图6 幂律指数对承载能力和空化率的影响Fig.6 Influence of power law index on load-carrying capacity and cavitation rate

由图6可知：当n＞1时，随着n值的增大，空化率近似线性增加，而液膜承载能力呈现下降趋势。n＞1，流体具有剪切稠化特性，黏度增加，动压效应增强提升了液膜承载能力，但空化率的增加使液膜承载能力下降，两相抵消，最终使液膜承载能力呈缓慢下降趋势。

当n＜1时，随着n值的减小，空化率快速下降至零，液膜承载能力先增加后减小，出现最大值，这同样是流体非牛顿特性和空化对液膜承载能力综合作用的结果。n＜1，流体具有剪切稀化特性，黏度减小，动压效应减弱使液膜承载能力下降，但空化率减小对液膜承载能力的提升超过了黏度降低对承载能力的影响，液膜承载能力在这个范围内得到提升。

当n＜0.96时，空化几乎不再发生，其对液膜承载能力的影响可以忽略，此时流体的剪切稀化特性对承载能力的影响得以凸显，随着n值的减小，液膜承载能力快速下降。

n=0.96时，液膜承载能力最大，同时空化减弱明显，相比于n=1的牛顿流体，液膜承载能力提升约4.6%，空化率下降约98.6%。

3.2.2 对摩擦扭矩和泄漏量的影响 图7所示为幂律指数n对摩擦扭矩和泄漏量的影响规律。由图7可知：随着n值的增大，泄漏量增大，而端面摩擦扭矩减小，这是由于n值的改变会影响密封端面压力的分布状况，进而对液膜密封流体动压性能参数产生影响。

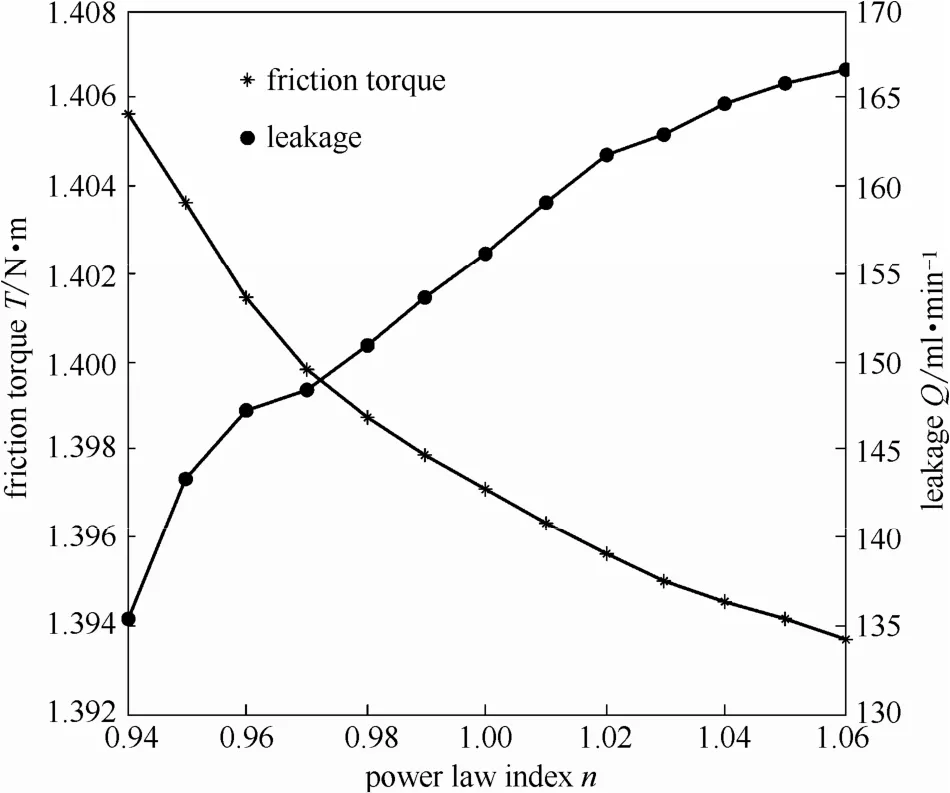
图7 幂律指数对摩擦扭矩和泄漏量的影响Fig.7 Influence of power law index on friction torque and leakage

由图8和图9可知：n值对密封端面的压力分布有显著影响，随着n值的增加，流体的剪切稀化特性减弱，剪切稠化特性增强，黏度的增加造成流体动压效应的增强，使压力分布整体增加，压力分布的形状具有相似性，其最高压力所处的位置也大致不变。随着n值的增大，周向的正压和负压压力梯度均增大，同时空化率也随之增大，由于空化区的周向压力梯度为零（图8），造成摩擦扭矩的减小，但影响程度很小，n=1.06的摩擦扭矩相比于n=0.94的摩擦扭矩，降幅约0.8%；密封端面的径向压力梯度增大（图9），造成泄漏量增大，泄漏量增幅明显，n=1.06的泄漏量相比于n=0.94的泄漏量，增幅约23.1%。相比于n=1的牛顿流体，n=0.96时，泄漏量下降约5.8%，摩擦扭矩增加约0.3%。

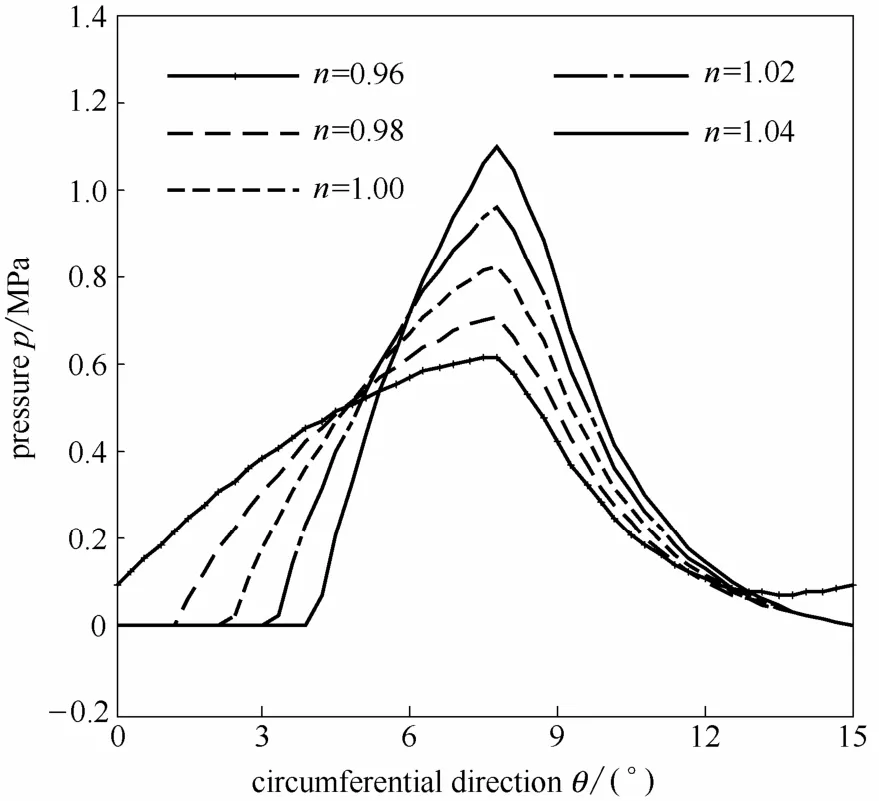
图8 r=51.8 mm处周向压力分布Fig.8 Pressure circumferential distribution at r=51.8 mm

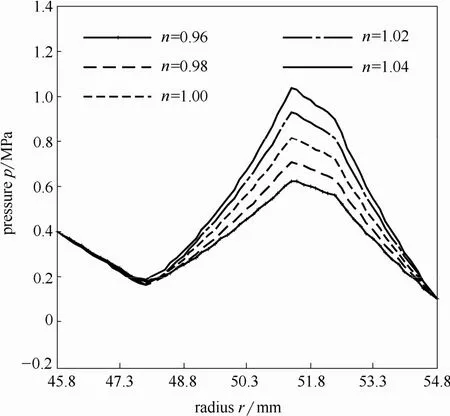
图9 径向压力分布Fig.9 Pressure radial distribution

3.3 转速对性能参数的影响

为探究转速对液膜密封流体动压性能的影响，本文计算了不同转速下的性能参数，转速ω的变化范围为 500～3000 r·min-1。

3.3.1 对承载能力和空化率的影响 图 10所示为液膜承载能力随转速的变化规律。由图可知：随着转速的增大，液膜承载能力呈现先增大后减小并逐渐趋于平稳的趋势。不同n值下的承载能力随转速的变化规律具有相似性。

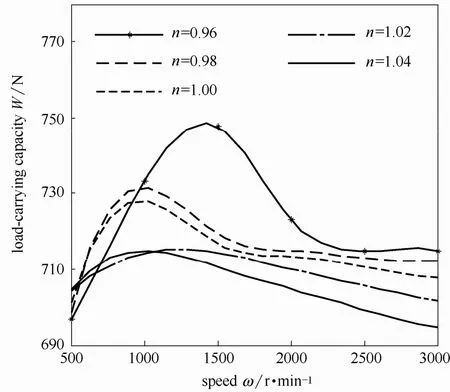
图10 转速对承载能力的影响Fig.10 Influence of speed on load-carrying capacity

由图11可知：随着转速增大，空化率增大。这是由于转速越高，流体的动压效应越强，相应地在膜厚增大的槽区边界处负压效应也越强，此处的液膜压力容易达到空化压力，从而产生空化。

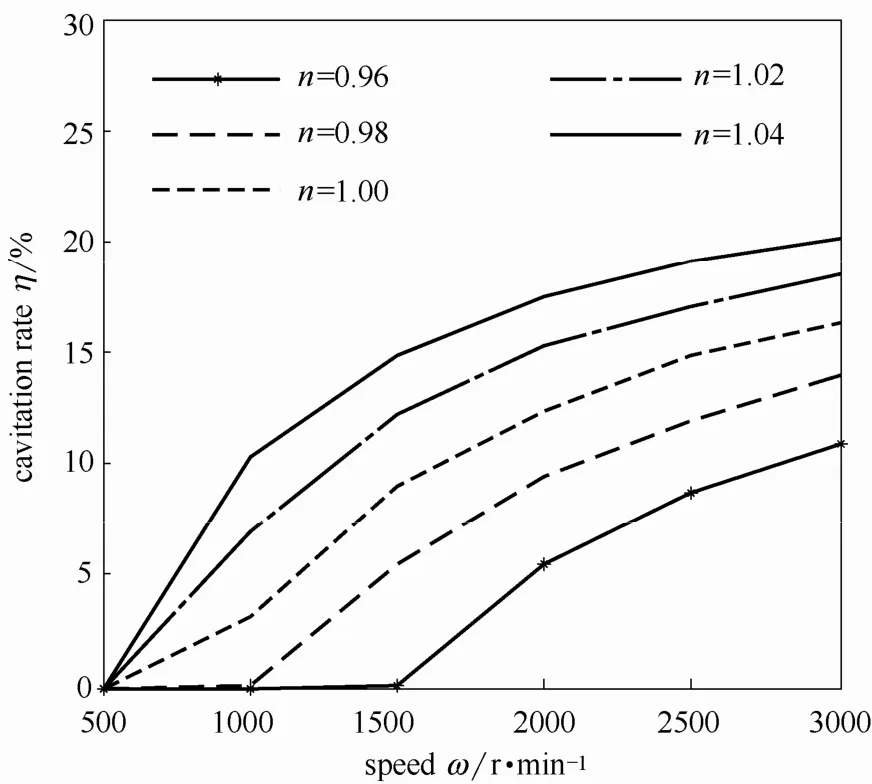
图11 转速对空化率的影响Fig.11 Influence of speed on cavitation rate

结合图10和图11，在较低转速下，空化率较低，转速升高所带来的承载能力提升抵消了空化产生对液膜承载能力的削弱，综合作用结果为液膜承载能力增强；随着转速的进一步增大，空化率增大，空化对液膜承载能力的削弱效果得以体现，抵消了转速升高所带来的承载能力提升，综合作用结果为液膜承载能力逐渐减弱；当转速继续增大时，空化率增大并呈现平稳的趋势，此时液膜承载能力变化也趋于平稳。

综上所述，转速和空化对液膜承载能力的综合作用，出现了图10所示的变化规律。相同转速下，幂律指数对液膜承载能力和空化率的影响在 3.2.1节中作了分析，这里不再赘述。

3.3.2 对摩擦扭矩的影响 图 12所示为密封端面的摩擦扭矩随转速的变化规律。由图可知：转速增大，摩擦扭矩近似线性增加，不同n值下的摩擦扭矩有相同变化规律，整体趋势保持一致。这是由于摩擦扭矩是由旋转方向的黏性剪切力产生的，而黏性剪切力主要受转速影响。图中计算结果表明，在相同转速下，随着n值的增加，摩擦扭矩减小，但其影响较小，其原因已在3.2.2节中进行了分析。

3.3.3 对泄漏量的影响 图 13所示为液膜密封的泄漏量随转速的变化规律。随着转速的增大，泄漏量逐渐增大。不同n值下的泄漏量的变化规律具有相似性。这是由于速度增加，液膜密封的动压效应增强导致泵送量增大，宏观表现为泄漏量增大。图中的计算结果表明，在相同转速下，随着n值的增加泄漏量也随之增大，其原因在3.2.2节中进行了分析。

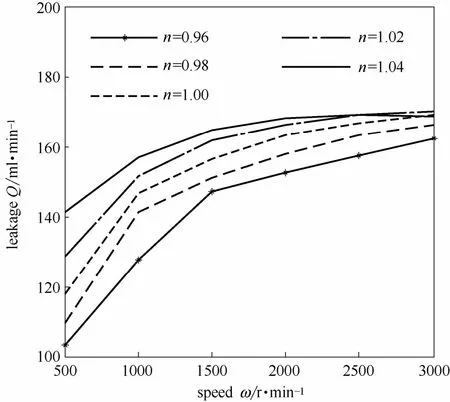
图13 转速对泄漏量的影响Fig.13 Influence of speed on leakage

3.4 压差对性能参数的影响

为探究压差对液膜密封流体动压性能参数的影响，本文计算了不同压差下的性能参数。内径处压力pi的取值范围为 0.2～1.2 MPa，外径处压力po=0.1 MPa，即内外径压差在0.1～1.1 MPa。

3.4.1 对承载能力和空化率的影响 图 14所示为液膜承载能力随压差的变化规律。由图可知，压差越大，液膜承载能力越强，不同n值下的承载能力有相同的变化规律。这是由于压差越大，流体静压提升，密封端面液膜压力整体提高，使液膜承载能力增强。

由图14和图15可知：在0.1 MPa的压差下，随着n值的增大，液膜承载能力减弱，这是由于小压差下端面空化严重，空化对液膜承载能力的影响占主导地位，而幂律指数n的增大使空化增强，在一定程度上使液膜承载能力下降；在1.1 MPa压差下，在膜厚增大的槽区边界处负压也得到一定程度的提高，此处的液膜压力不易达到空化压力，空化率快速下降直至空化不再发生，此时空化对液膜承载能力的影响减弱，随着n值的增大，流体的剪切稀化特性减弱，剪切稠化特性增强，黏度的增大使动压效应增强，液膜承载能力增加。压差在0.1～1.1 MPa时，液膜承载能力受流体非牛顿特性和空化综合作用，性能曲线出现交错。

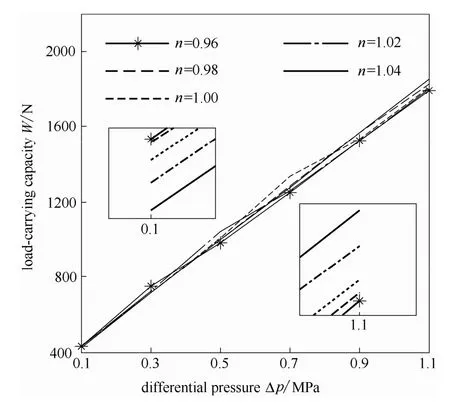
图14 压差对承载能力的影响Fig.14 Influence of differential pressure on load-carrying capacity

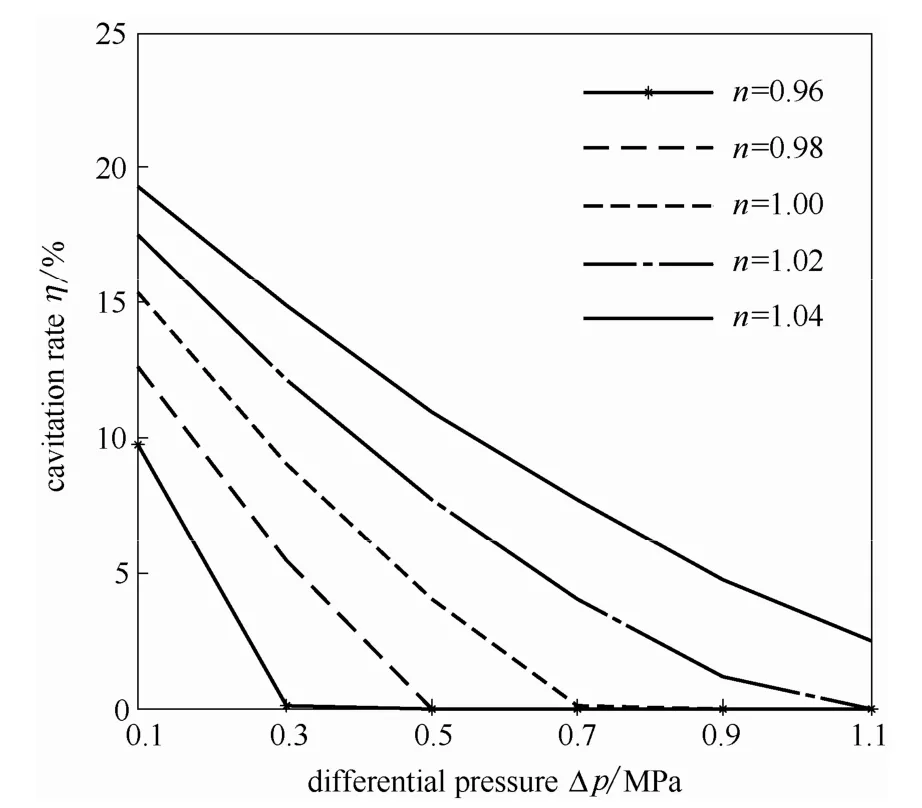
图15 压差对空化率的影响Fig.15 Influence of differential pressure on cavitation rate

3.4.2 对摩擦扭矩的影响 图 16所示为密封端面摩擦扭矩随压差的变化规律。由图可知，摩擦转矩随着压差的增大均呈现先增大后平稳的趋势，不同n值下的摩擦扭矩具有相似的变化规律，其增幅很小。n=1.04时，1.1 MPa压差下的摩擦扭矩相比于0.1 MPa下的摩擦扭矩，增幅约为0.81%。

结合图15和图16，随着压差的增加，密封端面压力整体抬升，空化率逐渐减小直至为零，由于空化区的摩擦扭矩小于全液膜区，空化的减小造成摩擦扭矩在小范围内的增加，当空化消失后，摩擦扭矩不再随压差的改变而改变。由图16可知，相同压差下，随着n值的增大，摩擦扭矩减小，其原因在3.2.2节中进行了分析。

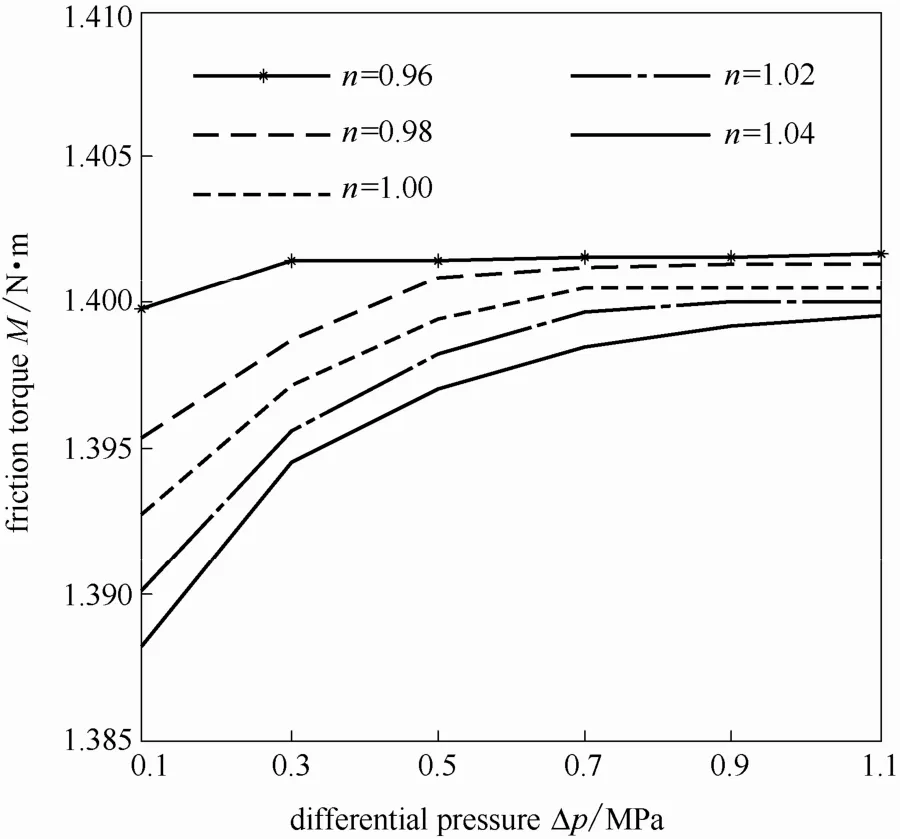
图16 压差对摩擦扭矩的影响Fig.16 Influence of differential pressure on friction torque

3.4.3 对泄漏量的影响 图 17所示为泄漏量随压差的变化规律。由图可知，随着压差的增加，密封端面泄漏量近似线性增大，不同n值下的泄漏量的变化规律具有相似性。这是由于端面泄漏量受径向压力梯度影响，压差增大，造成密封端面径向压力梯度增大，从而使泄漏量增大。

4 结 论

（1）本文考虑润滑流体的非牛顿特性，建立了基于幂律模型的液膜密封分析模型，并对其进行了有限差分离散和数值求解，探究了幂律指数n对螺旋槽液膜密封流体动压性能参数的影响规律，为完善液膜润滑及密封机理提供可靠依据。

（2）较小的幂律指数具有明显的抑制空化作用，使液膜承载能力增强，在一定程度上使摩擦扭矩增加，泄漏量减小；随着操作参数的改变，不同幂律指数下的密封流体动压性能参数变化规律具有相似性。

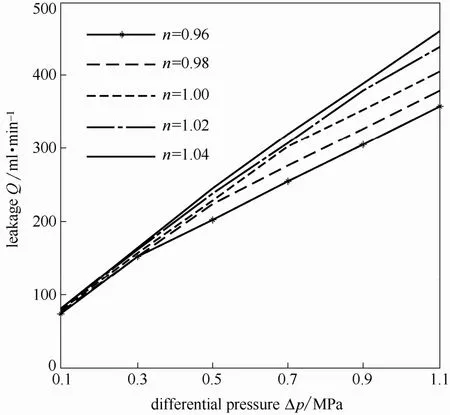
图17 压差对泄漏量的影响Fig.17 Influence of differential pressure on leakage

（3）幂律指数对液膜密封流体动压有较为显著的影响，在实际应用中，应综合考虑幂律指数对各性能的影响，选用合理的润滑流体。

（4）本文主要考虑了流体的非牛顿特性对液膜密封流体动压性能的影响，温度作为一个对流体黏度有重要影响的因素，将在后续工作中进行研究。

符 号 说 明

hg,h0——分别为槽深和非槽区膜厚，μm

g——开关函数

M——摩擦扭矩，N·m

m——稠度指数，Pa·sn

NG——螺旋槽数目

n——幂律指数

p——密封端面膜压，MPa

pc——空化压力，MPa

pi——内径处压力，MPa

po——外径处压力，MPa

Q——体积泄漏量，ml·min-1

rgi,rgo——分别为密封环内、外槽根半径，mm

ri,ro——分别为密封环内、外半径，mm

W——液膜承载能力，N

α——螺旋槽角，(°)

β——流体体积弹性模量，N·m-2

η——空化率，%

θc——单周期计算区域圆周角，rad

θL,θG——分别为单个台区和槽区圆周角，rad

μ——密封面间隙流体动力黏度，Pa·s

ρ,ρc——分别为液膜区密度和空化区密度，kg·m-3

φ——通用变量

ω——密封面旋转速度，r·min-1

下角标

i,j,max——分别为计算域周向、径向网格节点数及最大值

new,old——分别为当前和上一次迭代过程变量值

p——差分中心节点

w,e,n,s——分别为控制体积西、东、北及南侧边界

[1]陈晓嵩.螺旋槽液膜密封在炼油厂富气压缩机上的应用[J].润滑与密封,2002,27(5)：91-94.CHEN X S.Application of spiral groove liquid seal on the rich gas compressor of refinery[J].Lubrication Engineering,2002,27(5)：91-94.

[2]王衍,孙见君,马晨波,等.液膜及气膜非接触式机械密封的对比分析[J].润滑与密封,2013,38(3)：111-116.WANG Y,SUN J J,MA C B,et al.Comparative analysis of non-contact mechanical seals with liquid and gas film[J].Lubrication Engineering,2013,38(3)：111-116.

[3]刘铁汉,蒋利军,游艺,等.丁二烯螺杆压缩机泄漏分析与改造[J].化工机械,2005,32(2)：113-116.LIU T H,JIANG L J,YOU Y,et al.Leakage analysis and modification of butadiene screw compressor[J].Chemical Engineering & Machinery,2005,32(2)：113-116.

[4]QIU Y,KHONSARI M M.On the prediction of cavitation in dimples using a mass-conservative algorithm[J].Journal of Tribology,2009,131(4)：41702-41711.

[5]赵中,彭旭东,盛颂恩,等.多孔扇形分布端面机械密封性能的数值分析[J].化工学报,2009,60(4)：965-971.ZHAO Z,PENG X D,SHENG S E,et al.Numerical analysis of laser textured mechanical seals with a porous sector face[J].CIESC Journal,2009,60(4)：965-971.

[6]李振涛,郝木明,杨文静,等.螺旋槽液膜密封端面空化发生机理[J].化工学报,2016,67(11)：4750-4761.LI Z T,HAO M M,YANG W J,et al.Cavitation mechanism of spiral groove liquid film seals[J].CIESC Journal,2016,67(11)：4750-4761.

[7]裘祖干,陈伯贤.非牛顿流体的非定常雷诺方程在动载径向滑动轴承中的应用[J].内燃机学报,1986,(4)：83-92.QIU Z G,CHEN B X.Application of unsteady Reynolds equation for non-Newtonian fluid in dynamic load journal bearing[J].Transactions of CSICE,1986,(4)：83-92.

[8]沈萌红,周桂如.假塑性流体润滑有限宽向心轴承的热流体动力分析[J].浙江大学学报(工学版),1989,(3)：377-387.SHEN M H,ZHOU G R.Thermal fluid dynamic analysis of a finite width mandrel lubricated by pseudoplastic fluid[J].Journal of Zhejiang University (Engineering Science),1989,(3)：377-387.

[9]EL-SHERBINY M,SALEM F,EL-HEFNAWY N.Optimum design of hydrostatic journal bearings(Ⅲ)：Design procedure[J].J.Eng.Appl.Sci.; (United States),1986,3：1/2.

[10]SINGH C,NAILWAL T S,SINHA P.Elastohydrostatic lubrication of circular plate thrust bearing with power law lubricants[J].Journal of Tribology,1982,104(2)：243-247.

[11]CHIPPA S P,SARANGI M.Elastohydrodynamically lubricated finite line contact with couple stress fluids[J].Tribology International,2013,67(4)：11-20.

[12]SHARMA S C,RAJPUT A K.Effect of geometric imperfections of journal on the performance of micropolar lubricated 4-pocket hybrid journal bearing[J].Tribology International,2013,60(7)：156-168.

[13]BOUYAHIA F,HAJJAM M,KHLIFI M E,et al.Three-dimensional non-Newtonian lubricants flows in sector-shaped,tilting-pads thrust bearings[J].ARCHIVE Proceedings of the Institution of Mechanical Engineers Part J.Journal of Engineering Tribology 1994—1996 (vols 208—210),2006,220(4)：375-384.

[14]SHARMA S C,YADAV S K.Performance analysis of a fully textured hybrid circular thrust pad bearing system operating with non-Newtonian lubricant[J].Tribology International,2014,77：50-64.

[15]王涛,黄伟峰,王玉明.机械密封液膜汽化问题研究现状与进展[J].化工学报,2012,63(11)：3375-3382.WANG T,HUANG W F,WANG Y M.Research and progress of mechanical seals operating with vaporization transition[J].CIESC Journal,2012,63(11)：3375-3382.

[16]唐飞翔,孟祥铠,李纪云,等.基于质量守恒的 LaserFace液体润滑机械密封数值分析[J].化工学报,2013,64(10)：3694-3700.TANG F X,MENG X K,LI J Y,et al.Numerical analysis of LaserFace liquid lubricated mechanical seal based on mass conservation[J].CIESC Journal,2013,64(10)：3694-3700.

[17]陈汇龙,吴强波,左木子,等.机械密封端面液膜空化的研究进展[J].排灌机械工程学报,2015,33(2)：138-144.CHEN H L,WU Q B,ZUO M Z,et al.Overview on liquid film cavitation in mechanical seal faces[J].Journal of Drainage and Irrigation Machinery,2015,33(2)：138-144.

[18]JAKOBSSON B,FLOBERG L.The finite journal bearing considering vaporization[J].Wear,1958,2(2)：85-88.

[19]OLSSON K O.Cavitation in dynamically loaded bearing[J].Wear,1967,55(2)：1-60.

[20]QIU Y,KHONSARI M M.Performance analysis of full-film textured surfaces with consideration of roughness effects[J].Journal of Tribology,2011,133(2)：021704(1-10).

[21]赵一民,魏超,苑士华.两种空化边界条件下的旋转密封润滑状态分析与试验[J].兵工学报,2014,35(12)：1937-1943.ZHAO Y M,WEI C,YUAN S H.Analysis and experiment of lubrication condition of rotary seal based on two cavitation boundary conditions[J].Acta Armamentarii,2014,35(12)：1937-1943.

[22]彭旭东,佘宝瑛,孟祥铠,等.不同排布方向性椭圆孔液体润滑机械密封性能的研究[J].摩擦学学报,2013,33(5)：481-487.PENG X D,SHE B Y,MENG X K,et al.Sealing performance of liquid-lubricated mechanical seals with different arrangements inclined elliptical dimples[J].Tribology,2013,33(5)：481-487.

[23]ELROD H G.A cavitation algorithm[J].Journal of Tribology,1981,103(3)：350-354.

[24]BREWE D E.Theoretical modeling of the vapor cavitation in dynamically loaded journal bearings[J].Journal of Tribology,1986,108(4)：628-638.

[25]VIJAYARAGHAVAN D,JR KEITH T G.Development and evaluation of a cavitation algorithm[J].Tribology Transactions,1989,32(2)：225-233.

[26]FESANGHARY M,KHONSARI M M.A modification of the switch function in the elrod cavitation algorithm[J].J.Chem.Soc.,2011,32(6)：5247-5251.

[27]胡纪滨,刘丁华,魏超.径向直线槽端面密封空化特性数值模拟[J].摩擦学学报,2011,31(6)：551-556.HU J B,LIU D H,WEI C.Numerical simulation for cavitation of radial grooved face seals[J].Tribology,2011,31(6)：551-556.

[28]赵一民,苑士华,胡纪滨,等.基于质量守恒边界条件的螺旋槽旋转密封性能分析[J].机械工程学报,2014,50(22)：142-149.ZHAO Y M,YUAN S H,HU J B,et al.Performance analysis of spiral-groove rotary seals considering mass conserving boundary condition[J].Journal of Mechanical Engineering,2014,50(22)：142-149.

[29]郝木明,庄媛,章大海,等.考虑空化效应的螺旋槽液膜密封特性数值研究[J].中国石油大学学报(自然科学版),2015,39(3)：132-137.HAO M M,ZHUANG Y,ZHANG D H,et al.Numerical study on sealing performance of spiral groove liquid film seal considering effects of cavitation[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(3)：132-137.

[30]DOWSON D.A generalized Reynolds equation for fluid-film lubrication[J].International Journal of Mechanical Sciences,1962,4(2)：159-170.

[31]LEBECK A O.Principles and Design of Mechanical Face Seals[M].John Wiley & Sons,1991：109-249.

[32]DIEN I K,ELROD H G.A generalized steady-state Reynolds equation for non-Newtonian fluids,with application to journal bearings[J].Journal of Tribology,1983,105(3)：385-390.

date：2017-05-22.

Prof.HAO Muming,haomm@upc.edu.cn

supported by the National Natural Science Foundation of China (51375497) and the Key Research Program of Dongying(2016YF01).

Hydrodynamic performance of spiral groove liquid film seals based on JFO boundary condition and power law model

WANG Yunlei,HAO Muming,LI Zhentao,LI Yongfan,SUN Xinhui,XU Lushuai
(Institute of Sealing Technology,China University of Petroleum,Qingdao266580,Shandong,China)

The performance of liquid film seals is significantly affected by non-Newtonian behavior of lubricating fluids at seal interface.A mathematical model of spiral groove non-Newtonian liquid film seal was established by combination of mass conservation at JFO cavitation boundary condition and power law model of non-Newtonian fluids.The governing equation was discretized by finite difference method and solved by SOR iterative algorithm to obtain liquid film pressure distribution.The effects of non-Newtonian fluids on sealing performance were analyzed,including load-carrying capacity,leakage,friction torque,and cavitation occurrence in liquid film.The results indicate that with the increase of power law index,the load-carrying capacity first increases then decreases but the leakage and cavitation rate always increase and the friction torque consistently decreases.At power law indexn=0.96,non-Newtonian fluids had increase by 4.6% in the load-carrying capacity and 0.3% in the friction torque but decrease by 98.6% in the cavitation rate of sealing face and 5.8% in leakage than Newtonian fluids.When operating parameters were changed,non-Newtonian fluids with various power law indices showed similar trending behavior of liquid film hydrodynamic performance.Suitable lubricant selection is important to improve sealing performance of liquid films.

spiral groove liquid film seals; power law model; non-Newtonian fluids; JFO boundary condition;hydrodynamic performance

TH 117.2

A

0438—1157（2017）12—4665—10

10.11949/j.issn.0438-1157.20170660

2017-05-22收到初稿，2017-06-25收到修改稿。

联系人：郝木明。

王赟磊（1993—），男，硕士研究生。

国家自然科学基金项目（51375497）；东营市重点研发项目（2016YF01）。