思维导图在解析几何解题中的应用

江苏省苏州市吴中区甪直高级中学 姜爱美 冯中芹

思维导图在解析几何解题中的应用

江苏省苏州市吴中区甪直高级中学 姜爱美 冯中芹

高中数学新课程标准的课程基本理念是倡导学生自主探索、动手实践、合作交流、阅读自学等学习数学的方式，发挥学生学习的主动性，使学生的学习过程成为“再创造”的过程。同时，新课程标准设立了许多学习活动，为学生形成多样性的学习方式创造了有利的条件，以激发学生的数学学习兴趣，通过自学学习过程，使学生养成独立思考、积极探索的习惯，让学生体验数学发现和创造的历程，发展他们的创新意识。

解析几何是近几年高考的重点，但解析几何的概念和解题方法理解起来比较困难，学生对解析几何的认识不深入，对解析几何的应用掌握不理想，使得学生对解析几何的解答产生了畏惧心理，怕下笔，很难得到分。利用思维导图学习既有利于学生理清知识层次,也能显示出解题的思维过程。思维导图是一种简单有效的用图形来表达思维、知识的表征工具, 它最大的优点是采用结构化的放射性思考模式，充分发挥左右脑的天赋，符合大脑的运作方式。因此，思维导图被誉为强力学习、记忆和思维训练的方法，能大幅提升学生的学习效率以及掌握新知识的能力。

一、思维导图在解析几何解题反思中的应用

解题反思是解析几何中一个必不可少的环节。根据思维导图的发散性特点，我们可以探索解题思路和进行解题后的反思。通过思维导图，能使学生的知识应用更熟练、更深刻，并学会一些解决问题的方法和技巧，积累一些解题经验。

在做题后，指导学生反思题中所涉及的知识，包括概念、公式、定理。这样做既可以让学生复习到一些基本概念，并且能让学生找出没有掌握的概念，达到进一步学习薄弱知识的目的。反思解题思想，用思维导图画出来，可以使抽象的思维直观化。反思题目应当注意的地方，让学生再遇到此类题目时不犯相同的错误。

例1 已知曲线C：y2=4x，过点P(0,2)的直线l与曲线C交于A，B 两点，且直线l与x轴交于点E 。试问否为定值？若是，求出此定值；若不是，请说明理由。

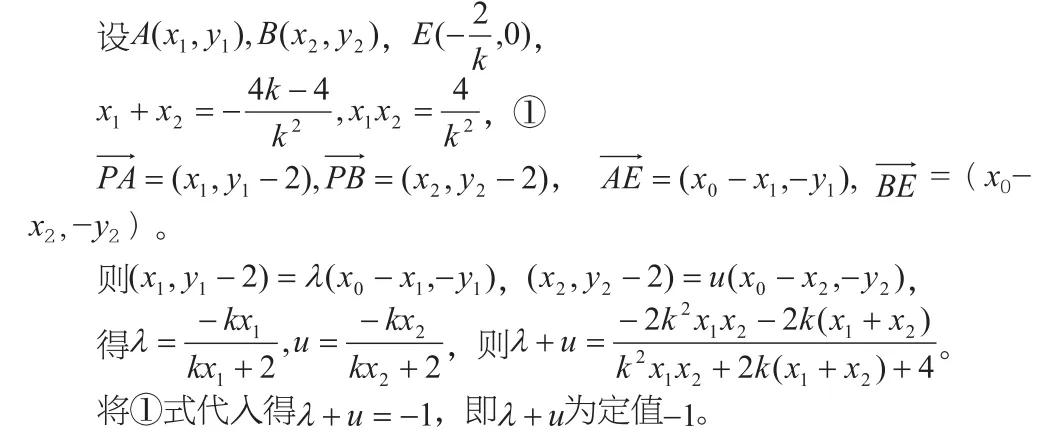
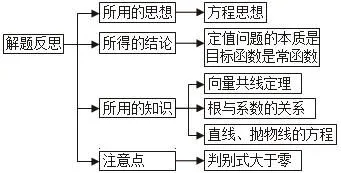
在解题后，通过思维导图进行解题反思，反思自己的解题思路，总结解题规律，并发现自己在解题中显露出的知识能力的缺陷，同时培养学生的归纳、整理、应用知识的能力。反思问题涉及了哪些数学思想方法，这些思想方法是如何运用的，运用的过程中有什么特点，是否在其他情况下运用过，运用时有什么区别、联系，总结出规律，归纳出解决问题的一般方法来。

二、思维导图在解析几何解题变式中的应用

所谓“变式”，就是指教师有目的、有计划地对命题进行合理的转化，即教师可不断更换命题中的非本质特征；变换问题中的条件或结论；转换问题的内容和形式；配置实际应用的各种环境，但应保留好对象中的本质因素，从而使学生掌握数学对象的本质属性。利用思维导图指导学生对题目变式进行整理，一题多变。改变条件或结论，看问题有什么变化，解决问题的方法有什么改变，也可以将当前的命题推广到一般情况，进行发散思维，当然，不是每一个题目都有变式。另外，利用思维导图鼓励学生多思考，激发其创造性。对于分支变式，可以另画导图加以发散，这样就既在整体上有了把握，也在解题思想上有了认识。

通过思维导图总结弦中点以及求直线与圆锥曲线相交弦的中点问题的常用方法，使得学生对所学知识有系统的认识。同时，思维导图能够很好地体现变式与例题，变式与变式之间的内在联系，引导学生对解题思路和方法进行总结和反思，以提高分析问题、解决问题的能力，养成良好的数学学习习惯。

三、思维导图在解析几何解题方法选择中的应用

圆锥曲线是解析几何的重要内容之一，也是近几年高考命题的热点和重点，主要考查的内容是圆锥曲线的概念和性质、直线和圆锥曲线的位置关系等。关于圆锥曲线问题解决的基本方法是点参法、斜参法，而方法（点参、斜参）的选择是学生解决圆锥曲线问题的一个难点，学生在解决这类问题时，往往因为方法的选择而导致计算上的困难，最后时间过去了，题目还是没有做出来。因此，在解题方法选择前，如果先画出各个方法的思维导图，然后进行比较，看解题方法在简易、严谨等方面有什么不同，比较各种方法的优劣，并确定最好的解题办法，这样就能为学生在高考中节省时间。

（1）求直线AB的方程；

（2）若点P为椭圆c上异于A、B的动点，且直线AP,BP)分别交直线y=x于点M、N，证明：OM.ON为定值。

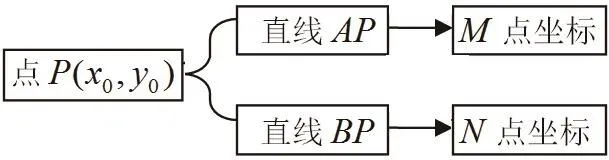
点参法的思维导图

方法二（斜参法），设直线BP的斜率为k。

斜参法的思维导图

从这两个思维导图上看，斜参法的思维导图比点参法的思维导图要复杂得多，那么计算过程就复杂。另外，点参法的思维导图具有对称性，即求M点坐标与求N点坐标的过程是一样的，这样给计算带来了很大的方便。所以，通过思维导图的对比，学生很容易发现点参法比较简单，使学生节省了时间。

通过上述思维导图，要求每位同学能够形成知识网络，总结主要数学思想和数学方法。在实际教学中，需要学生协同合作，每人负责落实某一块的思维导图，完成后再组合成新的思维导图。这样的操作加强了同学们之间的合作交流，同时也培育了他们的整体思维能力。利用思维导图让学生学会整理解析几何的知识、题型和方法，更积极地参与到教学中来，提高学习效率。利用思维导图指导高中生学习解析几何能够提高学习的针对性，让学生知道解析几何知识的来龙去脉，在他们的头脑中形成清晰明了的知识网络，利用思维导图让学生进行解题后的反思，促进知识的深入理解，最终提高学生解决问题的能力。