驶入角对跑偏测量值的贡献量分析

王海星，欧先锋，涂 兵

(湖南理工学院 a.机械工程学院；b.信息与通信工程学院；c.复杂系统优化与控制 湖南省普通高等学校重点实验室,湖南 岳阳 414006)

驶入角对跑偏测量值的贡献量分析

王海星a，欧先锋b，c，涂 兵b，c

(湖南理工学院 a.机械工程学院；b.信息与通信工程学院；c.复杂系统优化与控制 湖南省普通高等学校重点实验室,湖南 岳阳 414006)

在汽车行驶跑偏下线检测环节中常常利用比例换算、代数加减的方法获得测试车辆的跑偏值。尽管测试车辆驶入角只是跑偏测试结果的一个控制变量，影响测试系统跑偏量输出值的因素众多。通过分析驶入角对跑偏测量值的贡献量，同时对残差进行分析论证，严格遵循统计学和概率论的思维针对具体情形细致分析了驶入角对跑偏测试结果的影响规律。如何检验多维正态分布是工程应用中的棘手问题，本文从变量背后的实际意义出发，创造性地通过计算变量之间的任意线性组合，转化为运用正态概率纸检验一维正态性问题，分析所得结果均符合理论和实际情况。实际应用中，如何透视出大量数据背后的内在规律，本文相关处理思路与方法富有借鉴意义。

行驶跑偏；残差分析；正态性检验

目前，基于机器视觉和图像处理的汽车行驶跑偏自动检测系统[1]通过安装在龙门架上的工业相机采集车辆在测试点处的高分辨率图像，通过主机对图像的识别和处理，计算出车辆在测试路段上的跑偏量、跑偏方向及行驶速度，同时计算车辆的驶入角[2]。检测系统要求试车员必须在测试准备区调整汽车行驶方向与道路中心基准线对齐，并且达到直线行驶的稳定状态后，才能进行检测。事实上，测试车辆的驶入角误差必定存在。尽管汽车出现行驶跑偏的故障跟驶入角之间并非因果关系，但在进行跑偏测试的实际操作过程中，由于试车员操作上的疏忽，容易导致由检测系统所计算出的实际汽车行驶测量值因为车辆驶入角度值的微小变化而包含巨大的误差[3]，甚至引起检测系统对测试车辆本身是否存在行驶跑偏故障的误判。因此，本文通过分析驶入角对跑偏测量值的贡献，揭示驶入角对跑偏测试结果的影响规律，为后续优化跑偏量的计算方法[4]、提高系统测试精度提供理论依据。

1 随机变量之间的独立性检验

在应用统计学中，常常需要根据实际观测结果来检验随机变量之间的独立性。一般而言，若总体中的个体能够根据不同的属性A与B进行分类，根据属性A的所有可能取值不同分成r个不同组A1，A2，...，Ar；根据属性B的所有可能取值不同又分成s个不同组B1，B2，...，Bs；对(X，Y)进行n次独立观测分别记录事件(X∈Ai，Y∈Bj)出现的频数mij(i=1，2，...，r;j=1，2，...，s)，将所得结果列成r×s格列联表。

列联表从应用统计学的角度证明各个属性彼此有无关联，也就是表明各个属性独不独立[5]。在本文中，要分析驶入角X对跑偏测量值Y的贡献量，首先要证明X与Y是否有关？

取统计量

(1)

当原假设H0成立时，且n很大时，由拟合优度检验可知

χ2～χ2(υ)，υ=(r-1)(s-1)

(2)

即上述统计量近似服从χ2分布[6]，统计量对应的自由度为(r-1)(s-1)。

并且可得H0的拒绝域为

(3)

1.1 驶入角测量值和跑偏测量值的列联表

记测试车辆驶入角测量值为随机变量X，车辆行驶跑偏测量值为随机变量Y。作出它们的交叉列联表，进行变量之间独立性关系的检验[7]。

将从检测线反馈的X和Y值，按照驶入角大小和跑偏测量值的合格标准分类记录到表1中。

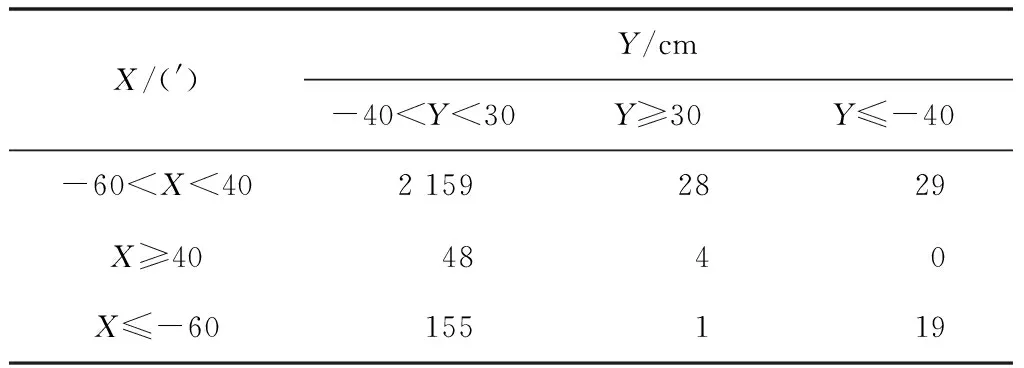
表1 (X，Y)数据点交叉列联表

1.2 卡方统计检验

卡方统计检验用于检验交叉列联表中变量之间的相互独立性问题，相应的假设检验原理为：

给定原假设H0：列变量与行变量二者相互独立。

如果原假设成立，则期望频数为：

(4)

其中：ri为第i行所有频数之和；cj为第j列所有频数之和；n是样本容量。

经计算，X和Y期望频数分布如表2所示。

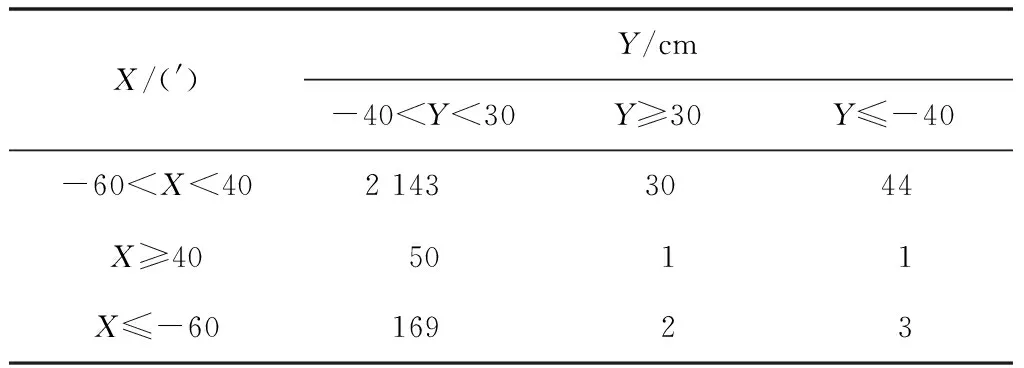
表2 (X，Y)数据点期望频数

构造χ2统计量

(5)

其中：fij，eij分别是第i行j列所表示类别的实际频数、期望频数。列表计算如表3所示。

χ2统计量计算结果为：

(6)

1.3 统计决策

由于，当H0成立时，且n很大时，可以得到如下关系：

χ2～χ2(υ)，υ=(r-1)(s-1)

(7)

并且可得H0的拒绝域为

(8)

根据χ2统计量表，查得拒绝域临界取值为：

(9)

因为

(10)

故拒绝H0：列变量Y与行变量X之间相互独立。

一般而言，χ2值越小，表明两变量间的关系越弱；χ2值越大，表明两个变量间的关系越强[8]。

由显著性水平α=0.005可知，有99.995%的把握认为测试车辆驶入角X与车辆行驶跑偏量Y之间不独立，存在关联。

接下来分情况讨论X与Y之间的关系。

2 Y较合理而X偏大的情形

Y的观测值落在合理的取值区间范围内，即Y的取值区间为[-40，30]，而X的取值>40′。这种情形所对应的实际情况是：进行车辆行驶跑偏检测时，驾驶员没有严格遵从操作规程，在驾驶汽车通过试验准备区的过程中，没有利用试验道路地面中心基准线很好地引导调整汽车车身纵轴线与基准对齐，而是车辆驶入角向右偏大。且由行驶跑偏自动检测系统计算所得的Y落在合格范围[-40，30]内，说明测试车辆本身并没有严重的行驶跑偏现象(或故障)。该情形下样本数据取值分布状况如表4所示。

表4 样本数据取值分布状况

2.1 简谐函数和的形式初步拟合

首先尝试采用简谐函数和的形式进行初步拟合，其表达式形式为：

(11)

经计算各项系数取值如表5所示。

2.1.1 相关指数R2评价

实际应用中常常通过相关指数R2来评价回归拟合的实际效果。

(12)

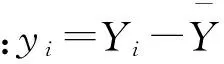
表5 各项系数取值

2.2 跑偏量与驶入角变量线性回归模型

上述采用简谐函数和的形式进行初步拟合分析计算说明，X与Y数据点的分布具有很大的波动性。

测试车辆行驶跑偏量除了受车辆驶入角的影响外，还受很多其他因素的影响，例如装配过程、车辆质心位置、轮胎锥形侧向力、轮胎气压、阻滞力、车轮定位参数等等。事实上，我们无法知道X和Y之间的确切关系是什么，这种情况下，由于Y在合格区间[-40，30]内，表明单从车辆行驶跑偏检测的指标来说，汽车没有行驶跑偏的故障(或问题)。而经由行驶跑偏自动检测系统测量得的Y并不为0，Y介于向左跑偏25 cm到向右跑偏19.7 cm之间，与之相对应的X超过40′，属于X偏大的情形。为此，可以推断Y与X较大之间存在着密切关联。

另外，根据对样本数据的观测，Y与X之间有线性回归的趋势。因此，可以尝试用样本建立变量之间的线性回归模型。线性回归模型的整体表达式可采用如下形式：

(14)

b和a是模型的未知参数，ε是y与Ey=bx+a之间的随机误差。一般而言，ε的均值E(ε)=μ(一般接近于0)，方差D(ε)=σ2>0。

这里只是利用线性回归方程来近似这种关系。产生随机误差ε受上面所有提及的影响因素以及近似关系的制约，还有斜率与截距的估算误差等等。

根据问题需选取X为自变量x，Y为因变量y，经计算

可知回归方程为：

y=-2.372 8+0.019 7x

(15)

2.2.1 检验模型-残差作分析

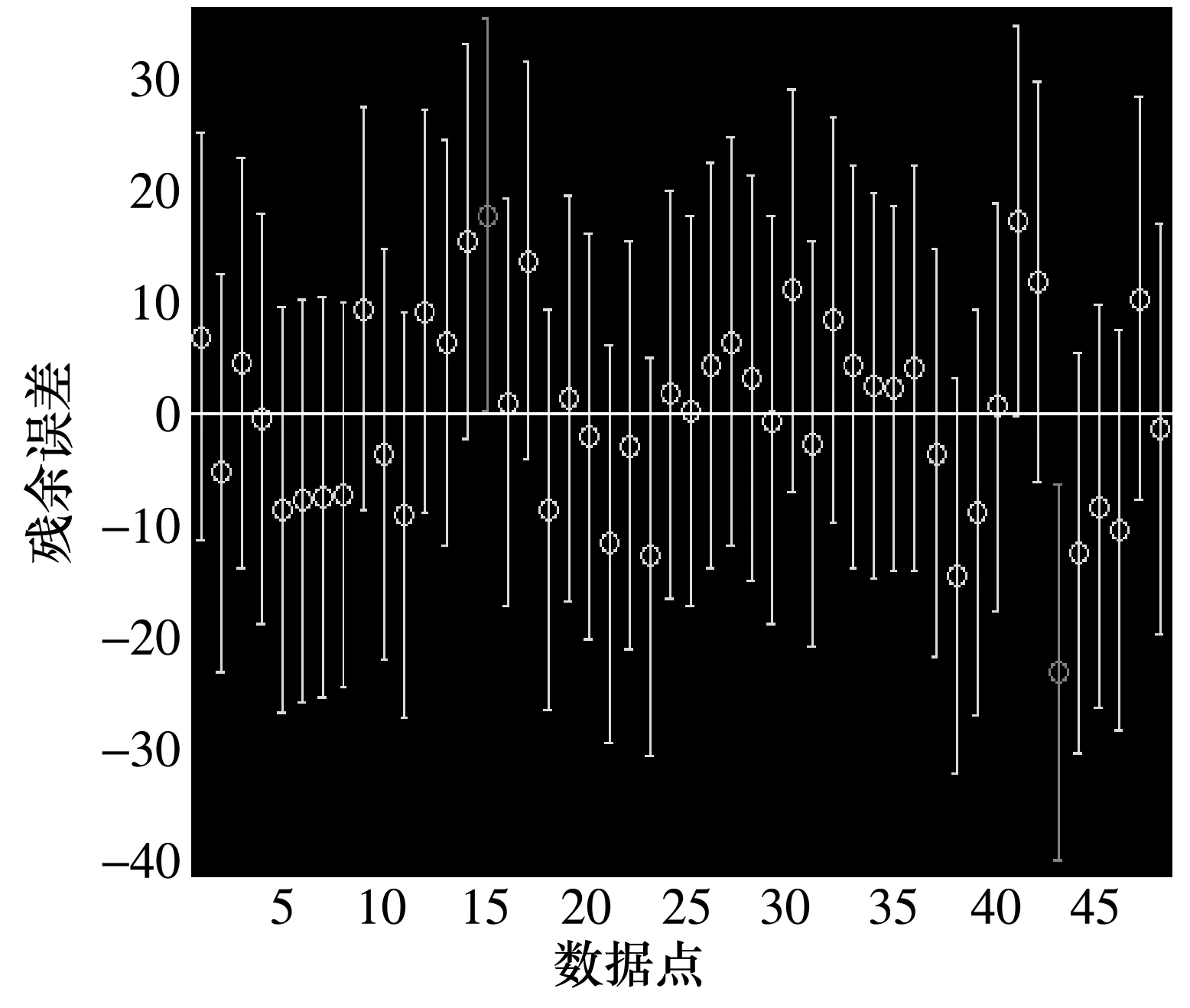
图1 回归分析所得残差

从图1能够看出，除第15、44个数据外，样本数据中其他残差分布都聚集在零点附近，同时零点都包括在残差所对应的置信水平的区间以内，上述观察表明原始样本数据同所选的回归模型y=-2.372 8+0.019 7x符合程度很高。而第15、44个数据点则属于原始样本中的异常点。

另外，对残差作分析，检验看它是否服从正态分布，是否与前文中所提出的假设相一致。

1)作残差概率的具体分布图如图2所示。

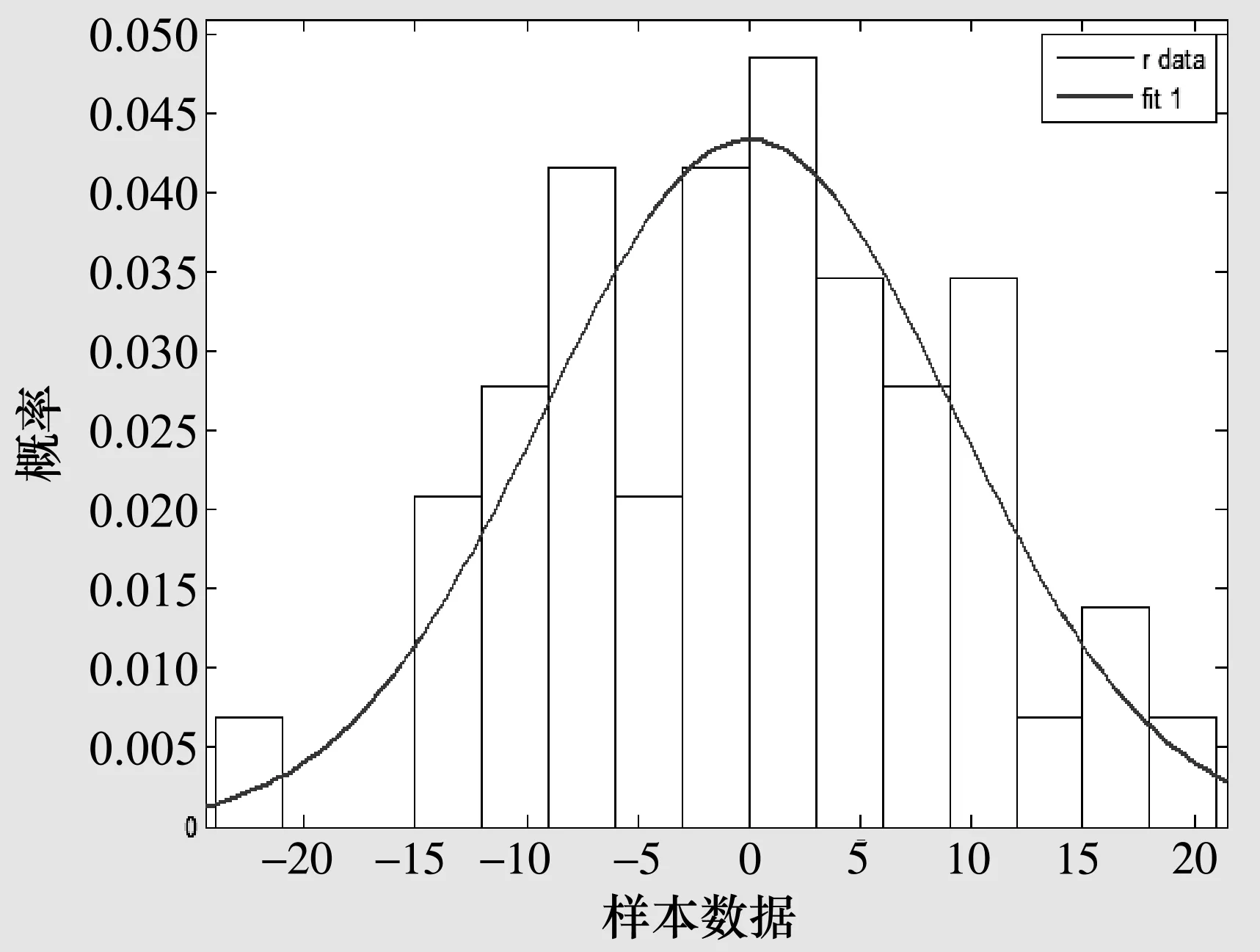
图2 残差概率的具体分布

由图2可知，残差可能服从正态分布，因此，为了确认残差分布情况有必要对残差作正态性检验。

2)经由残差分布的正态性检验可知，残差数据分布在某一条直线的附近。

3)参数估计。估计出该残差的均值为2.035 4e-016，非常接近零。方差为9.192 82，均值的0.95置信区间是[-2.669 3，2.669 3]，方差0.95的置信区间是[7.652 7，11.514 7]。

4)假设检验：已知回归分析的残差服从正态分布，在正态分布的方差不已知的情形下，检验它的期望均值与0是否相等。检验结果：h=0， sig=1，ci=[-2.669 3， 2.669 3]。

检验结果分析：布尔变量h=0表示不可以拒绝原假设，说明第4)步所提出的假设——回归分析所得的残差其均值等于零是合理的；95%的置信区间是[-2.669 3， 2.669 3]，它完全包括0，且精度很高； sig=1，比0.5大很多，没有理由去拒绝原假设。

上述对回归模型所得的残差分析表明，驶入角与跑偏量之间有很强的线性关系，从而也表明所建立的回归模型是有意义的。

2.3 小结

3 X与Y都在较合理范围的情形

X与Y的观测值都落在合理的取值区间范围内，即X在[-60，40]，Y在[-40，30]。这种情形所对应的实际情况是，进行车辆行驶跑偏的检测时，驾驶员较为严格遵从操作规程，在驾驶员驾驶汽车通过试验准备区的过程中，利用试验道路地面中心基准线引导较好地调整了汽车车身纵轴线与基准对齐。而且由行驶跑偏自动检测系统计算所得的Y值落在合格范围[-40，30]内，说明测试车辆不存在严重的行驶跑偏现象(或故障)。

3.1 相关性检验

采用相关系数法来检验X与Y之间是否存在着线性关系。相关系数的计算表达式为

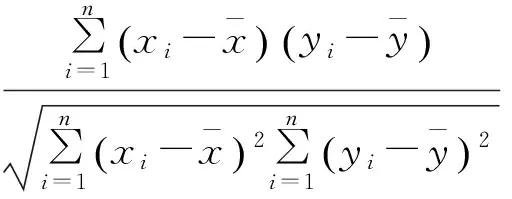
(16)

通常当|ρXY|<0.3时，表示二者之间微相关；当0.3≤|ρXY|≤0.5时，表示二者之间实相关；当0.5<|ρXY|≤0.8时，表示二者之间显著相关；当0.8<|ρXY|≤1时，表示二者之间高度相关[9]。

上述情况中，代入数据后可以计算出X与X的相关系数ρXY=0.17，表明X和Y之间的线性相关性很微弱。

3.2 (X，Y)二维联合分布的未知检验

接下来检验X与Y之间是否存在其他的可能关系。由X与Y构成的点(X，Y)在平面XOY内散点图与二维分布直方图如图3所示。

已知X与Y都服从正态分布，且有，

X～N(-25.41，162)

Y～N(-2.56，10.82)

现在，记X与Y的任意线性组合为随机变量Z，即Z=aX+bY。其中a，b为任意实数。绘制Z的经验分布函数[10]如图4所示。

从图4可以看出，对于任意给定的一组实数a，b，Z的经验分布函数曲线迅速上升，斜率越来越大，图像曲线呈S型，超过曲线轨点后，经验分布函数斜率逐渐减小，曲线平缓上升，经验分布函数图像的上述曲线特征揭示X与Y任意线性组合后的Z很可能服从正态分布。

从随机变量概率纸检验结果可知，任意给定的一组实数，随机变量数据样本集中分布在对应的参考直线附近；少数情形下，随机变量数据样本分布有些偏离对应的参考直线，原因可能在于所讨论的数据范围内，两随机变量与取值区间的长度不完全一致，X取值范围更大一些。因此，排除两随机变量取值区间上的差异，任意给定的一组实数a，b，随机变量Z服从正态分布。因此，任意线性组合Z=aX+bY服从一维正态分布，由随机变量X与Y构成的二维随机变量(X，Y)服从二维正态分布。

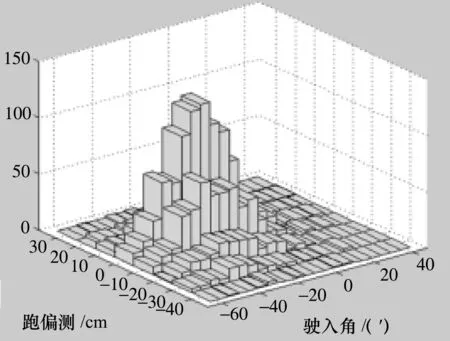
图3 随机点(X，Y)的分布

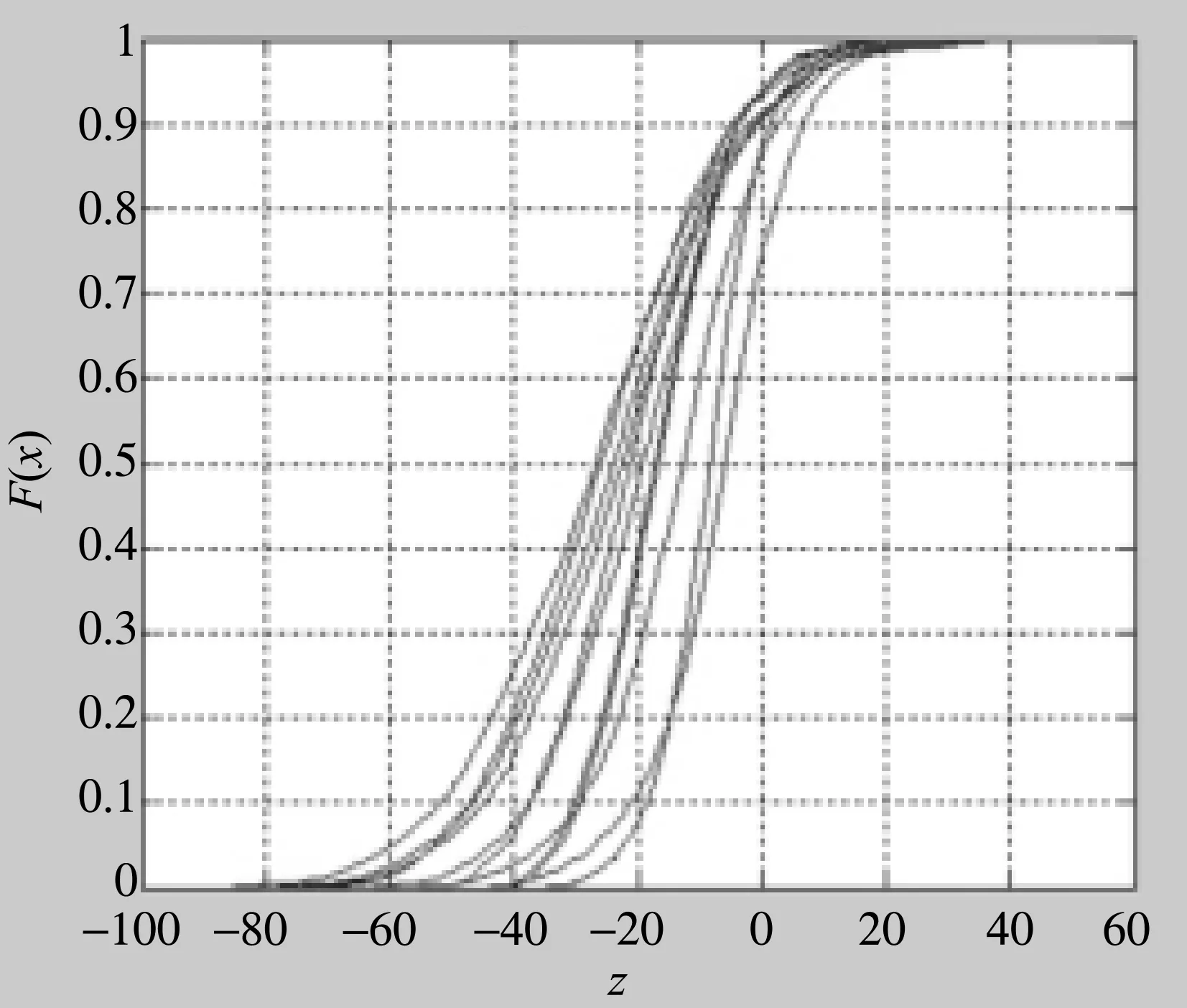
图4 X与Y任意线性组合的经验分布

3.3 X与Y局部独立性

尽管X与Y独立包含了X，Y不相关，但反过来，X，Y不相关，X与Y可以不独立。也就是说，“独立”这个概念要比“不相关”这个概念强。然而，如果由X和Y构成的二维随机变量(X，Y)在服从二维正态分布的情形下，X和Y二者不相关跟X和Y二者相互独立是完全等价互推的概念。

1) 在上述情形下，计算出相关系数ρ=0.17。可以看出相关系数ρXY的值很小。

2) 下面将X的数据研究区域定位到更小的范围，如X的2σ区间为[-40，26]。处于该区域内的样本数据如表6所示

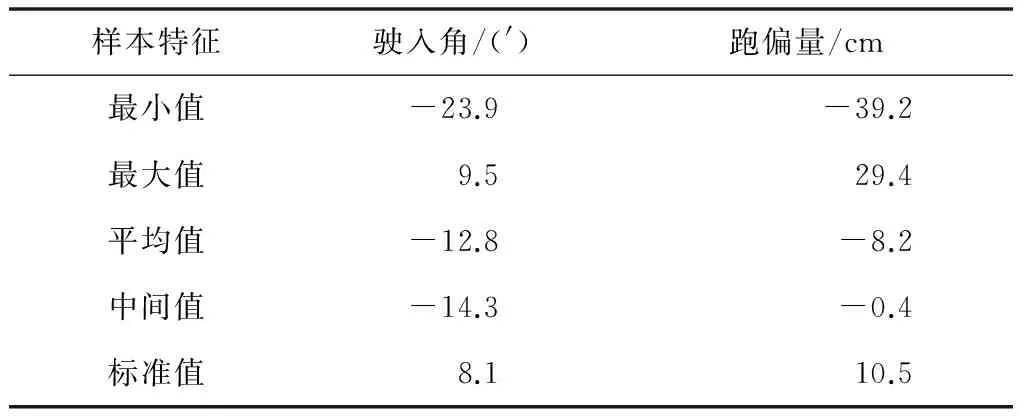
表6 X的1σ区间样本数据取值分布状况

经计算X的1σ区间内的样本数据之间的相关系数ρXY=0.06。

3) 继续将X的数据研究区域定位到[-24，10]。处于该区域内的样本数据如表7所示

表7 X的2σ区间样本数据取值分布状况

经计算，X的2σ区间内的样本数据之间的相关系数X。

上述计算说明，随着X范围的缩小，X与X之间的相关系数X越来越小，同时，(X，Y)服从二维正态分布，因此，随着X范围的缩小，X与Y之间的独立性越来越强，特别是在X的1σ取值区间[-24，10]内，它们二者的相关系数ρXY=0.06，非常接近于0，可以认为X与Y之间是独立的，因此X对Y的贡献量可以忽略不计。

4 结论

由测试系统输出的跑偏量由三部分构成：驶入角对跑偏测量值的贡献量；不受驶入角影响的跑偏量固定值部分(样本回归方程的截距)；其他未知因素产生的随机部分(残差ε)。

尽管在整个区间范围内，X与Y之间不独立，但在较小的X取值范围内，可以认为X与Y是相互独立的，X对Y的贡献量很小，可以忽略不记。这是因为车辆行驶跑偏是由很多随机因素共同决定的一个随机事件，只有当X很大时，它对Y的贡献量才很大，才会对测试系统中Y的输出值产生较大的影响。因此，在跑偏测试过程中测试车辆驶入角是跑偏结果的一个不可或缺的控制因素。同时，对于没有行驶跑偏故障的测试车辆，即Y∈[-40，30]，只要X调整在合理的取值范围内，则对Y的影响可以忽略不计。

[1]杨灿.基于LabVIEW的汽车行驶跑偏测试系统研究开发[D].武汉：武汉理工大学，2010.

[2]崔淑娟.车辆跑偏在线自动检测系统的图像处理技术研究[D].武汉：武汉理工大学，2010.

[3]廖聪.基于汽车跑偏检测系统对车辆行驶跑偏的原因和解决对策的研究[D].武汉：武汉理工大学，2012.

[4]鲁力.汽车行驶跑偏测试系统的设计改进与软件优化[D].武汉：武汉理工大学，2012.

[5]佟毅.关于随机变量独立性的研究[J].石油化工高等学校学报，1994(3)：71-74.

[6]应坚刚，何萍.概率论[M].上海：复旦大学出版社，2006.

[7]张宏礼，王苫社，周晓晶，等.随机变量独立性的一个注记[J].高等数学研究，2010,13(1):114-115.

[8]何书元.概率论[M].北京：北京大学出版社，2006.

[9]贺昌政，梁元第，王桵.数学建模导论[M].成都：成都科技大学出版社，1997.

[10]张德丰.Matlab概率与数理统计分析[M].北京：机械工业出版社，2010.

ContributionAnalysisofEnteringAngletoWanderringTestValues

WANGHaixinga，OUXianfengb，c，TUBingb，c

(a.School of Mechanical Engineering；b.College of Information & Communication Engineering; c. Key Laboratory of Optimization & Control for Complex Systems， Hunan Institute of Science and Technology， Yueyang 414006， China)

Wandering test value is usually obtained through algebraic add and scaling conversion in the wandering test session. The output result of test system is influenced by plenty of factors， and the entering angle is just one of control variable. In this paper， the relationship between entering angle and wandering test value was elaborated according to the statistics thinking mode strictly. Meanwhile， in terms of different cases， the contribution of entering angle to wandering test values was analyzed with residual analysis as well. It is a hot potato as to the verification for the multidimensional normal distribution in engineering application. Based on the actual meaning of the variables， the verification for the multidimensional normal distribution was creatively converted to one-dimensional normality test via normal probability coordinate paper through calculating random linear combination between variables. And the obtained results are in line with the actual situation. The relevant solutions making for discovering the inherent relationship beneath mass data in this paper has a certain reference value.

driving wandering; residual analysis; normal distribution test

10.13542/j.cnki.51-1747/tn.2017.04.006

2017-09-16

国家自然科学基金项目(51704115)；湖南省自然科学基金项目(2017JJ3099)；湖南省科技计划项目(2016TP1021)；湖南省教育厅科学研究项目(16C0723)

王海星(1990—)，男，讲师，硕士，研究方向：汽车测试技术。

欧先锋(1983—)，男，讲师，博士，研究方向：图像处理/视频压缩编码及传输，电子邮箱：ouxf@hnist.edu.cn。

U464.32，U462

A

2095-5383(2017)04-0027-05