基于电弧模型的电力输电线路早期故障研究
程玉双 崔博文,2 许奇歆,2
(1.集美大学轮机工程学院 2.福建省船舶与海洋工程重点实验室)
基于电弧模型的电力输电线路早期故障研究
程玉双1崔博文1,2许奇歆1,2
(1.集美大学轮机工程学院 2.福建省船舶与海洋工程重点实验室)
本文根据电力系统输电线路早期故障与间歇性电弧故障输出特性的相似性,通过搭建间歇性电弧故障模型来模拟电力系统输电线路的早期故障。应用Matlab搭建电弧电阻模型,同时,在此基础上搭建一个简单的电力系统模型,对输电线路早期故障的各影响因素响应输出状态进行仿真模拟,探究输电线路早期故障的决定因素。
电力输电线路;电弧电阻模型;Matlab仿真;故障分析
0 引言
电能作为最重要的终端能源,同时随着我国工业化进程快速推进,各行业用电需求不断增加,对电力系统的稳定性也提出了更高的要求。电力系统由发电、变电、输电、配电、用电设备或系统组成,为保证用电端得到持续稳定的电力供应,要求电力系统的各个环节都要始终保持无故障运行。
电力系统输电线路上的早期故障是线路绝缘层老化的结果。输电线路及其交接处在外部环境中,受到风吹、日晒以及温度、湿度不断变化的影响,同时也不可避免地受到制造工艺、材质及线路施工的影响,使得绝缘材质老化,进而产生电弧,造成漏放电等早期线路故障[1]。电力系统输电线路的早期故障一般发生在电压峰值附近。线路某一位置开始出现早期故障之后,该故障会反复出现,随着线路绝缘材质老化程度加剧,最终会导致绝缘失效,发生短路故障,造成严重后果[2]。由此看来,加强对电力输电线路早期故障的检测,做好线路故障的预防工作,对保障电力系统的持续稳定安全运行具有重要意义。本文将利用间歇性电弧模型来模拟电力输电线路早期故障,通过仿真结果的分析来探究影响线路早期故障的决定性因素。
1 间歇性电弧的数学模型
电弧具有时变性和非线性的特性,而且电弧电压波形近似于方波,本文搭建的电弧的数学模型能比较好地反映电弧的以上特性[3,4]。电弧模型的推导过程如下:

式中,G为稳定电弧电导;g为瞬时电弧电导;τ为时间常数;iarc为瞬时电弧电流;ust为静态电弧电压;r0为电弧电阻;u0为电弧电压特征;larc为电弧长度。
谐振接地系统中的电流电弧参数由电弧伸展率决定:

式中,elongspd为电弧伸展率;l0为初始电弧长度,l0数值可通过测量获得;vth为初始瞬时电压;vmax为峰值电压。
仿真前将时间常数定义为:

式中,τ0表示初始时间常数;a为系数,为负值,现取值为-4,电弧长度的函数表达式为:
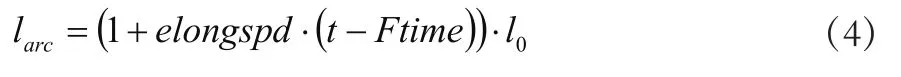
式中,larc为t时刻电弧长度;t为仿真时间;Ftime为电弧发生的初始时刻。
2 建立早期故障的电阻模型
电力输电线路的早期故障一般会伴随电弧产生,故障电阻具有非线性和时变性,由固定电阻和电弧电阻接地来构造电力输电线路导体模型[5]。该模型中电弧电阻rarc与固定电阻r串联组成早期故障电阻R=r+rarc,其中,电弧电阻由时间常数τ0、电弧伸展率elongspd以及电弧初始长度l0三个参数决定。早期故障模块的构造如图1所示,根据式(1)~(4)并用Matlab搭建的电弧电阻数学模型如图2所示。
3 仿真研究和故障分析
图3为接入早期故障模块后所搭建的简单电力系统模型,仿真分析研究固定电阻r、时间常数τ0、电弧伸展率elongspd以及电弧初始长度l0对早期故障模块的影响[6-8]。

图1 早期故障模块
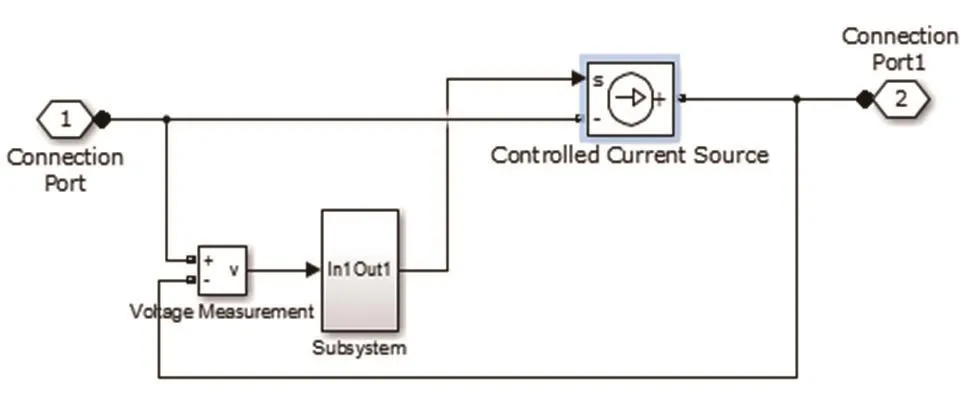
图2 电弧电阻模型
因为电弧伸展率elongspd决定于瞬时电压vth和峰值电压vmax的比值以及初始长度l0,所以为简便起见,设cosβ=vth/vmax,同时设线路故障相为A相,依次改变r、τ0、elongspd、l0的取值,进行仿真并分析如下。
(1)改变串联固定电阻r

图3 电力系统模型
设τ0=0.1ms,l0=0.1m,cosβ=1,计算得elongspd=1.75m/ms,r的变化范围0.01~200,取10组数据,分析比较故障电流峰值Imax和故障电流峰值增加量△Imax,如表1所示。图4、图5横轴表示固定电阻r,纵轴分别表示Imax和△Imax。从图中可明显看出,随着r增大,Imax和△Imax逐渐减小。当0.01≤r≤60时,二者快速下降;当r≥100时,二者几乎不再下降。Imax和△Imax的下降率分别为39.3%和99.8%,由此可判断,固定电阻r对早期故障电流有决定性影响。
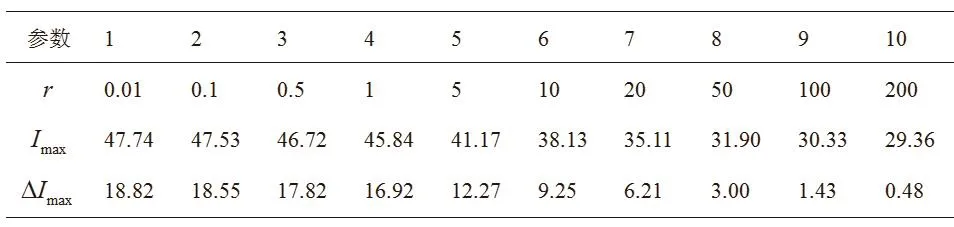
表1 对参数r赋值及计算结果

图4 电流峰值Imax变化图

图5 故障电流峰值增加量△Imax变化图
(2)改变时间常数τ0
设l0=0.1m,cosβ=1,取r=0.1,得elongspd=1.75m/ms,τ0的变化范围0.01~200ms,取10组数据,分析比较故障电流峰值Imax和故障电流峰值增加量△Imax,如表2所示。图6、图7横轴表示时间常数τ0,纵轴分别表示Imax和△Imax。从图中可明显看出,随着r增大,Imax和△Imax逐渐减小。Imax和△Imax的下降率分别为13%和33%,由此可判断,固定电阻τ0对早期故障电流的影响比较小。

表2 对参数τ0赋值及计算结果
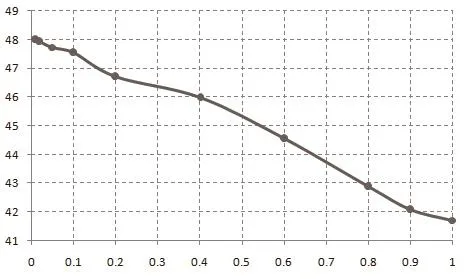
图6 电流峰值Imax变化图

图7 故障电流峰值增加量△Imax变化图
(3)改变电弧伸展率elongspd
设l0=0.1m,τ0=0.1ms,取r=0.1,cosβ的变化范围为0.01~1,elongspd的变化范围为3.456~1.75m/ms,取10组数据,分析比较故障电流峰值Imax和故障电流峰值增加量△Imax,如表3所示。图8、图9横轴表示电弧伸展率elongspd,纵轴分别表示Imax和△Imax。从图中可明显看出,随着r增大,Imax和△Imax逐渐增大。Imax和△Imax的下降率分别为3.55%和8.84%,由此可判断,固定电阻elongspd对早期故障电流的影响较小。
(4)改变初始长度l0
设cosβ=0.1,τ0=0.1ms,取r=0.1,l0的变化范围0.01~1ms,elongspd的 变 化 范 围 为 0.175~17.55m/ms, 取 10组 数据,分析比较故障电流峰值Imax和故障电流峰值增加量△Imax,如表4所示。图10、图11横轴表示电弧初始长度l0,纵轴分别表示Imax和△Imax。从图中可明显看出,随着r增大,Imax和△Imax逐渐减小。Imax和△Imax的下降率分别为45.5%和99.4%,由此可判断,初始长度l0对早期故障电流有决定性影响。

表3 对参数elongspd赋值及计算结果

图8 电流峰值Imax变化图

图10 电流峰值Imax变化图
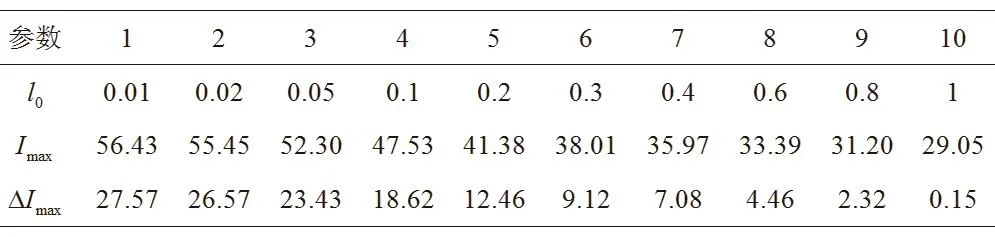
表4 对参数l0赋值及计算结果

图9 故障电流峰值增加量△Imax变化图

图11 故障电流峰值增加量△Imax变化图
4 结束语
根据电力系统输电线路早期故障与间歇性电弧故障输出特性的相似性,利用MATLAB搭建间歇性电弧故障模型来模拟电力系统输电线路的早期故障,同时搭建接入早期故障模块的简单电力系统来进行仿真研究,分析仿真结果发现早期故障模块中的固定电阻和初始电弧长度对早期故障电流有决定性影响,同时也验证了本文研究方法的可行性。
[1] 毛晓东. 电力系统故障诊断应用技术研究[D]. 哈尔滨:哈尔滨工程大学, 2009.
[2] 刘晓明, 赵洋. 基于多特征融合的交流系统串联电弧故障诊断[J].电网技术, 2014, 38(3): 795-800.
[3] 刘晓明, 赵洋. 基于小波变换的交流系统串联电弧故障诊断[J]. 电工技术学报, 2014,29(1):10-16.
[4] Hirofumi Akagi,Edson Hirokazu Watanabe. Instantaneous Power Theory and Applications to Power Conditioning[M]. IEEE Press—Wiley InterScience,2007.
[5] 许奇歆. 基于马尔科夫链的船舶输电系统短路故障预测方法研究[D].厦门:集美大学,2017.
[6] S.Herraiz, V.A.Barrera. Estimation of Zero-Sequence Impendance of Undergrounds Cables for Single-Phase Foult Location in Distribution Systems with Electric Arc[J]. IEEE, 2009(7):105-108.
[7] 许晔, 郭谋发, 陈彬等. 配电网单相接地电弧建模及仿真分析研究[J].电力系统保护与控制,2015,43(7):57-63.
2017-07-05)

