MATLAB图像处理在线性代数教学中的应用

王 兰 朱 翔

(无锡职业技术学院 基础课部，江苏 无锡 214121)

MATLAB图像处理在线性代数教学中的应用

王 兰 朱 翔

(无锡职业技术学院 基础课部，江苏 无锡 214121)

基于图像处理问题与线性代数理论的密切关系，文章通过几个矩阵运算的教学实例，探讨如何将MATLAB图像处理应用到高职院校线性代数的课堂教学中。该做法将理论与应用相结合，有助于学生对理论知识的直观认识，增强其应用意识，提高教学效率,符合高职教育的特点与要求。

高职院校； 课堂教学； 线性代数； MATLAB； 图像处理

线性代数，作为高职院校理工科各专业及经济管理等专业的一门基础必修课，广泛应用于自然科学和社会科学的诸多领域[1]。然而线性代数又是一门抽象性较强的课程。以往的课堂教学，因为辅助工具的限制，主要讲授原理，偏重理论推导。计算方面因为心手口演算的局限性，矩阵运算往往不超过四阶的运算。教学过程中，学生们即使再努力学习，也只能掌握初步的计算，无法将知识拓展开，课程的学习目的不能够完全实现。这种教学模式既脱离了高职院校生源实际，也与高职教育的特点相违背，更无法让学生在以后的工作中结合工作实践灵活运用所学知识。

近年来，由于计算机技术的急速发展和广泛普及，计算机辅助教学得以发展和应用。大量的优秀数学软件的研发，如MATLAB、Maple、Mathematica、MathCAD等，不仅为工业、农业等产业领域的应用提供了便利，也为数学课堂教学提供了新思路。其中MATLAB因其使用方便，可视化编程等优点脱颖而出，出现在越来越多的课堂教学当中[2-5]。文献2主要通过构造矩阵例子来说明软件在教学中的作用。文献3和文献4介绍了一些线性代数的基本知识点如何利用MATLAB来实现，具有一定的教学参考价值。

然而并没有相关的前期研究探讨过MATLAB图像处理功能在该课程教学过程中的应用。而数字图像学、计算机图形学、图像处理、图像识别等无不基于线性代数这门课程[6]。其中,例如去噪、特征提取、降维等技巧均来自线性代数。因此，教学过程，尤其是高职工科专业的教学过程中，图像处理问题顺理成章应当成为线性代数的重要应用案例。

随着即时通讯工具和无线技术的发展，QQ、微信等成为当代大学生必备的手机应用软件。表情包、头像、自拍照等图片文件几乎成为每个学生的“必修课”，图像处理小工具也成为部分学生手机或者电脑的必装软件。 因为是现实生活中常用软件，所以他们能够非常主动地自我学习AB,而且学习效果非常好。而MATLAB是近几年来国际上处理图像问题使用最为广泛的优秀工具之一，因此对于学生更有吸引力。

基于上述探讨，本文将以矩阵及其运算教学为例，探讨MATLAB图像处理功能如何在线性代数教学中发挥辅助作用，用以提高教学效果，实现教学目标。

1 矩阵概念引入的辅助教学设计

矩阵是线性代数中一个基本且重要的概念。笔者通过一个MATLAB图像处理程序，与学生们进行课堂互动，调动了学生的学习积极性。

课前，教师要求学生们通过预习了解矩阵的概念，并准备好一张具有面部的图片。课堂上，首先让学生们上传事先准备好的图片，然后老师利用MATLAB程序对学生们上传的图片进行准确的面部定位，用红色框框出(见图1)，让学生一下子产生好奇心，然后告知学生该程序正是大量运用了矩阵的方法有效完成目标，调动了学生学习的积极性和目的性。

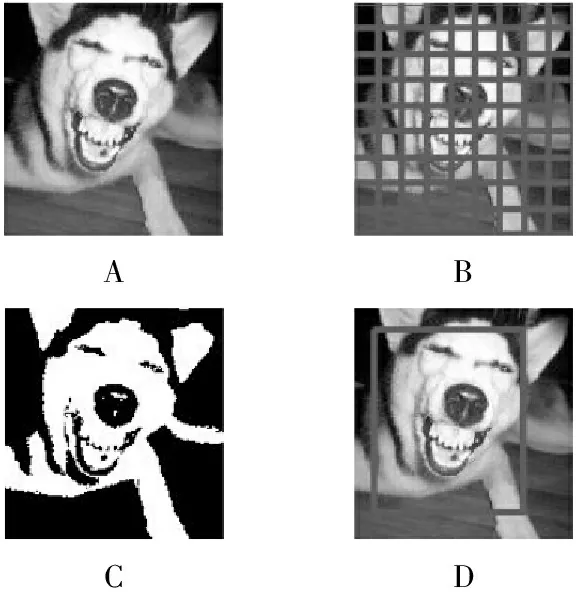
ABCD

A.原图像;B.网格标记图像;C.二值图像;D.标记图像

图1面部定位结果

2 矩阵加法辅助教学设计

矩阵加法定义参见文献7第六章第二节定义1，只有当两个矩阵是同型(行数、列数都相同)矩阵时，才能进行加法运算。调用函数imadd实现图像的加法,调用格式如表1所示。

表1 函数imadd调用格式和说明表

运行结果如图2所示，图像A加上图像B得图像C;图像B加上A得图像D;图像C和D的尺寸与A和B相同;图像C和D相同，但不同于图像A和图像B。

ABCD

A.原图像;B.原图像;C.图像A加图像B;D.图像B加图像A

图2图像加法的结果

图像的加法运算和矩阵的加法运算规则相同,都是对应位置相加。他们的运算规律也保持一致,都满足结合律。学生可以通过图像运算结果去巩固课上所学的矩阵加法运算。所以该部分教学设计为学生理解和掌握矩阵加法运算以及性质提供直观表达。

3 矩阵数乘辅助教学设计

矩阵数乘定义参见文献7第六章第二节定义2。调用函数immultiply实现图像乘法,调用格式如表2所示。

表2 函数immultiply调用格式和说明表

数乘运行结果如图3所示。此时B表示对A图像进行亮度调整，λ代表调节倍数。图中分别展示了λ=2，5,10对应的图像。与矩阵的数乘运算结合，矩阵数乘是使得矩阵的每一个元素都扩大λ倍。

ABCD

A.原图;B.表示增亮2倍;C.增亮5倍;D.表示增亮10倍

图3图像数乘的结果

该部分教学设计,通过图像亮度的改变来引起学生对矩阵数乘概念的兴趣,加深学生对该运算规则和性质的理解。

4 矩阵乘法辅助教学设计

矩阵乘法定义参见文献7第六章第二节定义3，由定义可知当且仅当左边矩阵A的列数与右边矩阵B的行数相等时，乘积AB才有意义。

调用函数mtimes实现Matlab中矩阵相乘。

表3 函数mtimes调用格式和说明

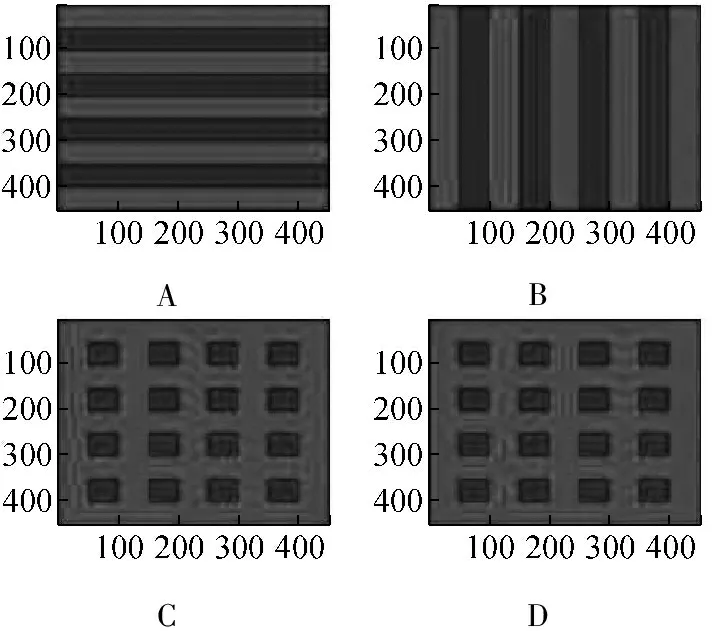
图4给出进行乘法运算的矩阵的图像表示。C表示矩阵a乘以矩阵b所得矩阵c对应的图像,D表示矩阵a乘以矩阵b所得矩阵d对应的图像。C和D是不同的，契合了矩阵乘法不满足交换律。图像的条纹格式，与矩阵乘法定义中，第一个矩阵的行乘以第二个矩阵的列相匹配。

该部分教学设计是利用MATLAB将矩阵A,B以及乘法运算所得到的矩阵C,D变成图像展示出来,让学生对于矩阵以及矩阵乘法运算结果有个直观的认识。最后通过对图像的观察,巩固矩阵乘法运算的规则。

为加深学生对矩阵乘法的理解，突出矩阵乘法与线性变换的联系，笔者通过矩阵乘法编写的Matlab程序对一张图片进行了若干种变换。

利用Matlab软件生成GUI界面，如图5、图6所示。图5中，左乘二阶变换矩阵A=[2 1;0 2]，图像发生剪切变换;图6中，左乘二阶旋转变换矩阵,其中R=45度，图像发生对应度数旋转。原图以及变换图如图7所示。

ABCD

A.矩阵a对应的图像;B.矩阵b对应的图像;C.矩阵a乘以矩阵b所得矩阵对应的图像;D.矩阵a乘以矩阵b所得矩阵对应的图像

图4图像乘法的结果

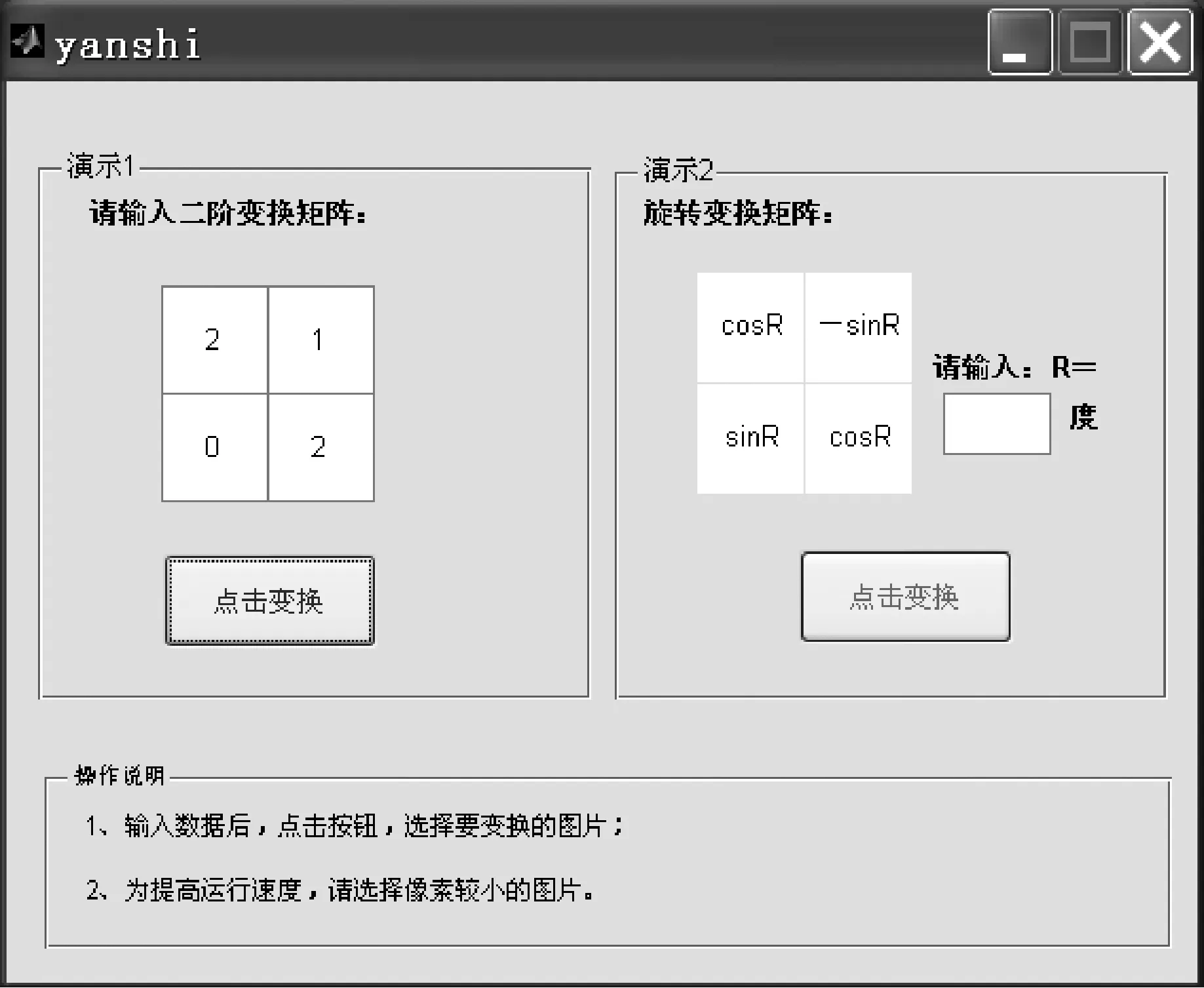
图5 左乘二阶剪切变换矩阵GUI界面

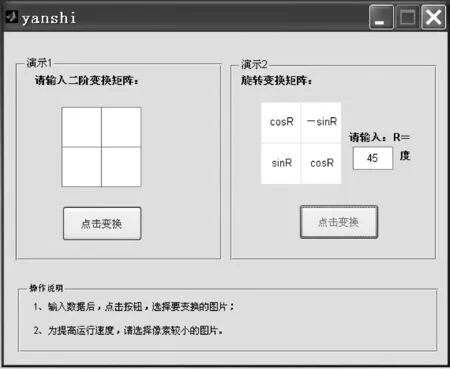
图6 左乘二阶旋转变换矩阵GUI界面

5 方阵的逆辅助教学设计

逆矩阵的概念参见文献7第六章第四节定义1。调用函数imdivide展示矩阵逆的概念和性质，图像除法运算用于校正成像设备的非线性影响。

ABC

A.原图;B.经过剪切变换的图像;C.旋转变换图

图8给出图像除法运算结果。在此,通过思考发现,矩阵的求逆只有方阵的时候才可以运算。而图像的除法并不完全一样,即图A,B并不为正方形。

该部分教学设计,引导学生去思考图像的除法和方阵的逆运算之间的不同点,激发学生发现规律总结规律的兴趣和能力,从而提高学生的数学综合素质。

ABCD

A.原图像；B.原图像;C.图像A除以图像B;D.图像B除以图像A

图8图像除法的结果

6 总结

本文通过MATLAB软件对图像的处理演示，一方面将抽象的理论知识形象直观地表示出来，加深了学生对理论知识的理解;另一方面，给出了线性代数知识的应用案例，增强了学生的应用意识;再者，因为与身边具体问题相结合，调动了学生学习这门课程的积极性。据课堂实践结果统计，全班一共65位同学，共有57位同学发来78张图片，大大提高了课堂的参与度。

虽然MATLAB等一系列数学软件可以在课堂上发挥重要作用，可是它们并不能全部展示数学课程中的全部内容。所以MATLAB软体只能用来帮助我们更好地实现教学效果，并不能绝对取代教师在课堂上的理论讲解。

[1] 同济大学数学系.工程数学线性代数[M].北京：高等教育出版社,2011.

[2] 高淑萍,孙群,杨威,等.线性代数课程MATLAB实验内容的教学与研究[J].中国电子教育,2007(4):59-62.

[3] 丁小星.浅谈MATLAB软件在线性代数教学中的应用[J].中国教育技术装备,2014(4):92-95.

[4] 樊帆,张欣.MATLAB在线性代数教学中的应用[J].教育,2016(9):146-146.

[5] 孙蕾.基于MATLAB软件的“独立学院"线性代数教学改革研究[J].江苏科技信息, 2016 (35):41-43.

[6] 赵海滨.MATLAB应用大全[M].北京：清华大学出版社,2016.

[7] 朱翔,傅小波.应用数学(下册)[M].北京：高等教育出版社，2015.

ApplicationofMATLABImageProcessinginLinearAlgebraTeaching

WANGLan,ZHUXiang

(Division of General Courses，Wuxi Institute of Technology, Wuxi 214121, China)

Image processing is closely related to the theory of linear algebra. This paper studies how to use Matlab image processing in linear algebra classroom teaching in higher vocational colleges based on several examples of matrix operation. This method effectively combines theory with application, and helps students to understand the theoretical knowledge intuitively and enhances their application consciousness. Therefore, it is more in line with the characteristics and requirements of higher vocational education.

higher vocational colleges； classroom teaching； linear algebra； MATLAB； image processing

2017-09-25

王兰(1983— )，女，江苏邳州人，讲师，博士，研究方向：应用数学;

朱翔(1981— ),男,江苏高邮人,副教授,研究方向:高职数学教学,模糊代数。

10.13750/j.cnki.issn.1671-7880.2017.06.011

G 710

A

1671-7880(2017)06-0038-04

责任编辑俞林