数学作文：快乐学习的自平台

【摘 要】数学作文是学生表达数学学习主张和数学发现的平台。它利于学生将学习思维延伸到课外，为学生的奇思妙想提供交流平台，给学生质疑、展示提供分享渠道。它保证了学习过程的愉悦，也让学生享受到学习结果的成就感。

【关键词】数学作文；快乐学习；创新思维

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2017）67-0011-04

【作者简介】戴志鸿，南京师范大学附属中学树人学校（南京，210036）教研处主任，高级教师。

数学学习，曾是许多人多年挥之不去的噩梦。不少名人都多次提到上学时，数学学习过程中的纠结、困惑和痛苦，引起一群人的共鸣。究其原因，数学学习过程中，学生缺少交流讨论的平台，没有机会表达自己的数学主张、数学发现，无法满足自己的探究欲，体验不到成就感，从而生成负面的学习体验。为解决学习困境，提升学生学习的幸福感，数学作文顺势而生。学生在数学作文中，探讨数学问题、交流数学观念，感受数学的美丽，分享数学学习的成就，体验学习输出的快乐。数学作文，丰富了传统的数学学习模式，填补了学习过程的输出渠道，成為学生快乐学习的自平台。

一、延伸数学思维的时空，满足学生的探究欲

课堂教学中，学生常常会生成一些奇思妙想，或者有对一些问题的探讨，但因教学进度或教学设计的约束，学生常常浅尝辄止，意犹未尽。课堂教学，无法满足学生的探究欲和好奇心。两周一次的数学作文，给学生充分的思考时间、充足的研究空间，有效弥补了课堂教学的不足，极大地满足了学生的探究欲。数学作文中，学生能充分阐述对数学问题的研究、探索、发现及困惑。通过数学作文，教师也可以清晰地了解学生思考的深度和广度，关注学生数学学习的水平，掌握学习动态，洞悉学习心理，全面评价学生数学学习的过程。

案例1：关于增根（作者：刘语欣）。

1.增根的产生。

在解分式方程时我们常常会遇到一种情况，即得到的解是原方程的增根，此时方程无解。我们知道，判断得到的解是否是增根的方法是：将解代入分母看分母的值是否为0，由此便可判断出增根的产生原因。

……

2.增根究竟是什么。

……

经过上面的三个步骤，得到一个矛盾等式，便可得知原方程无解。增根其实就是在第2步的时候让左右两边都乘0，把原来的矛盾式变为了等式，从而产生了增根。

课上戴老师让我们写一个解出的答案为增根的分式方程，利用这个原理可以很快写出。

3.有关增根的习题。

……

到这一步时，依照解整式方程的方法 （即关于x的方程ax=b，当a=0且b≠0时方程无解）。我们可以很快求出t=-1，但这时，必须注意整式方程与分式的差别，即增根，所以必须再讨论。

……

仔细检验，全面考虑，关于分式方程的增根问题其实很简单。

解分式方程，必须要进行验根，这是解分式方程和整式方程的最大区别。教学中可能会强调怎样验根，而对增根的产生原因常常一句话带过。对学生而言，没有理解为什么会产生增根，验根的重要性也就没有体会。如果仅仅靠扣分、订正来强化学生的计算操作训练，只能培养出机械解题的工具，对学生的数学素养提升没有任何意义。刘语欣同学自己对分式方程的增根进行了三个方面的探究，明白了怎么会产生增根、怎样构造有增根的分式方程，方程有增根与方程无解的关系。这三个问题反映了她对分式方程的思考深度和宽度。能进行这样的总结和研究，足以说明她对分式方程增根的理解已超越课标的层次要求。

二、丰富学习输出的形式，满足学生的多元化发展需求

学生的多元化发展，需要不同形式的学习方法，多样的输出形式。中学生学习幸福感的愉悦，既包括感官上的满足，也包括对认知结果的愉悦，感官知觉通道的学习兴致和指向认知通道的学习效能，都是学生学习幸福感的因子。（孙小红，2017）数学作文，有机融合了数学学习、反思、探究、对话、讨论、交流、分享等方面的功能，满足了学生认知通道多元化发展的需求。

案例2：数学中物极必反的奥秘。（作者：朱亦陈）

“物极必反”是个成语，和“乐极生悲”的意思差不多。在数学中，也存在这样的道理。

上个星期，在学习数轴与绝对值时，老师出了这样一道题目：比较a与的大小。我觉得，这道题给二、三年级的同学做，会说是a>，因为3>，4>，可是，事实上，这道题可没这么简单。

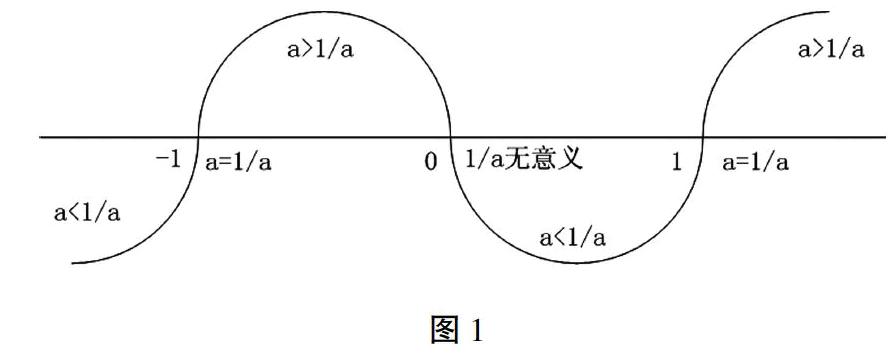
首先，这道题应该分类讨论，先找特殊点：1= ，-1=，无意义。那么特殊点便是1，0，-1。

画个数轴，我惊奇地发现：

先是大于；到了“1”，变成小于；到了“0”，又变成大于；到了“-1”，再变成小于。这是怎么回事？数学中竟然神奇地蕴含着“物极必反”的哲理？！

我突然想到了“负负得正”。的确，“负负得正”也是“物极必反”。

看来，数学中也蕴涵许多道理啊！

初中数学中，分类讨论是很重要的方法之一。许多学生经过多次训练，对一些问题能进行分类讨论来研究。朱亦陈同学不仅学会分类，在分类中还发现有趣的规律，并对此展开归纳，得出“物极必反”的道理。数学中蕴涵的哲理，就这样被善于思考的学生捕捉到了。这样一个“生动活泼、富有个性的”学习过程，在数学写作中展现得淋漓尽致。可以想象，当学生经过独立思考，猛然间顿悟出一个道理，其间的愉快一定妙不可言。endprint

三、拓宽书本内容的边界，满足学生的求解欲

数学学习的过程中，学生常常会冒出一些思维火花，也有一些困惑或不明白，限于教师课堂教学的主导性、书本内容的阶段性，学生常失去进一步探究和质疑的机会。他们心中萌动的数学之火，急需寻求解答，与别人分享交流。数学作文，给学生提供阐述发现或思考的平台，满足他们的求解欲。

案例3：关于在数轴上表示无理数。（作者：姚舜）

学数轴一课时，戴老师教我们如何在数轴上表示无理数，例如。如图2，=，再用圆规把点转到数轴上，点F表示的数是。

这个方法很神奇，我突然想到一个问题：那呢？怎样在数轴上用直尺和圆规表示。因为不能表示成（a，b为整数）。如果用小数不就有太多情况了？那也太乱了吧！有没有其他公式或方法呢？

经过反复思考，我想到了这样一种方法表示，如图3。

因为=，在的点上画一条长为单位长度1的線段，与数轴垂直，连接OB，并用圆规把B点转到数轴上就表示出了。

于是，我得到一个方法：=（n为正整数），这样可以算出任何正整数的开方，也可以在数轴上画出相应的点。

用直尺和圆规在数轴上表示无理数，是数形结合的一个典型例子。熟练借助勾股定理，巧妙构造直角三角形，是解决这类问题的关键。课本中，只要求学生掌握简单的作法。姚舜同学学习了在数轴上表示方法后，惊叹这个方法的“神奇”，激发他产生“怎样表示？”的疑问，并进行了探究。课本方法的迁移，看出他对数学问题的灵敏性、解决问题的创新性。字里行间，能感受到学生提出问题，自主探索后的喜悦。

四、促进学习过程的完整，满足学生学习的流畅感和成就感

数学教材中安排了多个“数学实验室”，由于内容贴近学生实际，富于趣味性和合作性，深受学生喜欢。开展数学活动，学生参与度高，形式上比较热闹，气氛也较融洽。学生在数学活动中，与同学合作交流、研究比赛策略、承受困惑失败，分享成功喜悦。这种经历，学生记忆深刻，感触很多。活动结束后，学生用文字描述数学活动中难忘的细节，或印象深刻的环节，记录自己的思考和困惑，回味活动过程中的失败和成功，数学作文，弥补了传统学习中的虎头蛇尾，促进整个学习过程的完整性，提升了学生学习时的流畅感和成就感。

案例4：制作扑克牌。（作者：胡文琦）

前不久的那节数学课是我们的第一次活动课。老师发给我们几张纸，让我们四个人一组合作做一副扑克牌。我被分到了做“梅花”花色的13张牌。首先，裁纸就是一项精细活儿。我们把一张纸经过对折成16块区域，然后拿剪刀裁剪，但我发现用剪刀裁简直就像“狗啃”的一样，边缘歪歪扭扭，不如拿把尺子和裁纸刀合作裁得整齐。在各张牌上除了写点数和花色以外，还要在中间画上几个花色图案，而这又牵涉到怎么“布局”和研究它们的正反。比如“8”就是21212排列，而不是2×4排列。经过好一番不懈努力，我们终于完工了。本来以为很简单的事情，其实也很有讲究呢！老师说，活动课是为了锻炼我们的动手能力的。我觉得活动课很有意义，不仅有趣，让我们从繁忙的学习中“抽出身”来放松放松，也能锻炼动手能力、思考的能力和审美。我喜欢这样的活动！

“纸上得来终觉浅，绝知此事要躬行。”不亲手制作扑克牌，怎么会发现扑克牌中有“写法、图案、正反”这么多奥妙。数学活动中，方案设计、分工合作、动手操作都是客观存在的问题，这些矛盾和任务，需要学生的智慧，更需要学生的观察、实验和自我纠错。活动结束，思考并没有停止，回头再去看看，细细品味，成就感油然而生。

五、提供数学研究平台，满足学生的创新欲和展示欲

学生不乏好奇心、探究欲，他们的眼中有成人不懂的世界。培养学生发展核心素养中的“学会学习、科学精神、实践创新”，需要给学生一个载体，一个展示的平台。数学作文，引导学生去思考、发现与分享。

案例5：带上计步器去散步。（作者：徐天逸）

……

先将计步器清零，然后到楼下先走100步试试。我试了一下，看计步器显示153步。这怎么回事，又走100步（心里默数的），计步器显示310步。我约莫算了一下，计步器的步数与实际步数比约为3∶2。这是因为计步器的原理特殊。它是按振动的幅度来算的。如果标准振动的数值是x，那么我每走一步的振幅大约是1.5x。由于我的步伐比较均匀，由此我们找到了窍门。

当计步器显示3000步时，我们大约走了1000米。这是我们得到的结论。我兴奋得大叫起来。为了数据的严谨，我又实际测算了两次。两次结果如下：

……

今天可以说，得出了一些结论：看似不怎么准的计步器，其中一定也有它的奥秘。数学是一个严谨的学科，它一定要通过计算、推理、实验得来。一个结果的背后凝结了多少汗水，我只是验证一个结论，竟如此困难。以至于我满头大汗，但数学又是奇妙的，两个毫不相干的事物——计步器、距离，竟有这么大的联系……

知识的迁移、能力的提升在不知不觉中进行，学生对生活中的一个问题、一个发现都会及时写下来，与老师交流，跟同学分享。借助学习行为，学会领悟，学会发现自我。这种主动学习，正是学生快乐学习的基础和本源。

总之，数学作文，丰富了数学学习形式，激发了学生的数学学习兴趣，满足了学生认知需求，开辟了一条师生心灵交流的通道，有利于师生间的情感交流，成为学生学习的一片快乐沃土。正如学生所说：“写数学作文其实就是一个探究的过程，总结的过程，因此它能让我们的思维变得有条理、思想变得有深度，也能让我们充分体验到数学的魅力，真正喜欢学习数学、喜欢探究和思考。数学写作，让我们多了一份交流的能力。”