基于CEEMDAN与量子粒子支持向量机的电力负荷组合预测*

贾逸伦，龚庆武，李俊雄，占劲松

（武汉大学 电气工程学院，武汉 430072）

0 引 言

负荷预测在现代电力系统运行管理中占有重要地位，对其精确预测是保证电力系统稳定调度与计划的重要基础。目前多种方法已应用于此方向，如神经网络模型，支持向量机（SVM）模型，时间序列（ARMA）方法，卡尔曼滤波等方法［1-3］。而在实际操作中，由于负荷信号往往具有复杂的时频分布特性与动态机理较强的非线性特征，故单一预测方法往往不能兼顾不同时间尺度的变化特征。而使用前置分解能提取出非稳态负荷信号中不同时间尺度的信息，并用统计学方法分别对其进行预测，故该类方法往往能改善预测效果［4-5］。经验模态分解（Empirical Mode Decomposition，EMD）是近年黄锷提出的一种自适应处理非线性与非稳态信号方法，可以依次分解信号中的不同尺度信息。相比小波分析等其他分解方法，EMD克服了需要人为经验选择小波基函数与分解层数等不足，减少了主观因素对结果的影响。然而其自身仍存在着一些不足，如信号采样率设置、分解过程的循环终止条件设置、样条插值边界效应处理等问题。其中，分解产生的模态混叠现象，会对后续的预测结果产生较强的影响。针对模态混叠问题，Huang提出集合经验模态分解方法（EEMD）［6］，通过添加均匀分布的高斯白噪声，并利用多次平均计算使零均值白噪声互相抵消，从而消除模态混叠现象并消除白噪声［7］。

然而，由于白噪声分布的随机性及集成平均实验次数的有限性，在多尺度分解后，各重构信号仍有一定幅值的噪声残留，使预测的准确性降低，重构误差可以通过增大集成平均计算次数减少，但会增大运算量，提高计算负荷。基于此，本文引入一种新型的添加自适应白噪声的完全集合经验模态分解方法（Complete Ensemble Empirical Mode Decomposition with adaptive noise，CEEMDAN），通过对 EEMD分解过后的各分量进行白噪声分量的叠加抵消，使由噪声产生的重构误差在分解过程中就消失，既保证分解精度，更提高了模态间的分辨率［8］。

在各种单项预测方法中，支持向量机方法由于其转化复杂高维空间，并具有较好的泛化推广能力，避免过学习问题等特点，成为人工智能方法与数据挖掘的新的研究热点。而其中如何确定SVM方法中的不敏感损失系数、惩罚系数与核宽度系数等问题都决定了模型自身的准确性与有效性，故对其更精确与更方便的选择是SVM算法中最重要的问题。本文提出利用量子粒子群算法对该系数进行寻优［9］，并与CEEMDAN方法结合进行组合预测，得到较为精确结果，从而证实了该方法的有效性。

1 EMD、EEMD与CEEMDAN方法

1.1 经验模态分解（EMD）与集合经验模态分解（EEMD）

EMD方法是时间序列处理方法—希尔伯特黄变换（Hilbert-Huang Transform，HHT）方法的核心，其本质是对信号做平稳化处理，得到包含不同时间尺度重构局部特征信号的固有模态分量（Intrinsic Mode Function，IMF），其应满足：（1）序列长度中跨 0点与极值点的数目相等或差1；（2）由局部极大值构成的上包络线与局部极小值构成的下包络线均值为0，即与时间轴对称。原始信号x（t）经EMD分解后可表示为：

式中IMFi（t）为包含时间序列不同尺度分量，r（t）为残余函数，代表信号整体趋势。EMD算法步骤如下：

（1）确定x（t）所有局部极值点，并通过三次样条插值分别连接极大值与极小值点，得到信号的上下包络线Umax（t）与Umin（t），并求出均值，进而得到原始信号与均值的差值h1（t），有：作为最终的IMF。

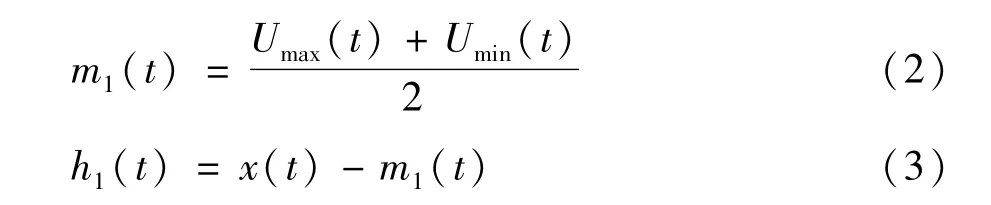
1.2 添加自适应白噪声的完全集合经验模态分解（CEEMDAN）

EEMD方法可以在一定范围内减小模态混叠现象的产生，但由于新加入白噪声序列，在有限次的平均计算后，误差并不会完全抵消，会影响重构序列的准确性，进而影响预测的精度。误差值虽可以通过集成平均次数的增多而减少，但运算量与计算时间又随之大幅增加。基于此现象，本文引入CEEMDAN方法，其在在每次EEMD分解中，由于其添加白噪声nj（t）不同，最终产生的残余信号都不同［10］，即有：

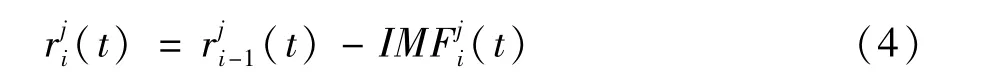
（2）检验h1（t）是否满足 IFM条件，若满足，则有IMF1（t）=h1（t），并从原始信号x（t）中减去IMF1（t）得残余信号r1（t）；如不满足，则将x（t）替换为h1（t），并重复步骤一，直到新的h1k（t）满足条件；

（3）以r1（t）为新的待分解信号，重复上述过程，得到N个IMF分量。当最终残余信号为单调函数或满足变化足够小条件时，迭代终止，EMD分解完成。

EEMD在传统EMD基础上，针对模态混叠问题，引入高斯白噪声辅助进行数据分析，其步骤为：

（1）给原始数据x（t）中加入均值为0，标准差kε为的白噪声序列nj（t），其中，k为白噪声序列幅值系数，ε为序列标准差。一般k取0.01～0.5较适宜，且需多次尝试比较得到更好结果；

（2）将上述混合序列进行EMD分解；

（3）执行 M次步骤（1）、（2），每次加入不同的nj（t）；

（4）取M次分解后所得固有模态分量的均值

定义算子emdi（）为利用EMD算法产生的第i个模态分量，用CEEMDAN方法所得的第个模态分量记为，该方法步骤如下：

（1）与EEMD算法相同，CEEMDAN算法在M次计算中，对原始数据x（t）+p0nj进行分解，其中，参数pi控制着附加噪声与原始信号的信噪比，使其保持在合适范围，则第一个模态分量为：

（2）在下一步分解前，继续引入白噪声信号自我EMD分解的第一阶分量，将其与残余信号组合以消除噪声对原始信号造成的误差，则待分解信号更新为r1（t）+p1emd1（nj（t））。继续用EEMD对第二个模态分量集成平均，可有：

（3）对剩余阶段，继续利用步骤2方式计算残余信号，可得第n+1个模态分量为：

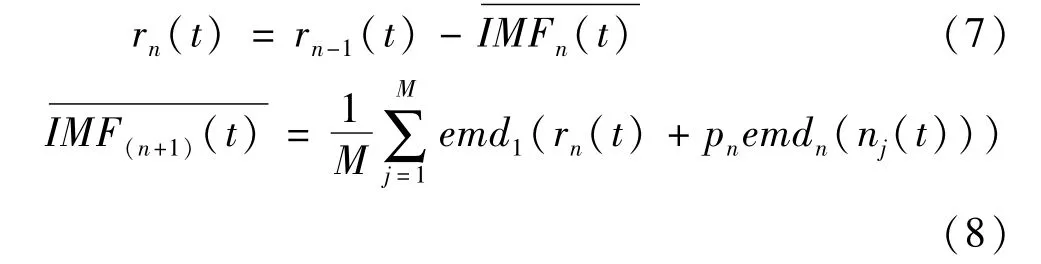
（4）当最终残余信号满足迭代终止条件时，算法终止，设此时有N个最终模态分量，则原始序列可表示为：

利用本文所示改进方法，可消除每阶模态分解后残余信号中由于添加白噪声所产生的误差，从而使分解结果更加精确。

2 量子粒子群支持向量机预测方法

支持向量机方法（SVM）已被证实是一种非常有效且高效的监督学习方法，其以VC维理论与结构风险最小原理为基础，构造分类超平面，将非线性问题映射到高维空间进行线性转化。SVM方法的核心在于其参数的选择，其中不敏感损失系数ν与惩罚系数C控制模型的复杂程度与精度，核宽度系数σ也影响着计算结果与运算量的大小，故对此三系数（C，σ，ν）的选择，是SVM算法中的关键问题。

许多规范的参数寻优方法被应用于支持向量机的参数寻优中，其中粒子群算法凭借其搜索速度快、效率高、算法简单等优势已被大量应用。而针对其容易陷入早熟收敛和局部收敛的缺陷，一些改进措施被提出应用，其中主要两种为带收缩因子的粒子群算法（YSPSO）与带惯性权重的粒子群算法（SPSO）［11］，且后者的性能通常要优于前者。本文采用量子粒子群改进基本算法（Quantum Particle Swarm Optimization，QPSO），并与前两种算法进行对比分析。量子粒子群算法首先由Sun提出，其将粒子群算法理论与量子力学的理论知识相结合，利用量子物理学中的量子运动方式描述粒子的运动，从而保证粒子的运动覆盖整个可行解区域，从而保证搜索到全局最优解［12］。

粒子群算法中粒子运动过程用量子力学来描述时，可以认为粒子群以点qi=（qi，1，qi，2，…，qi，m为吸引势场中心进行运动。吸引势场中心点的坐标可以描述为：

式中j=0，1，…，m，m为粒子维数；φi，j（t）是［0，1］上均匀分布的随机数；pi，j（t）代表粒子经历过的最优位置；pg，j（t）代表种群经历过的最优位置。

量子空间中，使用波函数ψ来描述粒子的状态，波函数的模的平方值代表了粒子出现在空间某一点的概率密度，公式为：

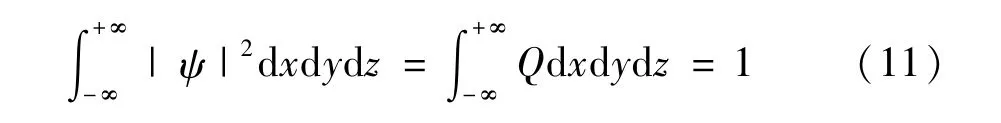
Q表示粒子在当前时刻在点（x，y，z）出现的概率。假设单个粒子在一维空间中运动时，粒子的位置为X。p是粒子的吸引中心，在多维空间中时即为公式（9）中qi，j（t），在p处建立一维δ势阱，通过求解薛定谔方程得到概率密度函数Q，再通过蒙特卡洛随机模拟来测量量子的位置，可得算法的粒子基本进化方程：

式中L是一维势阱的特征长度；u是［0，1］上均匀分布的随机数。在多维空间中的粒子，可对每一维的吸引中心分别建立一维δ势阱进行计算。故求解吸引中心qi，j（t）转化为确定Li，j（t）的值，定义平均最好位置P（t）为粒子群中个体最好位置的平均值，对于m维空间中的n个粒子，平均最好位置为：

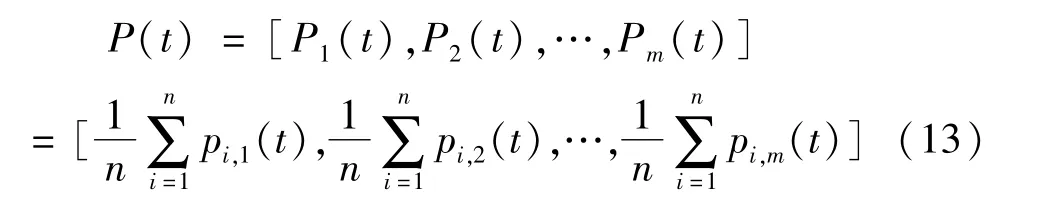
则Li，j（t）值可由下式确定：

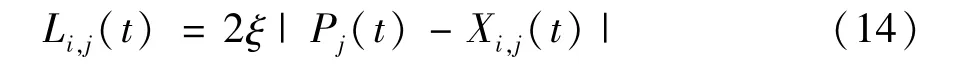
其中，ξ是收缩—扩张系数，也是算法中除了迭代次数和种群规模之外唯一的一个可控制的参数，可以取作一个固定值，也可按一定方式动态变化。带入式（11），得：

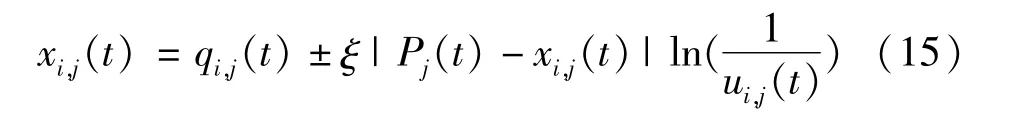
收缩—扩张因子可按式（15）进行变化：

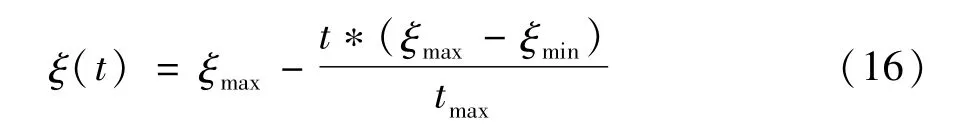
式中ξmax为收缩—扩张因子最大值，ξmin为最小值，tmax为最大迭代次数。根据如上定义，在粒子群算法中，选定上述参数值后，随机初始化中群内所有粒子位置后，利用式（13）计算种群的平均最优位置P（0），计算每个粒子的适应度值，将当前各粒子的适应度值和当前位置储存于粒子最优解pbest中，当前种群的适应度值和当前最优位置储存于种群最优解gbest中。再用式（10）、式（14）、式（15）更新粒子位置与吸引中心后计算新的各粒子间适应度值，并与之前pbest所保存值相比较，取出更优值。在满足终止条件和最大迭代次数后，输出最优解。

3 算例分析

本文以MATLAB作为开发环境，选择中国青海某区域实测负荷输出功率数据为试验样本，该数据以2012年到2013年每隔半小时的电力负荷值为样本，选取每日最大负荷值为采样点，预测2014年1月每日最大负荷值，即进行负荷中期峰值预测。其序列样本如图1所示。

图1 青海某区域两年每日最大负荷序列Fig.1 Daily maximum load series of two years in a certain domain in Qinghai

首先，应用EMD，EEMD与CEEMDAN三种时间序列分解方法，将负荷序列分解为不同时间尺度，比较三种方法优劣。其中加入白噪声幅值系数k=0.2，集成次数M=500。其中，利用CEEMDAN算法所分解不同尺度模态分量如图2所示。

可以看出，IMF1分量是不具有明显周期性变化的随机高频分量，而IMF2则为明显有以星期为单位的周期分量，IMF3到IMF6所表示的时间尺度分量也表现出一定的周期特性，且其每个分量中没有大幅的频率变化，各模态分量也没有重合的频率部分，故其分解的模态中并没有明显的混叠部分。为进一步比较该方法对模态混叠的现象的改进，将EMD，EEMD与CEEMDAN三种时间序列分解方法的Hilbert谱所列如下，为方便观察，仅列出各序列的瞬时频率值，未给出其瞬时幅值：

图2 CEEMDAN算法分解原始序列图Fig.2 Decomposition result of original series using CEEMDAN algorithm

由图3可以看出，在横向时间轴中某些点有着一定程度的聚集，而聚集为一定程度的点则表现为连贯的线，其中每一点表示由EMD方法分解的各IMF瞬时频率值。可以看出，图（a）的各IMF瞬时频率值分开程度不明显，各相邻分量间瞬时频率有着部分重合与混叠部分，尤其在最高频（图中瞬时频率在0.3～0.5部分）变化幅度大，且混乱性高，故可看出其模态混叠问题较为严重。而在图（b）与图（c）中，各IMF分开程度相较图（c）有了提高，能显著看出各分量有了自己一定的频率区域，且在一定范围内变化，各分量间的重叠部分明显减少。相比图（b），图（c）的高频随机分量瞬时频率值明显与其他部分更加分开，说明利用CEEMDAN方法在初始分解高频随机分量后对残余分量补足白噪声的一阶分量起到了明显效果。由图所示，EEMD与CEEMDAN两种方法都有效缓解了模态混叠现象，而CEEMDAN使各分量有了更明显的区分，有着更好的效果。

图4给出了三种方法分解信号后的重构误差，可以看出，在添加500组白噪声后，EEMD分解确实使分解信号的重构误差显著增加，比原始EMD分解高很多量级，而CEEMDAN方法将白噪声在各次分解中分别带入抵消，故其重构误差又降回原来量级，保证了后面的预测结果，验证了该方法的优越性。

图3 三种分解方法Hilbert谱图Fig.3 Hilbert spectrum diagram of three decomposition methods

图4 三种分解方法的重构误差Fig.4 Reconstruction error of three decomposition methods

得到原始信号的各分解值后，本文利用所提出的QPSO—SVM方法进行预测，由于预测值为1月负荷值，故选择两年内11月至12月，1月至2月数据作为训练数据，以预测前7天负荷最大值为输入量，并分别用二进制量1，0区分该日期为工作日还是节假日。使用滚动预测形式，例如用2013年12月25日至31日数据，得到2014年1月1日负荷最大量，然后利用基于得到的预测值再预测1月2日的负荷值，依此类推，直到得到预测的全部结果。

为比较本文所提方法的有效性与优异性，引入EMD-QPSO，EEMD-QPSO，CEEMDAN-YSPSO 与CEEMDAN-SPSO四种算法进行比较，选择三参数向量为（C，σ，ν），粒子群的规模n=20、最大迭代次数tmax=200、取ξmax=1，ξmin=0.5。YSPSO算法中学习因子c1=c2=2.05，收缩因子ξ=0.73，交叉验证折数β=5；SPSO算法中，取c1=c2=2，最大惯性权重wmax=0.9，最小惯性权重wmin=0.4，交叉验证折数β=5；QPSO算法中，对于空间第i个粒子，有：

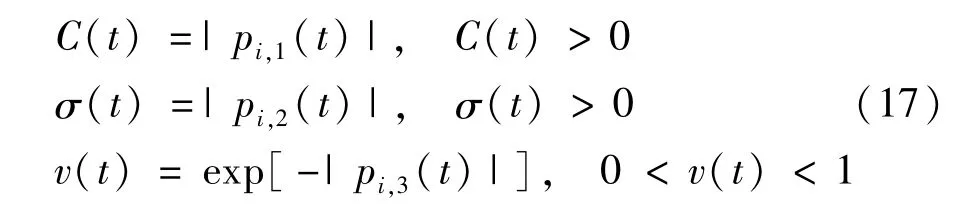
利用所求三向量值带入式（10）～式（15）中进行寻优，并将所求结果带入支持向量机中，最终得到预测结果，并合并各分量预测值，与实际结果数据相对比，其数值比较如图5所示。

图5 不同组合方法预测结果图Fig.5 Forecast result diagram of different combined methods

从图中可以看出，CEEMDAN-QPSO方法的预测值最为接近实际值，CEEMDAN-YSPSO方法由于向量参数的选择不同，得到的预测结果与实际值差距在几种方法中明显较大，而EEMD-QPSO方法由于白噪声的引入，在某些点也有着较高的预测误差，局部效果劣于EMD-QPSO方法，CEEMDAN-SPSO也有着较好的预测效果，但整体精度仍不如CEEMDAN-QPSO。

进一步比较五种方法的结果优劣程度，取其最大相对误差（maximum relative error），最小相对误差（minimum relative error）与平均绝对百分误差（mean absolute percentage error，MAPE）三个数值进行比较，所得结果如表1所示。

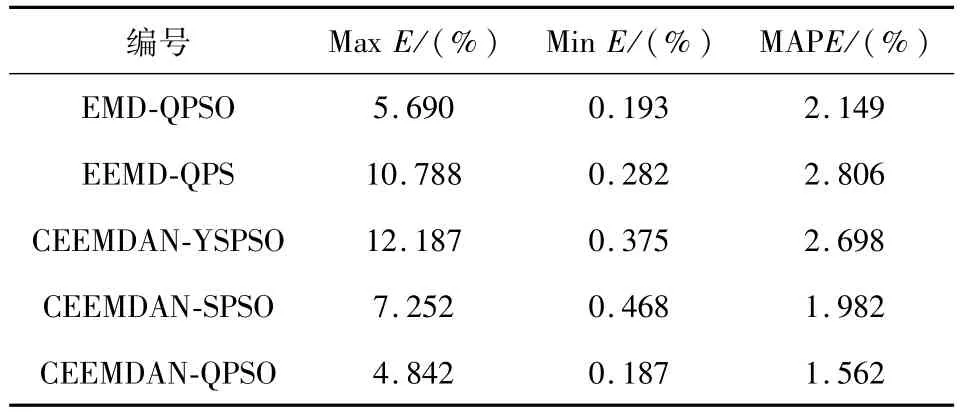
表1 不同组合预测方法性能比较Tab.1 Property comparison of different combined forecasting methods

由表1可看出，由于EEMD方法局部点预测与真实值差距较大，且作用较为明显，使最终MAPE值最大，CEEMDAN-YSPSO方法整体与真实值也有一定距离，虽然CEEMDAN-SPSO方法的最小相对误差值较大，但其整体预测效果与实际值相契合。在五种方法中，本文所提CEEMDAN-QPSO方法在三个指标中，都有着更好的效果，验证了该方法的实际应用性。

4 结束语

本文提出一种基于添加自适应白噪声的完全集合经验模态分解方法与量子粒子支持向量机的预测方法，为电力负荷的预测提供一种新的解决方法。经过与其他方法的实验对比，验证了该方法的准确性与创新性。

其中在预测结果中，本文所提方法有一定创新，但由于EMD方法自身对准确性的要求，需要大量的集成运算，故在运算量的控制与进一步减少预测时间上仍可以继续研究。而在预测中，除了工作日与休息日的区别，对其他可能影响预测结果的因素，如气候等条件的引入，可以作为下一步的研究方向。