基于CEQ（λ）强化学习算法的微电网智能发电控制*

唐捷，张泽宇，程乐峰，张孝顺，余涛

（1.广东电网有限责任公司韶关供电局，广东 韶关 512026；2.华南理工大学 电力学院，广州 510640）

0 引 言

自1998年CERTS提出微电网概念至今，各国学者对微电网展开了深入的研究［1-2］。微电网中包含大量的可再生能源，其出力受环境变化影响很大。这种随机性和间歇性给微电网的控制带来了极大的挑战。尤其当微电网处于孤岛运行模式下，其频率和电压失去了大电网的支撑，受可再生能源波动的影响更为严重。

由于传统PI控制器难以满足微电网复杂的运行工况，基于人工智能算法的智能控制器在孤岛微电网中应用的研究受到关注。模糊控制（Fuzzy Control，FC）、粒子群算法（PSO）、细菌觅食优化（Bacterial Foraging Optimization，BFO）、遗传算法（GA）和传统的梯度下降法（Gradient Descent，GD）等算法被用来对微电网的所有控制参数进行同步优化，实现微电网的自动发电控制（Automatic Generation Control，AGC）［3-10］。上述研究中人工智能算法都是通过调节系统控制参数来实现优化的目的，其本质上仍属于PI控制。笔者曾提出一种集中式的微电网分层AGC控制框架，并采用R（λ）学习算法通过试错寻优，获得最优调度总指令［11］。该控制方法突破了传统的PI控制，通过基于强化学习的AGC控制器直接获得各调频机组的调度指令，实现微电网的智能发电控制。但其在分配过程中采用机组出力组合空间有限的分配因子，使得寻到的调度指令并不一定是最优指令，且在AGC机组调节次数和算法收敛速度上依然存在较大的优化空间。

本文针对孤岛运行时微电网的有功-频率控制问题，提出了全新的基于多智能体CEQ（λ）（Correlated Equilibrium-Q（λ））学习的智能发电控制方法，并在一个包含光伏发电、风力发电、小水电、微型燃气轮机和飞轮储能的微电网LFC模型上进行了仿真。为了展示新算法在孤岛微电网有功-频率控制中的应用效果，本文分别从预学习特性和中长期控制性能两个方面将新算法与传统PI控制和单智能体强化学习控制进行了对比分析。

1 多智能体相关均衡Q（λ）学习

1.1 相关均衡理论

马尔科夫决策过程是指决策者根据每个时刻观察到的状态，从可用的动作集合中选择一个动作做出决策，系统状态的转移是随机的，该随机过程未来发展的概率规律与历史无关。马尔科夫决策过程中，每个智能体在所有智能体的动作概率分布基础上最大化自己的奖励值，由此所形成的动态平衡即为相关均衡。相关均衡的动态描述为：

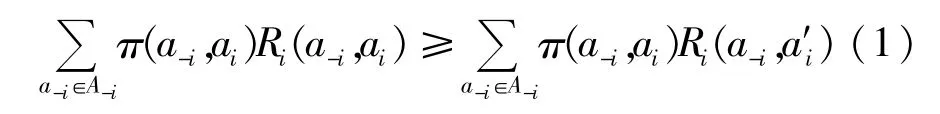
式中ai为满足相关均衡时智能体i的动作，a′i为非均衡状态下智能体i的动作，a-i表示除智能体i其他智能体的动作，A-i=∏j≠i Aj，Ai为智能体i的动作集合，π为均衡策略（即动作概率），Ri为智能体i的立即奖励函数。如果某一策略π对于所有智能体i、所有动作ai、a-i∈Ai（π（ai）＞0）式（1）均成立，该策略即为相关均衡动态平衡点［12-14］。

1.2 CEQ学习算法

强化学习是一种不依赖与模型，基于值函数迭代的单智能体在线学习算法。对策论的研究为多智能体交互提供了可靠的数学框架，从而使得将强化学习与对策论相结合的多智能体学习算法被广泛研究。

CEQ是离散时间马尔科夫决策过程下的一种基于值函数迭代的在线学习和动态优化技术。给定所有智能体i∈N，所有状态s∈S和动作a∈A（s）在时刻t的Q值：；给定均衡策略πt；给定均衡目标函数f；相关均衡条件下，根据马尔科夫对策规则可定义时刻t+1智能体i的动作值函数状态值函数和均衡策略πt+1分别为：

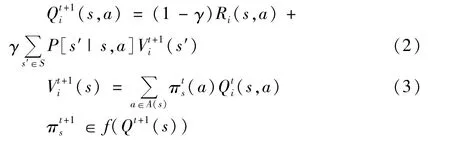
相关均衡策略的线性约束描述为对所有智能体i、所有动作ai、a-i∈Ai（π（ai）＞0）式（4）均成立：

1.3 CEQ（λ）学习算法

针对各类发电机组时滞环节所带来的控制延时问题［15］，本文引入了资格迹（Eligibility Trace）。资格迹通过详细记录各联合动作策略发生的频率对各策略的迭代Q值进行更新，可有效解决CEQ算法中的时间信度分配问题。由于通过相关均衡求取联合动作策略涉及到大规模的线性规划问题，求解过程繁琐且费时。因此，本文选取相对简单的TD（λ）［16］资格迹更新算法，如下：

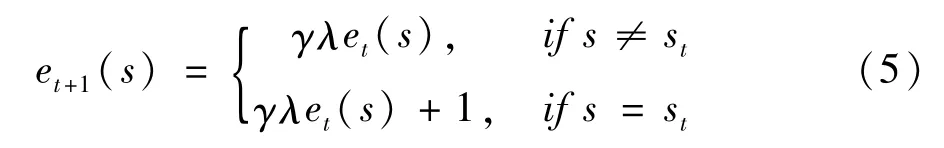
式中et（s）为时刻t状态s下的资格迹，st为时刻t实际的状态，γ为折扣因子，0≤γ≤1，λ为衰减因子，0≤λ≤1。

由式（2）～（4）可推导出 CEQ（λ）学习算法的迭代更新公式：

式中δj为单步值函数的迭代误差；γ为CEQ（λ）学习的奖励折扣因子；α∈（0，1）为学习因子，指明了对更新部分的信任度，α较大时算法收敛速度更快，而α较小时算法收敛更稳定。考虑到微电网发电的强随机性，结合仿真研究表明，α取值在0.001～0.1之间时，CEQ（λ）算法都具有良好的收敛特性。

2 微电网LFC模型

本文所研究的微电网包含光伏发电（PV）、风力发电（WT）、小水电（SH）、微型燃气轮机（MT）和飞轮储能（FW）五种微电源。其中，通过模拟文献［17］中全天光照强度的变化，建立了相应的光伏出力模型；对于风电模型，采用有限带宽白噪声模拟的随机风；小水电机组、微型燃气轮机和飞轮储能则分别采用文献［18-20］中典型模型。其中，光伏发电和风力发电日处理曲线分别如图1和图2所示。

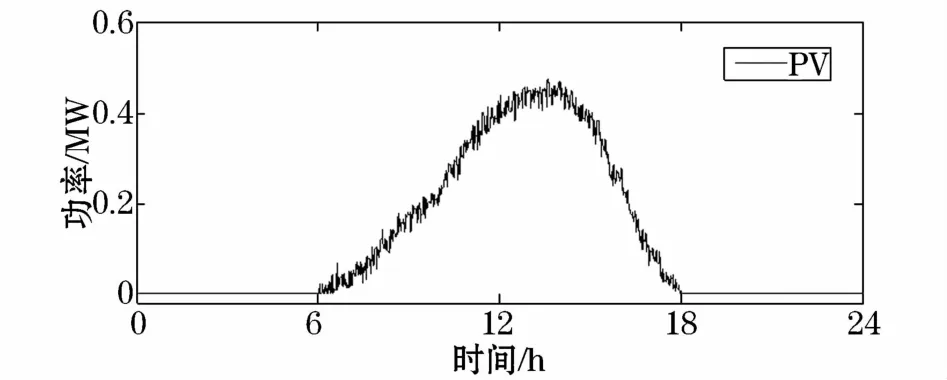
图1 光伏发电日出力曲线Fig.1 Daily output curve of photovoltaic generation

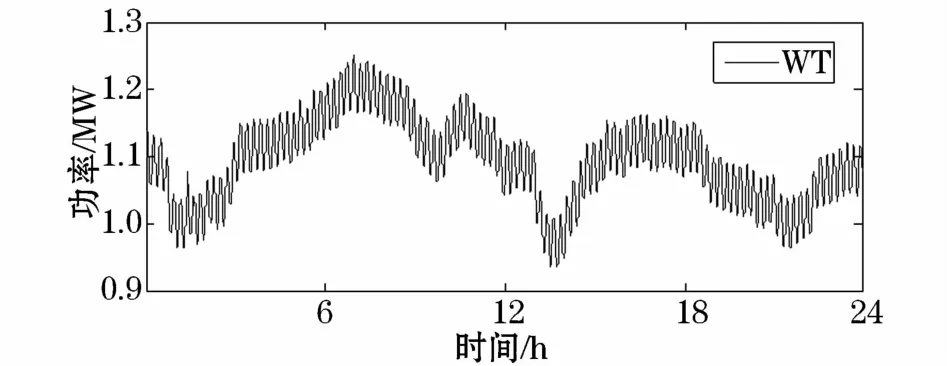
图2 风力发电日出力曲线Fig.2 Daily output curve of the wind power generation

由于本文采用的微电源均采用典型模型或常用模型，故对各微电源的性能不作赘述。其中，起调频作用的微电源SH、MT和FW的相关参数如表1。表中Ts表示机组二次调频时延；PGn为机组或储能的总容量分别分别表示机组或电源可调容量的上下限；Rup和Rdown则分别表示机组或电源的上调和下调速率。

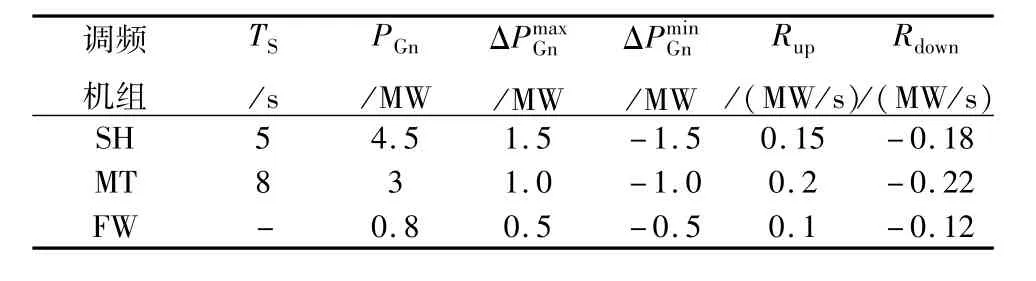
表1 调频机组参数Tab.1 Parameters of the micro-sources

由上述五种微电源组成的微电网LFC模型如图3所示。其中选取调节速度较快且较为经济的MT和SH为主调频机组，FW起辅助调频作用。光伏发电和风力发电由于具有较大的随机性和不可控性，可作为随机负荷处理。

微电网通过能量管理系统采集系统频率，将频率偏差作为智能频率控制器的输入，经过多智能体CEQ（λ）算法迭代计算和求解调度策略的相关均衡解，获得整体奖励值最高的最优调度指令，对主调频机组进行调节，从而实现保证微电网频率偏最小化的智能发电调度。

图3中所示的微电网频率响应模块包含微电网系统频率响应和飞轮储能频率响应，具体参数如表2所示［9］。其中，D表示微电网系统的阻尼系数（Damping Coefficient）；H表示微电网系统的惯性常数（Inertia Constant）；TFESS则表示飞轮出能力系统（Flywheel Energy Storage System，FESS）的时延；R1、R2、R3分别表示小水电、微型燃气轮机、飞轮储能一次调频的下垂常数（Droop Constant）。

表2 微电网LFC模型参数Tab.2 Parameters of the LFC model of MG

图3 微电网LFC模型Fig.3 LFC model of the micro-grid

3 基于多智能体CEQ（λ）学习的智能发电控制器设计

本文搭建的微电网LFC模型中包含2台主调频机组，即小水电和微型燃气轮机，需要2个智能体分别进行控制。每个智能体在所有智能体的动作概率分布基础上最大化自己的奖励值，达到整体奖励最大化的相关均衡，此时获得的联合动作策略为最优控制策略。

3.1 离散状态集和联合动作集的选取

考虑到微电网本身的系统特性，合理的离散状态集S和联合控制动作集A对多智能体CEQ（λ）学习的收敛特性意义重大。如果离散程度过高，联合控制动作集A的元素个数将呈幂增长，容易形成“维数灾”；相反，离散程度过低则会导致调频效果不佳，频率品质较低。

本文提出的智能发电控制器的状态输入为频率偏差Δf。IEEE 1547标准规定的分布式电源并网要求为Δf=±0.3 Hz（基准频率为60 Hz）；我国国家标准规定，正常运行工况下，电力系统频率应保持在50±0.2 Hz以内，对于容量较小的系统，频率偏差值可以放宽到±0.5 Hz。文献［21］标准要求风电场在49.5～50.2 Hz的频率偏离下能连续运行；文献［22］标准中规定光伏系统并网后允许频率偏差为±0.3 Hz；文献［23］标准要求分布式电源在49.5～50.2 Hz的频率范围内能连续运行。考虑到对含多种分布式电源的微电网频率范围尚未有统一的国家标准，本文结合上述各类标准，选择较为保守的50±0.2 Hz作为微电网运行频率范围，并设置的离散状态集为S={（-∞，-0.2），［-0.2，-0.15），［-0.15，-0.05），［-0.05，0.05］，（0.05，0.15］，（0.15，0.2］，（0.2，+∞）}。

CEQ（λ）学习的联合动作集A，亦即智能发电控制器的输出，为一组 AGC联合调度指令（ΔPSH，ΔPMT）。经分析调频机组的可调容量及其自身微电源发电特性，本文设置的联合动作为

其中，ASH和AMT分别为小水电和微型燃气轮机的输出动作集，且ASH=AMT=（-0.1，-0.05，-0.01，-0.001，0，0.001，0.01，0.05，0.1），单位兆瓦（MW）。

3.2 奖励函数的设定

本文通过各机组最优联合动作来实现微电网频率偏差最小化控制，对于智能体i的评价奖励函数Ri为：

式中μ1i、μ2i、μ3i和μ4i为各状态区间下奖励函数对应的权值，本文分别取1、2、4、8；Δf为系统频率偏差值；ΔPGi和ΔPorderi分别为机组i的实际调整出力和目标调整出力。因子|ΔPGi-ΔPorderi|+1可有效解决多智能体出力调节越限和智能体之间反调的问题。

3.3 均衡选择函数

在采用线性规划求取多智能体相关均衡的过程中，需要给定均衡选择函数。常用的均衡选择函数有如下四种［24］：功利主义（utilitarian），即最大化所有智能体奖励的总和；平等主义（egalitarian），即最大化所有智能体中奖励值最小者的奖励；富豪主义（plutocratic），即最大化所有智能体中奖励值最大者的奖励；独裁主义（dictatorial），即在状态s下，对于任意智能体i，最大化个体奖励值最大者的奖励。

其中，后三种均衡选择函数均侧重于最大化个别智能体的报酬值，而第一种功利主义均衡选择函数公平对待每个智能体的报酬值，最大化所有智能体报酬

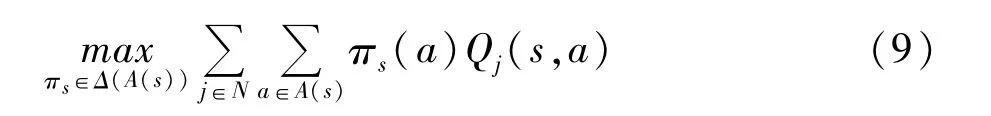
3.4 CEQ（λ）算法流程

微电网智能发电控制器的多智能体CEQ（λ）算法完整描述如下：值之和，这对关系到微电网全局稳定的有功-频率控制具有重要意义，故本文选取此种。功利主义选择函数表达如下：

4 仿真算例研究

本文微电网LFC模型采用Simulink仿真平台搭建，多智能体CEQ（λ）算法及智能发电控制器由S函数编写，模型如图1所示。其中调频机组总可调容量，其余参数详见表1和表2。

强化学习有在线和离线两种预学习模式。考虑到在线预学习过程中试错寻优可能会导致系统振荡而危害系统安全性，本文控制器采取先离线预学习，经过足够迭代次数收敛于最优联合动作策略π*后，再投入微电网系统参与在线优化运行。

根据文献［11］的研究，可知R（λ）学习算法较Q学习，Q（λ）学习算法控制效果好。故本文将 CEQ（λ）学习的控制性能与整定良好的PI控制和R（λ）控制作对比分析。算例包括典型扰动的预学习和中长期控制性能的仿真与分析。

4.1 典型扰动预学习

4.1.1 正弦扰动

在预学习阶段，给系统分别施加周期为1 000 s，幅值为2 MW的正弦负荷扰动。图4（a）和图4（b）分别给出了正弦扰动下R（λ）控制器和CEQ（λ）控制器的负荷跟踪曲线和频率偏差曲线。从图中可以看出，CEQ（λ）算法预学习在第一个正弦波周期内已基本收敛，收敛速度较R（λ）算法有很大的提高，而且能更为精确的跟踪负荷变化。

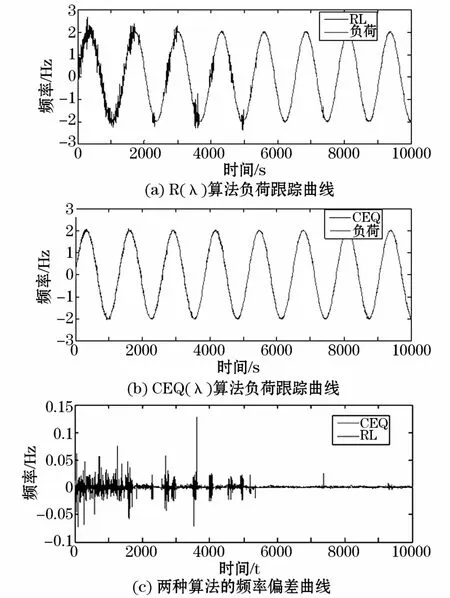
图4 正弦扰动下两种算法的预学习Fig.4 Pre-learning of two algorithms under sine disturbance

4.1.2 连续阶跃扰动

系统在受到连续阶跃负荷扰动下，各控制器的动态性能如图5所示。各次负荷突增的幅度分别为0.8 MW、0.5 MW、0.3 MW。

图5（a）和图5（b）给出了R（λ）学习算法和CEQ（λ）学习算法在连续阶跃扰动下的负荷跟踪曲线和频率偏差曲线。从图中可以看出，R（λ）学习算法并不能很好的跟踪负荷扰动，总输出曲线波动较大，而CEQ（λ）学习算法能更迅速，更准确的跟踪到阶跃负荷扰动，且输出波动较小，显示出良好的稳定性和准确性。

4.2 中长期控制性能分析

目前，国际上普遍采用一种基于平均值和统计性指标的CPS标准来考核大型互联电网AGC系统的中长期控制性能。对于孤岛运行的微电网而言，频率的长期统计性指标也可作为一种智能发电控制的考核标准。为了验证CEQ（λ）控制器在复杂负荷扰动和系统模型结构发生变化的情况下的在线学习能力和动态寻优能力，本文设置以下两组试验作比对分析。

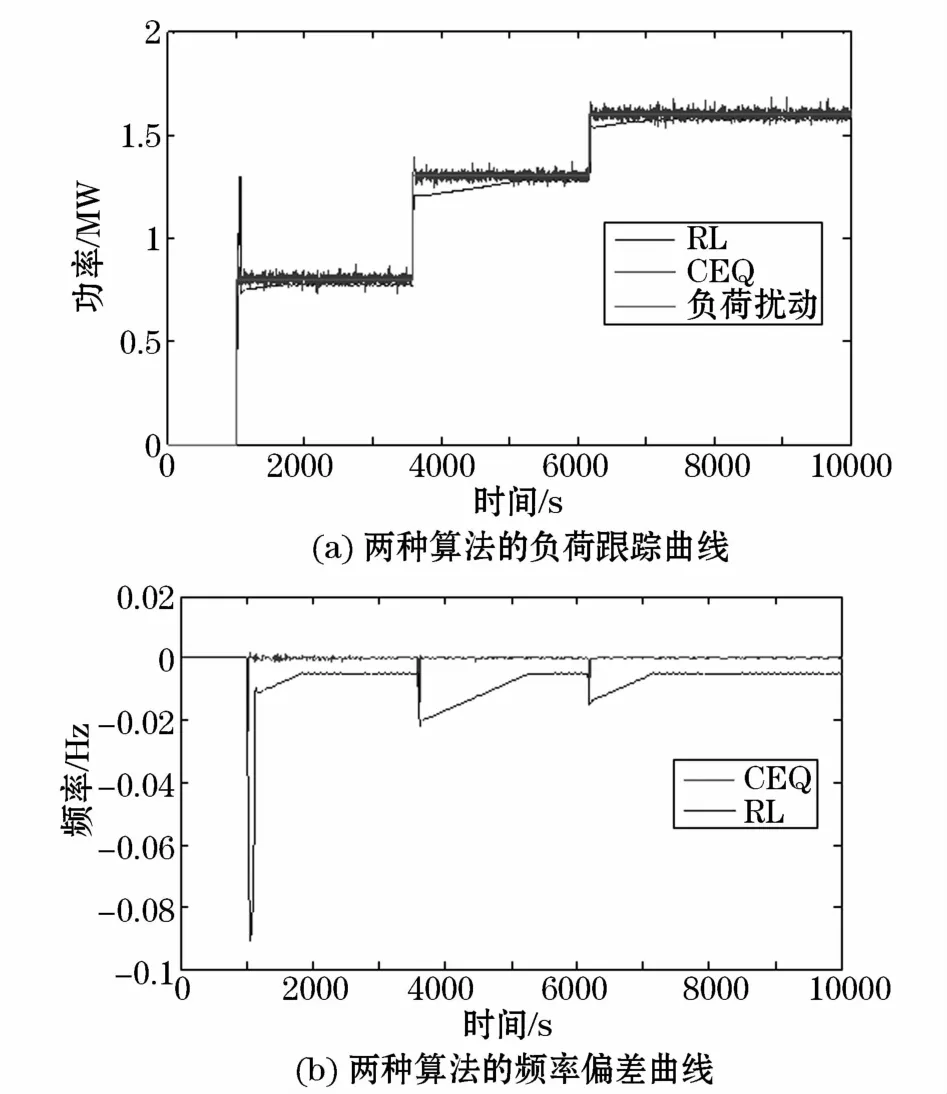
图5 连续阶跃扰动下两种算法的预学习Fig.5 Pre-learning of two algorithms under continuous step disturbance

考虑到大多数真实系统无法忍受在线学习前期CEQ（λ）控制器较差的跟踪性能，通常有两种处理方法。第一，先对CEQ（λ）控制器进行正弦波和连续阶跃扰动的预学习，然后再投入真实系统。正弦波变化较平缓，阶跃扰动变化急剧，经过这两种扰动类型的预学习，CEQ（λ）控制器基本可以直接适应真实系统中其他类型的扰动，故可以投入使用。第二，真实系统先采用传统控制器进行控制，而先将CEQ（λ）控制器并列投入真实系统直接进行预学习，这个阶段系统并不采用CEQ（λ）控制器的输出指令，待在线仿真中CEQ（λ）控制器的输出效果稳定后，再切换使用CEQ（λ）控制器。算例中，CEQ（λ）控制器在投入运行前，先经过上文中正弦波扰动和连续阶跃扰动的预学习训练，以提高CEQ（λ）控制器在微电网系统中的在线学习效率，减少在线学习过程带来的扰动。

4.2.1 随机性扰动下的频率指标考核

在标称参数下，给系统施加采样周期为10 min，最大幅值不超过2 MW的白噪声随机扰动。检测24 h内以系统频率偏差的绝对值|Δf|为考核对象的各项指标，如表3所示。从表中数据可以看出，与传统的PI控制相比，基于强化学习的智能控制器各项指标都更优。而CEQ（λ）控制下的|Δf|的最大值显著降低，合格率达到百分之百。可见CEQ（λ）在随机性强的复杂负荷扰动下仍有良好的控制效果。

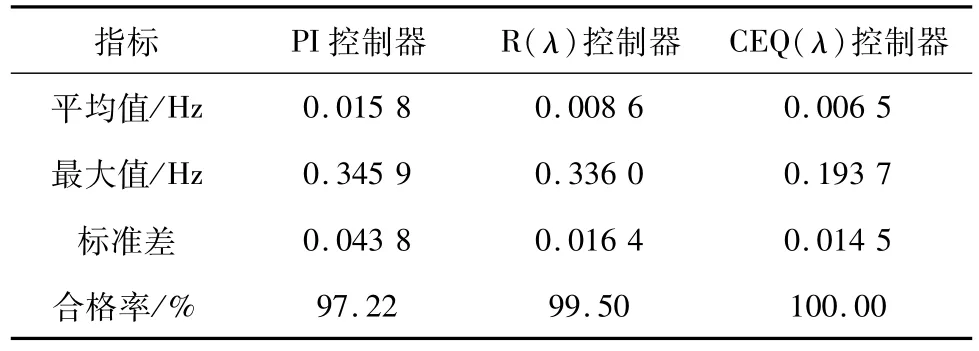
表3 随机性扰动下的频率指标考核Tab.3 Frequency index assessment under stochastic disturbance

4.2.2 系统参数变化时的频率指标考核

在上述随机扰动的基础上，对微电网自然频率响应系数施加10%以内的白噪声参数摄动；并在10 h时将风力发电退出运行。检测24 h内|Δf|相关指标的统计值如表4所示。经分析可知，具备在线学习和自适应特性的强化学习智能控制能更好的适应系统参数和结构变化的运行工况；基于多智能体相关均衡理论的CEQ（λ）比单智能体的R（λ）具备更强的在线学习能力和寻优能力。

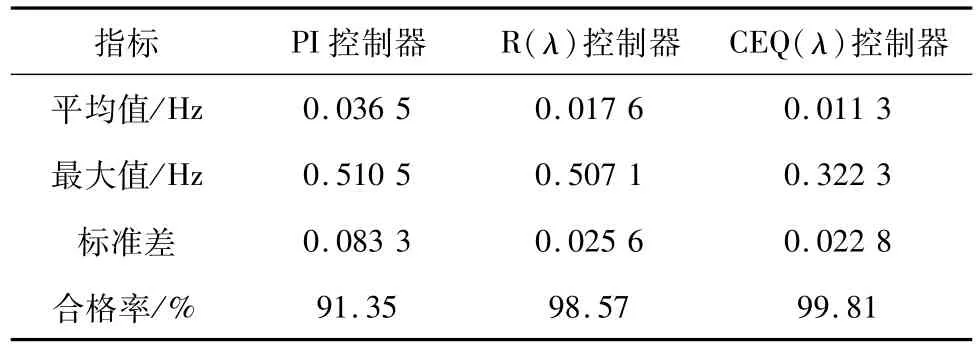
表4 系统参数变化时的频率指标考核Tab.4 Frequency index assessment under the changing of system parameters

5 结束语

本文提出了一种全新的多智能体CEQ（λ）智能控制器用于实现孤岛运行模式下的微电网频率控制和自动发电控制。该控制器具有以下特点：

（1）与传统PI控制器相比，多智能体CEQ（λ）控制器具备在线学习和自适应的特性，能更好的适应孤岛运行模式下微电网系统参数和结构变化等复杂工况；

（2）与单智能体R（λ）学习算法相比，多智能体CEQ（λ）学习算法联合动作空间更大，动作组合更丰富，因此能更精确的跟踪负荷变化；多个智能体协同学习，能更有效、更快速的寻找到相关均衡平衡点，从而提高算法收敛速度；

（3）由于多智能体CEQ（λ）学习算法涉及到多个智能体之间的协同学习，当调频机组较多时，联合动作空间骤增可能导致“维数灾难”问题，可考虑采用聚类分层的方法来进一步解决。