一种基于图论剪枝算法的多分支配电网行波故障定位算法*
贾惠彬,李明舒,张国云
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引 言
行波故障测距法在当前的输电线路故障测距中得到了广泛的应用[1-2]。传统的行波测距法可分为单端法和双端法。其中,双端法只利用输电线路两端的波头信息,不需要考虑行波的折射、反射问题,故障定位结果较为可靠。随着GPS同步时钟和数字信号处理器技术的发展,双端行波定位方法的优势越来越凸显。
而配电网在结构上较为复杂,多为树形辐射状结构,且分支较多。因此很难直接采用双端法定位。就此问题很多专家学者做了相关研究,文献[3]利用了配电网故障后的初始电压、电流信号来实现双端定位。由于故障回路电抗与故障距离成正比,可据此求出测量点到故障点的线路距离[4-5]。文献[6]提出了利用多端电压行波对电力线路进行故障定位的方法,通过检测行波信号的前两个波头来确定故障发生时刻。文献[7-9]通过在线检测故障暂态电流和电压行波来进行双端法故障测距。文献[10-11]分别从网络和图论两方面对适用于输电线路的双端法进行了研究分析。对于将行波定位理论应用于配电网,尤其是低压配电网,目前的研究还不够完善。
通过对图论以及简直算法的研究,本文提出了一种适用于配电网的行波故障定位新方法。该方法利用配电网末端检测到的暂态行波信息进行故障定位。其特点是将配电网结构等效成图论拓扑结构,并构建基于图论的权值矩阵以及最小生成树。采用剪枝算法,剔除无效的波头信息,最终实现配电网故障的实时精确定位[12]。
1 基于图论的配电网拓扑结构建模
配电网的结构多为树形辐射状,从图论的角度上看,由于可以不考虑内部元件特性,只考虑行波传输网络。因此,配电网络可以抽象成由顶点和边组成的集合,如图1所示。其中,结点A、B、C、D表示配电网电源和末端变压器;a、b、c、d表示线路的交叉节点;此外,用无向图的边表示配电网线路,线路长度作为边的权值。
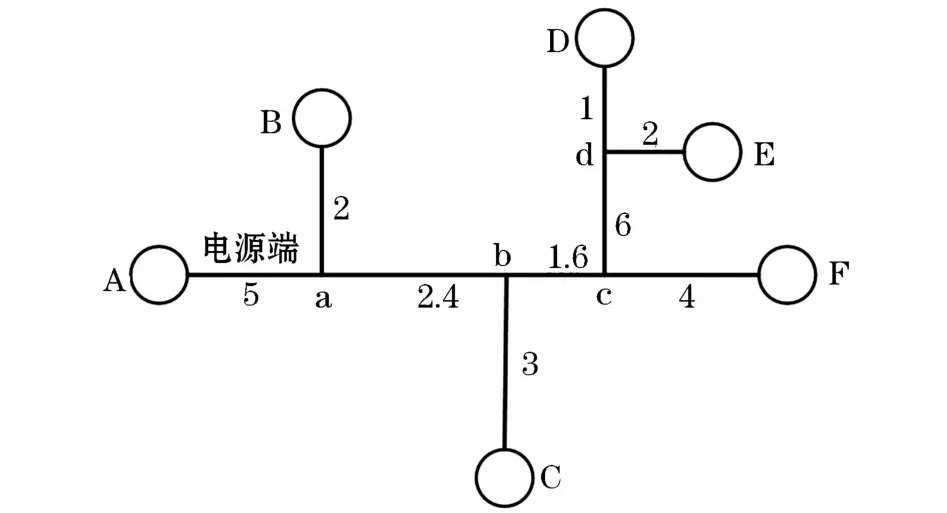
图1 配电网简化拓扑图Fig.1 Simplified topology diagram of distribution network
由配电网简化拓扑结构图,可利用求最短距离dijkstra算法,可以求得各个节点间的距离矩阵G和关联矩阵
式(1)中,距离矩阵G里的每个数字为节点间最短距离;式(2)和式(3)中数字表示两个节点之间最少经过的边数,也就是关联情况。由式(1)~式(3)可以表示图1中配电网中各点之间的关系,且为建立最小生成树提供依据。

由于发生故障后的暂态行波信号在输电线路传中是沿着最短路径传播的,因此选择权值总和最小的生成树—最小生成树(MST)便可以描述行波的传播路径。由于配电网的结构特点可知,其最小生成树是二叉树。因此,可以利用最小生成二叉树及剪枝算法来进行故障定位判定[11-15]。
首先,将距离矩阵(1)和关联矩阵(2)~矩阵(3)输入到计算机中,根据prim算法求出最小生成树的矩阵形式。然后画出如图2所示的最小生成树结构图。根据图论方法中最小生成二叉树的存储方式,计算机可以对它进行有序的查询,并将由各个端点采集到的行波信息,存储在最小生成二叉树的结构中。其中,交叉节点作为最小生成树中的各个根结点,各个终端作为叶子节点。
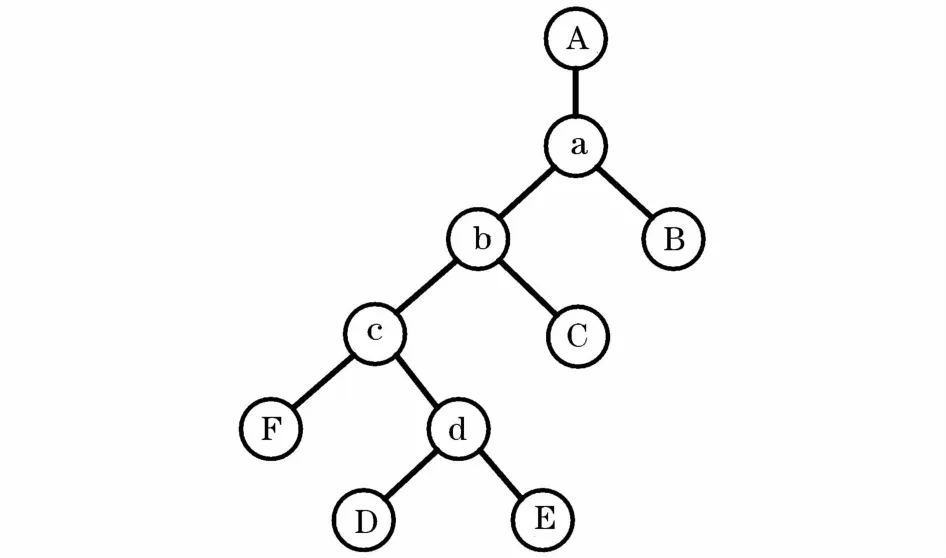
图2 最小生成二叉树Fig.2 Minimum spanning two fork tree
配电网由于其多分支结构而无法直接利用输电线路行波故障测距方法。以上通过借鉴最小生成树对配电网模型进行分析,可以有效解决该问题。
2 基于EBP后剪枝算法的配电网故障定位方法
配电网可在其各个终端配置终端变压器用来检测故障初始行波信号,由于配电网多分支的结构特点,配电网故障定位有两个难点:(1)真伪故障点的判断;(2)如何利用剪枝算法进行故障分支的判断。
2.1 真伪故障点判断
如图3(a)中线路所示,当线路发生故障后,产生的行波信号以最短距离在线路中传播。终端变压器会检测首个行波波头信息,并记录其到达时刻。

图3 伪故障点Fig.3 Pseudo fault points
设图中A、B两端检测到的行波到达时刻分别为tA、tB。当故障点K在A、B最短路径以外时,由双端法距离计算公式计算出的故障点位置是b点,与真实的故障点位置不符,这里我们称之为“伪故障点”。双端法距离计算公式如下:

式中XAF为故障点到端点A的距离,lAB为线路AB的总长度。
若故障发生在 A、B之间,如图3(b)所示,则可以公式(4)直接找到故障点。
因此,配电网的难点在于如何排除伪故障点,从而精确的找到故障点。为了防止测量误差、传播损耗和行波衰减的影响,可将计算得到的故障距离与距离矩阵G中此节点到其他节点的距离Dij进行对比,并依据实际经验设定一个阈值δ,若满足公式:

则认为计算出来的故障点为伪故障点。此时故障点发生在b节点或AB以外的分支上,需要利用最小生成二叉树和剪枝算法进一步分析。
2.2 EBP剪枝算法
剪枝算法是一种程序优化算法,广泛应用于博弈学以及数据挖掘的决策树中,也是搜索算法中最关键的一环。剪枝就是采用某种规则将搜索树中的部分“枝条”修剪掉。本文所用的EBP后剪枝算法的原理和步骤如下[16]:
EBP后剪枝算法通过对节点的错误概率估计进行剪枝操作。由概率论的知识分析可知,n(t)次事件中e(t)次发生的概率称为错分样本率r(t),其中[LCF、UCF]表示错分样本率的置信区间,CF是置信区间的置信水平,由公式(6)可求得置信区间的上限

置信水平CF的值决定剪枝的多少,CF取值越大剪枝越少,反之,CF取值越小剪枝越多。C4.5中CF=0.25,其中错分样本的概率服从二项分布。EBP算法自底向上进行剪枝操作[18],分为如下三步:
第一步:计算置信区间上限UCF,假设错分样本概率服从二项分布,令E=e(t),N=n(t),可以得出:
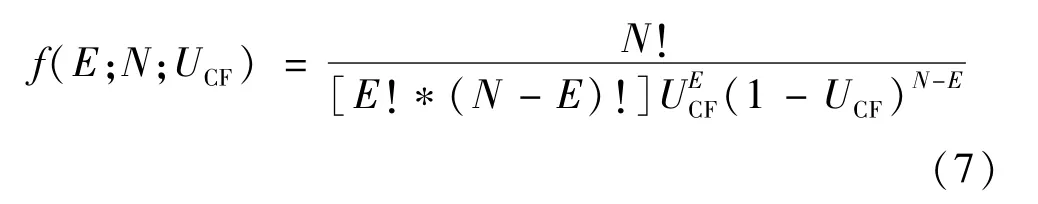
式中f表示N次实验发生E次错误的概率,UCF为一次错误发生的概率,由公式(7)可知:
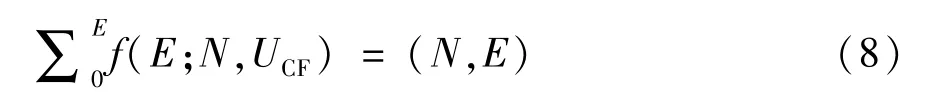
第二步:计算叶节点的预测错分样本的个数。叶节点的预测错分样本数等于到达该叶节点的样本数与该叶节点的预测错分样本率UCF的乘积[17]。
第三步:判断是否进行剪枝以及具体剪枝方法。
分别计算如下三种预测错分样本数:
(1)计算以节点t为根的子树T的所有叶节点预测错分样本数之和E1;
(2)计算子树T被剪枝以叶节点代替时的预测错分样本数E2;
(3)计算子树T的最大分支的预测错分样本数E3。
最后对三个值进行比较:E1最小时则不剪枝;E2最小时则进行剪枝,把子树剪掉并代以一个叶节点;E3最小时采用“嫁接”策略,即用这个最大分支来替代子树[17]。
EBP中CF值控制剪枝的强度:当CF=1便不需要剪枝;设定较高的CF值表明此时错误可以被接受;较低的CF表明错误较多需要进行大量的剪枝。基于同样的搜索树来说,较小的CF的叶子节点的错误率要高于较高的CF值的错误率[17]。
2.3 算法流程
按照上述EBP后剪枝算法,对于已经建立好的最小生成树,需要采用剪枝算法来进行定位故障。其算法流程如下:
首先由公式(4)计算出的故障距离Xij,进而采用EBP剪枝算法:
“那个治库工程咱能帮着吆喝?”“治库工程咱得甩手,那破事,钱再多也不能帮他瞎吹。我了解了下,魏昌龙这人在当地口碑不错,你再下去捣鼓篇人物专访。你文字功底好,转行搞新闻上手快,不错。陵矿这个版是你拉来的,按规定你提成10%。”
第一步:求置信区间上限UCF。由公式(6)、公式(7)计算置信区间上限UCF,其中:
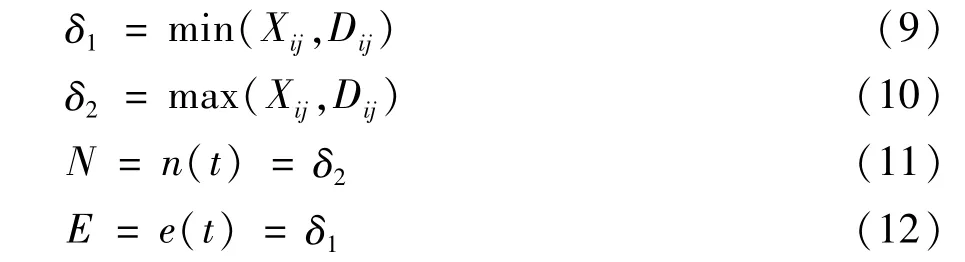
这里置信区间的上限UCF越高则不容易进行剪枝;较低的UCF说明隐含有更多的错误,则容易被剪枝。而对于同样节点来说,采用较小的UCF值叶节点上要比UCF值较大情况下的剪枝的概率大[19];
第二步:判断是否进行剪枝。对于节点t的叶节点时间信息t1、t2,由公式(4)计算出X12,然后由式(9)和式(10)计算δ,其中:

若δ在置信区间[LCF、UCF]内,则说明故障点是伪故障点,则进行剪枝操作;
第三步:进行剪枝操作。将各个节点的能量序列E类比于预测错分样本数,选取最小生成树的最底层对每一层进行分析。首先以节点t为根的子树t1节点的能量为E1,t2节点的能量为E2,将两值进行比较,如果E2>E1,则进行剪枝操作,把t1子树剪掉并采用“嫁接”策略以t2叶节点来替代子树。同理如果E1>E2,则用t1叶节点来替代子树。这样往上推进一层,加入新的叶子节点,进行判断,直到找到真正的故障点为止。
上述步骤的算法流程图如图4所示。其定位过程为:首先选取最末端的叶子节点如F、G两点的时间信息tF、tG,由公式(4)计算得出故障距离x。将其与距离矩阵中的DDf做比较,若不满足公式(5),则计算的定位故障点为真实故障点,可以输出显示定位结果;若满足公式(5),则表明计算出的故障点为伪故障点,需要采用剪枝算法处理,根据上述的信号瞬时能量序列得到检测点的能量大小排序序列,对两个分支的预测错分样本数EF和EG进行比较,按照“嫁接”策略,较大者叶子节点来作为子树替代f点的位置。再将保留的叶子节点与上一层的节点E按照EBP剪枝算法进行故障定位直到找到故障点。
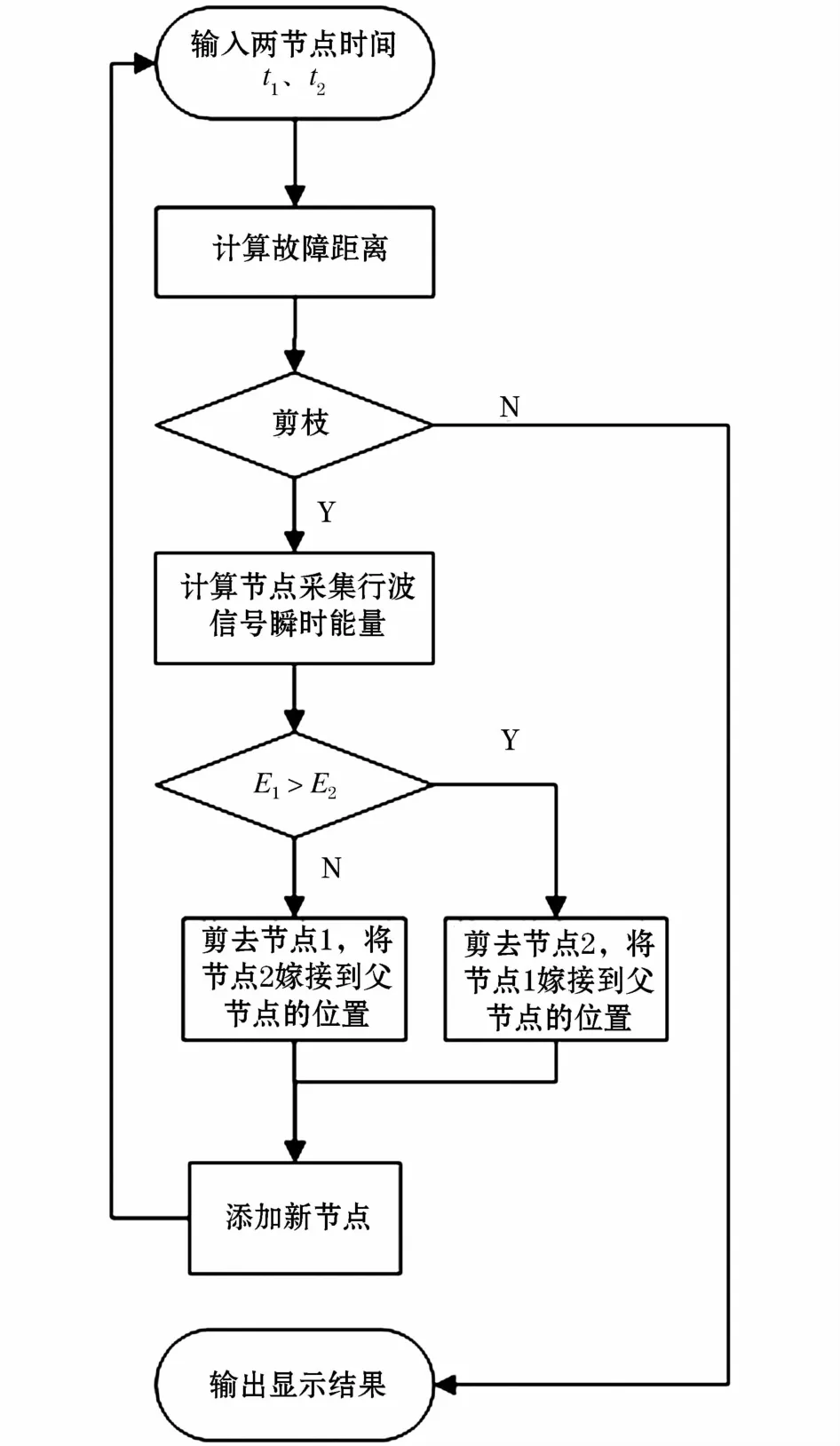
图4 剪枝算法流程图Fig.4 Flow chart of pruning algorithm
3 仿真分析
3.1 仿真模型
本文利用电磁暂态PSCAD/EMTDC仿真工具建立10 kV单电源供电的配电网模型,其拓扑结构如图5所示。线路采用分布式参数模型,电源为220 kV输电网末端,变压器采用1 000Ω的接地电阻。模型中的380 V线路采用中性点直接接地。为了保证双端法的时间同步,要求线路末端测量系统要有精确到微秒的同步时钟,以实现末端的时间同步问题,在此定位系统中可以采用北斗时钟同步系统进行定位。在每个变压器的一次侧安装电压测点,用来检测故障瞬间电压的变化情况。综合考虑其他条件,仿真中采样频率1 MHz,为了减少波速的影响,波速采用在线测量:v≈2.993 540 3×108m/s。
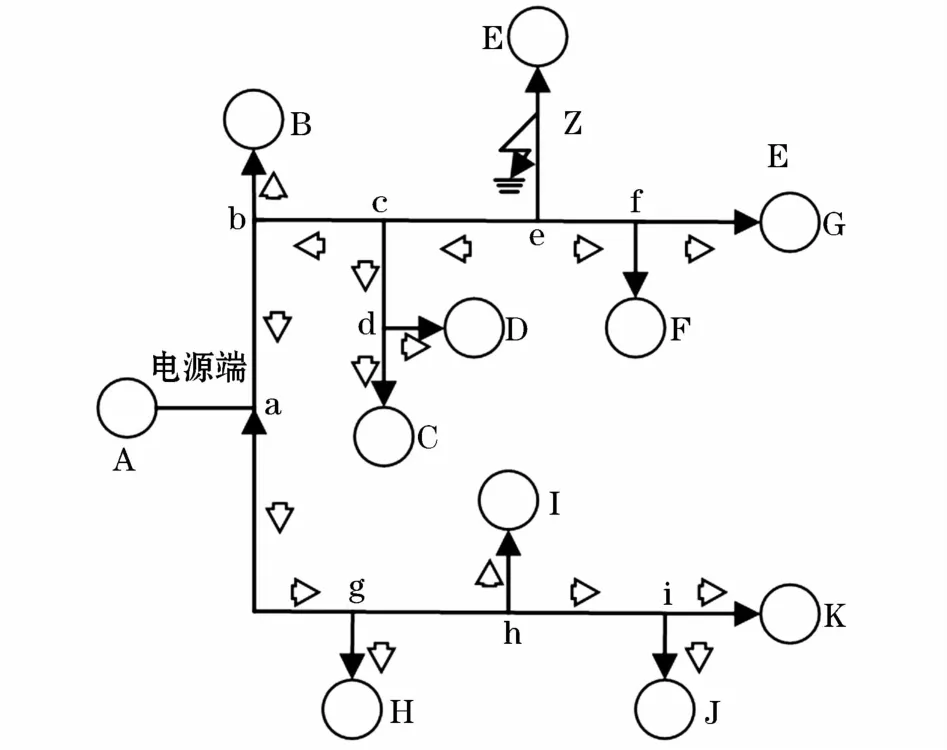
图5 配电网仿真拓扑建模Fig.5 Topology model in simulation of distribution network
将此拓扑模型的距离矩阵G和关联矩阵H1和H2输入到计算机中,根据prim算法求得的最小生成树如图6所示。
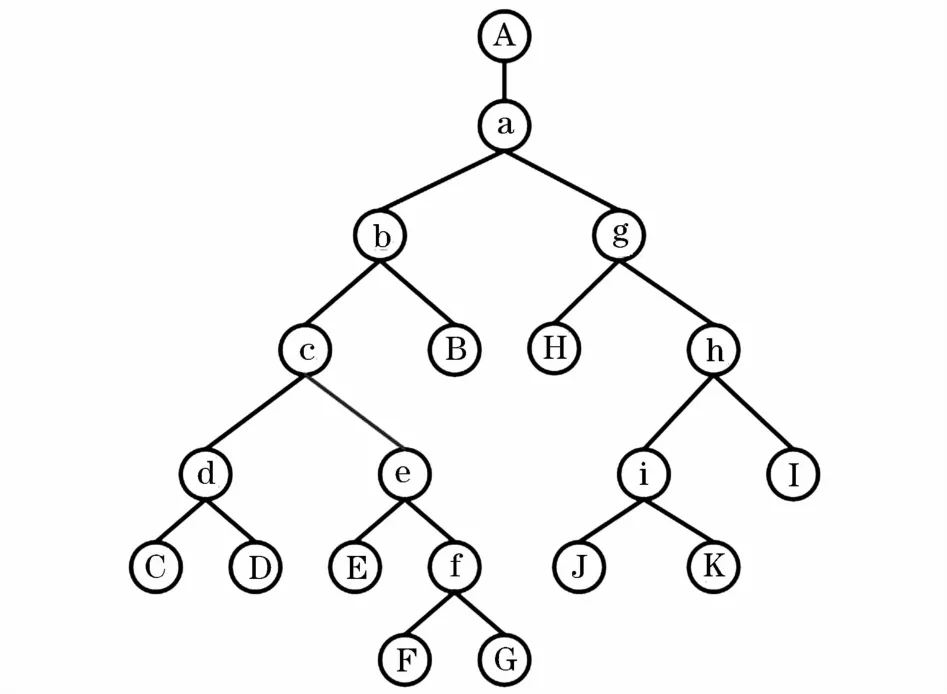
图6 定位最小生成二叉树Fig.6 The location of minimum spanning two fork tree
3.2 波头提取
传播过程中,行波遇到波阻抗不连续点时发生折射、反射,因此距离故障点越远、经过波阻抗不连续点越多,终端检测点检测到行波到达时衰减越严重,检测到的故障行波信号高频分量越少。故可以利用这个原理根据信号的衰减情况,对检测信号终端设备进行排序,形成行波检测点编号序列E。另外,本文采用Teager能量算子(TEO)计算信号的瞬时能量并检测信号的衰减情况。由此可根据计算行波信号能量的大小来对检测点进行排序,形成监测点编号序列E。
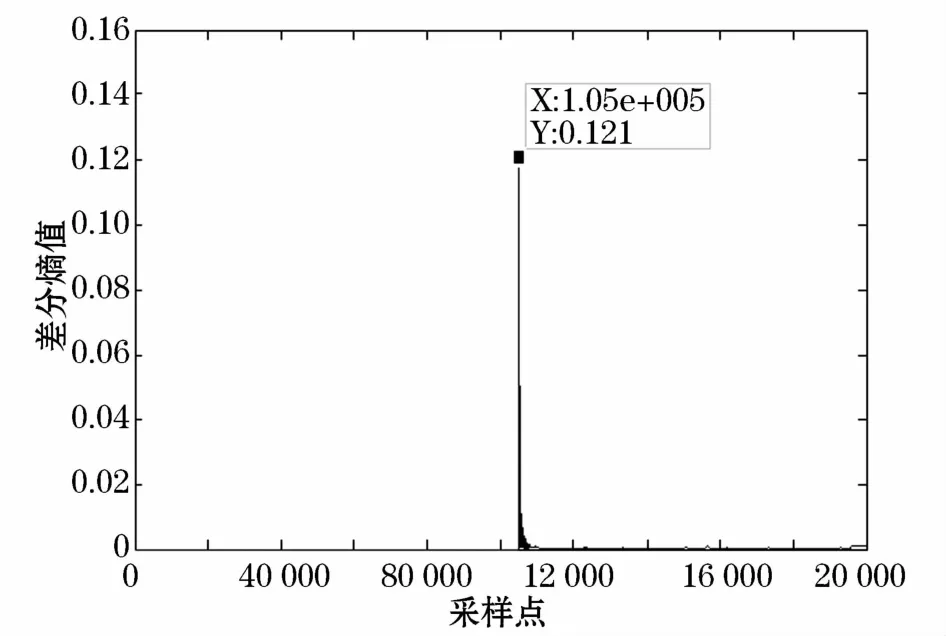
图7 行波波头的检测结果Fig.7 Detection result of wave front
3.3 仿真结果
首先检验该方法对于不同故障类型的适用性,在配电网模型中设置单相接地故障,故障点设置在Ee之间,距E点3 km。各个终端设备分别对行波波头到达的时间信息和能量信息进行检测。分别利用LMD-DE和Teager能量算子检测首个电压行波到达时刻和能量信息进而建立终端检测序列:R=[EE、EF、EG、ED、EC、EB、EA、EH、EI、EJ、EK],达时刻越早,能量越大。最小生成树的叶子节点代表各个检测终端检测到的时间和能量信息,按照基于EBP后剪枝算法的配电网故障定位方法对此模型进行故障定位,剪去的枝叶G。计算出故障距离x=,与实际故障距离误差为97 m。
在Bb之间距B端2.4 km处设置AB两相短路接地故障。利用同样方法采集各个终端的行波波头到达的时间信息和能量信息,并根据检测到的时间和能量信息建立终端序列组,R=[EB、EA、ED、EH、EF、EC、EI、EE、EG、EJ、EK],按照基于 EBP后剪枝算法的配电网故障定位方法对此模型进行故障定位,依次剪去的枝叶是G、E、C、F。计算出故障距离x=误差为64 m。
故障初始角度是影响行波波头的检测的重要因素之一,本文仿真故障初始角分别设为90°、60°、45°和30°四种情况[20],故障类型为单相接地故障,设置在距图5中K检测点4 km处,仿真结果如表1所示。
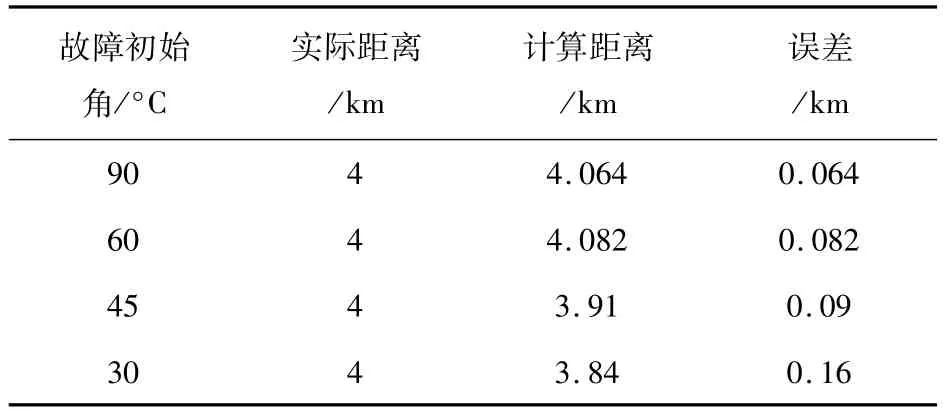
表1 不同故障初始角故障定位结果(A-G)Tab.1 Location results in the condition of various fault inception angle(A-G)
故障接地电阻大小对故障定位精度有重要的影响。为了验证该方法的适用性,实验中接地电阻R分别设置为20Ω、50Ω、100Ω和300Ω四种情况。表2列出了在故障初始角为90°时,距测试A点5 km处发生单相接地故障时的仿真结果。
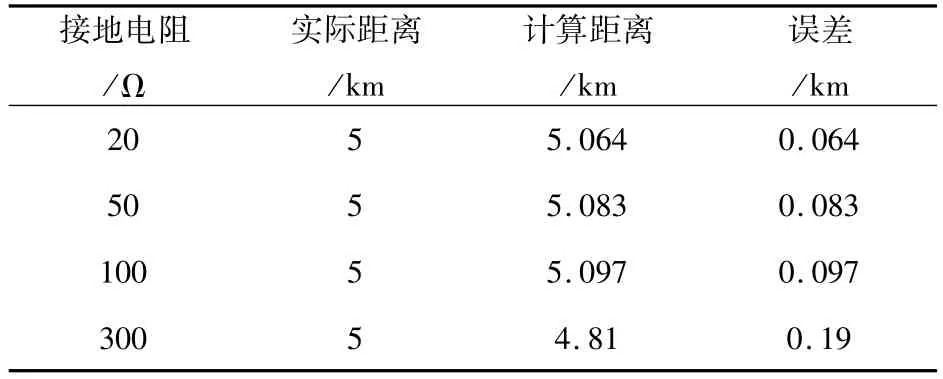
表2 不同接地电阻故障的定位结果(A-G)Tab.2 Location results in the condition of various fault resistance(A-G)
由以上实验结果可以看出,基于决策树剪枝算法的配电网行波故障定位方法能够快速、准确的找到配电网接地故障点,且对于多种不同的故障条件均有较好的适用性。
4 结束语
基于图论剪枝算法提出了一种多分支配电网行波故障定位的新方法。理论分析和仿真结果表明,根据该方法所获得的定位结果较为精确且适用于多种故障条件。该方法对于实现将传统的输电线路行波定位法应用于配电网中具有重要意义。

