基于群智能强化学习的电网最优碳-能复合流算法*
郭乐欣,张孝顺,谭敏,余涛
(1.华南理工大学 电力学院,广州 510640;2.广东省绿色能源技术重点实验室,广州 510640)
0 引 言
随着温室效应给环境带来的影响日益严重,低碳经济逐渐成为各能耗工业的重点发展方向。其中,电力工业作为最大的CO2排放企业,将在低碳经济发展中担任重要的角色[1]。现有很多关于低碳电力的研究,包括最优潮流、经济调度、机组组合、碳储存和碳捕捉等问题[2-5],主要是对发电侧的碳排放进行优化。文献[6]从用户角度,提出碳流追踪模型来计算用户的碳排放强度,分摊用户侧碳排放责任。相比于电力行业传统的碳排放计量方式,从用户侧计量碳排放是一种考虑电量传输过程,尊重需求产生供给原则的计量方式。为了与发电机侧碳排放量的概念进行区分,本文定义转移到用户侧的碳排放量为碳排放损耗。在厂网分离情况下,电网企业承担与其有功网损相对应的碳排放损耗责任。
通过建立电网碳排放流的计算模型[7],笔者提出了一种多步回溯Q(λ)学习算法,解决了电网侧的最优碳流问题[8]。然而,文献[8]所用的最优碳流模型并不能清晰地解释电力网络中能量流和碳排放流的分布情况。因此,在本文中笔者进一步建立了一种电网的最优碳-能复合流(Optimal Carbon-energy Combined-flow,OCECF)的通用新模型:即在满足系统运行和安全约束的前提下,通过对电网的无功进行优化,使得电力网络中的能量流和碳排放损耗达到最小。
另外在后续研究中我们发现,与其它经典优化算法和人工智能优化算法相比较,虽然Q(λ)算法收敛鲁棒性更强,但是算法只依靠单个主体进行寻优,收敛时间较长,难以满足复杂电网碳流在线滚动优化的实时要求[9]。群智能(Swarm Intelligence,SI)是人工智能的一个分支学科[10],受社会昆虫、动物集体行为的启发,已经衍生出蚁群、粒子群、蜂群等智能算法,在电力系统领域得到了很好的应用。在群智能算法中,每个群体都会有多个主体,各个主体之间会进行信息交流或任务分工,从而实现协同优化,有效缩短了寻优时间。很自然地,有学者会联想到把强化学习与粒子群、蚁群算法进行结合,也陆续出现了一般改进性的群智能算法[11-13],但这些方法都仅仅停留在把群体优化与强化学习在算法流程上进行简单串行结合,两类不同性质的算法优势并未实现真正融合发挥,国际人工智能学术界一般也不认同这些方法为真正的群智能强化学习算法。
本文通过深入研究强化学习与群智能的数学原理,对传统Q(λ)学习和PSO多主体算法进行了深度地有机结合,提出了一种全新的群智能强化学习算法—PSO-Q(λ)算法,实现两类方法的优缺点的有机互补。PSO-Q(λ)算法对Q(λ)算法的最大改进之处在于:群体中的个体共享信息,各个粒子在每次迭代更新自身的Q值矩阵后,根据动作概率矩阵随机选择当前状态下的动作,然后利用自身历史最优动作和群体历史最优动作信息,对当前动作进行修正。
本文的框架主要包括:首先建立最优碳-能复合流的数学模型,然后描述了PSO-Q(λ)算法原理,并给出了算法解决OCECF问题的具体步骤,最后利用IEEE118节点算例仿真研究验证了PSO-Q(λ)算法的高效性和可行性。
1 最优碳-能复合流数学模型
1.1 碳-能复合流计算模型
电网的碳-能复合流是将电网的潮流和依附于电网潮流而存在的碳排放流结合,形成的综合网络流。其中,能流是实际网络流,碳排放流是虚拟网络流,在电力系统中可简称为碳流。碳流产生于发电环节,表征碳排放从电源侧向用户侧转嫁的概念,在数值上等于能流与对应电源侧碳排放率的乘积[14]。碳流与能流一样是由送电端向受电端流动,但是不同于能流,只有送电端会产生碳排放的电源才能称为碳源,如图1所示。
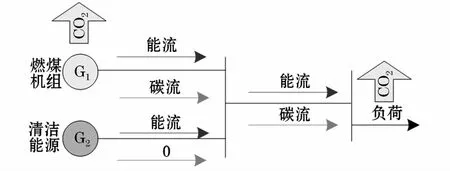
图1 电力系统碳-能复合流示意图Fig.1 CECF schematic diagram in power system
能流是电能在电网中的传输,在传输的过程中会出现功率损耗,通常称为网络损耗,一般描述如式(1)所示。

式中Vi和Vj分别是互联节点i和j的电压幅值;θij是节点i和j之间的相角差;gij是节点i和j之间的电导;NL是电网节点集合。
电网在传输电能的过程中,需承担网络损耗所对应的碳流损耗。电网碳排放流的追踪,以潮流追踪为基础,按照比例共享原则[15]来追溯网损来源。第w台发电机在节电j处占注入总有功的成分比例如式(2)所示。

式中Psw是发电机w的有功出力是等效无损网络中的j节点总有功注入是发电机w在节点j处的有功注入权重,具体推导过程参见文献[6]。
第w台发电机在节电j处出线的成分比例与之相同,线路损耗按照碳源对线路的利用份额分解,所以βsw,nj即为发电机w在支路i-j有功损耗的成分比例,电网支路i-j的有功损耗ΔPij如式(3)所示。

式中W是所有发电机集合。
由此,电网的总碳流损耗如式(4)所示。
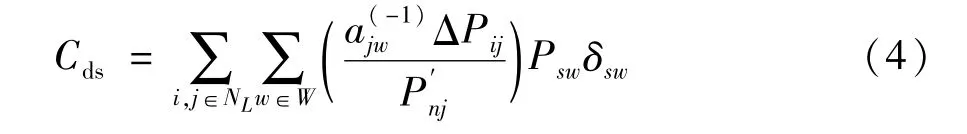
式中δsw是发电机组w的碳排放率。
1.2 最优碳-能复合流目标函数
本文的最优碳-能复合流算法是在满足电网各约束条件并充分考虑电网电压稳定的基础上,尽可能降低电网的网损和碳流损耗。所以本文综合考虑电网运行经济性和电网安全稳定性的多目标最优碳-能复合流模型目标函数如式(5)所示。

式中f1(x)为非线性函数描述的碳流损耗分量;f2(x)为非线性函数描述的有功网损分量;Vd为电压稳定分量;μ1、μ2为权重系数,μ1∈[0,1],μ2∈[0,1],μ1+μ2≤1;x=[V,θ,kt,Qc]T分别对应电网各节点电压值、各节点相角、有载调压变压器变比、无功补偿容量。其中,电压稳定分量[16]如式(6)所示。
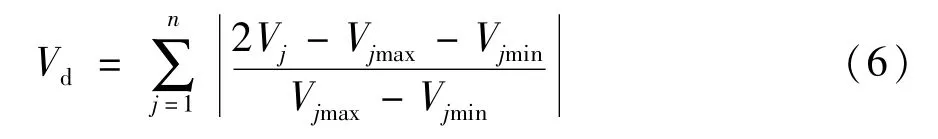
式中n是负荷节点个数;Vj是负荷节点j的节点电压;Vjmax、Vjmin分别是负荷节点j的最大、最小电压限制。
此外,该模型同样需满足电力系统潮流的等式约束和不等式约束,不再赘述,详见文献[16]。
2 PSO-Q(λ)算法原理
2.1 粒子群算法
粒子群算法启发于鸟群觅食[17],群体中每个粒子主要通过两个极值来交互协同优化,分别为个体极值Pi和群体极值Pg。在获知当前的两个极值后,个体i即可更新自身的速度和位置,如式(7)、式(8)所示。

式中Vi为第i个粒子的速度;Xi为第i个粒子的位置;ω为惯性权重;k是当前迭代次数;c1、c2(c1≥0,c2≥0)分别为学习因子;r1、r2是分布在[0,1]之间的随机数。
2.2 多步回溯Q(λ)学习
多步回溯Q(λ)学习(Multi-stepQ(λ)learning)是基于离散马尔可夫决策过程的经典Q学习结合了TD(λ)算法[18]多步回报的思想的强化学习算法。资格迹的引入能够解决延时强化学习的时间信度分配问题,获取算法行为的频度和渐新度两种启发信息,从而考虑了未来控制决策的影响[19]。其中,资格迹的更新规则如式(9)所示。
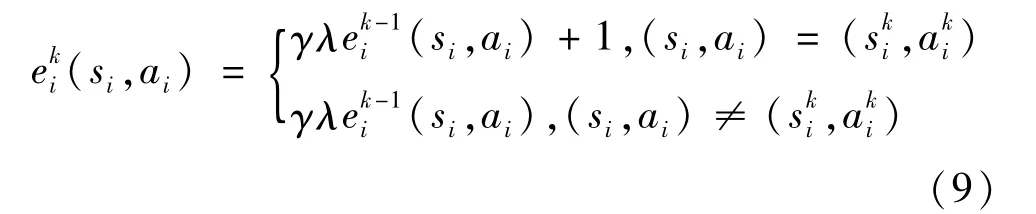
在引入资格迹后,Q(λ)学习迭代更新公式如式(10)、式(11)所示。
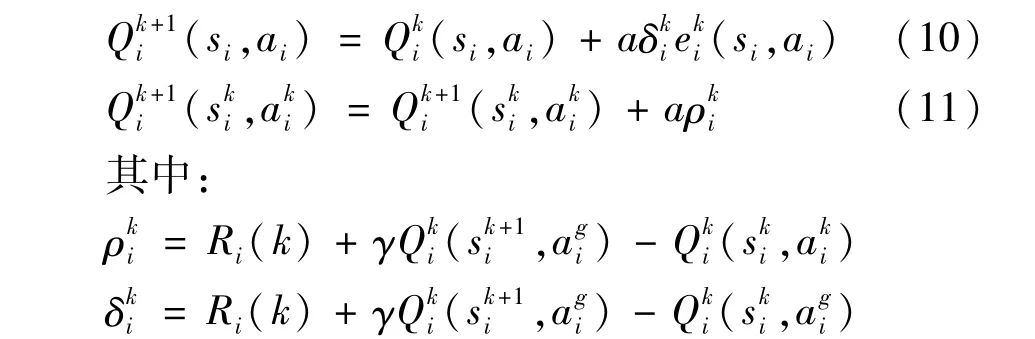

式中A为动作集合。
2.3 PSO-Q(λ)算法
对于所有个体来说,在更新完自身的Q值矩阵后,即可更新各自的动作概率矩阵,如式(13)所示。

式中Pi(si,ai)为个体i在状态si下执行动作ai的概率值;β(0≤β≤1)为动作搜索速度,β越小,算法越慢收敛,收敛效果越好。
根据更新后的动作概率矩阵,个体i即可随机选择当前状态下的预判动作预判动作类似于粒子群的个体位置,需要对其进行修正。其中,对于个体i来说,其个体最优动作即贪婪动作群体最优动作可求解如式(14)所示。

式中N为群体集合。
因此,根据式(7)和式(8),本文取ω=0,则 PSOQ(λ)修正后的动作更新如式(15)、式(16)所示。

3 基于PSO-Q(λ)的最优碳-能复合流算法
3.1 算法状态与动作的设计
在碳-能复合流计算时,首先有必要对日负荷曲线进行离散化,确定不同时刻的负荷值,然后求解出不同时段的最优解。本文按照负荷消耗的能量的差别,把负荷离散化划分成不同的断面,每一个断面即对应一个状态s。
在碳-能复合流优化计算中,可控变量包括:有载调压变压器变比、无功补偿容量等。本文算法的动作空间与可控变量一一对应。
3.2 奖励函数的设计
PSO-Q(λ)学习中,对于所有个体而言,立即奖励函数都是体现系统优化的方向。为了实现电网的碳-能复合流优化,根据式(5)给出的目标函数,本文的奖励函数可设计如式(17)所示。

式中C是常数,用于保证奖励函数值为正数;Cds为碳流损耗;Ploss为网损;μ1、μ2分别为目标系数,μ1较大时,则表明电网企业更加偏好于碳流损耗,μ2较大时,则表明电网企业更加偏好于网损;N是不满足不等式约束的个数,引入这个参数是为了保证最终选定的最优动作能够满足电网潮流计算的不等式约束。
3.3 算法流程
本文提出的基于PSO-Q(λ)的OCECF算法具体流程包括:个体自身的更新迭代和多主体的协同输入,具体步骤如图2所示。

图2 基于PSO-Q(λ)的最优碳-能复合流算法流程图Fig.2 Flow chart of OCECF based on PSO-Q(λ)
4 仿真算例研究
本文算例是在Matlab7.10仿真平台上借助Matpower4.1软件包中的潮流计算程序,并在CPU为3.1 GHz内存为4 GB的计算机上对IEEE118节点标准算例进行的仿真。为验证PSO-Q(λ)算法的性能,算例中引入遗传算法 (GA)[20]、量子遗传算法(QGA)[21]和Q(λ)算法[16]做比较分析。
4.1 仿真模型
本文采用的IEEE 118节点系统作为仿真模型含有54个机组和186条支路,根据《2006年IPCC国家温室气体清单指南》[22],可确定各机组碳排放强度如表1所示。选定的可控变量是节点45、79、105的无功补偿容量和线路 8-5,26-25,30-17,63-59,64-61的有载调压变压器分接头位置。其中无功补偿容量分成5档,分别对应正常值的 -40%、-20%、0%、20%、40%,有载调压变压器变比分成3档,分别0.98(p.u.)、1.00(p.u.)、1.02(p.u.)。则动作空间总共有5×5×5×3×3×3×3×3=30375个动作,不等式约束的个数为:54+1+64=119,分别对应发电机无功出力、发电机平衡节点有功出力和负荷节点的电压。

表1 IEEE118节点机组碳排放强度/δgwTab.1 Carbon emission intensity of IEEE 118 bus
经过大量的仿真分析,本文算法中的参数设置如下:
(1)学习因子c1取0.18,学习因子c2取1.2;
(2)折扣因子γ取0.49,资格迹衰退系数λ取0.3,学习速率α取0.1,动作搜索速度β取0.5;
(3)目标函数的权重系数μ1和μ2都取1/3,群体个数取为20。
4.2 算例分析
图3给出了Q(λ)算法和PSO-Q(λ)算法时的Q值收敛过程。由图3(a)可以看出,Q(λ)算法在经历一系列的试错和探索后可以收敛到最优Q*矩阵,但是收敛时间很长。PSO-Q(λ)算法能够在很短的时间内就收敛,寻优速度明显快于Q(λ)算法,如图3(b)所示。

图3 Q值收敛过程Fig.3 Convergence process of Q-value
图4给出了PSO-Q(λ)算法时的收敛过程。从图中可以发现:(1)所有个体的动作(即控制变量)在迭代50步左右即可趋于一致;(2)所有个体最终收敛得到的变量为最优变量,使得目标函数值达到最小。

图4 PSO-Q(λ)算法收敛过程Fig.4 Convergence process of PSO-Q(λ)

表2 不同算法下的最优碳-能复合流结果统计表Tab.2 OCECF statistical results in different algorithms
为了进一步比较PSO-Q(λ)算法和其他几种算法的性能,表2给出各个算法在同一断面下运行10次得到的优化结果平均值。从仿真结果可以看到:(1)遗传和量子遗传算法的收敛速度相对更快,在20 s左右即可收敛,但是算法容易陷入早熟,收敛到局部最优解;(2)Q和Q(λ)算法由于遍历了马尔科夫过程,具有较强的全局收敛性,然而其收敛时间长达10 min左右,当电网规模增加时,就难以满足OCEEF的在线动态滚动优化要求;(3)PSO-Q和PSO-Q(λ)算法虽每次都收敛到全局最优解,但其所得的目标函数值明显优于遗传和量子遗传算法,其收敛时间不超过1 min,明显快于单主体Q和Q(λ)算法,可以满足最优碳-能复合流的在线滚动优化。(4)在引入资格迹后,与Q算法和PSO-Q算法相比,Q(λ)算法和PSO-Q(λ)算法的收敛时间分别加速了 8%和9%。
表3统计了各种算法10次优化运行的收敛性能。可以发现:(1)Q和Q(λ)算法具有很强的全局寻优鲁棒性,算法每次都能收敛到最优解,收敛值的方差和标准差均为零;(2)遗传和量子遗传算法每次的收敛结果都不一样,容易较早收敛到局部最优解;(3)PSO-Q和PSO-Q(λ)算法10次仿真中分别有7、8次收敛到最优解,相对于遗传和量子遗传算法收敛鲁棒性更强,目标函数值的方差和标准差更小。

表3 不同算法下的运行收敛性能统计表Tab.3 Statistical results of convergence metrics in different algorithms
5 结束语
本文研究了电网能流与碳流复合模型,提出了一种基于真正群智能强化学习的电网碳-能复合流多目标优化方法,理论创新性贡献归纳如下:
(1)有机结合了电网能流和碳排放流传输特性,首次提出了电网最优碳-能复合流的概念,并采用多主体强化学习 PSO-Q(λ)算法来有效地解决OCECF问题;
(2)在传统单主体Q(λ)算法的基础上,结合了群智能优化方法,大大提高了传统Q(λ)算法寻优的速度,更加符合实际大规模复杂电网的碳-能复合流在线滚动优化实时性要求;
(3)与传统Q(λ)算法一样,群智能强化学习算法的收敛稳定性高,能更高效地找到碳-能复合流的全局最优解,能在保证电压安全稳定的同时,有效降低电网的碳流损耗和有功功率损耗。很显然,本文所提的新优化算法也可以推广到其它电力系统多目标优化问题的求解中去。

