能源互联网下商业楼宇能量管理优化算法*

郑宇，赵俊华，董朝阳，王德志，潘振宁，李正佳

（1.南方电网科学研究院，广州510080；2.苏州华天国科电力科技有限公司，江苏苏州215000）

0 引 言

随着世界能源的不断消耗，传统的石油能源十分紧缺，同时伴随着各类新能源的开发和信息技术的发展，全球的能源格局正在从以往的单一能源供应走向分布式小能源与集中式大能源共同供应的能源互联网模式。在这种模式下，电力网、天然气网络等能源网是能源互联网的重要组成部分，通过多能流的互相融合使用，能够使得能量管理变得更为可靠和灵活［1-2］。

在能源互联网下的需求侧，工商业用户是电力消费的重要成分。工商业负荷具有总量大，用电规律和具有十分可观的需求响应潜力的特点。研究工商业的能量管理，能够将能源侧与需求侧结合起来，通过工商业负荷的需求响应，不仅能够有效优化电网的负荷曲线，达到削峰填谷的效果，而且能够给予工商业用户一定的补贴，减轻其在能源方面的费用支出。

由于商业负荷多为大量集中的照明负荷、空调负荷等，在不影响商业运营的前提下，集中式的控制手段与调节方式更为灵活多样，还能够减少对电网造成的冲击，是需求响应实施的理想用户［3］。而工业用户由于其生产线及相关生产设备不能频繁开关，从而其可调性不如商业用户来得灵活。商业负荷是区域用电负荷的重要组成部分，由于商业用户的高度集中，使得商业负荷呈现高密度的特点，相比于分散的社区与家庭负荷，商业负荷能够实现集中的控制与调节，基于电价与激励报酬的需求侧响应更容易实现，经济效益更为客观［4-5］。因此，本文以综合商业楼宇负荷与多种能源为研究对象，考虑多能源融合的能源供应模式，建立商业楼宇能量管理（commercial building energymanagement，CBEM）优化模型，以商业楼宇的舒适度和经济性为目标函数，同时考虑在分时电价机制下其主动通过储能装置来进行负荷转移抑制负荷曲线波动［6-7］。最后利用灰狼优化算法［8］（grey wolf optimizer，GWS）对某市某综合商业楼宇的模型进行求解仿真。

1 CBEM模型

在CBEM模型中，综合商业楼宇用电主要包括制冷系统、供热系统、照明系统、动力系统、办公设备及其他用电。其中照明系统、动力系统、办公设备及其他用电与季节没有太大相关性，因此认为其电负荷全年基本稳定，但空调系统和供热系统作为与人体舒适度相关的重要设备，其负荷与季节和温度有十分紧密的联系。在本文所提的综合商业楼宇中，还包括了储能系统和冷热电联产（combined cool、heat and power，CCHP）系统，其中CCHP与储能装置作为电力生产与储存的装置，与电网配合供电；热能供给系统主要由CCHP的余热供给。因此，本文的CBEM是一个多能源融合的能量管理模型，其框架图如图1所示。

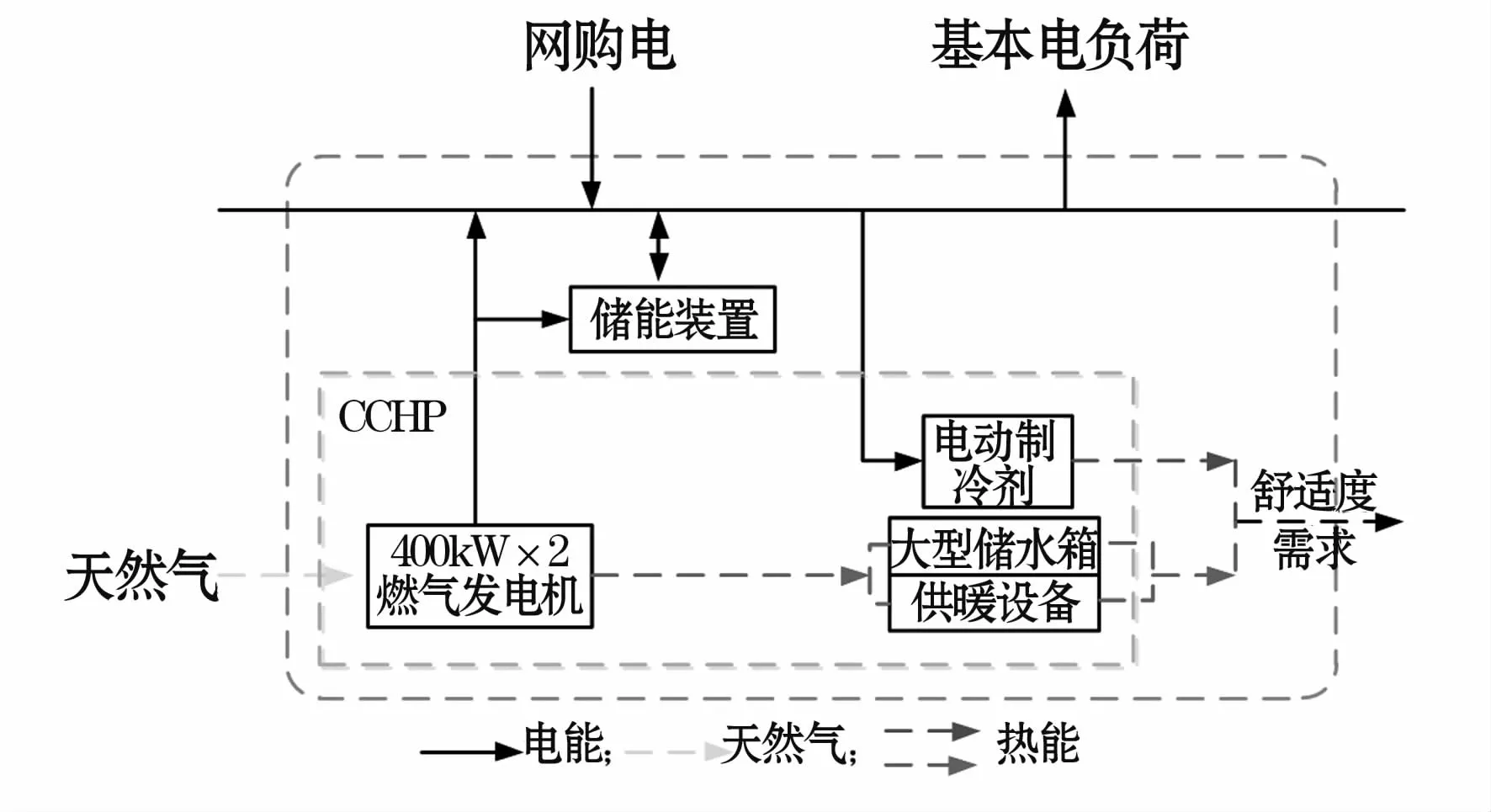
图1 CBEM框架图Fig.1 Framwork of CBEM

本文所提的CCHP的工作原则是以热定电，根据当前时刻的商业楼宇所需热负荷，通过燃气发电机与热回收装置来提供所需的热能与一定比例的电能［1］。基于该种工作模式，楼宇所需的电负荷由电网、CCHP与储能系统协调配合供给，其基本原则为：楼宇电负荷优先由CCHP提供的电能满足，不足的电量则通过电网供电；若CCHP提供的电能有所富余，则通过储能装置进行存储电能；储能系统则根据CCHP的工作状态与当前总负荷量与电价信息，确定其充放电状态。储能系统在商业楼宇能量管理系统中起到了转移负荷的作用。

2 CBEM组件模型

本文的CBEM模型由基本负荷、室温调节负荷、热水负荷以及储能系统与燃气发电机等组件组成。其中基本负荷由照明系统、动力系统、办公设备及其他电负荷基本稳定的部分组成，在考虑电价激励的管理策略下，其基本不受电价波动影响。

2.1 室温调节负荷模型

商业楼宇的室温调节负荷需将室内温度控制在满足用户舒适度的范围内。根据能量守恒定理可知，单位时间内室内空气从室外吸收的热量为：

式中Qt为t时刻室内从室外吸收的热量；和分别为t时刻室外和室内的温度；R为房屋热阻。

在制冷机工作时，其从室内吸收热量从而降低室内温度，室内的温度变化为：

其离散化表达式为［9］：

在供暖时，由CCHP提供热量，室内的温度变化为：

其离散化表达式为：

2.2 热水负荷模型

热水负荷考虑为储水箱，其主要为了使水箱储存的热水随时能够处于用户可接受的温度范围内，并假设当热水被消耗后，会立即有等量冷水注入。根据热力学第二定律，可得到水温的表达式为［10］：

2.3 储能模型

本文考虑的储能模型为蓄电池组，并假设其△t时段内充放电功率恒定，以其荷电状态（state of charge，SOC）作为评估变量，其充放电模型数学表达式为［11］：

式中SOCt为t时刻的蓄电池荷电状态；和为蓄电池t时刻的充放电功率；δch和δdch分别为充放电效率；Bbatt为蓄电池容量。

同时，考虑蓄电池不工作时，会产生一定的静态损耗，本文考虑1%／小时的静态损耗。

2.4 CCHP模型

CCHP集成了发电、制热、制冷等功能，其输出的电功率和热功率满足［1］：

3 多目标CBEM优化模型

3.1 目标函数

CBEM优化模型以商业楼宇的舒适度及支出费用成本作为目标函数。其中舒适度目标即楼宇的室内温度能够控制在人体可接受范围内，本文以实际温度与人体最舒适温度的差值最小为舒适度目标函数；而支出费用成本函数则包括了电网购电费用及天然气消耗费用，本文以两者费用之和最小为经济性目标函数，两个目标函数可表达如下：

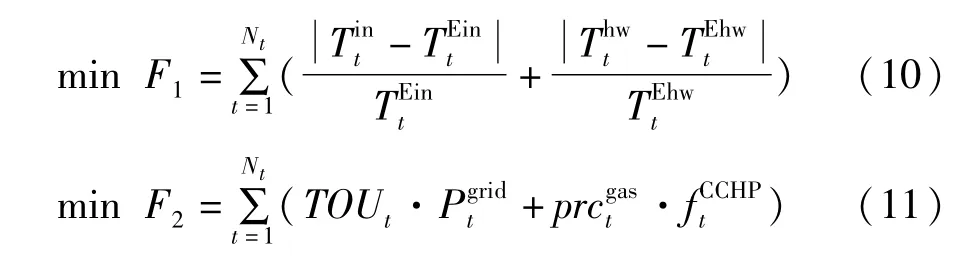
3.2 约束条件

（1）电力有功功率平衡

电力能量交换需满足能量守恒定律，即：

式中Pe为电负荷功率之和。

（2）室温调节负荷和热水负荷约束

室温调节系统与储水箱需分别满足功率约束与舒适度约束如下：

（3）储能充放电功率约束

考虑到安全因素，蓄电池充放电功率须时刻控制在安全范围之内，并且其SOC不能低于一定的值：

（4）CCHP运行约束：

当室温调节系统处于制热时，CCHP除了为储水箱提供热功率外，还为室内供暖提供了热功率其需要满足能量守恒定律，即：

此外，CCHP工作与以热定电模式，其输出的电功率与热功率还需满足以下关系：

4 CBEM模型求解算法

本文采用GWO算法来求解上述CBEM优化模型。GWO算法是Seyedali Mirjalili等人受狼群社会组织和捕猎策略行为启发而提出的群搜索智能算法。该算法将每个解视作一匹狼，最优解视作“猎物”，以“狼群”为依托对猎物进行搜索捕食，借鉴狼群社会的等级制度对各解进行分级，参照狼群捕食时的包围策略和进攻策略确定各解的位置和搜索方向，从而得到最优解。GWO算法中，每一个解视作一匹狼，将每轮迭代适应度最好的解设为α狼，次优和第三优的解分别设为β狼和δ狼，其余解皆为ω狼。α、β和δ共同领导狼群的行进方向并找出最优解。GWO算法流程图如图2所示。

图2 灰狼优化算法流程图Fig.2 Framwork of CBEM

5 算例分析

5.1 仿真参数设置

对南方某市某栋综合商业楼宇在夏季与冬季的典型日进行仿真分析。假设该市商业电价采用分时电价机制，其电价曲线如图3所示。天然气价格为3.6元／m3。储水箱及室温调节系统的相关参数设置如表1所示，CCHP的相关参数设置如表2所示，储能系统的相关参数设置如表3所示。本文优化时间尺度为Δt＝1 h，仿真时间一天24小时。

图3 商业分时电价曲线Fig.3 Commercial TOU curve

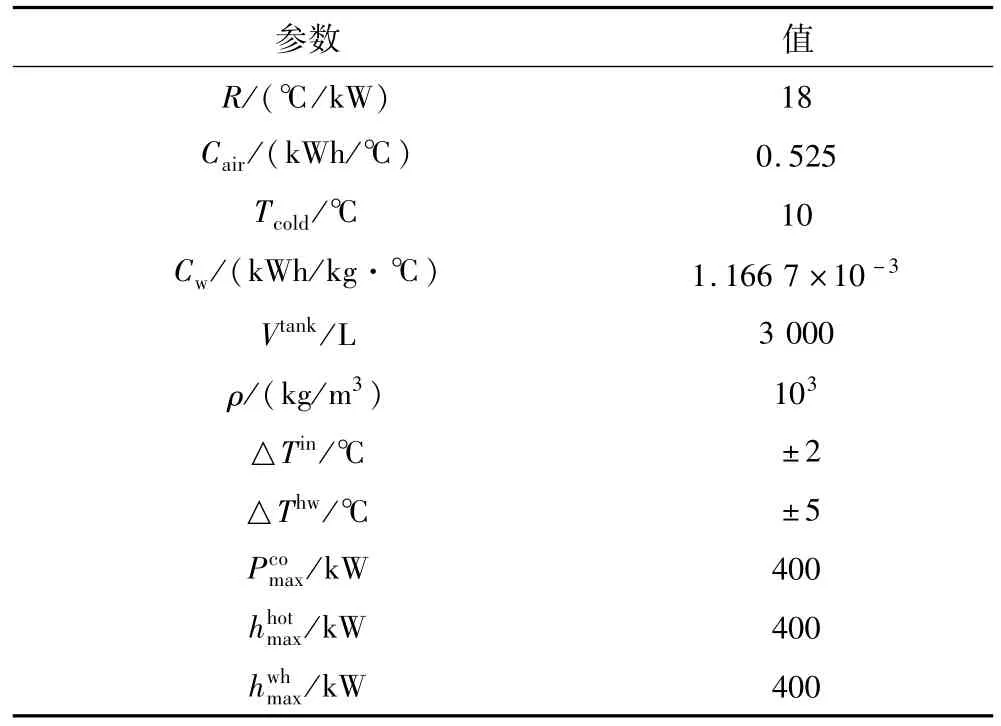
表1 储水箱及室温调节系统的相关参数设置Tab.1 Parameter setting ofwater tank and room temperature regulation system

表2 CCHP相关参数设置Tab.2 CCHP related parameter settings

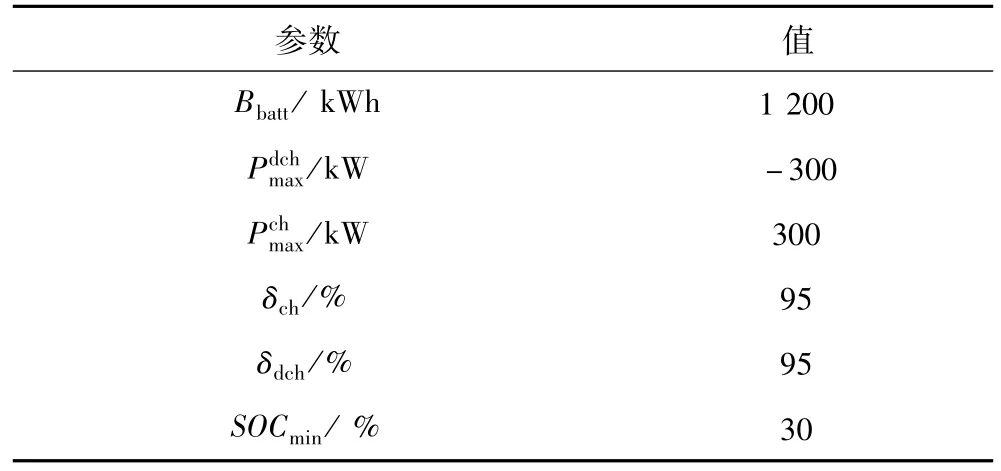
表3 储能系统相关参数设置Tab.3 Parameter setting of energy storage system

5.2 仿真结果比较分析

在夏季典型日中，综合商业楼宇中供暖系统不会启用，故CCHP产生的热功率仅供热水负荷使用。由图4可知，一天24小时内，该楼宇的室内温度基本能够维持在23℃上下，而热水温度则由于热水的使用，冷热水混合而导致其温度在45℃上下波动。两者均能够满足式（13）、式（14）的温度约束条件。由图5可知，楼宇的电负荷主要由基本负荷与制冷负荷组成，其电能来源包括CCHP出力、储能出力与网购电。由于楼宇的电负荷量大，而CCHP与储能装置由于其出力及容量限制，大部分电负荷还是需要由网购电来满足，但由于CCHP与储能装置的配合，从图5中可以看出，楼宇电负荷曲线能够有效的进行负荷转移，尤其是在分时电价的激励下，储能装置能够有效地通过高电价放电、低电价充电的方式来降低整体电费支出，假如所有电负荷及热负荷均有电网供电，其电费支出需20 628元，而在当前条件下，由表4可知，电费加燃气费总共为19 295元，从而使得楼宇的能源费用支出减少。由表4可以看出，夏季总负荷曲线标准差值为383.28 kW，而电网供电曲线标准差值为319.66 kW，由此可以看出，由于CCHP与储能装置的加入，使得电网的负荷曲线波动程度得到一定的抑制。图6是CCHP的热功率、电功率及天然气消耗速率曲线，由于夏天无暖气需求，该热功率全部用来加热热水，并由于CCHP工作于“以热定电”的模式，从而其电功率曲线与天然气消耗曲线与热功率曲线一致。CCHP的加入使得天然气燃烧产生的热能得以利用，在一定程度上实现了电气转化的效果。

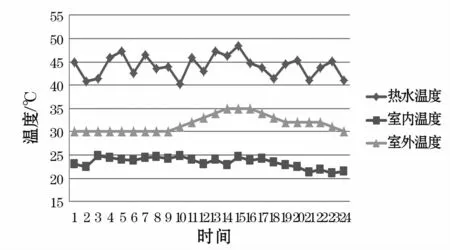
图4 热水温度及室内外温度曲线（夏季）Fig.4 Hotwater temperature and indoor and outdoor temperature curves（Summer）

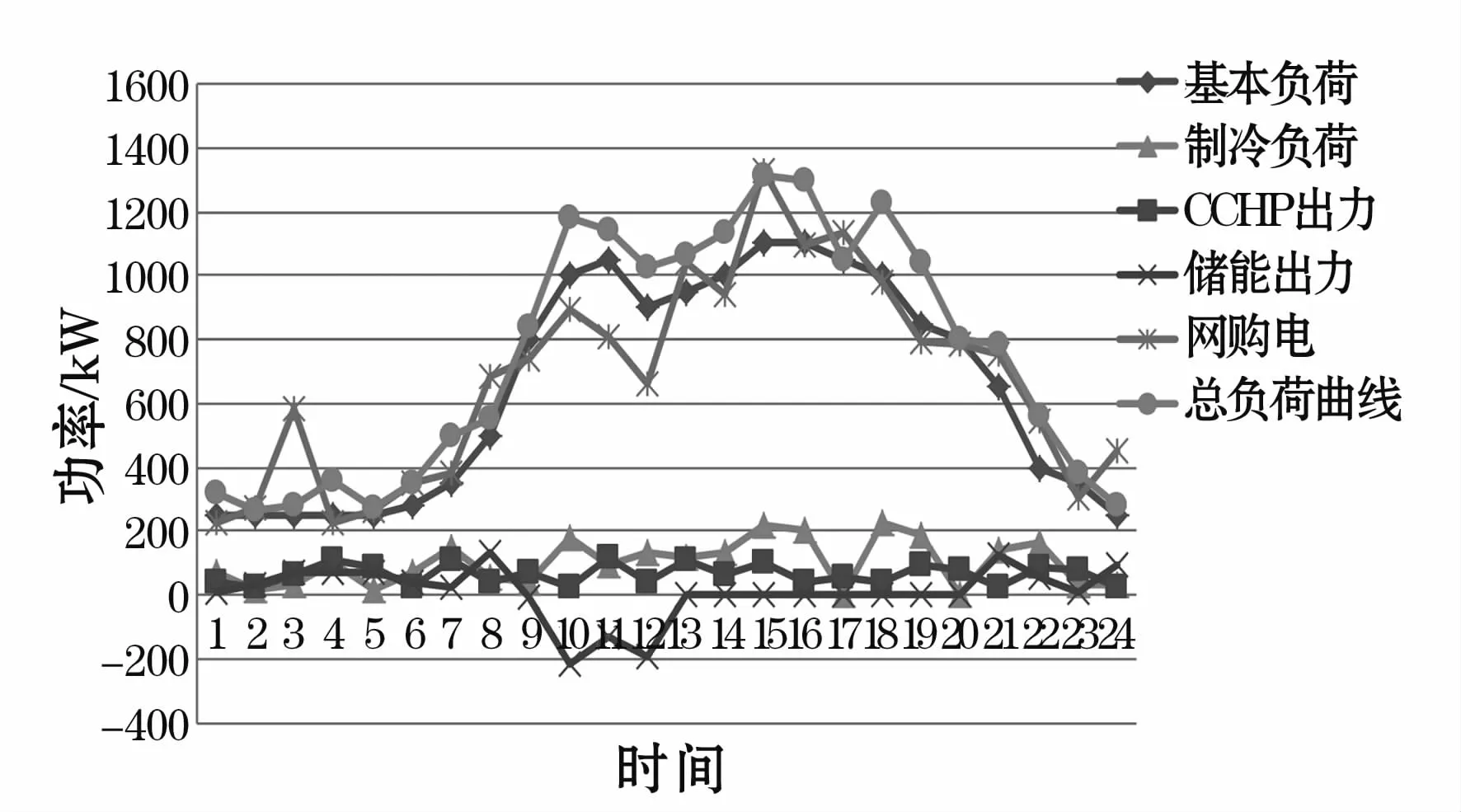
图5 负荷及出力曲线（夏季）Fig.5 Load and output curve（Summer）

在冬季典型日中，由于室外气温相对较低，因此综合商业楼宇启用供暖系统，与此同时制冷系统关闭，且供暖系统所需的热功率和热水负荷均有CCHP产生的热功率提供。由图7可知，冬季由于室外温度较低，室内温度基本能够维持在22℃上下；而由于冬季热水使用量较大较频繁，热水温度维持在相对较低的水平，在41℃上下波动，但也能够满足式（14）的温度约束条件。从图8可以看出，相比于夏季，CCHP的热负荷出力增长了2～3倍，并且其电能出力及天然气消耗速率也相对提高了2～3倍。从图9可以看出，冬季与夏季的基本负荷相同，这是因为该部分用电设备的使用与季节基本无关，因此其负荷曲线在本文中假设不变。同时，由表5可知，冬季的电网负荷曲线与楼宇负荷曲线相比，其标准差降低了约40 kW。

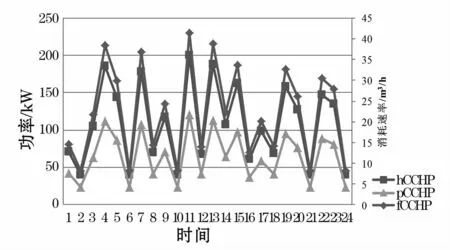
图6 CCHP输出热功率、电功率及天然气消耗速率曲线（夏季）Fig.6 CCHP output thermal power，electrical power and natural gas consumption rate curve（Summer）

图7 热水温度及室内外温度曲线（冬季）Fig.7 Hotwater temperature and indoor and outdoor temperature curves（Winter）

为了比较本文所用GWO优化算法的效果，加入了遗传算法（Genetic Algorithm，GA）［12］与粒子群算法（Particle Swarm Optimization，PSO）［13］两种典型优化算法进行比较，其比较结果如表4和表5所示。从两个表格中可以看出，GWO的优化结果，商业楼宇的电费与燃气总支出低于GA与PSO的优化结果。而在通过负荷转移来抑制负荷曲线波动的效果上，GWO同样具有一定的优势。综上所述，本文所选GWO优化算法对于求解CBEM模型具有良好的效果。

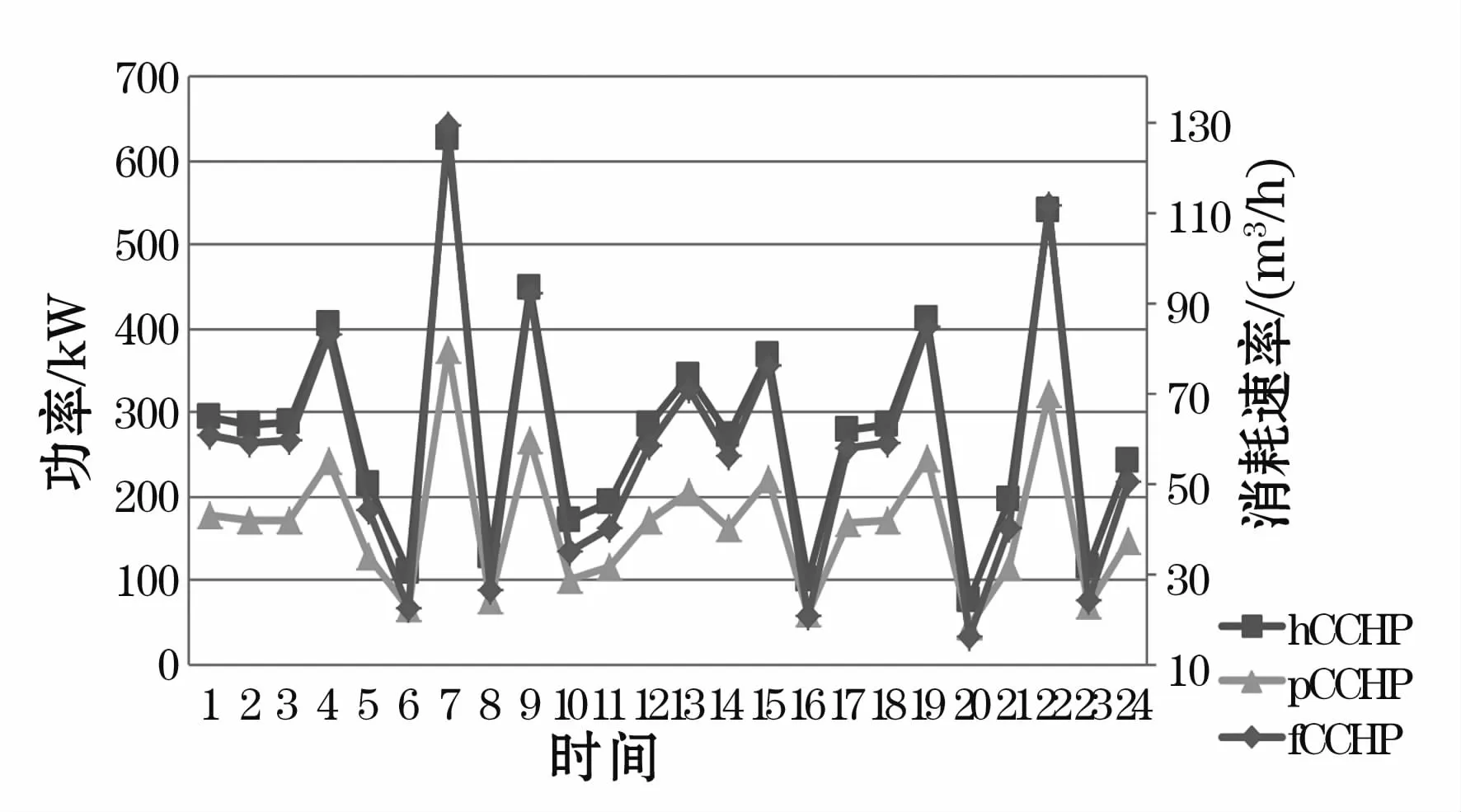
图8 CCHP输出热功率、电功率及天然气消耗速率曲线（冬季）Fig.8 CCHP output thermal power，electrical power and natural gas consumption rate curve（Winter）

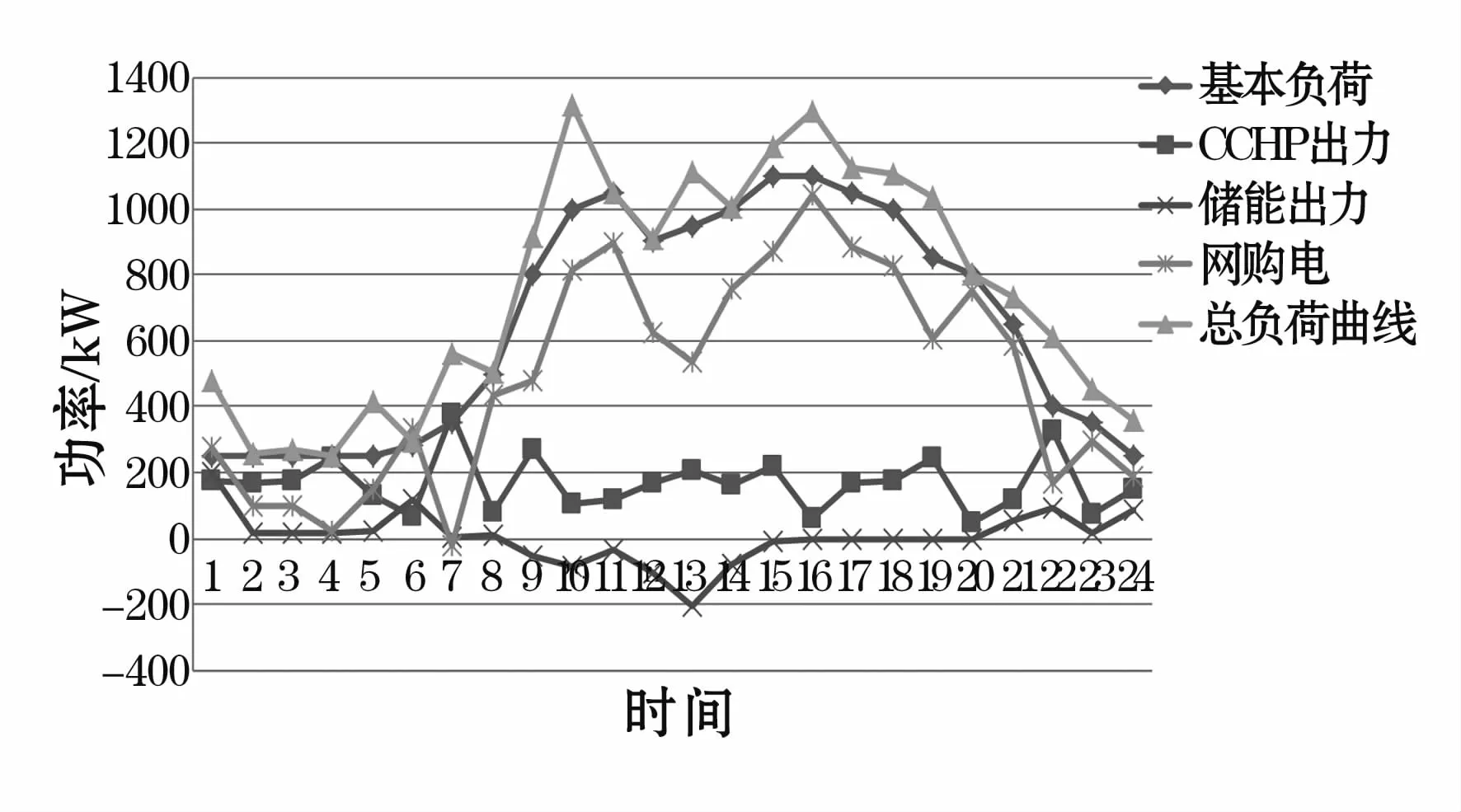
图9 负荷及出力曲线（冬季）Fig.9 Load and output curve（Winter）

表4 算法效果对比（夏季）Tab.4 Comparison of algorithm results（Summer）

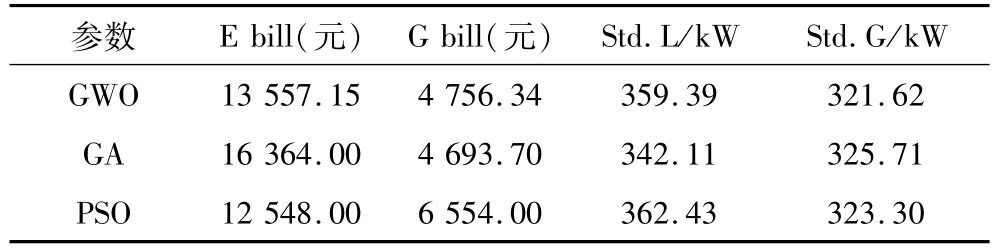
表5 算法效果对比（冬季）Tab.5 Comparison of algorithm results（Winter）

6 结束语

在能源互联网的背景下，提出了一种商业楼宇能量管理优化模型，该模型具有多能源融合的特点，并考虑了在分时电价机制下，CCHP与储能装置的协调配合策略。由GWO求解CBEM模型的仿真结果可知，该模型能够有效满足楼宇舒适度的需求，同时能够降低商业楼宇在能源费用的支出。