U(Ⅳ)对Pu(Ⅳ)的单级还原反萃数学模型

于 婷，何 辉，洪 哲，陈延鑫，叶国安,*

1.中国原子能科学研究院 放射化学研究所，北京 102413；2.环境保护部 核与辐射安全中心，北京 100082；3.中国核工业研究生部，北京 102413

U(Ⅳ)对Pu(Ⅳ)的单级还原反萃数学模型

于 婷1，何 辉1，洪 哲2，陈延鑫3，叶国安1,*

1.中国原子能科学研究院 放射化学研究所，北京 102413；2.环境保护部 核与辐射安全中心，北京 100082；3.中国核工业研究生部，北京 102413

U(Ⅳ)是PUREX流程铀钚分离过程的还原剂。建立了30%TBP/煤油体系中U(Ⅳ)还原反萃Pu(Ⅳ)的单级迭代计算数学模型，并提出了相应的数学算法，编写了模拟连续逆流萃取器其中一级的计算机模拟程序，使用文献数据对模型和程序进行了验证，计算值与实验值符合良好，并与文献报道的模型的计算结果进行了比对，准确度要高于文献数学模型。

PUREX流程；计算机模拟；还原反萃；U(Ⅳ)；Pu(Ⅳ)

核燃料后处理是实现核材料闭式循环的重要环节。通过后处理分离得到的钚以及其他锕系元素制成燃料后，再次在反应堆中燃烧或者嬗变处理，不仅可以支持核能的可持续发展，还可以降低需要长期地质储存的放射性废物的放射性强度和体积[1]。当前世界各国采用成熟的溶剂萃取PUREX流程。该流程是复杂的多级逆流萃取流程[2]，其中铀钚分离工艺单元(1B)是整个流程的分水岭，其运行工况对后续的工艺单元有重要的影响作用。铀钚分离是通过使用合适的还原剂将Pu(Ⅳ)还原成为Pu(Ⅲ)，因为Pu(Ⅲ)在有机相(30%(体积分数，下同)TBP/煤油)和水相中的分配系数非常低，基本不被有机相萃取，从而将钚反萃到水中，U(Ⅵ)继续保留在有机相中从而实现了铀钚分离[3]。20世纪60年代以前，国外大型后处理厂一般采用氨基磺酸亚铁作为Pu(Ⅳ)的还原剂，但氨基磺酸亚铁会引入铁离子，使废液中盐分增大而不利于废液浓缩处理，而且产生的硫酸根离子会加剧设备的腐蚀。因此在20世纪60年代以后在1B工艺单元使用U(Ⅳ)取代氨基磺酸亚铁，其优点是在流程物流中不会引入非挥发性物质，且U(Ⅳ)可被TBP萃取，比较容易将它从钚液流中去除以满足对铀净化的要求，并且不会给铀产品引进杂质[3-4]。与钚反萃工艺单元(2B)使用的还原剂硝酸羟胺(HAN)对钚的还原反萃不同的是，U(Ⅳ)对Pu(Ⅳ)的氧化还原反应在水相和有机相同时进行，在不同介质中的氧化还原反应化学方程式相同，但反应速率不同。

此外，国外近几十年来对PUREX流程的计算机模拟做了大量的研究工作，以美国、法国及日本等国为代表开发了大量的后处理模拟程序，但基于商业应用软件保护的目的，数学模型及软件细节鲜见报道[5-16]。在PUREX流程模拟软件中，U(Ⅳ)对Pu(Ⅳ)的还原反萃模型是铀钚分离工艺单元(1B)模拟研究的基础。以往对于U(Ⅳ)对Pu(Ⅳ)的还原反萃的模拟按照模型考虑的化学反应可以分为两类：一类是只考虑水相中U(Ⅳ)对Pu(Ⅳ)的还原反应，主要以美国橡树岭国家实验室的SEPHIS-MOD4为代表[6]；另一类则是同时考虑水相和有机相中的氧化还原反应，主要以日本东海研究所的MIXSET系列软件[12-13]和日本原子能研究所的EXTRA·M[10]为代表。此外还可以按照单元模型中对于分配比计算模块和氧化还原反应模块的组合方式分类：第一类认为反应仅在水相中发生反应，有机相中的有效组分Pu(Ⅳ)为水相中化学反应的缓冲剂，即认为有机相中的组分也参与了水相中的氧化还原反应，模型计算时首先通过物料守恒方法将有机相中的组分归一化至水相中，然后使用氧化还原反应动力学模型进行氧化还原反应的计算，最后使用分配比模型进行传质计算(分配平衡计算)，这类仍主要以SEPHIS系列为代表；第二类认为U(Ⅳ)对Pu(Ⅳ)的氧化还原反应在水相和有机相中同时进行，因此在单级模型中先进行传质反应计算，调用分配比模块，因为该体系中的相关组分在两相的传质速度较快，则认为传质平衡瞬间完成，然后调用氧化反应动力学模块对水相和有机相中的反应进行计算，其中第一类计算反应的依据是水相和有机相同时进行反应，且传质速率极大，但是因为两相中化学反应速率相差20倍之多[5]，先将有机相中的组分归一化至水相再化学反应计算，这类方法较实际情况对化学反应的计算程度偏大；第二类模型忽略了有机相中的Pu(Ⅳ)在氧化还原反应进行同时、会因浓度的降低而逐渐向水相传质的情况，这样势必对氧化还原反应的计算程度较实际情况偏小。SEPHIS和EXTRA·M软件尽管对氧化还原反应和分配反应的考虑方式不同，但共同点是均未将氧化还原反应和传质反应作为动态且相互影响的耦合化学过程考虑，这些出于计算方便的假设与实际情况存在一定的偏离。

U(Ⅳ)对Pu(Ⅳ)的还原反萃是一个复杂的反应过程，该过程涉及水相中U(Ⅳ)和Pu(Ⅳ)发生的氧化还原反应以及U(Ⅳ)在水相中被硝酸氧化，以及有效组分Pu(Ⅳ)、Pu(Ⅲ)、U(Ⅵ)、U(Ⅳ)和HNO3等在两相间的传质分配反应。本研究从30%TBP/煤油体系中U(Ⅳ)对Pu(Ⅳ)的还原反萃过程的实际出发，综合考虑传质反应和氧化还原反应，建立1B过程单级还原反萃模型，并提出数学算法，使用Visual Basic6.0语言编写了连续逆流萃取器其中一级的计算机模拟程序，作为1B工艺单元计算机模拟程序的基础模块，并使用文献报道的数据对模型进行验证。

1 U(Ⅳ)对Pu(Ⅳ)的还原反萃过程

铀钚分离工艺单元采用U(Ⅳ)作为还原剂将Pu(Ⅳ)还原成为分配系数较低的Pu(Ⅲ)，使其从有机相进入水相，而铀仍存在于有机相中，从而实现铀钚分离。有研究认为U(Ⅳ)使Pu(Ⅳ)被还原反萃到水相的过程主要是由以下过程构成的：① U(Ⅳ)进入到有机相；② 部分Pu(Ⅳ)进入到水相中；③ 有机相中的Pu(Ⅳ)被还原成Pu(Ⅲ)后转入到水相；④ Pu(Ⅳ)在有机相和水相中均可被还原成为Pu(Ⅲ)而进入水相中。其中过程①—③为传质反应，过程④为氧化还原反应过程[3]，具体过程示于图1。

因为还原剂U(Ⅳ)在水相和有机相中分布，显而易见，氧化还原反应同时在水相和有机相中进行。在水相中U(Ⅳ)易被HNO3氧化，该过程生成HNO2，而生成的HNO2则会快速的被水相中的N2H4反应掉[3,10,12]，因反应速率较快，可以认为是瞬间反应，因此水相发生的主要化学反应为：

图1 U(Ⅳ)对Pu(Ⅳ)的还原反萃过程Fig.1 Reductive stripping of Pu(Ⅳ) with U(Ⅳ)

(1)

(2)

(3)

有机相中主要发生的化学反应为U(Ⅳ)对Pu(Ⅳ)的氧化还原反应，方程与式(1)相同[10,12]。

因U(Ⅳ)将Pu(Ⅳ)还原成分配比较低的Pu(Ⅲ)，将钚反萃进入到水相中，水相中发生的氧化还原反应速率是有机相中的23倍之多[10,12]，因此氧化还原反应的进行总体使得水相中的Pu(Ⅳ)的浓度降低，从而打破了Pu(Ⅳ)在两相中的分配平衡，使得以下平衡逐渐向右移动，最终实现了钚的还原反萃：

(4)

式中下标o和a分别代表有机相和水相。

此过程中涉及的两相中发生的氧化还原反应与有效组分在两相间的传质反应同时进行，相互影响，是一个非常复杂、动态的耦合化学过程。

2 U(Ⅳ)对Pu(Ⅳ)的还原反萃数学模型

如前文所述，先前的研究者对U(Ⅳ)对Pu(Ⅳ)的还原反萃过程模拟可以分为两种：第一种以SEPHIS-MOD4为例[6]，将有机相中的组分归一化到水相中，然后使用氧化还原反应动力学模型对氧化还原反应程度进行计算，采用二分法对反应模型进行求解，之后对反应后的有效组分使用分配比模型对其在两相中的分配重新计算，该体系中有效组分在相际间的传质速率是氧化还原反应速率的几百倍，则认为两相液体的停留时间为化学反应时间，分配平衡为瞬间达成；第二种计算方法以EXTRA·M[10]为代表，在单级模型中首先使用分配比模型对有效组分在两相间的分配进行计算，之后使用氧化还原反应动力学模型对水相和有机相中U(Ⅳ)对Pu(Ⅳ)的氧化还原反应进行计算，使用四阶龙格-库塔方法对反应模型进行求解与第一种计算方式类似，同样假设停留时间即为氧化还原反应时间，分配平衡为瞬间完成。这两类模型对氧化还原反应进行动态计算，但并未从实际的还原反萃过程出发，即两相间发生的反应与组分的传质分配同时进行相互影响，故两种模型对整个动态过程的计算偏大或偏小。

基于U(Ⅳ)对Pu(Ⅳ)还原反萃过程的实际情况，建立的数学模型综合考虑到了两相中的氧化还原反应和传质分配且相互影响的实际，综合考虑氧化还原反应和分配反应，将其视为一个整体，具体模型示意图示于图2。

图2 还原反萃模型示意图Fig.2 Mathematical model of reductive stripping

2.1 U(Ⅵ)-U(Ⅳ)-Pu(Ⅳ)-Pu(Ⅲ)-HNO3-N2H4-30%TBP/煤油体系组分的分配比模型

在30%TBP/煤油体系中，金属元素以及HNO3等组分的萃取反应可以通过下式表达：

(5)

通常情况下，Mm+会形成M(NO3)m·nTBP络合物被萃入到有机相中，该反应的热力学平衡常数K可以用下式表达：

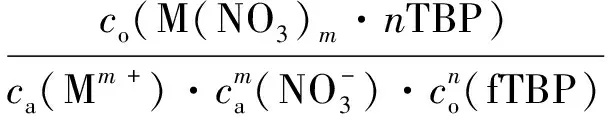
(6)

定义组分的分配比D为：

ca(M)=ca(Mm+)+ca(M(NO3)m-1)+

ca(Mm +)fM{ca(HNO3),T}

(7)

对上式加以变形可以得到：

D(M)=

(8)

式中：c表示组分的摩尔浓度，mol/L；γ表示活度系数；β为稳定常数；g和f表示函数；I为离子强度；T为温度，K；fTBP表示自由TBP，即未与M络合的TBP；下角标a和o分别表示水相和有机相。由通式可知TBP/煤油萃取体系中组分的分配比与萃取平衡常数K、总硝酸根浓度、自由TBP浓度以及相应的活度系数有关。

萃取反应平衡常数为温度的函数，温度一定时，K为常数，式(8)中所示组分的活度系数受体系中各种离子浓度的影响，对于TBP/煤油体系中各个组分在水相和有机相中活度系数的研究较少，缺乏相应的数据，因此很难按照式(8)和式(6)使用活度系数以及萃取平衡常数计算组分的分配比。现在各国对于PUREX流程的模拟采用的分配比模型均为经验模型，一般以Richardson等[17]的分配比模型为基础，Richardson引入了表观平衡常数K*，将K*拟合成为总硝酸根浓度和温度的函数，其中温度的影响主要以阿伦尼乌斯定律为基础，计算公式如下：

(9)

则组分Mm+的分配比D(M)可以用式(10)计算得到：

(10)

本工作采用的U(Ⅵ)-U(Ⅳ)-Pu(Ⅳ)-Pu(Ⅲ)-HNO3-N2H4-30%TBP/煤油体系组分的分配比模型以Richardson[17]、何辉[18]和陈延鑫[19]的相关研究为基础，在此需要说明的是，实际情况下Pu(Ⅳ)和U(Ⅳ)共存时会发生化学反应，不会稳定的共同存在，分配比模型研究对于化学反应不予以考虑，只考虑萃取反应部分，具体如下：

(11)

(12)

UO2(NO3)2·2TBPo

(13)

U(NO3)4·2TBPo

(14)

Pu(NO3)4·2TBPo

(15)

Pu(NO3)3·2TBPo

(16)

U(Ⅵ)、U(Ⅳ)、Pu(Ⅳ)、Pu(Ⅲ)和HNO3等组分的表观平衡常数关联成水相总硝酸根浓度和温度的函数，具体如下式：

(1 - 0.54e-15φ)e340τ

(17)

(18)

(19)

K*(U(Ⅳ))=

(20)

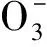
(21)

K*(Pu(Ⅲ))=0.011 38K*(Pu(Ⅳ))

(22)

(23)

则可根据各个组分的表观平衡常数计算得到以下分配比计算式：

(24)

D(U(Ⅵ))=K*(U(Ⅵ))·c2(fTBP)

(25)

D(U(Ⅳ))=K*(U(Ⅳ))·c2(fTBP)

(26)

D(Pu(Ⅳ))=K*(Pu(Ⅳ))·c2(fTBP)

(27)

D(Pu(Ⅲ))=K*(Pu(Ⅲ))·c3(fTBP)

(28)

以上各式中的c(fTBP)可以使用下式加以计算，其中c(TBP)=φ×3.651：

c(fTBP)=c(TBP)-2c(UO2(NO3)2·2TBPo)-

2c(U(NO3)4·2TBPo)-2c(Pu(NO3)4·2TBPo)-

3c(Pu(NO3)3·3TBPo)-c(HNO3·TBPo)

(29)

将以上各式对应的分配比计算公式代入式(29)则可计算得到自由TBP浓度和平衡水相中各萃取组分的关系式，如式(30)所示：

c(fTBP)=c(TBP)-3K*(Pu(Ⅲ))·

ca(Pu(Ⅲ))·c3(fTBP)-2K*(U(Ⅵ))·

ca(U(Ⅵ))·c2(fTBP)-2K*(Pu(Ⅳ))·

ca(Pu(Ⅳ))·c2(fTBP)-2K*(U(Ⅳ))·

(30)

若已知平衡水相中各组分浓度，则可以使用式(17)—(22)计算得到各组分的表观平衡常数，利用式(30)计算得到的c(fTBP)带入式(24)—(28)则可计算得到各组分的分配比以及平衡水相和有机相浓度。

2.2 氧化还原反应动力学模型

U(Ⅳ)对Pu(Ⅳ)的还原反萃过程涉及的氧化还原反应按照反应介质的不同可以分为水相中化学反应和有机相中化学反应[5,10,12]，其中水相中发生的氧化还原反应主要有：

动力学方程为：

(31)

动力学方程为：

(32)

动力学方程为：

(33)

有机相中主要发生的氧化还原反应如下：

动力学方程为：

(34)

2.3 还原反萃过程数学模型及算法

U(Ⅳ)对Pu(Ⅳ)的还原反萃过程是一个由水相、有机相氧化还原反应和相际间传质反应同时进行、相互影响的动态过程，将氧化还原反应和传质分配过程分开计算的数学模型势必会有较大的计算误差，本研究从萃取-氧化还原反应这一动态过程的实际出发，首先对提出的模型做以下假设：

(1) U(Ⅳ)与Pu(Ⅳ)的氧化还原反应在水相和有机相内部发生，两相界面不发生化学反应；

(2) 水相和有机相体积在氧化还原反应以及传质反应前后无变化；

(3) 水相和有机相在萃取单元内完全混合，两相充分接触传质；

(4) 组分在两相间的传质分配反应瞬间完成，达到平衡态。

含有氧化还原化学反应的多相平衡计算虽然仅比普通的相平衡的计算多了几组化学平衡方程的约束，但因为这些方程的约束，使得含有化学反应体系的相平衡的计算变得非常复杂，一般含有化学反应的体系的相平衡的计算大都从化学反应平衡的计算出发[20]。按照一般含有化学平衡体系多相平衡的计算方法，则对于还原反萃过程模拟的关键计算部分为式(31)—(34)的动力学方程求解，由动力学公式可知方程左边各个组分的浓度随着反应(1)—(3)的进行而变化，这类微分方程初值问题可采用四阶龙格-库塔方法求解[21]，具体如下：

(35)

K1=f(xn,yn)

(36)

(37)

(38)

K4=f(xn+h,yn+hK3)

(39)

在对式(31)—(34)的动力学方程求解时，式(35)—(39)中的h即为方程中的时间步长Δt，则t=n×Δt，式(35)—(39)计算一个时间步长的结果即这个Δt的氧化反应计算结果，此时调用分配比数学模型进行计算，计算结果作为下一个时间步长的计算输入，整个四阶龙格-库塔计算过程中嵌入分配比计算，化学反应-分配反应迭代计算n次的结果即为最终的还原反萃结果，一次四阶龙格-库塔计算需要计算五个方程式，则对于还原反萃时长t=n×Δt的计算需要计算5n次。

图3为还原反萃数学模型计算流程图。如图3所示，模型计算分为内外两层，在使用四阶龙格-库塔方法计算的每个时间步长中，内层计算为萃取分配平衡计算，使用Newton迭代方法求解，外层使用式(35)—(39)对一个时间步长的氧化还原反应求解。

3 软件编写

使用Visual Basic 6.0语言编写了U(Ⅳ)还原反萃Pu(Ⅳ)的单级模拟计算程序，所有的参数输入和结果输出均在图4所示的界面下完成，程序在Intel Core i5-5200U CPU 2.2GHz处理器、8.00 GB内存的电脑中调试通过。

图3 迭代模型流程图Fig.3 Flow sheet of iterative model

图4 单级计算程序参数输入输出图形界面Fig.4 Graphic interface for I/O of parameter

4 结果与讨论

4.1 模型验证

使用文献[22]公开报道的实验数据，以同等的实验条件作为U(Ⅳ)对Pu(Ⅳ)的单级还原反萃计算软件的参数输入，将程序的计算结果与实验数据进行了比对，从而完成了对程序的验证，计算结果列于表1，作为比较，表1中同时列出了文献[22]的实验值。

表1为于恩江等[22]的U(Ⅳ)对Pu(Ⅳ)的还原反萃实验数据与本研究计算值的比对，反应初始有机相钚质量浓度小于0.2 mg/L，其中计算的次数为10次(Δt×10=t)。则由表1所列数据可知，反应结束时水相总钚浓度(ρa,total(Pu)=ρa(Pu(Ⅳ))+ρa(Pu(Ⅲ)))的计算值与实验值符合良好。

表1 单级还原反萃实验值与计算值的比较Table 1 Comparison of Pu concentration calculated by single-stage model to experimental results

注：反萃前有机相钚质量浓度为6.91 mg/L；反萃剂为0.5 mol/L HNO3+0.1 mol/L N2H4；U(Ⅳ)/Pu(Ⅳ)物质的量比为5.7；相比O/A为1∶1；反应时间2 min

4.2 算法比对

对于U(Ⅳ)对Pu(Ⅳ)的还原反萃过程的模拟，对日本的EXTRA·M程序[10]的计算方法与本研究提出的算法的计算结果做了对比，如第2节所述，EXTRA·M程序首先对混合后的两相的传质分配进行计算，即首先调用分配比模型，之后分别对水相和有机相中的有效组分的氧化还原反应进行计算，二者计算结果即为反应时间为t的一级还原反萃的实验结果。本研究建立的模型认为两相传质分配和两相间的氧化还原反应是同时进行、相互影响的。图5和图6为一次传质分配-氧化还原反应模型的计算结果与迭代模型的计算结果的比对，图中横坐标分别为水相总钚浓度、有机相总钚浓度的实验值，纵坐标为水相总钚浓度、有机相总钚浓度的计算值，实线为斜率为1的比对线，点越在比对线聚集，则说明计算值和实验值符合愈良好。

由图5和图6可知，+表示的迭代数学模型对于单级钚的还原反萃过程的模拟计算结果要明显优于使用○表示的一次传质分配-氧化还原反应模型计算结果，后者对于水相的总钚浓度的计算相对误差集中在-70%～-30%之间，由此可知首先进行传质分配计算、然后再分别对两相进行氧化还原反应计算的模型，其计算得到的反萃进入水相中的总钚浓度均低于实际反萃进入水相中的总钚浓度，这表明此类模型对水相中氧化还原反应程度的计算小于实际值，即将传质分配和氧化还原反应视为独立静态的模型与实际情况有较大出入。本研究所建立的模型的相对误差多集中在1%以内，建立的钚的还原反萃单元数学模型要明显优于一次传质分配-氧化还原反应模型。

○ 表示一次分配-氧化还原模型计算值；+ 表示计算次数n=10、四阶龙格-库塔模型计算值；实线表示斜率为1的对比线图5 水相钚浓度计算值与实验值对比Fig.5 Comparison of Pu concentration in aqueous calculated by single-stage model to experimental results

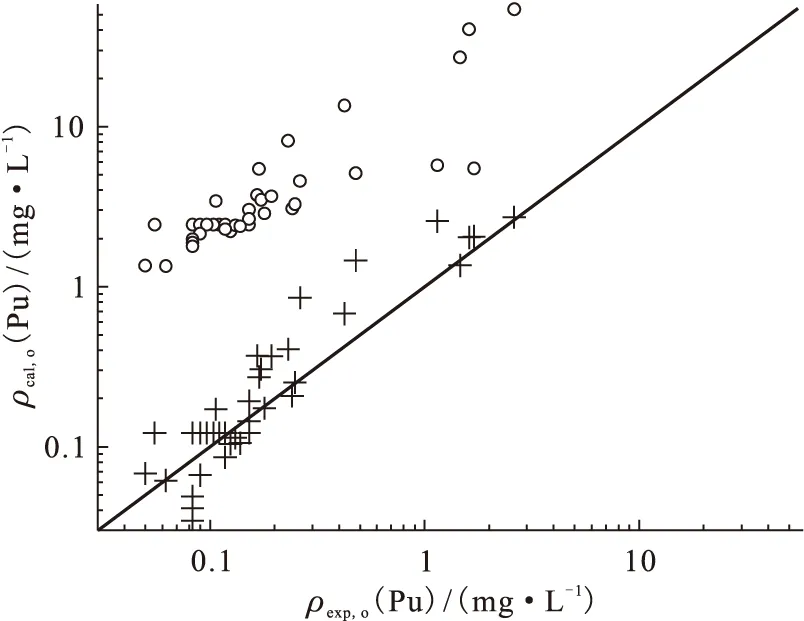
○ 表示一次分配-氧化还原模型计算值；+ 表示计算次数n=10、四阶龙格-库塔模型计算值；实线表示斜率为1的对比线图6 有机相钚浓度计算值与实验值对比Fig.6 Comparison of Pu concentration in organic calculated by single-stage model to experimental results

5 结 论

通过对U(Ⅳ)还原反萃Pu(Ⅳ)过程的分析，建立了基于迭代计算的U(Ⅳ)还原反萃Pu(Ⅳ)单元数学模型，使用Visual Basic6.0语言编写了计算软件，使用文献数据对数学模型和算法进行了验证，并与一次传质分配-氧化还原反应模型的计算结果进行了比对，可以得到以下结论：

(1) 基于化学反应-萃取反应耦合过程实际情况的U(Ⅳ)还原反萃Pu(Ⅳ)单元数学模型，模型外层使用四阶龙格-库塔方法计算氧化还原反应动力学模型，内层嵌入使用Newton迭代法求解的分配比模型，使用文献数据对所建立的模型进行了验证，水相总钚浓度的计算相对误差基本小于5%，计算值与实测值符合良好；

(2) 本研究模型计算结果与一次传质分配-氧化还原反应模型计算结果进行了比对，结果发现基于多次迭代的模型计算准确度远远高于一次计算模型。

因此，通过文献报道的数据对模型的验证可以得到，对于U(Ⅳ)还原反萃Pu(Ⅳ)单元所建立的数学模型，计算结果与实验值符合良好，计算准确度高，可以作为未来PUREX流程铀钚分离工艺单元计算机模拟程序的基础模块。

[1] 章泽甫,王俊峰,张天祥.动力堆核燃料后处理工学[M].北京：原子能出版社,2013.

[2] 陈延鑫，何辉，唐洪彬，等.后处理工艺Purex流程计算机模拟研究现状及展望[J].核化学与放射化学，2012，34(4)：193-200.

[3] 任凤仪,周镇兴.国外核燃料后处理[M].北京：原子能出版社,2006.

[4] Carl S S, Myron R C, Hugh E H, et al. Uranium(Ⅳ) nitrate as a reducing agent for plutonium(Ⅳ) in the PUREX, DP-808[R]. USA: Savannah River Laboratory, 1963.

[5] Suzuki A. Handbook on process and chemistry of nuclear fuel reprocessing, JAERI-Review 2001-038[R]. Japan: Japan Atomic Energy Research Institute, 2001.

[6] Mitchell A D. SEPHIS-MOD4: a user’s manual to a revised model of the PUREX solvent extraction system, ORNL-5471[R]. USA: OAK Ridge National Laboratory, 1979.

[7] Watson S B, Rainey R H. Modification of the SEPHIS computer code for calculating the PUREX solvent extraction system, ORNL/TM-5123[R]. USA: OAK Ridge National Laboratory, 1975.

[8] Scotton W C. SOLVEX: a computer program for simulation of solvent extraction processes, DP-1391[R]. USA: Savannah River Laboratory, 1975.

[9] Gonda K, Matsuda T. Calculation code PULCO for PUREX processes in a pulsed column, PNCT-841-82-19[R]. Japan: Power React and Nuclear Fuel Dev Corp, 1982.

[10] Tachimoli S. EXTRA·M: a computing code system for analysis of the PUREX process with mixer settler for reprocessing, JAERI-1331[R]. Japan: Japan Atomic Energy Research Institute, 1993.

[11] Tsubata Y, Asakura T, Morita Y. Development of a computer code PARC for simulation of liquid-liquid extraction process in reprocessing, JAEA-Data/Code 2008-010[R]. Japan: Tokai Works Power Reactor and Nuclear Fuel Development Corporation, 2008.

[12] Gonda K, Fukuda S. Calculation code MIXSET for PUREX process, PNCT 841-77-60[R]. Japan: Tokai Works Power Reactor and Nuclear Fuel Development Corporation, 1977.

[13] Gonda K, Oka K, Fukuda S. Calculation code revised MIXSET for PUREX process, PNCT 841-79-26[R]. Japan: Tokai Works Power Reactor and Nuclear Fuel Development Corporation, 1979.

[14] Naito M, Suto T, Asakawa K, et al. A computer code for simulating the PUREX solvent extraction process, JNC T8400-99-005[R]. Japan: Tokai Works Power Reactor and Nuclear Fuel Development Corporation, 1999.

[15] Christian S, Pascal B, Binh D, et al. The simple solution modeling implemented in the PAREX code to simulate solvent extraction operations[C]. Global, Chiba, Japan, 2011.

[16] Petrich G. The Purex process computer model “VISCO” and its application[C]. Proc Int Solvent Extraction Conf, Dechema, Munich, West Germany, Vol.1, 1986: 427.

[17] Richardson G L, Swanson J L. Plutonium partitioning in the PUREX process with hydrazine-stabilized hydroxylamine nitrate, Hanford Engineering Development Laboratory, HEDL-TME 75-31[R]. USA: OAK Ridge National Laboratory, 1975.

[18] 何辉，李高亮，陈辉,等.Purex流程共去污工艺计算机稳态模拟[J].原子能科学技术，2008,42(9)：769-784.

[19] 陈延鑫,何辉,彭力,等.Purex流程萃取体系下相关组分的分配比模型[J].核化学与放射化学,2014,36(2)：80-85.

[20] 林金清,李浩然,韩世钧.含化学反应体系多相平衡计算方法的研究进展[J].计算机应用化学,2003,20(6)：724-730.

[21] 李庆扬,王能超,易大义.数值分析[M].北京：清华大学出版社,2001.

[22] 于恩江,刘黎明,费洪澄,等.U(Ⅳ)作为Purex过程中Pu(Ⅳ)还原剂的研究[J].核化学与放射化学,1992,14(4)：207-214.

ComputerSimulationofSingle-StageReductiveStrippingofU(Ⅳ)WithPu(Ⅳ)

YU Ting1, HE Hui1, HONG Zhe2, CHEN Yan-xin3, YE Guo-an1,*

1.China Institute of Atomic Energy, P. O. Box 275(26), Beijing 102413, China; 2.Nuclear and Radiation Safety Center, Ministry of Environmental Protection of the People’s Republic of China, Beijing 100082, China; 3.Graduate Department of Nuclear Industry, Beijing 102413, China

U(Ⅳ) is the reductive agent of plutonium stripping unit(1B). The simulation of single-stage of 1B was studied in this paper. A new model and algorithm on reductive stripping of Pu(Ⅳ) with U(Ⅳ) from 30%TBP/OK was proposed, based on the iterative model. A computer program for simulating the single stage was developed. The data obtained from literature were compared with the model calculated data. In general, the experimental results seem to agree with the model, and the reliability and accuracy of the model proposed are better than the literature model.

PUREX; computer simulation; reductive stripping; U(Ⅳ); Pu(Ⅳ)

2017-05-10；

2017-08-24

核电后处理重大专项

于 婷(1986—)，女，山东淄博人，博士研究生，核燃料循环与材料专业，E-mail: yuting043703@126.com *通信联系人：叶国安(1964—)，男，安徽南陵人，博士，研究员，主要从事核燃料后处理研究，E-mail: yeguoan@ciae.ac.cn

TL243

A

0253-9950(2017)06-0413-09

10.7538/hhx.2017.39.06.0413