再谈积分学——宏积分

刘春凤，袁书娟

(华北理工大学 理学院，河北 唐山 063009)



再谈积分学
——宏积分

刘春凤，袁书娟

(华北理工大学 理学院，河北 唐山 063009)

积分；宏积分；核元素

积分学包括不定积分、定积分、二重积分、三重积分、曲线积分和曲面积分。尽管不同的积分概念来自不同的实际背景，然而它们通过数学思维抽象出来的方法是类似的。因此，通过将各类积分定义的模式整合归一，给出宏积分定义、拓展及性质，以便学生领悟数学抽象思维的魅力，并进一步理解积分概念的深刻内涵。

积分是微积分学的核心，其中定积分、重积分、曲线积分和曲面积分等概念均来源于实践又应用于实践， 分析其概念的本质都是某种和式的极限，所以将各类积分定义模式进行整合归一，讨论其共同的属性在数学研究中显得尤为重要。

1 宏积分定义

定义1.1 设Rk为k维实空间(k=1,2,3)，k维区域Ωk⊂Rk，Pk为Ωk中的点，f(Pk)是定义在区域Ωk上的有界实函数，依照微元法的思想方法[，构造宏积分定义如下：

(1)

(3)求和：将n个小区域上的核元素相加，得积分和Sn

(2)

(4) 取极限：当区域Ωk的分割无限细密时，若存在实数I，使得

(3)

则称I为f(Pk)在Ωk上的k重积分，记作：

(4)

特别地：

(1)k=1的情形(直线段上的积分)

(5)

(2)k=2的情形(平面片上的积分)

(6)

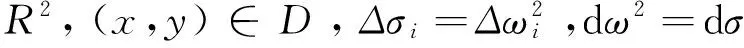
(3)k=3的情形(立体块上的积分)

(7)

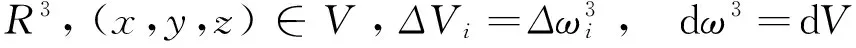
2 宏积分定义的拓展

宏积分的定义不仅能够整合重积分的概念，而且可以拓展到积分区域为平面曲线或空间曲面[2]的情形。

(1)平面曲线弧段上的积分

定义1.2设L为xoy面内的一条光滑曲线弧函数f(x,y)在L上有界。如果对于曲线L上的黎曼积分和f(ξi,ηi)Δsi总存在实数I使得Sn=I，则称I为函数f(x,y)在曲线弧L上对弧长的曲线积分或第I类曲线积分记作

∫Lf(x,y)ds

(8)

其中ΔMi=f(ξi,ηi)Δsi(i=1,2,...n)称为曲线积分的核元素，即

(9)

(2)空间曲面片上的积分

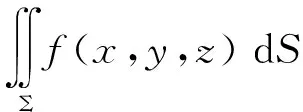
(10)

其中ΔMi=f(ξi,ηi,ζi)ΔSi(i=1,2,...n)称为曲面积分的核元素，即

(11)

(3)向量函数在平面有向曲线弧段上的积分

定义1.4L为xoy面内的一条分段光滑有向曲线弧段向量函数在L上有界。如果对于曲线L上的黎曼积分和总存在实数I使得Sn=I，则称I为函数(x,y)在有向曲线弧L上对坐标的曲线积分或第Ⅱ类曲线积分记作

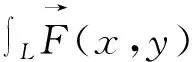
(12)

(13)

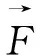
(7)向量函数在空间曲面片上的积分

(14)

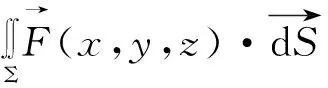
(15)

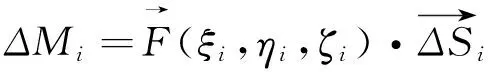
(16)

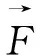
概念的抽象性是数学的特点之一。数学概念是抽象的，数学的思想方法也是抽象的(如加、减、群等)，整个数学都是抽象的。但是“抽象”不是目的，不是人为地增加理解难度，而是为了抓住事物的本质。通过抽象，把复杂变得简单、混沌变得有序，无关变得统一。

为了便于读者理解宏积分定义，我们不妨聚其躯干，略其枝节，简化定义1.1如下：

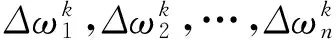
(17)

从抽象并简化以后的宏积分表达式不难看出，重积分的结果就是对核元素的积分，宏积分模型的核心就是核元素[3]的结构。

可以证明，当f(Pk)在有界闭区域Ωk上连续时，一定存在实数I，使得

(18)

具体来说：

(1)当f(x)在闭区间[a,b]⊂R上连续时，核元素dM=f(x)·dx，一定存在实数I使得

(19)

此时也称f(x)在闭区间[a,b]上可积。

(2)当f(x,y)在有界闭区域D⊂R2上连续时，核元素dM=f(x,y)·dσ，一定存在实数I使得

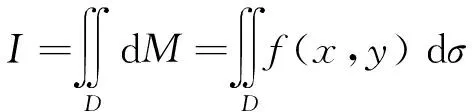
(20)

此时也称f(x,y)在闭区域D上可积。

(3)当f(x,y,z)在有界闭区域V⊂R3上连续时，核元素dM=f(x,y,z)·dV，一定存在实数I使得

(21)

此时也称f(x,y,z)在闭区域V上可积。

(4)当f(x,y)在有界闭弧段L上连续时，核元素dM=f(x,y)·ds，一定存在实数I使得

(22)

此时也称f(x,y)在有界闭弧段L上可积。

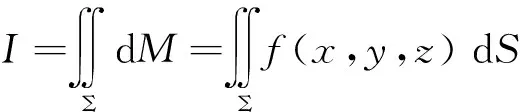
(23)

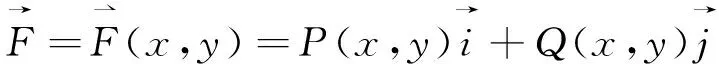
(24)

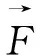
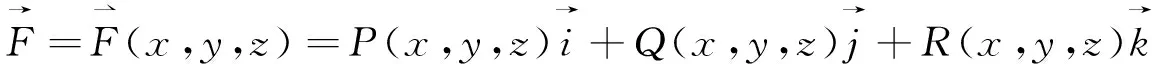
(26)

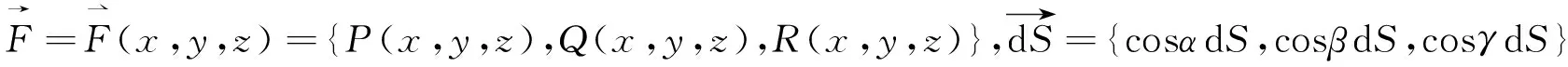
(27)

为计算方便，引入记号 dydz=cosαdS， dzdx=cosβdS，

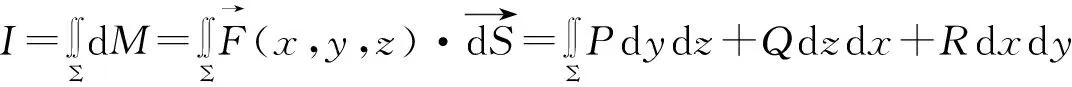
(28)

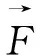
3 宏积分性质

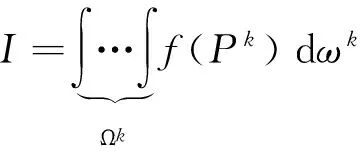
(29)

(30)

性质4.3(单位性)如果在区域Ωk上f(Pk)≡1，ωk为区域Ωk的度量，则

(31)

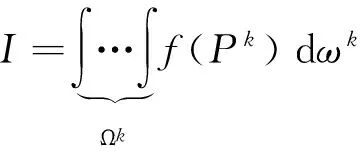
性质4.5(保序性)在区域Ωk上，f(Pk)g(Pk)，则有

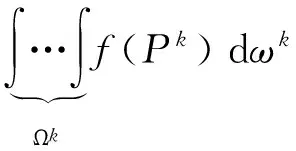
4 结论

尽管不同的积分概念来自不同的实际背景，但积分的本质属性和内在联系不会发生改变。从宏积分表达式不难看出，宏积分的结果就是对核元素的积分，宏积分模型的核心就是核元素的结构，故在以后积分应用问题的处理中关键是寻求核元素。

[1] 刘春凤. 高等数学上[M]. 北京：科学出版社，2007.

[2] 同济大学应用数学系. 高等数学(第六版)[M]. 北京：高等教育出版社,2004.

[3] 袁书娟，杨爱民. 独立学院大学数学"五环"教学模式的研究与实践[J].广西教育，2013.

Further on Integral Calculus:Macro Integral

LIU Chun-feng, YUAN Shu-juan

(College of Science, North China University of Science and Technology, Tangshan Hebei 063009, China)

integral; macro integral; nuclear element

Integral calculus includes indefinite integral, definite integral, double integral and triple integral, curve integral and surface integral. Although different integral concept from different actual background, however, their mathematical thinking of abstracting method is similar. Therefore, through the integration of all kinds of integral definition mode into one, macro integral definition, development and nature are given, so that students can understand the charm of mathematics abstract thinking, and to further understand the profound connotation of the concept of integral.

2095-2716(2017)01-0108-06

O172.2

A