基于惯性参数的动力总成悬置系统解耦分析

周宇杰，雷 刚，贺艳辉，张骑虎

（重庆理工大学 汽车零部件制造及检测技术教育部重点实验室，重庆 400054）

基于惯性参数的动力总成悬置系统解耦分析

周宇杰，雷 刚，贺艳辉，张骑虎

（重庆理工大学 汽车零部件制造及检测技术教育部重点实验室，重庆 400054）

基于传统的动力总成悬置系统6自由度模型，可得到与6自由度相关的解耦率。而通过商业软件Adams建立动力总成悬置系统模型并利用vibration插件进行计算时，平动方向上的解耦率与传统6自由度模型相同，而转动方向上的三个分量被分解为6个与惯性参数相关的分量。基于Adams模态能量表达，用Matlab软件编写动力总成悬置系统的解耦率计算程序，利用多目标优化方法对悬置系统进行优化设计。结果表明，对悬置刚度进行优化能有效提高解耦率。

振动与波；振动解耦；多目标优化；悬置系统

汽车动力总成悬置系统是汽车振动系统中一个重要的子系统,该系统性能的优劣直接影响整车NVH性能。因此设计有效的悬置系统，减弱由动力总成引起的振动和噪声，显得尤为重要。一个有效的悬置系统，首先要控制各固有频率在合理的范围内，同时尽可能解除多自由度的振动耦合[1]。一般系统解耦有两种方法：刚度矩阵解耦和能量解耦。能量解耦作为一种有效的振动解耦方法已被广泛用于动力总成悬置的设计和优化中。文献[2]提出能量解耦法，通过解除发动机悬置系统的振动耦合，对悬置系统进行优化设计；文献[3]推广了能量解耦法的应用范围，实现了系统主振型的解耦以及多目标优化。

目前能量解耦主要以传统6自由度模型分析为主，得到与自由度对应的解耦率。本文主要研究基于惯性参数的能量解耦方法，得到与惯性参数对应的解耦率。

1 动力总成悬置的模态计算

1.1 动力总成悬置系统数学模型的建立

在悬置系统解耦设计时，运用弹性支撑空间刚体动力学理论构造方程。动力总成的固有频率远大于悬置系统的频率，因此把发动机、离合器和变速器等组成的动力总成作为空间弹性支承刚体。橡胶悬置元件简化成三向线性弹簧。建立动力总成坐标系见图1，原点O在动力总成质心处，X轴与汽车前进方向相反，Z轴垂直于气缸上端面指向上方，Y轴按右手定则确定。

图1 动力总成坐标系

在分析动力总成的固有特性即低频范围内的刚体振动时，忽略悬置元件的阻尼，即将系统简化为6自由度无阻尼自由振动系统，系统的振动微分方程为

其中M为动力总成悬置系统质量矩阵

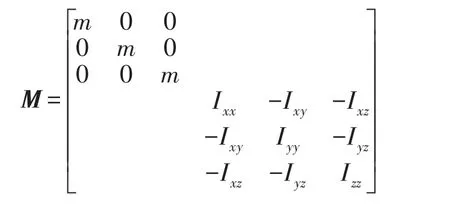
K为系统刚度矩阵

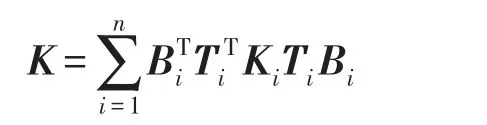
Ki为第i个悬置的三个方向的刚度矩阵

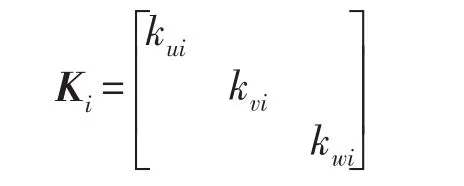
Bi为第i个悬置的位移矩阵

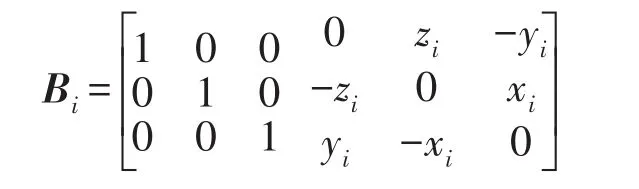
Ti为第i个悬置的局部坐标系o-u-v-w坐标轴相对于发动机质心坐标系O-X-Y-Z坐标轴的方向角所组成的方向余弦矩阵

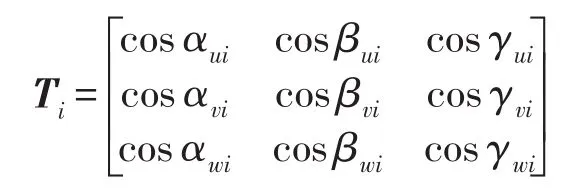
建立动力学方程后，解微分方程可获得固有频率、振型等，即可分析系统的模态特性。对于6自由度动力总成悬置系统则有6个固有频率和对应频率下的振型。

1.2 动力总成悬置系统能量解耦

能量解耦是从能量的角度来进行解耦，系统按坐标轴方向进行解耦。当作用在某坐标轴方向上的激振力所做的功全部转化成系统在该方向的能量时，则认为系统在该方向上解耦。即沿着某坐标轴方向的激励只引起该方向的振动。

对于悬置系统，不考虑阻尼能量耗散，假设机械能守恒。每1阶主振动的动能和势能之和是保持不变的。任意1阶主振动的总能量用最大动能或最大势能来表示。

第i阶主振动的总能量为

将上式展开可得平动能量和转动能量。

平动能量分量可由下式表示

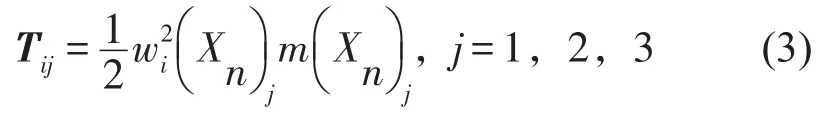
转动能量分量可由下式表示

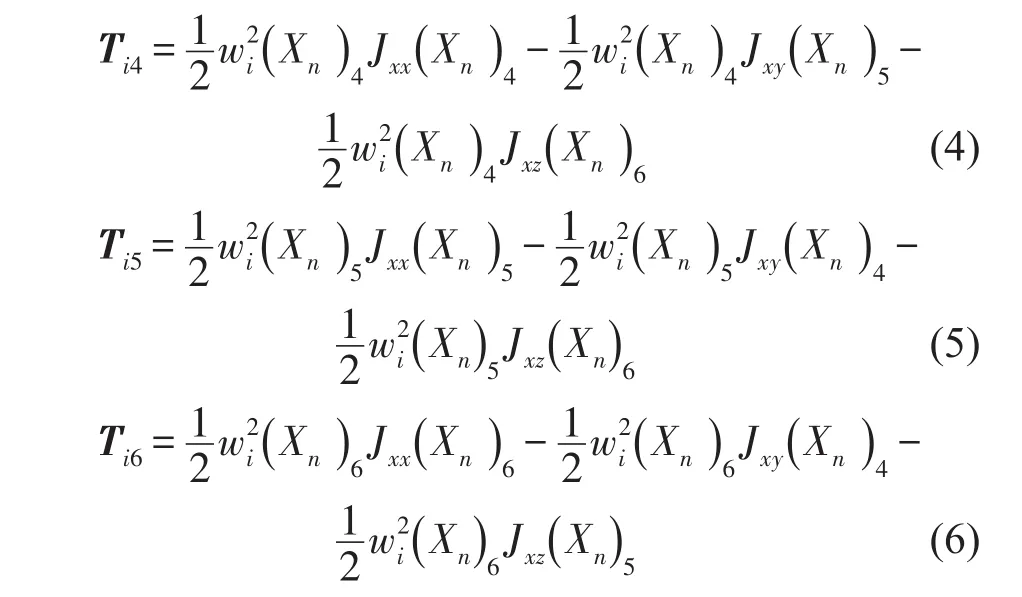
当系统以第i阶固有频率振动时，第k个广义坐标上能量分布矩阵可表示为

其中Xi表示第i阶的振型向量；Mkl表示系统质量矩阵的第k行的第l列元素；wi表示第i阶的固有频率。

第k个广义坐标上分配到的动能所占系统总动能的百分比为

其中Tpk的大小表示能量集中程度。如果Tpk值为100%，表明在某阶频率下，主振动的能量全部集中在第k个坐标方向，与其他方向独立。通常情况下，一个系统的能量解耦程度是根据解耦率来判断的，解耦率越大表示该系统能量解耦程度越好，各阶模态的解耦率达到100%是系统解耦的理想状态。但是在实际工程应用中，由于各种不可避免的因素，动力总成悬置系统的各阶模态解耦率达到85%时，则认为该系统解耦良好。

2 Adams中的模态能量表达

在Adams中进行模态能量计算时，首先将系统分成若干子系统，分别计算各个子系统的能量，再求和得到总能量。其中任意子系统的模态能量又包括9个分量[4]。在动力总成悬置模型中，可将整个模型当作一个系统。即整个系统模态能量就是动力总成的模态能量。假设φi为第i阶主振型向量。考虑动力总成质量的影响，对应沿广义x、y和z方向的平动能量

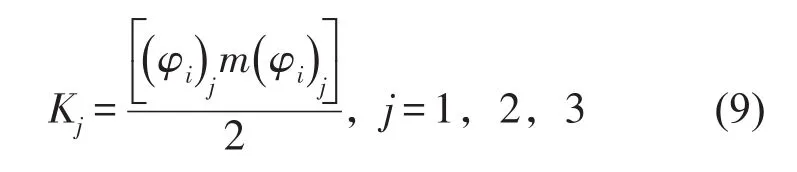
动力总成转动惯量的影响可由下式表示

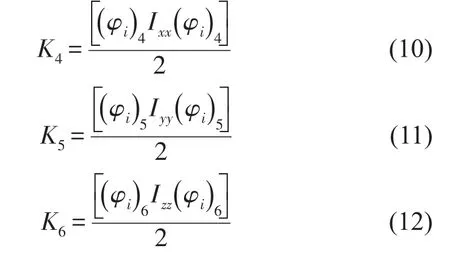
动力总成惯性积的影响可由下式表示

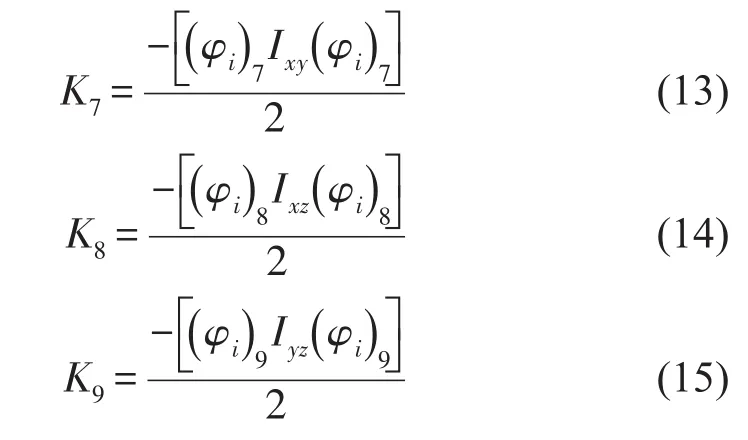
第e个能量分量在该阶主振动总能量中的百分比为

动力总成悬置系统6自由度模型有6阶主振型，可得到一个6×9模态能量分布矩阵，可称为基于惯性参数的能量分布矩阵。

3 两种模态能量的比较

利用Matlab软件，建立悬置系统的振动方程[5]。基于传统6自由度模型理论和第2节中公式编写两套解耦率计算程序分别得到基于传统6自由度理论的解耦率和基于惯性参数的解耦率。在Adams建模时，先进行适当简化。动力总成可视为形状简单的刚体，悬置元件可简化成三向线性弹簧[6]。建模后利用vibration插件进行模态计算，得到6阶固有频率及解耦率。以上三种计算方法得到的解耦率如表1所示。从表1可以看出，三种解耦率在X、Y、Z方向上大致相同，而在RXX、RZZ方向上解耦率明显存在差异。

通过分析两种模态能量表达式可知，Adams软件在定义解耦能量时，平动能量与传统的六自由度模型的解耦方式相同，而转动能量则拆分成6个分量。基于传统的6自由度模型得到的解耦率与6个自由度对应，物理意义明确。而基于Adams计算的解耦率不与系统的六自由度对应，分别描述动力总成平动质量、转动惯量和惯性积对系统主振动能量的影响，直接反映出各惯性参数对系统解耦率的影响。

4 算例及优化分析

4.1 动力总成悬置系统参数

发动机动力总成悬置系统计算和优化所需的参数可以通过测试和计算获得。表2为动力总成系统的质量及转动惯量参数，由试验测得。表3为悬置点相对质心位置坐标，通过数模读取。表4为各悬置元件的主轴刚度，由试验测定。

4.2 动力总成悬置系统优化分析

在进行优化时，优化目标为6个方向上的解耦率达到最大值。根据动力源的激励特性，本例优化时主要考虑垂直方向z向和绕曲轴旋转RXX向的解耦率。从表4中可知，按传统六自由度理论计算解耦率，RXX向的解耦率为79.44%，z向的解耦率仅有72.39%，均未达到85%以上。故有必要对原悬置系统的解耦率进行优化。

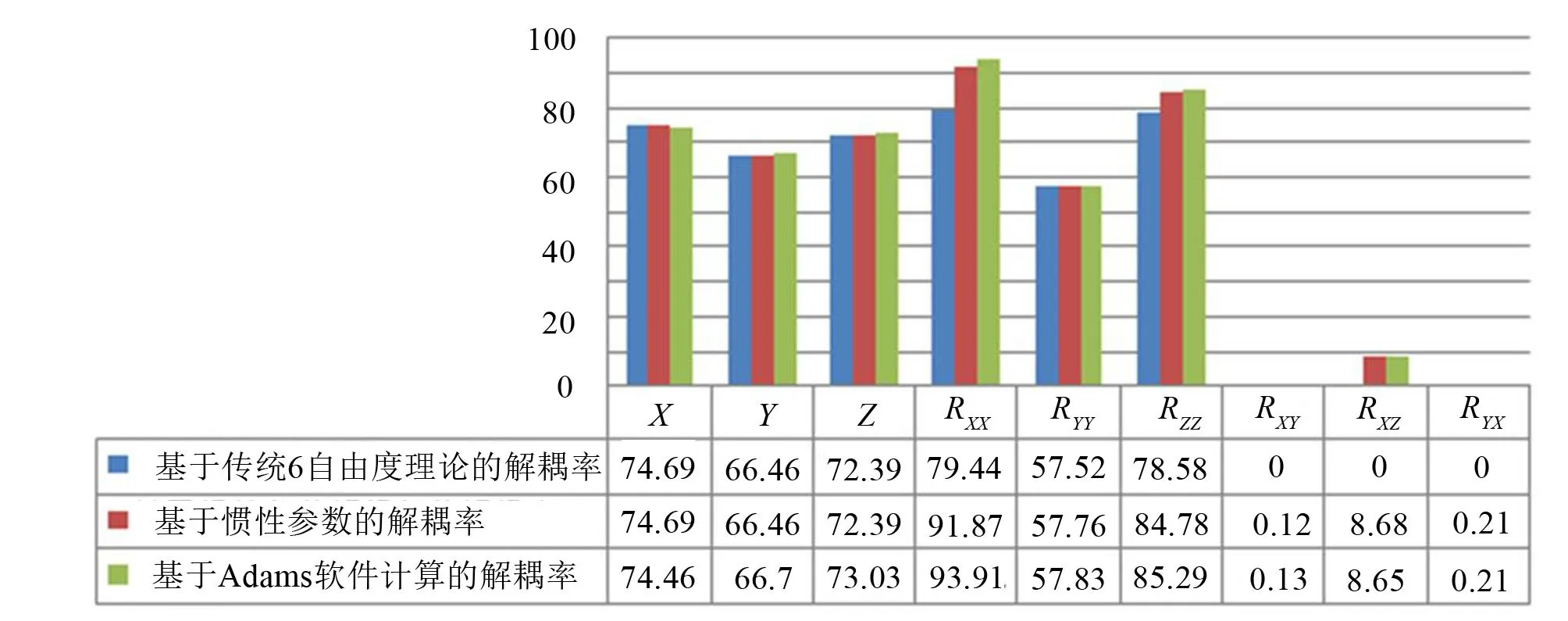
表1 三种不同方式解耦率的比较

表2 动力总成质量与惯量参数

表3 悬置弹性中心坐标/mm

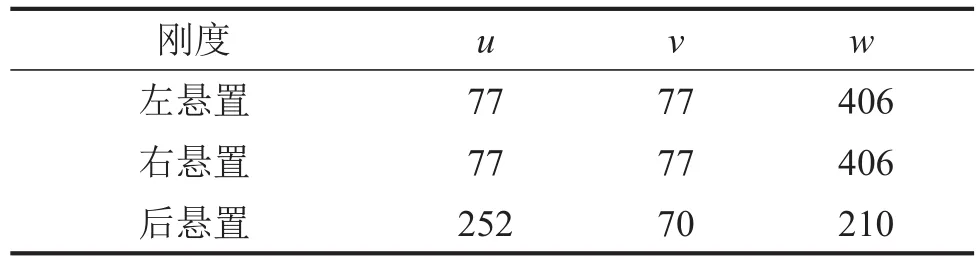
表4 悬置元件刚度/(N·mm-1)

本例选用Matlab优化工具箱中的fgoalattain函数对其进行优化设计。由于fgoalattain函数在进行求解时，目标函数为最小值。而本例优化目标函数是解耦率最大，因此在优化前应先将本例优化目标函数进行转换。

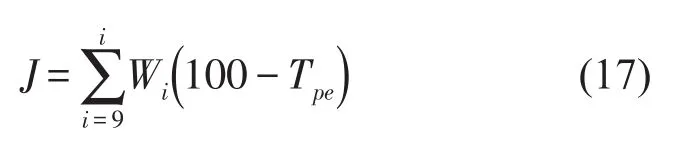
在实际工程中，动力总成的质量、质心、转动惯量和惯性积参数均已确定，故优化时不作为优化变量。受到动力总成安装位置的限制，设计变量只选取各个悬置件的刚度而不考虑悬置元件的坐标。以各悬置的3个主轴刚度作为优化变量[7]。悬置系统刚度过大不利于系统的减振性能，而悬置系统刚度过小又不利于悬置对动力总成的支承。综合考虑，把这9个刚度的取值范围限制在30 N/mm至300 N/mm。对于纵置发动机来说，主要考虑模态在Z方向和在Rxx方向的解耦率，故这两阶振型上的加权因子要比其他阶高。通过调整加权系数使计算结果收敛。最终确定加权系数如表5所示。

表5 六个自由度上加权系数

用Matlab编写多目标优化程序，输入相关约束参数、加权系数。计算后可获得针对9个变量的解耦率优化结果，如表6所示。在z向和RXX向的解耦率有较大的提高，整体解耦率也有所改善。综上所述，通过对动力总成3个悬置元件各主轴刚度的调整，达到了对悬置系统6个自由度解耦率优化的目的，完成了动力总成悬置系统的初步优化。

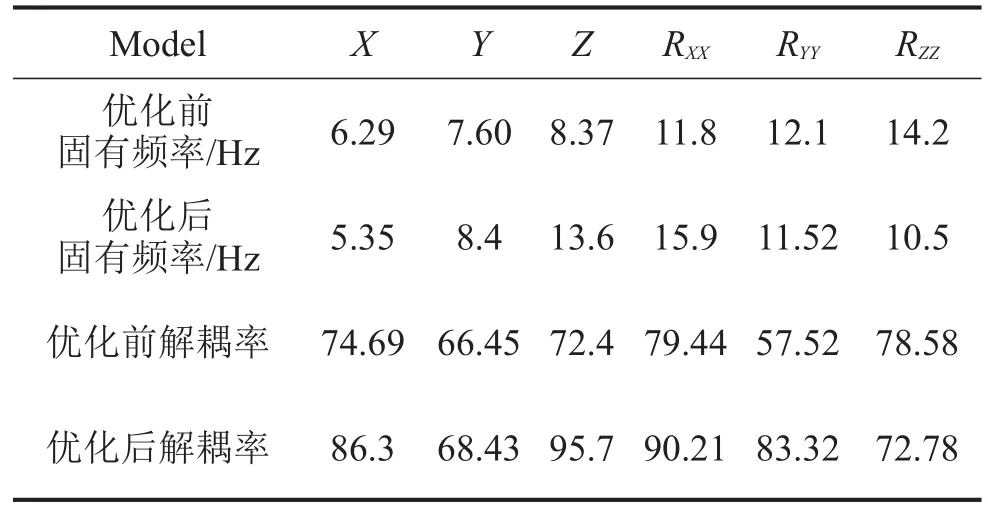
表6 优化后结果对比

5 结语

动力总成悬置系统解耦率的两种表达形式分别考虑了振动能量在系统自由度方向上的解耦和惯性参数对解耦的影响。通过对动力总成悬置系统进行动力学建模，研究了两种能量解耦的特性。利用Matlab优化工具，在解耦理论基础上对动力总成悬置主轴刚度进行了优化设计。结果表明，刚度值优化后提高了动力总成的主振动解耦率，改善了系统的振动特性。

[1]沈志宏，郭福祥，方德广，等.基于能量解耦法的动力总成悬置系统优化设计[J].噪声与振动控制，2010，30(3)：35-37.

[2]徐石安.汽车发动机弹性支撑隔振的解耦方法[J].汽车工程，1995，17(4)：198-204.

[3]攀兴华，陈金玉，黄席樾，等.发动机悬置系统多目标优化设计[J].重庆大学学报（自然科学版），2001，24(2)：41-44.

[4]童炜，侯之超.关于动力总成悬置系统模态能量表达的一个注记[J].汽车工程，2013，35(3)：32-36.

[5]黄鼎友，许荣明.基于Matlab的发动机悬置系统设计及优化[J].噪声与振动控制，2007，27(1)：65-68.

[6]李令兵，陈剑，吴赵生.基于Adams的发动机悬置系统设计[J].噪声与振动控制，2007，27(6)：54-56+70.

[7]史文库，洪哲浩，赵涛.汽车动力总成悬置系统多目标优化设计及软件开发[J].吉林大学学报(工学版)，2006(5)：654-658.

DecouplingAnalysis of Powertrain Mount Systems Based on Inertial Parameters

ZHOU Yu-jie,LEI Gang,HE Yan-hui,ZHANG Qi-hu
(Key Laboratory of Manufacture and Test Techniques for Automobile Parts,Chongqing University of Technology,Chongqing 400054,China）

The decoupling rate associated with 6 DOFs is obtained based on the traditional 6-DOF model of powertrain mounting systems.The model of the powertrain suspension system is built by means of commercial software Adams,and the plug-in vibration code is used for calculation.In the calculation,the decoupling rate in the translation direction is the same as that of the traditional 6-DOF model,but the three components in the rotational direction is divided into 6 components which are related to the inertial parameters.Based on the expression of Adams modal energy,the Matlab software is used to write the program for decoupling rate computation of the powertrain mounting system.Finally,the optimization design of the mount system is carried out by using the multi-objective optimization method.The results show that the optimization of the mount stiffness can effectively raise the decoupling rate.

vibration and wave;vibration decoupling;multi-objective optimization;mount system

U260.331+.5

A

10.3969/j.issn.1006-1355.2017.06.019

1006-1355(2017)06-0094-04

2017-04-19

周宇杰（1992-），男，湖北省襄阳市人，硕士研究生，目前从事汽车CAE和NVH方向研究。

雷刚（1967-），男，博士，教授，研究方向为计算力学、CAD、CAE。E-mail:ganglei4786@126.com