基于GA-OCPA学习系统的无人机路径规划方法

刘鑫，杨霄鹏，刘雨帆，姚昆

1. 空军工程大学 信息与导航学院，西安 710077 2. 北京航空航天大学 电子信息工程学院，北京 100083

基于GA-OCPA学习系统的无人机路径规划方法

刘鑫1，*，杨霄鹏1，刘雨帆2，姚昆1

1. 空军工程大学 信息与导航学院，西安 710077 2. 北京航空航天大学 电子信息工程学院，北京 100083

为解决未知空域中无人机路径规划方法实时性和适用性不足的问题，以生物应激条件反射理论为基础，将无人机实时路径规划类比为在外界条件刺激下的一种自学习行为。首先，将概率自动机与遗传算法相结合，设计了基于Skinner操作条件反射理论框架(GA-OCPA)的学习系统；然后，将无人机规避机动的飞行速度、滚转加速度和拉升加速度作为系统学习的行为，并计算每次学习尝试之后的选择概率和个体适应度，通过遗传算法搜索最优行为进而得到最优路径；最后，运用增量多层判别回归树(IHDR)对学习得到的最优行为建立知识库，形成威胁状态与路径规划的匹配映射。实验结果表明GA-OCPA学习系统对于无人机路径规划具备有效性和适用性。

无人机；路径规划；遗传算法；操作条件反射；概率自动机

路径规划的常规模式是通过传感器感知周围环境信息，进而完成实时路径规划。传统方法主要有：拓扑法、栅格法、动态规划法、势场法、最优控制法等[1-7]。这些方法存在迭代次数多、计算复杂度高、实时性不足等缺点，无法良好地适用于无人机技术高速发展背景下空域中多种威胁因素并存时的路径规划需求。

无人机的动力学模型复杂程度高，同时所面向的空域环境也具有高度不确定性[8]。因此，在面临威胁时完全依靠飞控计算机进行编程实现路径规划会使无人机的规避机动滞后，极大地制约了无人机性能的发挥[9]。考虑到无人机面临空中威胁的突发性且具有相对运动速度大的特点，通过模仿生物体的学习活动，使无人机在其性能约束的条件下具备自主学习能力，可以大大提高威胁出现时路径规划的实时性、准确性和适用性。这种基于自学习的人工智能方法已经在无人机和机器人控制领域得到了广泛应用。文献[10]将博弈学习理论应用于多无人机汇聚问题，各个无人机智能体之间通过学习算法得到任务要求的路径规划结果。文献[11-12]分别提出了几何协作学习算法和几何强化学习算法，提高了单机和多机协同下的路径规划能力。文献[13]提出了基于Q学习的机器人和无人机路径规划算法，通过智能体与环境的信息交互实现了在线学习。文献[14]基于证据推理理论对无人机水面舰艇的碰撞风险进行评估，并通过学习得到最优互惠避撞策略，可借鉴到无人机应对空中威胁的路径规划方法中。

强化学习算法虽然具有较好的实时性，其对于机器人可以实现简单的控制需求，而无人机的任务复杂程度更高，单一强化学习方法不能保证适用性。因此，针对未知空域中的无人机路径规划问题，本文以Skinner操作条件反射理论(Operant Conditioning, OC)[15]为框架，结合遗传算法(Genetic Algorithm, GA)，在概率自动机(Probabilistic Automata, PA)的平台基础上设计了基于遗传算法的操作条件概率自动机(Genetic Algorithm-Operant Conditioning Probabilistic Automata, GA-OCPA)学习系统。通过学习系统对路径规划中无人机的飞行速度、滚转加速度和拉升加速度进行学习，根据这3个参数的变化建立无人机动态避撞区模型。再运用操作条件反射机制学习最优行为并与环境进行交互获得反馈信息，进而完成信息熵值的更新，同时采用增量多层判别回归树(Incremental Hierarchical Discriminant Reqression, IHDR)方法对最优状态下的行为建立知识库[16-17]。最后，通过仿真验证了所提方法的适用性、必要性、有效性及其优势。

1 GA-OCPA学习系统设计

仿生学是根据生物体在特定条件下的行为与环境交互后得到的反馈符合个体的取向性，则在相似条件下生物体完成类似行为的概率会增大。因为无人机采取避撞机动时的飞行速度、滚转加速度和拉升加速度均为可控参数，所以可通过建立仿生学习系统对采集到的行为信息进行学习。

将遗传算法(GA)思想与概率自动机(PA)相结合设计GA-OCPA仿生学习系统的结构如图1所示。

其中每个个体代表无人机采取避撞机动行为方式的一个集合，通过作用于环境获得的反馈实现状态更新和性能评价，采用Skinner OC理论对个体的最优行为方式进行学习，并计算信息熵值作用于GA对个体行为方式的集合进行寻优，进而使无人机适应环境中的威胁。

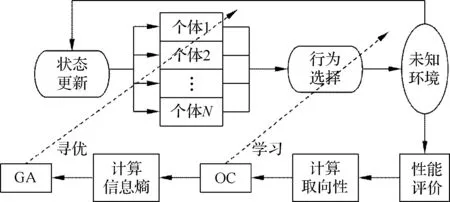
图1 GA-OCPA学习系统结构图Fig.1 Structure diagram of GA-OCPA learning system

1.1 学习系统数学定义

根据PA的定义形式，GA-OCPA系统的数学定义为

GA-OCPA=(x,N,Q,o,F,φ,S,H,G)

(1)

该九元组的各部分含义为:

1)x=x(t)为系统的内部状态，是实际控制系统的状态值。

2)N={ni|i=1,2,…,m}为对系统内部状态x=x(t)进行离散化之后的结果，是系统内部所有离散化状态组成的集合，且m为离散化个数，ni∈N为第i个离散的状态。

3)Q={Aj|j=1,2,…,M}为系统的种群，其中每个种群包含N个个体，Aj∈Q为第j个个体，且个体Aj={ajk|k=1,2,…,r}即学习系统行为方式的集合，ajk为个体Aj中的第k个行为方式，个体A对其包含的r个行为方式进行编码。

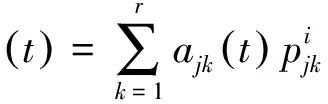
(2)

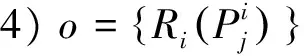
5)F:ni(t)×ajk(t)→ni(t+1)为状态转移，F是由无人机采取机动行为引起的状态变化ni(t)→ni(t+1),且状态ni(t+1)只与前一时刻状态ni(t)和该时刻行为ajk(t)有关。

6)φ={φ1,φ2,…,φm}为系统的取向函数，状态ni(t)的取向值可以用φi表示。当某一状态的取向值φ→0时，表示对该状态的取向程度高且学习性能好；当某一状态的取向值φ→1时，表示对该状态的取向程度低且学习性能差。因此，系统的概率矢量Pj通过φi(t)的变化趋势进行更新。

7)S:oj(t)→oj(t+1)为Skinner OC学习算法，通过算法完成对最优行为方式的选取。

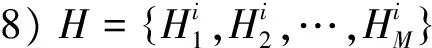
(3)

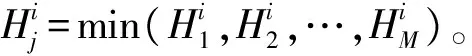
9)G:ni(t)→Aj表示系统通过遗传算法的进化思想获得最优个体Aj。

1.2 Skinner OC算法设计

因为与系统进行交互的位置环境的状态是动态的，所以引入奖励概率作为行为的评价信号，系统状态ni(t)获得奖励的概率为

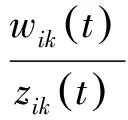
(4)

式中：wik(t)为行为ajk获得累计奖励的总和；zik(t)为系统状态为ni(t)时，行为ajk被选择的次数。

当a(t)=ajk时，有

(5)

zik(t+1)=zik(t)+1

(6)

(7)

当a(t)=ajk1且k≠k1时，有

wik(t+1)=wik(t)

(8)

zik(t+1)=zik(t)

(9)

dik(t+1)=dik(t)

(10)

算法通过对前后两时刻之间的取向值之差对行为概率p(t)进行更新。

当φi(t+1)-φi(t)<0时，有

(11)

(12)

其中

(13)

(14)

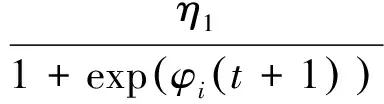
(15)

当φi(t+1)-φi(t)>0时，有

(16)

(17)

其中

(18)

(19)

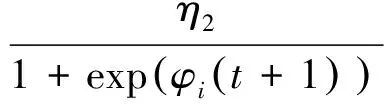
(20)

式(11)～式(20)中:α(t)和β(t)为算法的学习速率，且0<α(t)<1,0<β(t)<1；η1和η2均为大于0的常数；Δ为行为概率的增量部分。

将取向值函数φi(t)加入行为选择概率公式能够改变系统学习速度，同时使学习系统更好地表现出生物体的取向性特点。当任意状态取向值增大时，其行为选择概率更新的增量值就会随α(t)的减小而减小，进而使学习速度降低；同理，当状态取向值减小时会使系统学习速度加快。且行为选择概率更新使得第j个个体的行为熵更新为

(21)

1.3 算法学习流程

无人机基于GA-OCPA学习系统的路径规划流程可以分为6个步骤：

步骤1建立避撞区模型

由于无人机在空间中遭遇碰撞威胁多数采用向右滚转并拉升、向左滚转并拉升或拉升的机动方式，且无人机避撞机动时的飞行速度、滚转加速度和拉升加速度均对避撞区的形状和大小造成影响，故通过对参数的学习以增强无人机应对威胁的避撞能力是十分必要的。

因此，通过分析无人机与威胁的空间几何关系，根据相对飞行状态信息和无人机采取的规避机动措施建立三维动态避撞区模型。

步骤2学习系统初始化

初始阶段将学习系统的迭代次数t设置为0，根据无人机本身具备的路径规划能力随机获取r个初始数据组成个体Aj={ajk|k=1,2,…,r}。

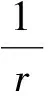
步骤3遗传算法对个体进行训练

将pjk(0)=1/r代入式(3)求得系统的初始信息熵，即此时个体Aj的适应度值。基于遗传算法的进化思想在N个个体组成的种群中选取最优个体作为Skinner OC算法的行为方式集合。

步骤4基于Skinner OC算法选择最优行为

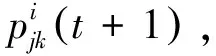
步骤5判定是否结束一次实验

设定无人机的最小安全间隔R0,计算比较无人机实施以上行为之后形成的避撞区与威胁之间的距离是否大于R0。若大于，则进入步骤6；否则，跳转至步骤2。

步骤6运用IHDR对适用的路径规划方法进行知识存储，实现“威胁-行为”的映射。存储具体方法参见文献[17]。

2 无人机三维动态避撞区建模

2.1 空间几何关系

本文采用最接近点(Closest Point of Approach, CPA)的几何算法，计算无人机与威胁之间最接近点的距离[18]，将最接近点距离与无人机规定的最小安全间隔相比较，从而判定无人机与威胁是否存在碰撞的可能。

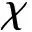
无人机A的速度矢量可以表示为

VA=VAxx+VAyy+VAzz

(22)

又由几何关系可得

(23)

故

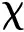
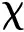
(24)

同理

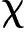
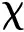
(25)

其中：x,y,z分别为x,y,z方向上的单位矢量。无人机与威胁速度矢量夹角的余弦值为

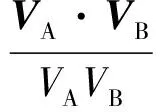
(26)

根据几何关系可得

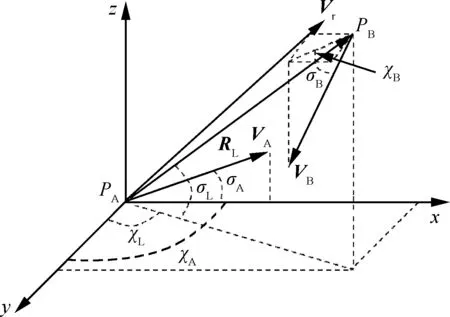
图2 无人机与威胁的几何关系Fig.2 Geometric relationship between UAV and threat

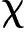
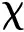
sinσAsinσB)

(27)

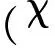
sinσAsinσB)

(28)

故

cos(∠VA,VB)=sinσAsinσB+

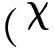
(29)

威胁与无人机的相对速度为

Vr=VB-VA

(30)

且相对速度大小为

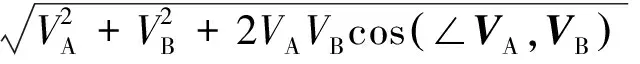
(31)

又因为

(32)

故相对速度与坐标系的夹角为

(33)

(34)

2.2 紧急避撞区模型

模型建立的基础是认为无人机通过广播式自动相关监视技术(Automatic Dependent Surveillance-Broadcast, ADS-B)和第二代空中交通警戒与防撞系统(Traffic Alert and Collision Avoidance System Ⅱ,TCAS Ⅱ)等监视技术[19]能够准确获得威胁的位置和速度等状态信息。无人机在三维空间遭遇威胁，为了避免碰撞通常采用水平方向滚转机动、垂直机动或两者相结合的机动措施[20]。因此，根据无人机的避撞机动方式将避撞区域分为向右滚转并拉升、向左滚转并拉升和拉升3种类型。

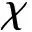
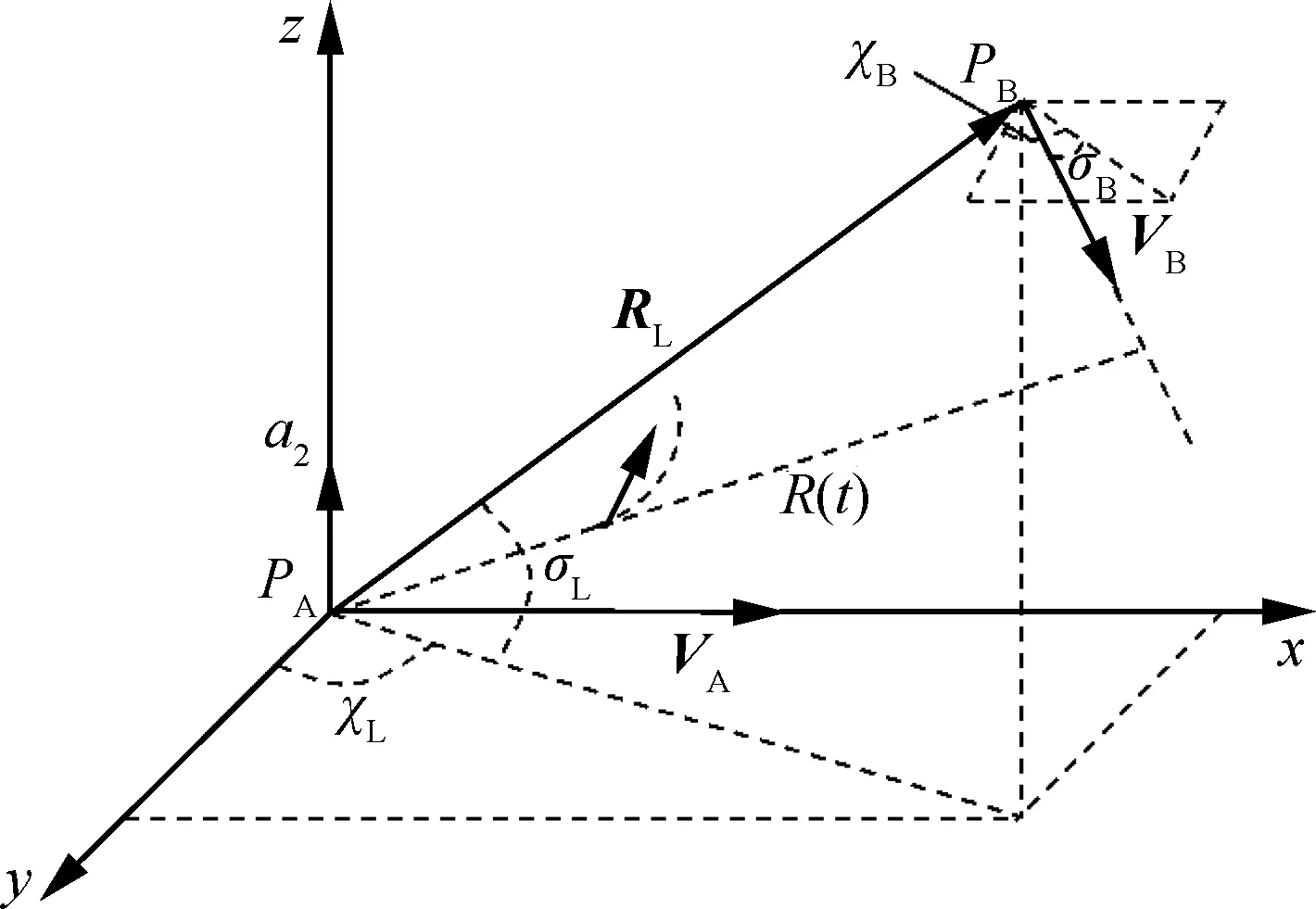
图3 向上拉升机动的几何关系Fig.3 Geometric relationship of climbing maneuver

经过t时间后，当无人机与威胁之间的最近距离恰好为最小安全间隔R0时达到避撞区的临界情况，初始位置为避撞区的边界值，忽略飞行过程中可能存在的侧滑角等误差影响，可以得到t时刻无人机与威胁之间的距离R(t)为

(35)

根据无人机与威胁达到最近距离时恰好等于最小安全间隔R0,可以建立二元方程组：

{R′(t)=0

R(t)=R0

(36)

由于对R(t)求导可简化为对R2(t)求导，整理可得：

(37)

同理，当同时进行水平方向上最大程度右滚转和垂直方向上最大程度向上拉升机动时，即产生一个y轴上的大小为a1的加速度和一个z轴上的大小为a2的加速度，得到：

(38)

根据式(36)，由R2(t)求导代替对R(t)求导，整理得：

(39)

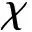
同理，当同时进行水平方向上最大程度左滚转和垂直方向上最大程度拉升机动时，令a1<0即可得到数学模型方程，此处不做赘述。

三维避撞区的模型方程为二元非线性方程组，因此，可以采取迭代法进行求解，用逐次逼近的方法得到未知量t和RL的数值解。根据无人机避撞的物理过程，将t<0的部分舍弃，令此时的紧急避撞区的边界值为RL=R0。

2.3 影响因素分析

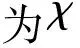
由式(37)和式(39)得到3种条件下避撞区的边界，当威胁进入3种避撞区的交集时，无人机采取任何机动都无法避免碰撞。因此无人机要在避撞区交集以外的区域采取拉升、向右滚转并拉升或向左滚转并拉升的机动完成实时路径规划。

图4 紧急避撞区模型Fig.4 Model for emergency collision avoidance area

2.3.1 无人机飞行速度对避撞区的影响

当无人机飞行速度VA=80 m/s,其他条件不发生改变时，紧急避撞区如图5所示。通过对比可见，改变无人机的速度，威胁与无人机的相对速度就会改变，因此对紧急避撞区而言，随着相对速度的变化，无人机与威胁之间接近的速度更快，在x轴上表现最明显，将使其区域范围增大；相反，会使其区域范围减小，威胁的速度改变原理相同。

2.3.2 无人机拉升加速度对避撞区的影响

当无人机的拉升加速度g=20 m/s2,其他条件不发生改变时，紧急避撞区如图6所示。

通过对比可见，对紧急避撞区而言，增大拉升加速度，无人机的机动性得到增强，缩短了与威胁之间的避撞时间，在z轴上表现最明显，将使其区域范围减小； 相反， 会使其区域范围增大，滚转加速度的改变原理相同。

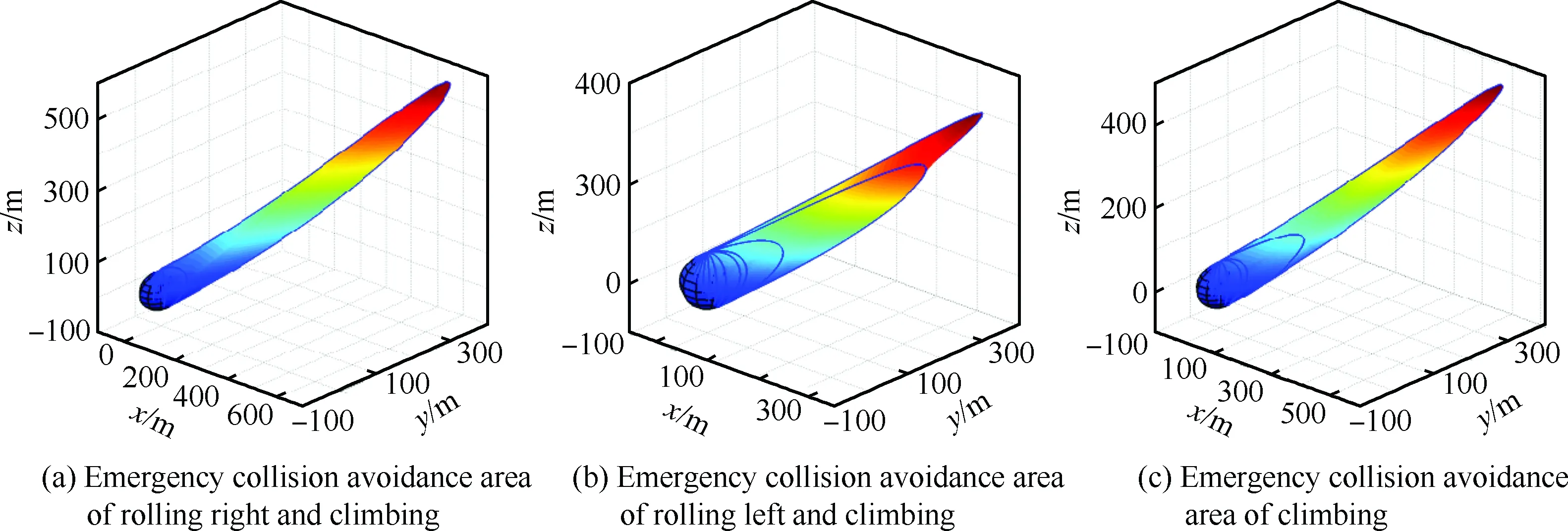
图5 飞行速度对紧急避撞区的影响Fig.5 Effect of flight speed on emergency collision avoidance area

图6 拉升加速度对紧急避撞区的影响Fig.6 Effect of climbing acceleration on emergency collision avoidance area

通过实验仿真可以看出，无人机速度、威胁速度、滚转加速度和拉升加速度是所构建避撞区的主要影响因素。分析避撞的物理过程，当增大无人机或威胁的速度时，导致相对速度增大，互相接近的速度加快，为了达到避撞的目的，碰撞区会相应增大；当无人机滚转加速度或拉升加速度增大时，无人机的机动性得到增强，缩短避撞时间，碰撞区也会相应减小，得到的仿真结果和分析结果一致。无人机的飞行速度、滚转加速度和拉升加速度都是可控因素，故利用GA-OCPA学习系统进行路径规划时，可以将对无人机速度、滚转加速度和拉升加速度的控制考虑在内。

3 仿真实验

为了验证本文所提基于GA-OCPA学习系统路径规划方法的适用性、必要性、有效性及其优势，首先对未经过学习的无人机在简单地形威胁场景下的路径规划进行了实验，然后通过实验对系统的学习效果进行了分析，最后分别对经过学习后无人机的路径规划能力在地形威胁、单一动态威胁、连续动态威胁和多种类型威胁场景下进行了仿真验证。

当无人机未经过学习时，其应对威胁时的路径规划能力较弱，仿真结果如图7所示。在简单地形威胁条件下无法有效规避威胁，故通过学习系统提高无人机规避威胁能力具有必要性。

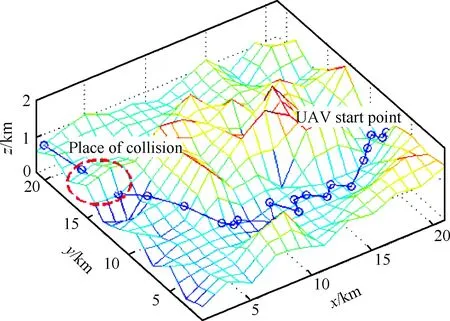
图7 未进行学习的路径规划图Fig.7 Path planning without learning

3.1 系统性能分析

本文对所提GA-OCPA学习系统与文献[12-13]提出的几何强化学习(Geometric Reinforcement Learning,GRL)算法和Q-学习算法进行了性能比较，3种学习算法均进行100次迭代，种群中包含个体数量N=50,且个体内包含行为方式个数r=10,初始概率pjk(0)=0.1。图8为适应度和概率值变化曲线，在学习进化的过程中最大适应度对应最小熵值，最小适应度对应最大熵值。

当个体被多次选择时，其包含的行为方式被选取的概率也会增加。3种学习算法对最优行为的选择概率无限趋近于1，故包含该型的个体熵值趋近于0，此时个体具有最大适应度值。由图8(a)可知，GA-OCPA系统的收敛速度最快且适应度值最早趋近于稳定。

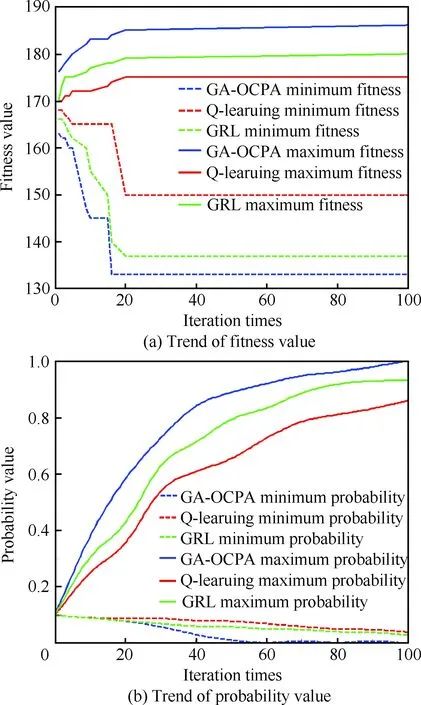
图8 适应度和概率变化趋势曲线Fig.8 Curve of changes in fitness and probability

在学习的过程中某些行为方式被选择的概率逐渐增加到0.9左右时趋于平缓且最终趋近于1。由图8(b)可以看出，GA-OCPA学习系统在3种算法中的概率值学习曲线变化率最大，说明该系统在学习中经验积累的速度最快，最早由初始阶段的随机性学习方式变为确定性学习，进而得到最优的行为方式，并通过IHDR对最优行为进行知识存储，形成威胁到路径规划映射的知识库。

实验表明GA-OCPA学习系统在动态变化的学习过程中可以较快地积累学习经验和更新行为方式，更早地由初始随机搜索阶段进入最优行为学习，具有良好的适应性，更有利于空中环境复杂的无人机路径规划。

3.2 地形威胁场景

无人机经过GA-OCPA学习系统的学习已具备一定的路径规划能力，采用地形威胁场景对无人机应对静态威胁的路径规划能力进行验证，场景仿真结果如图9所示。

本机以30 m/s的速度在第0 s启动，在进入山峰的避撞区范围时，通过先前学习经验从知识库中得出最优路径规划策略，同时对每次规划行为进行学习更新，根据不同地形的避撞区范围，无人机完成规避机动的飞行速度、滚转加速度和拉升加速度趋向最优。

图9 地形威胁路径规划图Fig.9 Path planning in terrain threat

3.3 动态威胁场景

针对无人机在现实环境中动静态威胁类型并存时的路径规划能力[21]，在地形威胁基础上分别对单一动态威胁和连续动态威胁场景进行验证。

单一动态威胁场景仿真结果如图10所示。

与地形威胁场景相同，无人机在第0 s开始以速度30 m/s飞行，威胁机在第6 min启动，并且在第2.3 min进入本机避撞区范围，无人机根据学习得到的最优行为进行规避机动，采用增大左滚转加速的方式在短时间内完成实时路径规划。

连续动态威胁场景仿真结果如图11所示。

在连续威胁场景中，威胁1与本机第0 s同时启动，在第1.6 min进入本机避撞区范围，本机通过右滚转并拉升的方式完成规避；威胁2在第5 min启动，并在启动后第3.6 min进入本机避撞区范围，无人机通过左滚转实现有效规避。

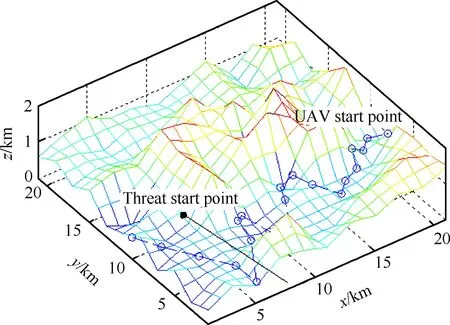
图10 单一动态威胁路径规划图Fig.10 Path planning in singly dynamic threat

图11 连续动态威胁路径规划图Fig.11 Path planning in continuously dynamic threats

3.4 多种类型威胁场景

无人机飞行过程中还可能面临敌方武器和大气气旋造成的禁飞区等威胁因素，在多种类型威胁场景中无人机路径规划难度更大。因此，实验中加入雷达、导弹和大气威胁以验证无人机经过学习后的路径规划能力。

本机启动时间和初速度与前3种场景相同，无人机通过地形威胁和动态威胁场景的学习具有较强的路径规划能力。由仿真结果图12可得，无人机有效规避大气威胁造成的禁飞区域；同时，分别以较大滚转加速的左滚转和右滚转机动实现对雷达威胁和导弹威胁的规避；并且在接近目标点时通过连续左滚转方式规避连续动态威胁。

仿真结果表明，无人机通过GA-OCPA学习系统的学习和经验知识的积累，能够在不同威胁场景下采取最优规避机动措施，以最小的代价完成实时路径规划，提高了无人机飞行的空域资源利用率和安全系数。

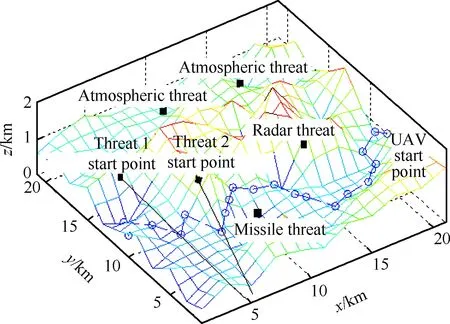
图12 多种类型威胁路径规划图Fig.12 Path planning in the multiple types of threats

4 结 论

1) 针对现有路径规划方法不能满足无人机飞行过程中应对突发威胁的问题，提出GA-OCPA学习系统，证明了其具有良好的自学习能力和自组织能力，且收敛时间短。

2) 建立无人机空间三维动态避撞区模型，分析了避撞区发生变化的影响因素，提出无人机可通过多种规避动作应对威胁，进而提高其飞行安全系数和空域利用率。

3) 无人机通过学习系统对路径规划过程中的规避机动行为进行学习，并建立行为知识库，多种场景仿真验证无人机的学习效果，证明了GA-OCPA学习系统对于无人机路径规划具有适用性和有效性。

致 谢

感谢空军工程大学信息与导航学院杨霄鹏副教授对本文无人机避撞技术及相关内容的指导，同时感谢北京航空航天大学电子信息工程学院刘雨帆硕士对本文系统学习理论的建议。

[1] KAVRAKI L E, SVESTKA P, LATOMBE J C, er al. Randomized preprocessing of configuration space for fast path planning[C]∥IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 1994: 3020-3026.

[2] XIAO Q K, GAO X G, FU X W, et al. New local path replanning algorithm for unmanned combat air vehicle[C]∥Proceedings of the 6th World Congress on Intelligent Control and Automation. Piscataway, NJ: IEEE Press, 2006: 4033-4037.

[3] 丁家如, 杜昌平, 赵耀, 等. 基于改进人工势场法的无人机路径规划算法[J]. 计算机应用, 2016, 36(1): 287-290.

DING J R, DU C P, ZHAO Y, et al. Path planning algorithm for unmanned aerial vehicles based on improved artificial potential field[J]. Journal of Computer Applications, 2016, 36(1): 287-290 (in Chinese).

[4] CHEN T B, ZHANG Q S. Robot motion planning based on improved artificial potential field[C]∥3rd 2013 International Conference on Computer Science and Network Technology. Piscataway, NJ: IEEE Press, 2013: 1208-1211.

[5] JU H S, TSAI C C. Design of intelligent flight control law following the optical payload[C]∥Proceedings of the 2004 IEEE International Conference on Networking, Science & Network. Piscataway, NJ: IEEE Press, 2004: 761-766.

[6] LUGO G I, FLORES G, SALAZAR S, et al. Dubins path generation for a fixed wing UAV[C]∥International Conference on Unmanned Aircraft Systems. Piscataway, NJ: IEEE Press, 2014: 339-346.

[7] LEE D, SHIM D H. Spline-RRT*based optimal path planning of terrain following flight for fixed-wing UAVs[C]∥The 11th International Conference on Ubiquitous Robots and Intelligence. Piscataway, NJ: IEEE Press, 2014: 257-261.

[8] GUAN X M, ZHANG X J, WEI J, et al. A strategic conflict avoidance approach based on cooperative coevolutionary with the dynamic grouping strategy[J]. International Journal of Systems Science, 2016, 47(9): 1995-2008.

[9] 魏瑞轩, 何仁珂, 张启瑞, 等. 基于Skinner理论的无人机应急威胁规避方法[J]. 北京理工大学学报, 2016, 36(6): 620-624.

WEI R X, HE R K, ZHANG Q R, et al. Skinner-based emergency collision avoidance mechanism for UAV[J]. Transactions of Beijing Institute of Technology, 2016, 36(6): 620-624 (in Chinese).

[10] LIN Z J, LIU H T. Consensus based on learning game theory with a UAV rendezvous application[J]. Chinese Journal of Aeronautics, 2015, 28(1): 191-199.

[11] ZHANG B, LIU W, MAO Z, et al. Cooperative and Ge-ometric Learning Algorithm(CGLA) for path planning of UAVs with limited information[J]. Automatica, 2014, 50(3): 809-820.

[12] ZHANG B, MAO Z, LIU W, et al. Geometric reinforcement learning for path planning of UAVs[J]. Journal of Intelligent & Robotic Systems, 2015, 77(2): 391-409.

[13] 郝钏钏, 方舟, 李平. 基于Q学习的无人机三维航迹规划算法[J]. 上海交通大学学报, 2012, 46(12): 1931-1935.

HAO C C, FANG Z, LI P. A 3-D route planning algorithm for unmanned aerial vehicle based on Q-learning[J]. Journal of Shanghai Jiaotong University, 2012, 46(12): 1931-1935 (in Chinese).

[14] ZHAO Y, LI W, SHI P. A real-time collision avoidance learning system for unmanned surface vessels[J]. Neurocomputing, 2016, 182: 255-266.

[15] WOLF R, HEISENBERG M. Basic organization of operant-behavior as revealed in drosophila flight orientation[J]. Journal of Comparative Physiology A, 1991: 169(6): 699-705.

[16] HWANG W S, WENG J. Hierarchical discriminant regression[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1277-1293.

[17] WENG J, HWANG W S. Incremental hierarchical discriminant regression[J]. IEEE Transactions on Neural Networks, 2013, 56(11): 2745-2761.

[18] KNEPPER R A, MASON M T. Realtime informed path sampling for motion planning search[J]. International Journal of Robotics Research, 2017, 31(11): 1231-1250.

[19] 张军. 空域监视技术的新进展及应用[J]. 航空学报, 2011, 32(1): 1-14.

ZHANG J. New development and application of airspace surveillance technology[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 1-14 (in Chinese).

[20] MELEGA M, LAZARUS S, SAVVARIS A, et al. Multiple threats sense and avoid algorithm for static and dynamic obstacles[J]. Journal of Intelligent & Robotic Systems, 2015, 77(1): 630-635.

[21] CHEN Y, YU J, MEI Y, et al. Modified central force optimization (MCFO) algorithm for 3D UAV path planning[J]. Neurocomputing, 2016, 171: 878-888.

UAVpathplanningbasedonGA-OCPAlearningsystem

LIUXin1,*,YANGXiaopeng1,LIUYufan2,YAOKun1

1.InformationandNavigationInstitute,AirForceEngineeringUniversity,Xi’an710077,China2.SchoolofElectronicsandInformationEngineering,BeihangUniversity,Beijing100083,China

Tosolvetheproblemofdeficiencyinreal-timelinessandapplicabilityofpathplanningfortheUnmannedAerialVehicle(UAV)intheunknownairspace,thereal-timepathplanningoftheUAVissimulatedasaself-learningbehaviorundertheconditionofexternalstimuli,basedonthebiologicaloperantconditioningtheory.TheprobabilisticautomatoniscombinedwiththegeneticalgorithmtoconstructalearningsystemofGeneticAlgorithm-OperantConditioningProbabilisticAutomaton(GA-OCPA)accordingtotheSkinneroperantconditioning.TheUAVs’evasionmaneuveringflightspeed,rollingaccelerationandclimbingaccelerationaretakenasthelearningbehaviorsofthesystem,andtheprobabilityofselectionandindividualfitnessarecalculatedaftereachlearningattempt.Theoptimalpathcanthenbeobtainedbysearchingforthebestbehaviorusingthegeneticalgorithm.TheknowledgebaseofthebestlearnedbehaviorsisestablishedusingIncrementalHierarchicalDiscriminantRegression(IHDR),andthematchingmappingbetweenthethreatstateandpathplanningisthenformed.TheresultshowstheviabilityandapplicabilityoftheGA-OCPAlearningsystemforUAVpathplanning.

UnmannedAerialVehicle(UAV);pathplanning;geneticalgorithm;operantconditioning;probabilisticautomaton

2017-03-27；Revised2017-06-12；Accepted2017-07-17；Publishedonline2017-07-232103

URL：http://hkxb.buaa.edu.cn/CN/html/20171127.html

s：NationalNaturalScienceFoundationofChina(61202490);AeronauticalScienceFoundationofChina(20150896010)

.E-mailkdyliuxin@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321275

V249.1

A

1000-6893(2017)11-321275-11

2017-03-27；退修日期2017-06-12；录用日期2017-07-17；< class="emphasis_bold">网络出版时间

时间：2017-07-232103

http://hkxb.buaa.edu.cn/CN/html/20171127.html

国家自然科学基金(61202490)； 航空科学基金(20150896010)

.E-mailkdyliuxin@163.com

刘鑫，杨霄鹏，刘雨帆，等．基于GA-OCPA学习系统的无人机路径规划方法J．航空学报,2017,38(11):321275.LIUX,YANGXP,LIUYF,etal.UAVpathplanningbasedonGA-OCPAlearningsystemJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):321275.

(责任编辑：苏磊)