3R-3URU可展单元机构及其在构架式可展天线中的应用

刘文兰，许允斗, 2，姚建涛, 2，陈亮亮，王辉，赵永生, 2,*

1.燕山大学 河北省并联机器人与机电系统实验室，秦皇岛 066004 2.燕山大学 先进锻压成型技术与科学教育部重点实验室，秦皇岛 066004 3.中国空间技术研究院 西安分院，西安 710100

3R-3URU可展单元机构及其在构架式可展天线中的应用

刘文兰1，许允斗1, 2，姚建涛1, 2，陈亮亮1，王辉3，赵永生1, 2,*

1.燕山大学 河北省并联机器人与机电系统实验室，秦皇岛 066004 2.燕山大学 先进锻压成型技术与科学教育部重点实验室，秦皇岛 066004 3.中国空间技术研究院 西安分院，西安 710100

提出了一种空间单自由度(DOF)可展单元机构3R-3URU。首先，基于螺旋理论和修正的G-K公式分析了RURUR单闭环机构的自由度，建立了该机构中主动关节和被动关节速度之间的解析关系式，基于此关系式和3个RURUR机构共用首尾转动副的结构特点推导了3R-3URU单元机构的自由度，得到了3R-3URU机构具有1个自由度时各运动副的方向和位置满足的几何关系式。其次，将3R-3URU机构应用于3RR-3RRR四面体可展单元及其组成的球面构架式可展天线中，得到了具有收拢和调姿两种自由度的新型可展机构。最后，利用Adams软件对3R-3URU可展单元机构的自由度和其在四面体构架式可展天线中的应用进行了仿真验证。该3R-3URU可展单元机构具有单自由度、铰链种类少、结构简单等优点，可用于曲面构架式可展天线的支撑机构中，实现大折叠比。

可展单元；自由度；螺旋理论；折叠比；可展天线

可展机构在储存和运输时处于收拢状态，占据运载装置较小的空间，当需要工作时可完全展开。因具有这种特点可展机构在航空航天、新型建筑等领域有广泛的应用前景，是当今国际上的一个研究热点。

自可展机构起源以来，国内外学者已提出了多种可展机构。文献[1-6]基于剪叉机构提出了不同的可展机构；李波和杨毅[7]研究了一种可展开平板天线支撑机构的结构优化问题；文献[8-11]各提出了一种平面可展机构；杨毅和丁希仑[12-13]分别基于7杆闭环机构和空间多面体向心机构提出了一种四棱锥可展单元和一种新型六面体机构，可组合成大型平面可展机构和伸展臂；Ding等[14]提出了一种新型的三棱柱可展机构；Vu等[15]提出了一类空间可展单元结构；陈向阳和关富玲[16]提出了一种利用伸缩杆驱动的六棱柱可展单元，在此单元的基础上设计了一种大型构架式抛物面天线；关富玲等[17-18]提出了一种由四面体可展单元组成的构架式可展天线机构；文献[19-21]分别研究了Bennett、Bricard和Myard连杆机构在可展机构中的应用。尽管目前已提出多种可展单元，但应用于航天构架式可展天线的为数不多，其中，四面体单元应用最为广泛，然而仅含转动铰链的四面体构架式可展天线[17-18,22-23]和含特殊材料(如形状记忆聚合物材料)铰链的四面体构架式可展天线[24]主要靠铰链间隙或杆件弹性变形达到理想收拢末态，这里理想收拢末态是指构架式可展天线反射面和背架层的节点构件均达到彼此靠拢的状态。针对此，本文提出一种空间可展单元3R-3URU(R和U分别表示转动副和虎克铰)，将其应用于仅含转动铰链的四面体构架式可展天线的支撑机构中，克服原机构靠杆件弹性变形和铰链间隙达到理想收拢末态的不足。

空间可展单元机构具有高度非线性和耦合性，其自由度分析比较困难，目前针对此类机构自由度分析方法的研究文献较少，主要有去除不影响机构自由度的运动子链法[25-26]、拆分杆组法[27]、等效法[23,28-29]、分流标记法[30]、基于多面体框架理论的方法[31]，等等，其通用性均不够强。本文拟结合3R-3URU单元的结构约束特点，采用传统自由度分析方法——螺旋理论和修正的G-K公式分析该空间多环耦合机构的自由度。

1 3R-3URU可展单元机构的结构及自由度分析

1.1 结构组成

3R-3URU可展单元机构由1个顶花盘、3根摇摆杆、6根连杆、6个转动副(R)和6个虎克铰(U)组成，如图1所示，其中，U副用两个轴线相交的R副表示。3根摇摆杆等长，其上端分别通过转动副R4、R5和R6与顶花盘连接，且R4、R5和R6副的轴线共面；摇摆杆1下端通过虎克铰U11和U32分别与连杆11和连杆32相连，摇摆杆2下端通过虎克铰U12和U21分别与连杆12和连杆21相连，摇摆杆3下端通过虎克铰U31和U22分别与连杆31和连杆22相连，转动副R1连接的连杆11和连杆12等长，转动副R2连接的连杆21和连杆22等长，转动副R3连接的连杆31和连杆32等长。

记3根摇摆杆的轴线相交于点H，其下端点分别为I、J和K，点O为三角形IJK的外心，则R4、R5和R6副的轴线分别垂直于平面IOH、JOH和KOH，R1副的轴线与连杆11和连杆12的轴线均垂直，R2副的轴线与连杆21和连杆22的轴线均垂直，R3副的轴线与连杆31和连杆32的轴线均垂直，虎克铰Uij(i=1,2,3,j=1,2)靠近连杆的转轴沿连杆轴线方向、另一个转轴与转动副Ri的轴线平行。不失一般性，R1、R2和R3副的轴线与平面IJK不平行。

任意一个球副(S)的运动与空间3个轴线相交于一点的R副的运动等效，因此，3R-3URU可展单元机构中，虎克铰Ui1和Ui2靠近连杆的转轴以及转动副Ri可由一个S副代替，得到3R-3URU可展单元机构的等效机构3R-3RSR，如图2所示。

图1 3R-3URU可展单元机构简图Fig.1 Schematic of 3R-3URU deployable mechanism

图2 3R-3URU可展单元的等效机构Fig.2 Equivalent mechanism of 3R-3URU deployable unit

1.2 自由度分析

3R-3URU可展单元机构可以看做是由3个单闭环机构RURUR共用首尾两端的R副连接而成，即由单闭环机构R4U11R1U12R5、R5U21R2U22R6和R6U31R3U32R4组成。在分析3R-3URU机构的自由度前先选取其中一个单闭环机构进行研究，如图3所示，在虎克铰U11和U12中心连线的中点O1建立坐标系O1-x1y1z1，x1轴沿虎克铰U11和U12中心的连线，z1轴与平面IJK的法线OH平行，y1轴根据右手定则确定。

在连杆11和连杆12不共线的任意位形下，记运动副R4、U11、R1、U12和R5的中心在坐标系O1-x1y1z1下的坐标分别为(-x4,y4,z)、(-x11,0,0)、(0,y1,z1)、(x11,0,0)和(x4,y4,z)，记转动副R4的轴线与x1轴的夹角为α1,则运动副R4、U11、R1、U12和R5的单位运动螺旋在O1-x1y1z1下可表示为

(1)

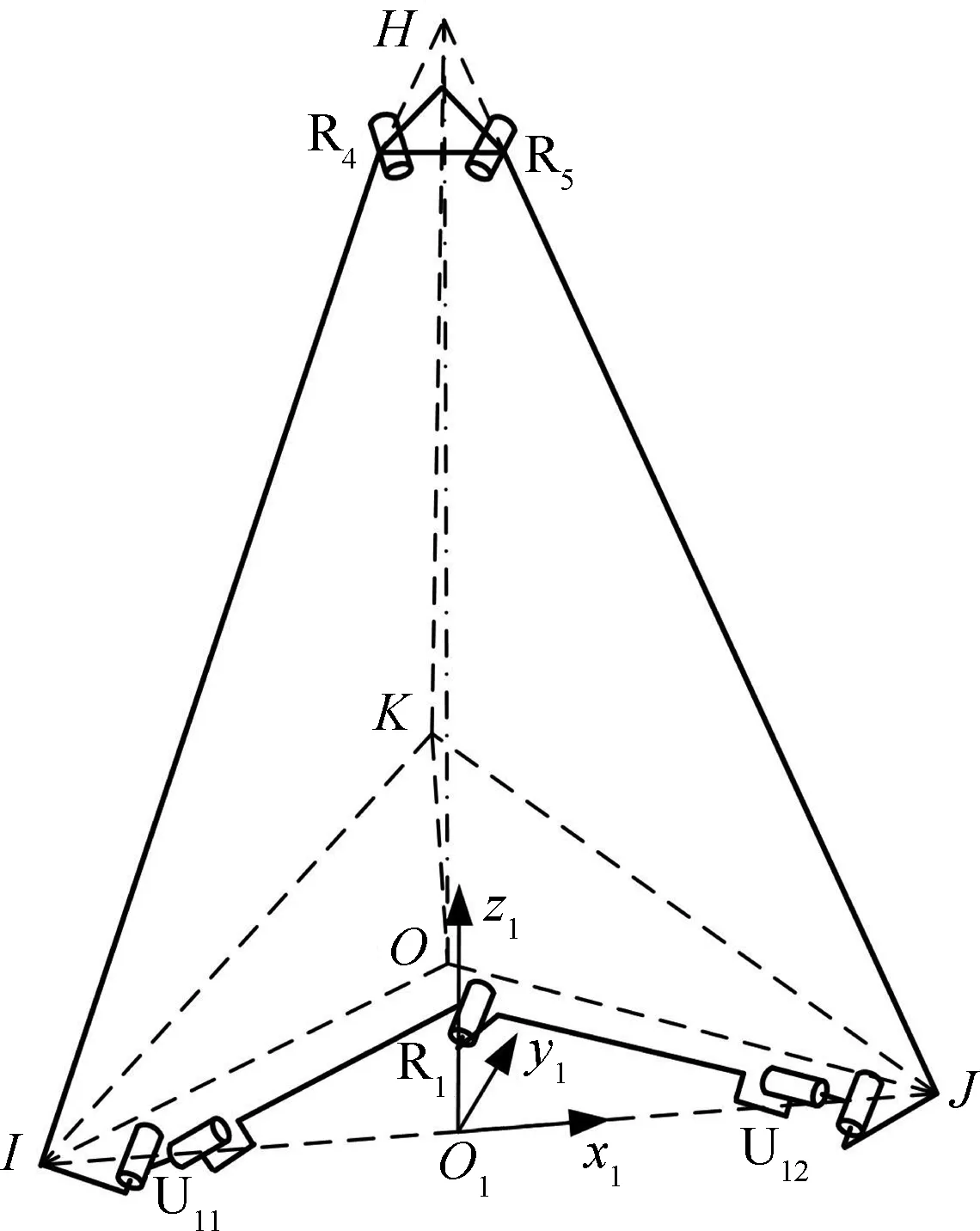
图3 RURUR单闭环机构简图Fig.3 Schematic of single closed-loop mechanism RURUR

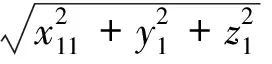
求上述运动螺旋系的反螺旋可得单闭环机构R4U11R1U12R5的约束螺旋为

(2)

式(2)表明单闭环机构R4U11R1U12R5中不存在公共约束，则根据修正的G-K公式可得单闭环机构R4U11R1U12R5的自由度为

6×(5-5-1)+7=1

(3)

式中：M为机构自由度数；d为机构的阶数，且d=6-λ，λ为机构的公共约束数；n为包含机架在内的构件数；g为机构所含运动副个数；fk(k=1,2,…,g)为第k个运动副具有的单自由度数；v为冗余约束数；ξ为局部自由度数。

同理，可知单闭环机构R5U21R2U22R6和R6U31R3U32R4均具有1个自由度，根据其共用手尾两端R副的连接方式可得3R-3URU机构最多具有1个自由度。

假设转动副R4为驱动关节，在单闭环机构R4U11R1U12R5中驱动关节速度和被动关节速度满足：

q4O1$R4+wU11,1O1$U11,1+wU11,2O1$U11,2+

wR1O1$R1+wU12,1O1$U12,1+wU12,2O1$U12,2+

wR5O1$R5=06×1

(4)

式中：q4为驱动关节R4的速度；wU11,1和wU11,2为被动关节U11的速度；wU12,1和wU12,2为被动关节U12的速度；wR1和wR5分别为被动关节R1和R5的速度。

将式(4)变形为

J1ω1=-q4O1$R4

(5)

若6×6矩阵J1可逆，则由式(5)可得单闭环机构R4U11R1U12R5中所有被动关节的速度为

(6)

从式(6)可得单闭环机构R4U11R1U12R5中被动关节R5的速度为

(7)

根据3R-3URU机构的结构组成可知，单闭环机构R4U11R1U12R5的被动关节R5可以作为单闭环机构R5U21R2U22R6的驱动关节，单闭环机构R5U21R2U22R6的被动关节R6可以作为单闭环机构R6U31R3U32R4的驱动关节，则有

(8)

(9)

式中：wR6和wR4分别为被动关节R6和R4的速度；O2$R5和O3$R6分别为转动副R5和R6在坐标系O2-x2y2z2和O3-x3y3z3下的单位运动螺旋，其中，坐标系O2-x2y2z2和O3-x3y3z3在单闭环机构R5U21R2U22R6和R6U31R3U32R4中的建立方式与O1-x1y1z1类似；J2由运动副U21、R2、U22和R6在O2-x2y2z2下的单位运动螺旋组成；J3由运动副U31、R3、U32和R4在O3-x3y3z3下的单位运动螺旋组成。

将式(7)和式(8)代入式(9)可得单闭环机构R6U31R3U32R4中被动关节R4的速度为

(10)

(11)

时，3R-3URU机构具有1个自由度。

将所有运动副的单位螺旋表达式代入式(11)可得该式成立，因此，3R-3URU机构具有1个自由度。若固定顶花盘，则在驱动关节R4的作用下3根摇摆杆分别绕转动副R4、R5和R6同步转动。

式(11)左边的表达式仅含3R-3URU机构各运动副的单位螺旋，说明3R-3URU机构是否具有1个自由度取决于各运动副的位置和方向之间的几何关系是否满足式(11)。

当连杆11和连杆12共线时，虎克铰U11靠近连杆11的转动副和虎克铰U12靠近连杆12的转动副共轴，存在1个局部自由度，此时机构自由度变为

6×(5-5-1)+7-1=0

(12)

式(12)表明当连杆11和连杆12共线时，单闭环机构R4U11R1U12R5的自由度为0，根据3R-3URU机构的结构特点可得其自由度也为0，该位形即为3R-3URU机构在工作空间内的边界奇异位形。同理，当连杆21和连杆22共线或连杆31和连杆32共线时，3R-3URU单元机构的自由度也为0。

综上，3R-3URU单元机构在其工作空间内的边界奇异位形下自由度为0，其他任意位形下具有1个自由度。

建立3R-3URU机构的仿真模型，如图4所示，其中摇摆杆和底面花盘之间固接。在转动副R4上添加驱动使其转动速度为0.5(°)/s，则在该驱动作用下3R-3URU机构实现了确定的运动。仿真38 s，测得转动副R4～R6的转角变化如图5所示。

图5表明仅在1个驱动作用下3根摇摆杆分别绕转动副R4、R5和R6同步转动，验证了前述对3R-3URU机构自由度分析的正确性。

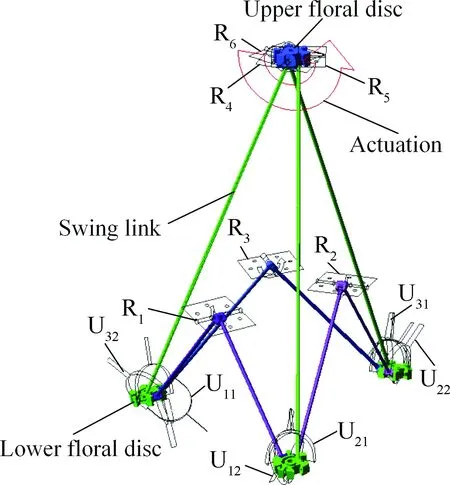
图4 3R-3URU机构的仿真模型Fig.4 Simulation model of 3R-3URU mechanism

图5 转动副R4～R6的转角变化Fig.5 Angular displacements of joints R4-R6

2 在构架式可展天线中的应用

2.1 在3RR-3RRR四面体可展天线中的应用

根据文献[27]可知图6所示的3RR-3RRR四面体可展单元机构具有1个自由度，若固定其顶花盘L，选取任意一个R副为驱动关节，则在驱动作用下底面花盘A、B和C向四面体单元底面的法线P1P2同步靠近/远离，在运动过程中3个底面花盘只发生移动运动，其姿态始终保持不变。当多个3RR-3RRR四面体单元组成构架式可展天线的支撑机构(以下简称为构架式可展天线机构)时，由于天线反射面一般为球面或抛物面等曲面，在天线的完全展开状态，支撑机构位于反射面的花盘在一个曲面上，背架层的花盘位于另一曲面上。因整个机构只有一个收拢自由度，在收拢过程中反射面和背架层花盘同步移动，当反射面花盘彼此靠拢时，背架层花盘两两之间还相距较远[27]，导致机构未达到理想折叠比。例如，图7所示的由3个3RR-3RRR四面体可展单元(① 四面体单元L-ABC、② 四面体单元N-ADE、③ 四面体单元M-AGF)组成的小型球面构架式可展天线机构，在完全展开状态，反射面花盘A、B、C、D、E、F、G位于球面上，背架层花盘L、M、N位于另一球面上，为提高机构整体刚度，在不影响机构原有自由度的前提下，背架层花盘两两之间用URS支链连接。

图6 3RR-3RRR可展单元机构简图Fig.6 Schematic of 3RR-3RRR deployable mechanism

图7 3个3RR-3RRR单元组成的球面机构Fig.7 Mechanism with a spherical surface composed of three 3RR-3RRR units

图8 图7所示机构完全展开状态的三维模型Fig.8 Three-dimensional model of mechanism shown in Fig.7 in expanded configuration

图8为3个3RR-3RRR单元组成的球面可展机构在完全展开状态的三维模型，反射面花盘的包络圆半径R0=0.521 9 m，背架层花盘的包络圆半径r0=0.385 8 m，背架层和反射面之间的最大距离h0=0.561 7 m。固定反射面中心花盘A，在单驱动作用下反射面和背架层花盘均保持姿态不变向目标收拢轴线同步移动，机构收拢末态如图9所示，该位形下反射面花盘的包络圆半径Ru=0.075 5 m，背架层花盘的包络圆半径ru=0.138 1 m，背架层和反射面之间的最大距离hu=0.617 9 m。从图9可以看出，在该机构的收拢末态反射面和背架层花盘仍位于球面上，且反射面花盘已彼此靠拢，而背架层花盘间还有一定的距离，机构的收拢效果不理想。

按照可展机构在完全展开状态和收拢末态所占空间的比值计算该机构的折叠比，则3个3RR-3RRR单元组成的球面可展机构的折叠比λ1为

16.078 7

(13)

根据本文1.2节对3R-3URU机构自由度的分析可知，该机构中与转动副R4、R5和R6相连的杆件可分别绕R4、R5和R6转动实现姿态的调整，因此，结合3RR-3RRR机构和3R-3URU机构得到具有收拢和调姿两种自由度的3RR-3URU机构，如图10所示，其中，转动副R4和R7的轴线相互平行、转动副R5和R8的轴线相互平行、转动副R6和R9的轴线相互平行。

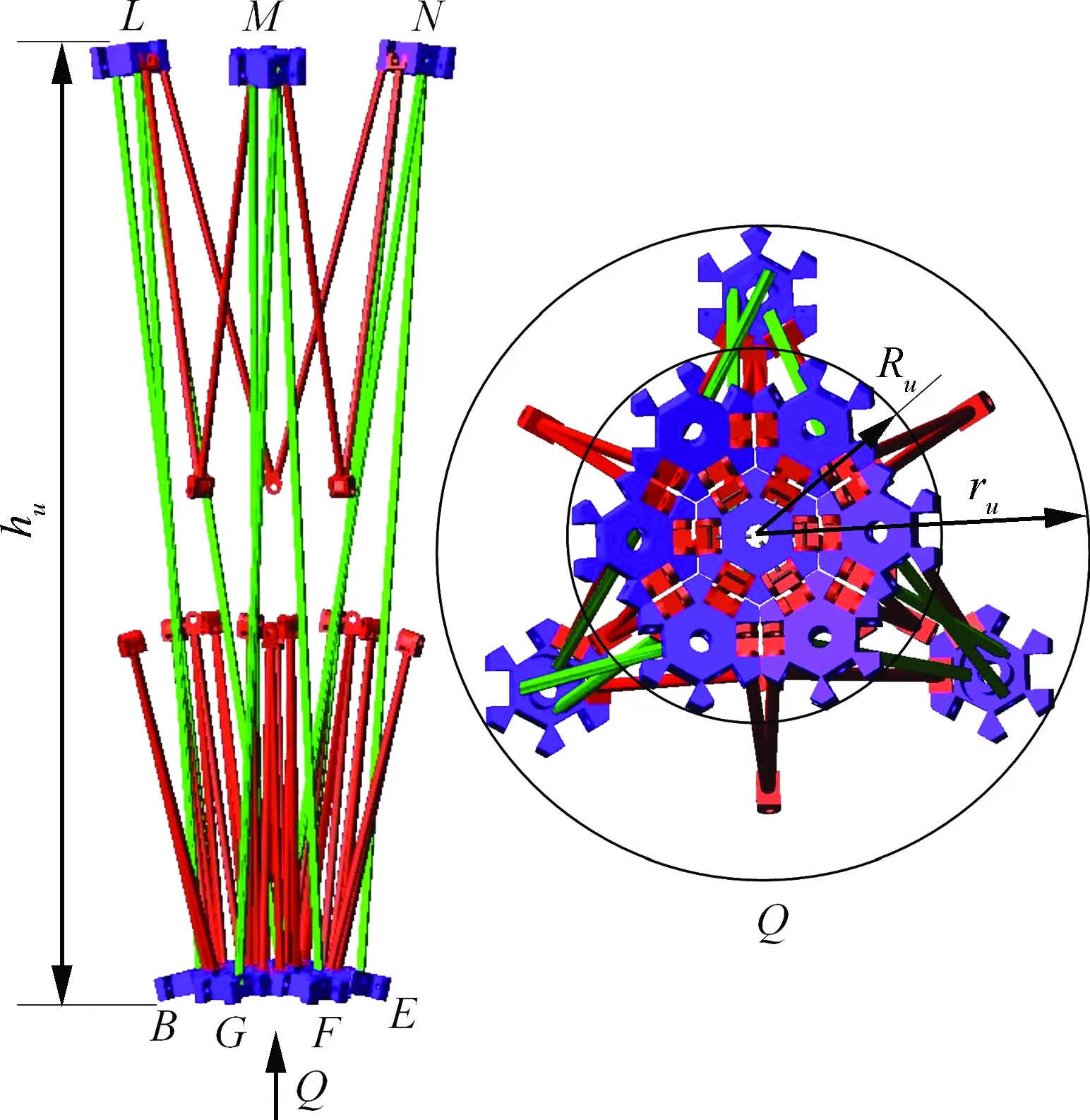
图9 图8所示机构的收拢末态Fig.9 Folded configuration of mechanism shown in Fig.8

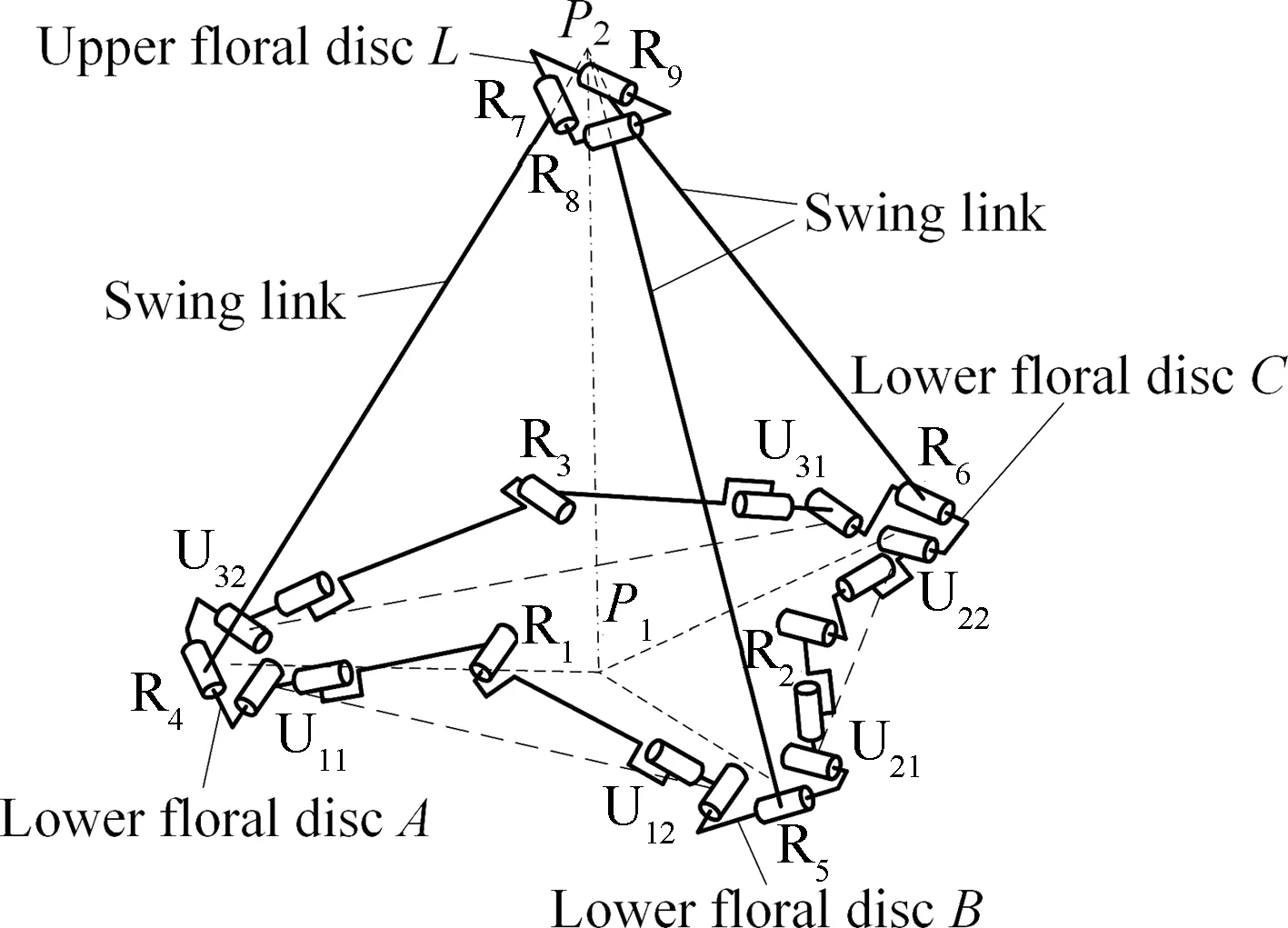
图10 3RR-3URU机构简图Fig.10 Schematic of 3RR-3URU mechanism

图11 3RR-3URU机构的结构分解图Fig.11 Structure decomposition of 3RR-3URU mechanism

根据文献[28]对多环耦合机构的自由度分析方法，图10所示机构可以拆分为单闭环机构R7R4U11R1U12R5R8、杆组R9R6U22R2U21和杆组U31R3U32，如图11所示，通过分析后一个杆组对前一个杆组自由度的影响即可得到3RR-3URU单元机构的自由度。

根据修正的G-K公式易得图11中单闭环机构R7R4U11R1U12R5R8具有3个自由度。杆组R9R6U22R2U21为7自由度串联运动链，将其添加到单闭环机构R7R4U11R1U12R5R8上，不会引入约束但增加了1个局部自由度，最终得到4自由度机构。在这4自由度机构中，将花盘A视为机架，则花盘B通过分支U11R1U12和含闭环子链的分支R4R7-(R8R5U21R2U22R6R9) 与机架A相连。根据反螺旋理论可得分支U11R1U12施加给花盘B一个与转动副R1轴线重合的约束力，含闭环子链的分支R4R7-(R8R5U21R2U22R6R9)施加给花盘B一个与转动副R4和R5的轴线均垂直的约束力偶、一个过转动副R4与R5轴线交点和转动副R7与R8轴线交点的约束力，则花盘B相对于机架A具有两个转动和一个移动自由度，其中，两个转动轴线位于与R4和R5轴线确定平面平行的平面内，移动轴线沿虎克铰U11和U12中心的连线。同理可得在该4自由度机构中，花盘C相对于机架A也具有两个转动和一个移动自由度，其中，两个转动轴线位于与R5和R6轴线确定平面平行的平面内，移动轴线沿虎克铰U21和U22中心的连线。由于整个机构具有4个自由度，其独立的关节参数只有4个，因此，花盘B和C的4个转动自由度中只有两个是独立的，另外，花盘B和C相对于机架A的两个移动自由度是独立的。杆组U31R3U32为5自由度运动链，将其添加到上述4自由度机构的花盘B和C之间，限制了两花盘沿R3轴线方向的相对移动，使花盘B和C的两个移动自由度变得相关，即杆组U31R3U32引入了1个实约束。

综上，在3RR-3URU单元机构中不存在公共约束和虚约束，根据G-K公式可得3RR-3URU单元机构的自由度为

6×12-(5×9+4×6)=3

(14)

式中：uq(q=1,2,…,15)为第q个运动副引入的约束数。式(14)表明3RR-3URU单元机构具有3个自由度，花盘B和C除具有向机架A的移动自由度外还具有转动自由度，即在3RR-3URU机构中花盘B和C相对于机架A的姿态可变。下文中将花盘的移动自由度和转动自由度分别称为收拢自由度和调姿自由度。

图12 3个3RR-3URU单元组成的球面机构简图Fig.12 Schematic of mechanism with a spherical surface composed of three 3RR-3URU units

由3个3RR-3URU单元机构组成的球面构架式可展天线机构(单元之间通过URU支链连接)如图12所示，为提高机构整体刚度，背架层花盘两两之间仍采用URS支链连接。该机构可以视做是在第1个单元机构的基础上先后添加第2个和第3个单元机构，然后在花盘C和D、花盘E和F、花盘B和G之间依次添加杆组URU，最后在背架层花盘L和M、花盘L和N、花盘N和M之间添加杆组URS得到的。

将花盘A视为机架，在第1个3RR-3URU单元机构的基础上依次添加第2个和第3个单元机构，由于这3个单元机构仅共用机架，其自由度相互独立，则3个3RR-3URU单元共用机架花盘A得到的机构具有9个自由度。根据前述对单个3RR-3URU机构的自由度分析可知，在3个3RR-3URU单元共用机架A构成的机构中，花盘B和C的移动自由度相关，花盘D和E的移动自由度相关，花盘F和G的移动自由度相关。由于杆组URU提供1个约束限制其两端U副连接的杆件沿R副轴线方向的相对移动，故在花盘C和D之间添加杆组URU后，花盘C和D的移动变得相关，在花盘E和F之间添加杆组URU后，花盘E和F的移动变得相关，从而可得花盘B、C、D、E、F、G向机架A的移动是相关的，此时再在花盘B和G之间添加杆组URU，引入了1个虚约束。杆组URS为6自由度运动链，在背架层花盘间添加杆组URS不会引入约束。

综上，由3个3RR-3URU单元机构组成的球面可展天线机构在非边界奇异位形，存在1个虚约束(即冗余约束)，不存在公共约束和局部自由度，则根据修正的G-K公式可得该机构的自由度为

6×(43-54-1)+78+1=7

(15)

式(15)表明3个3RR-3URU单元机构组成的球面可展机构具有7个自由度，反射面花盘除具有向机架A的收拢自由度外还具有调姿自由度。

2.2 仿真验证

建立3RR-3URU机构的仿真模型，如图13所示，其中摇摆杆和底面花盘之间通过R副连接，初始状态3个底花盘的平面不平行。根据前述分析可知3RR-3URU机构具有3个自由度，因此，为保证机构具有确定的运动，至少添加3个驱动。

为方便验证3RR-3URU单元机构的收拢自由度和调姿自由度，仿真时设定驱动值让底面花盘完成收拢运动后再进行调姿运动，该机构在收拢末态和调姿末态底面花盘的姿态如图14所示。

3个3RR-3URU单元组成的球面可展天线机构在半收拢状态的仿真模型如图15所示，为保证该机构实现确定的运动，其仿真模型中至少添加7个驱动。为验证该机构的收拢自由度和调姿自由度，设定各驱动大小使机构达到图9所示的收拢末态后，保持收拢驱动为固定值，让调姿驱动继续作用，使反射面花盘绕其与摇摆杆连接的R副转动实现姿态的调整，在调姿过程中摇摆杆带动背架层花盘继续向收拢目标轴线靠拢，最终背架层花盘也紧密靠拢，如图16所示。

选取ZYX欧拉角描述3个3RR-3URU单元组成的球面可展天线机构在收拢过程中各花盘相对于机架花盘A的姿态。以花盘C为例，测得其质心坐标系相对于花盘A质心坐标系的欧拉角如图17所示(α、β、γ分别表示绕X、Y、Z轴的转角)。

图13 3RR-3URU机构的仿真模型Fig.13 Simulation model of 3RR-3URU mechanism

图14 3RR-3URU机构底面花盘的姿态Fig.14 Orientation of lower floral discs of 3RR-3URU mechanism

图15 图12所示机构在半收拢状态的仿真模型Fig.15 Simulation model of mechanism shown in Fig.12 in its middle-folded configuration

图16 图12所示机构的完全收拢状态Fig.16 Completely folded configuration of mechanism shown in Fig.12

从图17可以看到在0～33 s内α、β和γ始终保持初始值不变，在第33 s之后α、β和γ均发生非线性变化(其中，β近似线性变化)，说明0～33 s为图12所示机构的收拢过程，期间花盘C仅发生移动运动，在第33 s反射面花盘彼此靠拢，之后反射面花盘开始调姿运动，在调姿过程中带动摇摆杆摆动，进而带动背架层花盘继续向目标收拢轴线运动，在第45 s背架层花盘也实现彼此靠拢，调姿运动结束。

图17 花盘C相对于花盘A的欧拉角Fig.17 Euler angles of floral disc C relative to disc A

在完全展开状态，3个3RR-3URU单元和3个3RR-3RRR单元组成的球面可展机构所占空间相同。在完全收拢状态，3个3RR-3URU单元组成的球面可展机构反射面花盘的包络圆半径Rv=0.077 3 m，背架层花盘的包络圆半径rv=0.063 6 m，背架层和反射面之间的最大距离hv=0.619 8 m，如图16所示，则3个3RR-3URU单元组成的球面可展机构的折叠比λ2为

37.773 9

(16)

对比式(13)和式(16)可以看到，与3RR-3RRR单元组成的球面可展机构相比，3RR-3URU单元组成的球面机构具有更大的折叠比，且球面构架式可展天线反射面的曲率越大，3RR-3URU机构具有大折叠比的优势越明显。

综上，由3RR-3URU机构组成的球面可展机构不仅具有收拢自由度还具有调姿自由度，可实现大折叠比。

3 结 论

1) 基于单闭环机构RURUR提出了一种空间可展单元机构3R-3URU，该单元机构具有单自由度且结构简单、铰链种类少。

2) 将3R-3URU机构应用于3RR-3RRR四面体球面构架式可展天线机构中，得到了具有收拢和调姿两种自由度的可展机构，克服了原机构折叠比小的缺点。

[1] AKGVN Y, GANTES C J, SOBEK W, et al. A novel adaptive spatial scissor-hinge structural mechanism for convertible roofs[J]. Engineering Structures, 2011, 33(4): 1365-1376.

[2] AKGVN Y, GANTES C J, KALOCHAIRETIS K E, et al. A novel concept of convertible roofs with high transformability consisting of planar scissor-hinge structures[J]. Engineering Structures, 2010, 32(9): 2873-2883.

[3] LANGBECKER T. Kinematic analysis of deployable scissor structures[J]. International Journal of Space Structures, 1999, 14(1): 1-15.

[4] ZHAO J S, CHU F L, FENG Z J. The mechanism theory and application of deployable structures based on SLE[J]. Mechanism and Machine Theory, 2009, 44(2): 324-335.

[5] SUN Y T, WANG S M, LI J F, et al. Mobility analysis of the deployable structure of SLE based on screw theory[J]. Chinese Journal of Mechanical Engineering, 2013, 26(4): 793-800.

[6] 李端玲, 张忠海, 于振. 球面剪叉可展机构的运动特性分析[J]. 机械工程学报, 2013, 49(13): 1-7.

LI D L, ZHANG Z H, YU Z. Kinematic characteristic analysis of spherical scissors deployable mechanisms[J]. Journal of Mechanical Engineering, 2013, 49(13): 1-7 (in Chinese).

[7] 李波, 杨毅. 星载平面可展天线支撑桁架的结构效率优化[J]. 航空学报, 2015, 36(12): 3853-3860.

LI B, YANG Y. Optimization for structure efficiency of a deployable spaceborne truss with flat panel antennas[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3853-3860 (in Chinese).

[8] CHERNIAVSKY A G, GULYAYEV V I, GAIDAICHUK V V, et al. Large deployable space antennas based on usage of polygonal pantograph[J]. Journal of Aerospace Engineering, 2005, 18(3): 139-145.

[9] CHU Z R, DENG Z Q, QI X Z, et al. Modeling and analysis of a large deployable antenna structure[J]. Acta Astronautica, 2014, 95(1): 51-60.

[10] WANG Y, LIU R Q, YANG H, et al. Design and deployment analysis of modular deployable structure for large antennas[J]. Journal of Spacecraft and Rockets, 2015, 52(4): 1101-1111.

[11] LU S N, ZLATANOV D, DING X L, et al. A new family of deployable mechanisms based on the Hoekens linkage[J]. Mechanism and Machine Theory, 2014, 73: 130-153.

[12] 杨毅, 丁希仑. 四棱锥单元平板式可展开收拢机构的运动特性分析[J]. 航空学报, 2010, 31(6): 1257-1265.

YANG Y, DING X L. Kinematic analysis of a plane deployable mechanism assembled by four pyramid cells[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1257-1265 (in Chinese).

[13] 杨毅, 丁希仑. 基于空间多面体向心机构的伸展臂设计研究[J]. 机械工程学报, 2011, 47(5): 26-34.

YANG Y, DING X L. Design and analysis of mast based on spatial polyhedral linkages mechanism along radial axes[J]. Journal of Mechanical Engineering, 2011, 47(5): 26-34 (in Chinese).

[14] DING X L, YANG Y, DAI J S. Design and kinematic analysis of a novel prism deployable mechanism[J]. Mechanism and Machine Theory, 2013, 63: 35-49.

[15] VU K K, RICHARD J Y, ANANDASIVAM K. Deployable tension-strut structures: from concept to implementation[J]. Journal of Constructional Steel Research, 2006, 62(3): 195-209.

[16] 陈向阳, 关富玲. 六棱柱单元可展抛物面天线结构设计[J]. 宇航学报, 2001, 22(1): 75-78.

CHEN X Y, GUAN F L. A large deployable hexapod paraboloid antenna[J]. Journal of Astronautics, 2001, 22(1): 75-78 (in Chinese).

[17] 杨玉龙, 关富玲, 侯国勇, 等. 基于结构解析模型法可展桁架天线结构初步设计[J]. 中国机械工程, 2009, 20(16): 1969-1973.

YANG Y L, GUAN F L, HOU G Y, et al. Deployable tetrahedral truss antenna initial structural design based on interpretative structural model analysis[J]. China Mechanical Engineering, 2009, 20(16): 1969-1973 (in Chinese).

[18] XU Y, GUAN F L. Structure-electronic synthesis design of deployable truss antenna[J]. Aerospace Science and Technology, 2013, 26(1): 259-267.

[19] CHEN Y, YOU Z. On mobile assemblies of Bennett linkages[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2008, 464(2093): 1275-1293.

[20] CHEN Y, YOU Z, TARNAI T. Three fold-symmetric Bricard linkages for deployable structures[J]. International Journal of Solids and Structures, 2005, 42(8): 2287-2301.

[21] QI X Z, DENG Z Q, LI B, et al. Design and optimization of large deployable mechanism constructed by Myard linkages[J]. CEAS Space Journal, 2013, 5(3): 147-155.

[22] 黄志荣, 宋燕平, 郑士昆, 等. 偏馈式构架反射器构型设计与展开协调性分析[J]. 机械科学与技术, 2016, 35(11): 1791-1796.

HUANG Z R, SONG Y P, ZHENG S K, et al. Analysis of configuration design and deployable coordination of offset-fed truss reflector[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(11): 1791-1796 (in Chinese).

[23] LIU W L, XU Y D, ZHAO Y S, et al. DOF and kinematic analysis of a deployable truss antenna assembled by tetrahedral elements[C]∥Lecture Notes in Electrical Engineering, 2017, 408: 855-868.

[24] FANG H, SHOOK L, LIN J K H, et al. A large and high radio frequency deployable reflector[C]∥3rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston, VA: AIAA, 2012.

[25] 李端玲, 戴建生, 张启先, 等. 一种变胞机构——魔术花球的自由度分析[J]. 机械工程学报, 2002, 38(9): 12-16.

LI D L, DAI J S, ZHANG Q X, et al. Mobility of a kind of metamorphic mechanism—magic ball[J]. Journal of Mechanical Engineering, 2002, 38(9): 12-16 (in Chinese).

[26] WEI G W, DING X L, DAI J S. Mobility and geometric analysis of the Hoberman switch-pitch ball and its variant[J]. Journal of Mechanisms and Robotics, 2010, 2(3): 031010-1-031010-9.

[27] 黄真, 刘婧芳, 李艳文. 论机构自由度——寻找了150年的自由度通用公式[M]. 北京: 科学出版社, 2011: 263-288.

HUANG Z, LIU J F, LI Y W. Mobility of mechanisms—a general formula of degree of freedom looking for 150 years[M]. Beijing: Science Press, 2011: 263-288 (in Chinese).

[28] 刘婧芳, 黄晓欧, 余跃庆, 等. 多环耦合机构末端件自由度计算的等效法[J]. 机械工程学报, 2014, 50(23): 13-19.

LIU J F, HUANG X O, YU Y Q, et al. Equivalent method of output mobility calculation for a novel multi-loop coupled mechanism[J]. Journal of Mechanical Engineering, 2014, 50(23): 13-19 (in Chinese).

[29] 许允斗, 刘文兰, 陈亮亮, 等. 构架式可展天线机构自由度分析——拆杆等效法[J]. 航空学报, 2017, 38(9): 421188.

XU Y D, LIU W L, CHEN L L, et al. Mobility analysis of a deployable truss-antenna mechanism—method based on link-demolishing and equivalent idea[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 421188 (in Chinese).

[30] 高慧芳, 刘婧芳, 黄晓欧. 基于独立运动分流标记法的多环耦合机构自由度分析方法[J]. 北京工业大学学报, 2015, 41(11): 1658-1664.

GAO H F, LIU J F, HUANG X O. Method of mobility calculation for a coupled mechanism based on independent motion shunting measurement[J]. Journal of Beijing University of Technology, 2015, 41(11): 1658-1664 (in Chinese).

[31] LALIERTE T, GOSSELIN C. Construction, mobility analysis and synthesis of polyhedra with articulated faces[J]. Journal of Mechanisms and Robotics, 2013, 6(1): 011007-1-011007-11.

Deployableunit3R-3URUanditsapplicationindeployabletrussantenna

LIUWenlan1,XUYundou1,2,YAOJiantao1,2,CHENLiangliang1,WANGHui3,ZHAOYongsheng1,2,*

1.ParallelRobotandMechatronicSystemLaboratoryofHebeiProvince,YanshanUniversity,Qinhuangdao066004,China2.KeyLaboratoryofAdvancedForging&StampingTechnologyandScienceofMinistryofEducation,YanshanUniversity,Qinhuangdao066004,China3.ChinaAcademyofSpaceTechnology(Xi’an),Xi’an710100,China

Aspatialdeployableunit3R-3URUwithoneDegreeofFreedom(DoF)isproposed.TheDoFofthesingleclosed-loopmechanismRURURisanalyzed,basedonthescrewtheoryandthemodifiedG-Kformula.TheanalyticalexpressionforthevelocitiesofactivejointsandpassivejointsofthemechanismRURURarethenestablished.AccordingtothevelocityexpressionandthestructuralcharacteristicthatthreeRURURmechanismssharetheirfirstandlastrevolutejoints,theDoFofthe3R-3URUmechanismisderived.Thegeometricalrelationshipamongthepositionsanddirectionsofalljointsisalsoobtainedwhenthe3R-3URUmechanismhasoneDoF.Noveldeployablemechanismsareobtainedbyapplyingthe3R-3URUmechanismtothe3RR-3RRRtetrahedralunitandadeployabletrussantennacomposedofthetetrahedralunits,andthenovelmechanismshavetwotypesofDoFsmovementandorientationadjustment.DoFanalysisandapplicationofthe3R-3URUdeployableunitareverifiedbytheAdamssoftware.Theproposeddeployableunit3R-3URUhastheadvantagesofoneDoF,simplestructure,andsingletypeofjoints,andcanbeappliedtothesupportingmechanismofdeployabletrussantennaswithacurvedsurfacetoachievealargefoldingratio.

deployableunit;DegreeofFreedom(DoF);screwtheory;foldingratio;deployableantenna

2017-03-27；Revised2017-04-27；Accepted2017-05-21；Publishedonline2017-06-021655

URL：http://hkxb.buaa.edu.cn/CN/html/20171130.html

s：NationalNaturalScienceFoundationofChina(51675458);KeyProjectofNaturalScienceFoundationofHebeiProvince(E2017203335);YouthTopTalentProjectofHebeiProvinceHigherEducation(BJ2017060)

.E-mailyszhao@ysu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421285

V243.4;TH112

A

1000-6893(2017)11-421285-11

2017-03-27；退修日期2017-04-27；录用日期2017-05-21；< class="emphasis_bold">网络出版时间

时间：2017-06-021655

http://hkxb.buaa.edu.cn/CN/html/20171130.html

国家自然科学基金(51675458)； 河北省自然科学基金重点项目(E2017203335)； 河北省高等学校青年拔尖人才计划项目(BJ2017060)

.E-mailyszhao@ysu.edu.cn

刘文兰，许允斗，姚建涛，等.3R-3URU可展单元机构及其在构架式可展天线中的应用J. 航空学报，2017,38(11):421285.LIUWL,XUYD,YAOJT,etal.Deployableunit3R-3URUanditsapplicationindeployabletrussantennaJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):421285.

(责任编辑：李世秋)