基于四杆机构单元的柔性铰链设计与尺寸优化

张静，寇子明

太原理工大学 机械工程学院，太原 030024

基于四杆机构单元的柔性铰链设计与尺寸优化

张静*，寇子明

太原理工大学 机械工程学院，太原 030024

针对柔性铰链存在的转动角度小和径向漂移大等问题，进行了大转角和高精度柔性铰链设计。利用四杆机构中曲柄摇杆机构的转角放大特性，以固化的四杆机构为变形模块，通过摇杆的小变形实现铰链的大转角运动。柔性铰链中固化的四杆机构为超静定结构，基于超静定结构理论进行了柔性单元的受力分析，并建立了柔性铰链的刚度模型，实现柔性铰链的分析和设计。根据设计方案选取设计变量，基于理论推导得到刚度建立目标函数，根据性能和几何边界建立约束条件，利用遗传算法对柔性铰链尺寸进行优化，并通过ANSYS进行了特定尺寸下柔性铰链变形和应力分析，验证了优化结果的正确性。

柔性铰链；四杆机构；大转角；刚度；优化

柔顺机构具有无间隙、无摩擦、无润滑的特性，在高精度、大行程的定位平台中应用较多[1-4]。柔性铰链作为柔顺机构的一种，由于其优良特性，在空间折展机构中也有一定的应用[5-6]。由于空间折展机构具有大折展比、长距离支撑的特点，其所含运动副较多，例如，美国NASA用于航天飞机对地进行高分辨率观测用的ADAM支撑臂中含有352个铰链。因此，柔性铰链在自驱动、高可靠性的折展机构中具有巨大的应用前景。但是由于平台和折展机构等要求柔性铰链的运动行程较大，一般柔性铰链很难满足折展机构的需求，因此，在保证柔性铰链精度的前提下提高运动行程成为柔性铰链广泛应用的前提。

柔性铰链的设计方法主要有FACT方法[7-10]、模块法[11-12]、拓扑优化法[13]、矩阵法和伪刚体法[14]等。FACT方法主要是基于旋量理论对运动和约束进行建模，得到完整的自由度与约束空间图谱，通过运动学等效实现运动台设计。Yu等基于此方法进行了一般柔顺机构型综合的系统研究[8]。Dibiasio和Hopkins考虑实际设计过程中存在的非理想约束，进行单自由度移动的自由空间对柔性约束的排布和弹性力学特性的敏感度的研究[10]。模块法则是进行系统功能划分，通过局部模块设计和组合实现机构设计。Kim等利用模块法进行转角放大柔顺机构的设计[11]，并进行单个模块与整体功能之间关系的研究[12]。而拓扑优化则是从空腔与实体的分布实现铰链的设计，Reddy等利用拓扑优化方法进行了特定运行轨迹的柔顺机构设计[13]。在柔性铰链刚度模型建立中较为常用的是伪刚体法，而其方法在建模过程是通过刚性连杆的位移逼近柔性梁的位移来实现柔性梁的刚性化，且对于曲梁的处理过程复杂[14]。曹玉岩等考虑铰链的超静定约束特点，利用虚功原理推导了环形柔性铰链的刚度模型，并对其进行优化[15]。

柔性铰链的种类繁多，按照结构形式主要分为杆约束和板约束两种柔性铰链。由于板约束下柔性铰链结构简单，且约束方式多样，因此对板约束下的柔性铰链研究较多。Soykasap等提出了用于天线折叠的片式柔性铰链[5]。Ciblak和Lipkin进行了大半径回转的柔性铰链设计[16]。Fowler等进行了大转角回转铰链的设计，其转角达到90°，中心漂移达到20 mm[17]。Yu等设计了用于平面微定位平台的大转角柔性系统[18]。Hopkins等介绍了生成平行柔性单元的方法，将有望用于下一代高精度柔性系统的设计[19]。Panas和Hopkins为了减小柔性单元的静态和动态损失，改进了双平行四边形约束下的柔性单元的设计[20]。邱丽芳等进行了疏齿型柔性铰链的研究[21]。赵山杉等进行了基于曲线柔性单元的柔性铰链研究[22]。

目前研究得到的柔性铰链仍存在转角较小、中心漂移较大的问题。因此，首先基于柔顺机构设计理论中的模块法，将具有转角放大特性的四杆机构进行刚化，以刚化的四杆机构为变形体进行柔性铰链的设计。其次，考虑到建立含曲梁结构柔性铰链的刚度模型的可行性和准确性，基于超静定结构的力学理论建立铰链的刚度模型，即为含有曲梁的柔性铰链刚度分析提供了一种途径，也为刚度模型的准确性提供了保障。最后基于柔性铰链的力学模型进行铰链刚度的优化，确定了铰链的结构参数和基本性能。

1 铰链刚度模型建立

1.1 柔性铰链方案

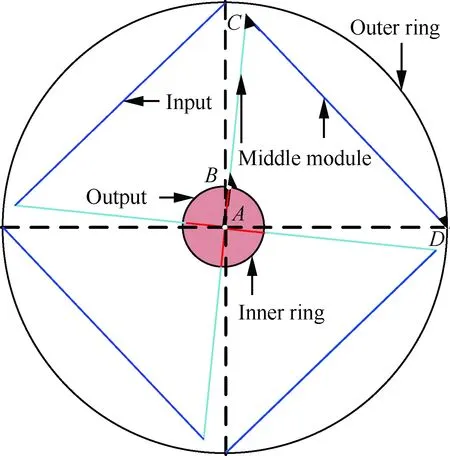
图1 柔性铰链设计方案Fig.1 Design program of flexible hinge

为了进行大转角和大平移刚度的柔性铰链设计，将具有转角放大特性的四杆机构即曲柄摇杆机构作为铰链的中间单元，进行柔性铰链方案设计。如图1所示，铰链由内圈、外圈和中间模块组成，曲柄摇杆机构ABCD为铰链的中间模块。曲柄摇杆机构中摇杆小转角与曲柄的大转角相对应，即在四杆机构ABCD中摇杆CD的小转角引起的小变形与曲柄AB的大转角对应，又由于曲柄AB与内圈固定，因此曲柄摇杆机构在铰链的转动过程中起到了转角放大的作用。四杆机构中各杆件绕回转铰链回转，各铰链处只存在接触力，而不存在弯矩。而在柔性铰链设计中，将四杆机构的各铰接点进行固化，对铰点的回转自由度进行约束。当外圈固定，内圈受到力矩作用时，内圈以曲柄上的A点为回转中心进行旋转。而当柔性铰链用于展开时，其摇杆存在变形，其弹性能驱动铰链旋转，即外圈固定，摇杆变形能驱动AB即内圈旋转。

1.2 中间模块受力分析

柔性四杆机构变形作用使内外圈产生了回转运动，因此中间模块的力学特性是铰链设计的核心。因此，为了进行铰链尺寸设计和结构优化，首先进行柔性四杆机构的受力分析。柔性四杆机构的简图如图2(a)所示，杆AB、杆BC、杆CD、杆AD的长度分别为a、b、c、d，4个杆件的初始角度分别为α、β、φ和0。当杆AB上受到弯矩M时，机构变形，实现内外圈之间的相对转动，杆AB、杆BC和杆CD相对于x轴转角分别为θAB=θ1+α、θBC=θ2+β和θCD=θ3+φ，其中θ1、θ2和θ3分别为杆AB、杆BC和杆CD变形过程中的转角。由于柔性四杆机构为超静定结构，取A点为静定基，将A点的赘余反力X1和X2加在静定基A上，如图2(b)所示。

图2 柔性四杆机构Fig.2 Flexible four-bar mechanism

由于此柔性四杆机构为二次超静定系统，因此，利用力法的正则方程，进行反力求解。系统在载荷M、X1和X2的作用下杆件AB的A端水平位移和竖直方向位移为零，与原简支边界相符。三力单独作用在A点引起的水平位移分别为δ1M、δ1X1、δ1X2,满足水平位移为零的条件是δ1M+δ1X1+δ1X2=0,其中δ1X1=δ11X1,δ1X2=δ12X2,其中δij表示由于Xj=1在Xi作用处沿Xi方向引起的位移。A端竖直和水平方向位移为零的条件又可以表示为

(1)

根据载荷和赘余反力X1=1和X2=1，绘制其弯矩图，如图3所示。计算得到各载荷作用下的各端点弯矩，见表1。

利用图乘法求各δ值，在图形互乘法中，基于单位载荷法求等截面杆的位移方法，得到等截面杆的线位移为

(2)

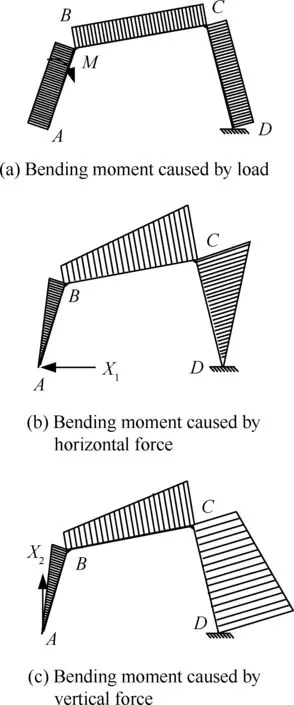
图3 柔性四杆机构弯矩图Fig.3 Bending moment of flexible four-bar linkage

表1 各载荷作用下端点弯矩Table 1 Bending moment of the end of each link

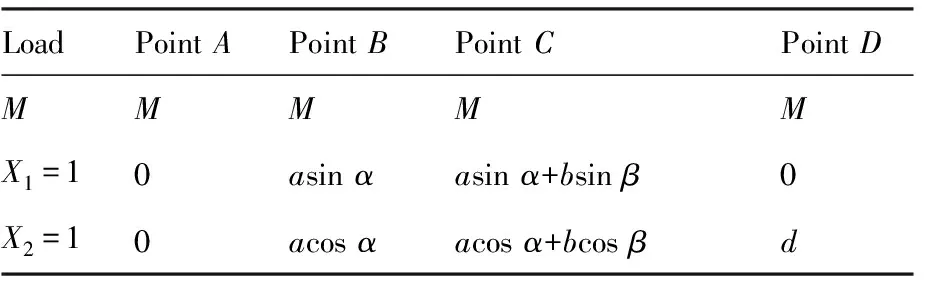
LoadPointAPointBPointCPointDMMMMMX1=10asinαasinα+bsinβ0X2=10acosαacosα+bcosβd

利用式(2)计算得到位移表达式δ1M、δ2M、δ11、δ22、δ12(见附录A)。再将各位移代入式(1)，得到端部A的支反力:

(3)

(4)

式中：Λi(i=1～13)和Vj(j=1～13)见附录A；I1、I2和I3分别为杆AB、杆BC和杆CD的惯性矩；E1、E2和E3分别为杆AB、杆BC和杆CD的弹性模量。

1.3 铰链刚度模型建立

图4 杆BC和杆CD的弯矩图Fig.4 Bending moment of link BC and link CD

由于曲柄与内圈固定，杆CD与外圈固定，因此，在力矩M作用下，B点位移反映了结构刚度。基于端点A的反力计算，得到力矩M作用下各杆件受到的弯矩，如图4所示，其中B′点为B点所在水平线与杆CD的交点，同时为杆CD杆上弯矩为零的点。将A端受力X1和X2转化到B点上，则B点受到的弯矩可以表示为

M′=M+X1asinα+X2acosα

(5)

在B点水平和竖直方向施加单位载荷，得到的弯矩分布图变化趋势与图4(b)和图4(c)一致，即当图4(b)和图4(c)中的X1=1和X2=1时的弯矩分布，得到力法正则方程中各系数(见附录A)，为了简化表达，设γ=180-φ。则B点在水平方向上和竖直方向上的位移为

{D1=D1M+D11+D12

D2=D2M+D21+D22

(6)

将B点的位移转化为AB杆的转角，进而得到含有4个四杆机构的柔性铰链的刚度为

kJ=4k=

(7)

1.4 机构最大应力点分析

根据各载荷在不同杆件上形成的弯矩进行结构中各点应力值的求解。设BC杆上的任一点离左端点B的距离为x，则BC杆上各点弯矩为

MBC=M′+(X1sinβ+X2cosβ)x

(8)

在四杆机构设计中，设置β<90°,所以BC杆上的力矩斜率大于零，而由反力分析可知弯矩MBC与反力X1、X2为异号，因此，BC杆上的最大力矩出现在B点或C点。

CD杆上的弯矩为

MCD=M′+b(X1sinβ+X2cosβ)+

x(-X1sinγ+X2cosγ)

(9)

由式(9)可得，当(-X1sinγ+X2cosγ)>0时，CD杆上的最大弯矩出现在D点，当(-X1sinγ+X2cosγ)<0时，最大值也可能在C点。因此，可能出现的最大应力为

(10)

式中：σB为杆BC的B截面的应力；σCL为杆BC右端面的应力；σCR为杆CD右端面的应力；σD为杆CD的D截面的应力；tBC为杆BC的厚度；tCD为杆CD的厚度。

2 机构优化

2.1 优化模型建立

1) 设计变量

柔性铰链的材料和几何参数决定其性能，假设柔性铰链的材料已知，即弹性模量已知。结构的整体尺寸一定，即AD杆长度和铰链厚度已知。柔性铰链的结构参数如图2所示，a和b为AB杆和BC杆的长度，α和β为AB杆和BC杆的初始水平夹角。并且设置BC杆和CD杆截面为方形，截面高度为tBC和tCD。则铰链的设计参数为X=[x1x2x3x4x5x6]=[abαβtBCtCD]。

2) 目标函数

为了得到具有较大回转角度的铰链，即需要其刚度最小，因此，目标函数为minkJ=min(4k),其中k见式(7)。

3) 约束条件

选取钛合金作为柔性铰链的材料弹性模量E=9.5×104MPa，许用应力[σ]=800 MPa，又由于铰链在转动过程中产生的应力应该在许用应力范围内，因此，考虑式(10)给出的应力值均小于[σ]。又由于考虑变截面曲梁承载特性的优势，设计BC杆截面的厚度大于CD杆截面的厚度，即得σCL<σCR，因此得

(11)

在铰链性能设计中，中心平移量不能太大，即铰链回转平面内的平移刚度需要较大，则铰链中变形杆件的截面尺寸不能太小，考虑其铰链回转刚度需满足:

kJ>100

(12)

柔性铰链的宽度为5 mm，AD杆长度d=65 mm，共同确定铰链的整体参数。AB杆与内圈固结，设其厚度为10 mm，铰链受到的力矩为M=500 N·mm。为了便于加工、安装和使用，根据经验得到其他约束条件gi(X)(i=1,2,…,9)为

(13)

2.2 优化参数选择及结果分析

由于优化模型中存在非线性的约束条件，因此考虑采用遗传优化算法进行结构尺寸优化。在利用遗传算法进行优化的过程中，种群数和遗传代数的选择对优化结果有一定的影响。为了得到全局最优解，进行了不同种群数和遗传代数对优化结果的影响分析。

由于遗传算法也具有一定的局限性，在进行非线性优化模型的优化时，可能存在优化结果的不同，因此，在初始条件和算法参数不变时，得到多个优化结果，见图5。

优化计算过程中对种群数和遗传代数的选择对优化也有一定的影响，因此，进行了算法参数的设置影响分析，见图6。

由不同参数下的优化结果可以看到，多个最优值稳定在1.34×103N·mm/rad，因此，通过遗传算法寻找到的全局最优解为1.34×103N·mm/rad。主要参数见表2。

图5 多次优化后结果Fig.5 Optimized results of many times optimization

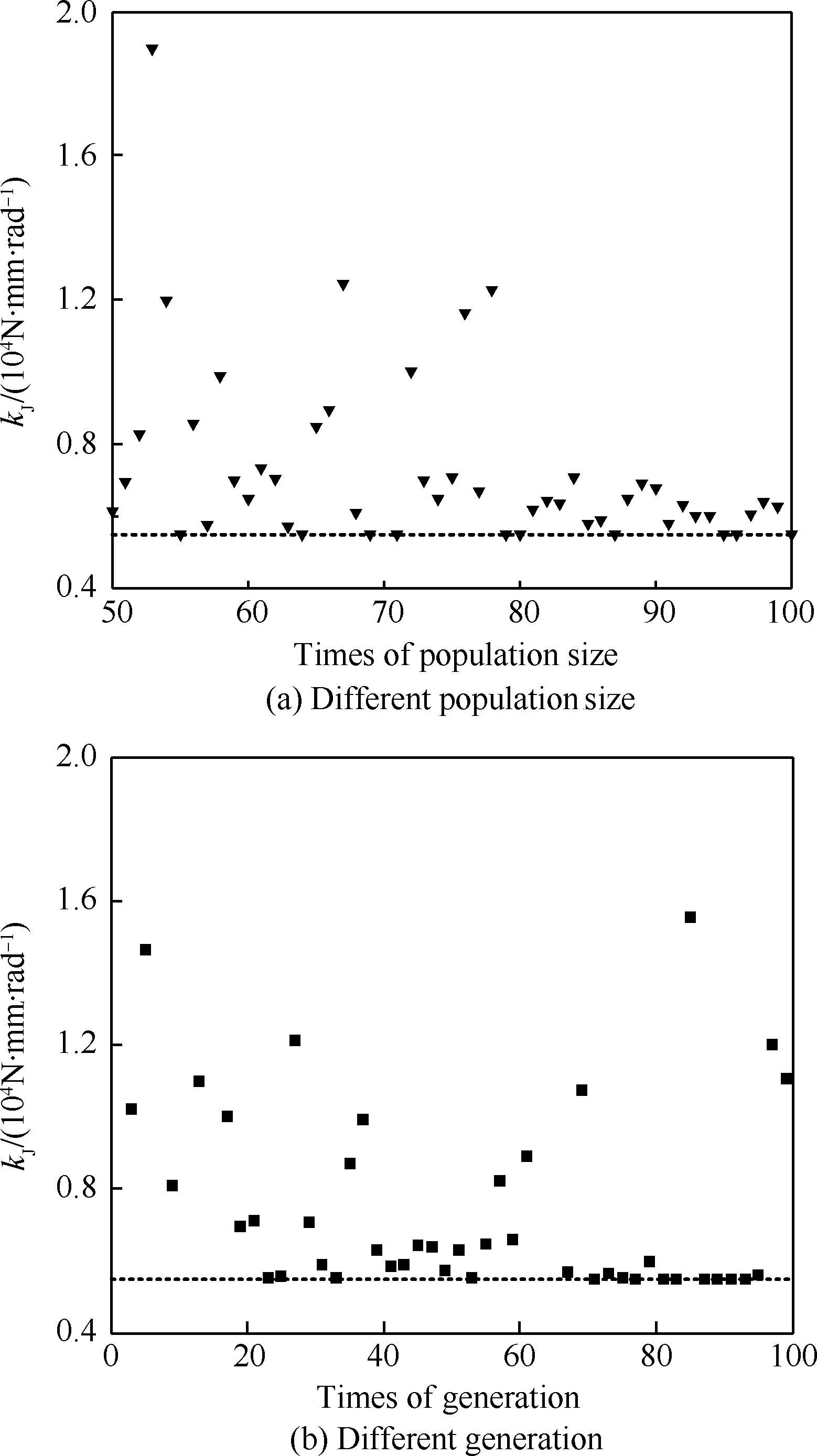
图6 不同参数设置下的优化结果Fig.6Optimized results with different parameter settings

表2 柔性铰链主要参数Table 2 Parameters of the flexible hinge

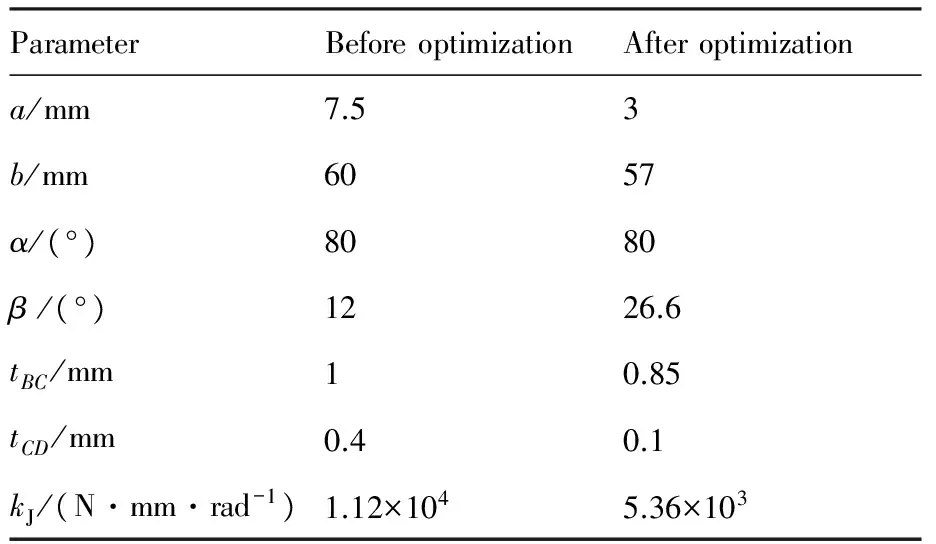
ParameterBeforeoptimizationAfteroptimizationa/mm7．53b/mm6057α/(°)8080β/(°)1226．6tBC/mm10．85tCD/mm0．40．1kJ/(N·mm·rad-1)1．12×1045．36×103

2.3 优化结果验证

由于优化模型是基于铰链刚度模型、材料性能约束和铰链的几何约束建立的，因此，通过有限元软件进行优化前和优化后的铰链模型的建立和性能分析，可以同时验证铰链刚度模型和优化模型的正确性。利用Beam188单元进行铰链有限元模型建立，其优化前后的结构参数见表2，建立的优化前后有限元模型如图7所示，两模型均包含1 924个节点和1 928个单元，且均对内圈进行全约束，在外圈的P1点和P2点施加集中力，两个模型中的集中力F分别为20 N和15 N，转化后扭矩分别为2 600 N·mm 和1 950 N·mm。通过有限元计算得到优化前后柔性铰链转过的角度为13°和20°，其变形云图如图8所示。最大应力均为779 MPa，应力云图如图9所示。通过计算得到优化前后铰链的旋转刚度分别为1.14×104N·mm/rad 和5.58×103N·mm/rad。基于理论模型得到的扭转刚度相对于有限元分析的误差分别为1.8%和3.9%。因此，有限元分析验证了刚度模型和优化结果的正确性。

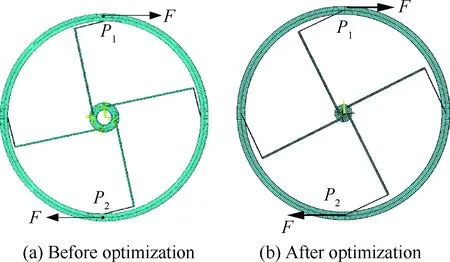
图7 柔性铰链有限元模型Fig.7 Finite element model for flexible hinge

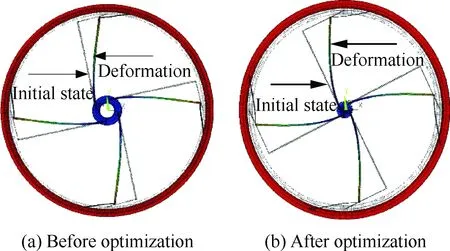
图8 柔性铰链变形云图Fig.8 Nephogram of deformation of flexible hinge

图9 柔性铰链应力云图Fig.9 Nephogram of stress of flexible hinge

在折展机构的应用中，可以基于此柔性铰链设计，通过柔性铰链的串联实现不同转角或者更大转角的转动。为了在增大转角的同时控制铰链体积，可以将被串联铰链的内外圈依次固结，从首个铰链到末尾铰链，转角不断积累，实现更大转角的转动，从而为柔性铰链在折展机构中的应用提供可靠途径。

3 结 论

1) 为了在保证柔性铰链回转刚度的前提下，提高柔性铰链的回转角度，提出了基于转角放大的四杆机构的柔性铰链设计方案。

2) 针对柔性铰链中存在的超静定问题，进行了超静定固化四杆结构的力学分析，基于固化四杆机构的力学模型，得到四杆机构的位移和应力表达式，利用几何关系的转换，得到柔性铰链的刚度模型和应力模型。

3) 建立含固化四杆机构的柔性铰链的优化模型，基于遗传算法，通过编程求解，得到了刚度为5.36×103N·mm/rad，并可以进行单向20°的回转的柔性铰链，提高了一体式柔性铰链的回转范围。

[1] 于靖军, 郝广波, 陈贵敏, 等. 柔性机构及其应用研究进展[J]. 机械工程学报, 2015, 51(13): 53-68.

YU J J, HAO G B, CHEN G M, et al. State-of-art of compliant mechanisms and their applications[J]. Journal of Mechanical Engineering, 2015, 51(13) : 53-68 (in Chinese).

[2] ZHU W L, ZHU Z W, SHI Y, et al. Design, modeling, analysis and testing of a novel piezo-actuated XY compliant mechanism for large workspace nano-positioning[J]. Smart Materials and Structures, 2016, 25(11): 115033.

[3] YANG C, YAN J H, DUKIC M, et al. Design of a high-bandwidth tripod scanner for high speed atomic force microscopy[J]. Scanning, 2016, 38(6): 889-900.

[4] 于靖军, 毕树生, 宗光华. 空间全柔性机构位置分析的刚度矩阵法[J]. 北京航空航天大学学报, 2002, 28(3): 323-326.

YU J J, BI S S, ZONG G H. Stiffness matrix method for displacement analysis of fully spatial compliant mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(3): 323-326 (in Chinese).

[5] SOYKASAP Ö, PELLEGRINO S, HOWARD P, et al. Folding large antenna tape spring[J]. Journal of Spacecraft and Rockets, 2008, 45(3): 560-567.

[6] AJI A K, HARRIS M, GARCIA D, et al. Feasibility assessment of deployable composite telescope[J]. Journal of Aerospace Engineering, 2011, 24(1): 12-19.

[7] PEI X, YU J J, ZONG G H, et al. Analysis of rotational precision for an isosceles-trapezoidal flexural pivot[J]. Journal of Mechanical Design, 2008, 130(5): 680-682.

[8] YU J J, LI S Z, SU H J, et al. Screw theory based methodology for the deterministic type synthesis of flexure mechanisms[J]. Journal of Mechanisms & Robotics, 2011, 3(3): 1194-1204.

[9] HOPKINS J B, PANAS R M. Design of flexure-based precision transmission mechanisms using screw theory[J]. Precision Engineering, 2013, 37(2): 299-307.

[10] DIBIASIO C M, HOPKINS J B. Sensitivity of freedom spaces during flexure stage design via FACT[J]. Precision Engineering, 2012, 36(3): 494-499.

[11] KIM C J, KOTA S, MOON Y M. An instant center approach toward the conceptual design of compliant mechanisms[J]. Journal of Mechanical Design, 2005, 128(3): 542-550.

[12] KIM C J, MOON Y M, KOTA S. A building block approach to the conceptual synthesis of complaint mechanisms utilizing compliance and stiffness ellipsoids[J]. Journal of Mechanical Design, 2008, 130(2): 022308-1-022308-11.

[13] REDDY B, NAIK S, SAXENA K. Systematic synthesis of large displacement contact-aided monolithic compliant mechanisms[J]. Journal of Mechanical Design, 2012, 134(1): 011007-1-011007-12.

[14] 于靖军, 裴旭, 毕树生, 等. 柔性铰链机构设计方法的研究进展[J]. 机械工程学报, 2010, 46(13): 2-13.

YU J J, PEI X, BI S S, et al. State-of-arts of design method for flexure mechanisms[J]. Journal of Mechanical Engineering, 2010, 46(13): 2-13 (in Chinese).

[15] 曹玉岩, 王志臣, 周超, 等. 考虑材料和几何构型的环形柔性铰链优化设计[J]. 机械工程学报, 2017,53(9): 46-57.

CAO Y Y, WANG Z C, ZHOU C, et al. Optimization of circular-axis flexure hinge by considering material selection and geometrical configuration simultaneously[J]. Journal of Mechanical Engineering, 2017,53(9): 46-57 (in Chinese).

[16] CIBLAK N, LIPKIN H. Design and analysis of remote center of compliance structures[J]. Journal of Robotic Systems, 2003, 20(8): 415-427.

[17] FOWLER R M, MASELLI A, PLUIMERS P, et al. Flex-16: A large-displacement monolithic compliant rotational hinge[J]. Mechanism & Machine Theory, 2014, 82(24): 203-217.

[18] YU J J, LU D F, XIE Y. Constraint design principle of large-displacement flexure systems[C]∥2014 International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), 2014: 255-260.

[19] HOPKINS J B, VERICELLA J J, HARVEY C D. Modeling and generating parallel flexure elements[J]. Precision Engineering, 2014, 38(3): 525-537.

[20] PANAS R M, HOPKINS J B. Eliminating underconstraint in double parallelogram flexure mechanisms[J]. Journal of Mechanical Design, 2014, 137(9): 092301-1-092301-9.

[21] 邱丽芳, 孟天祥, 张九俏, 等. 梳齿形柔性铰链的设计与分析[J]. 东北大学学报(自然科学版), 2014, 35(9): 1316-1320.

QIU L F, MENG T X, ZHANG J Q, et al. Design and analysis of comb-shaped flexure joint[J]. Journal of Northeastern University (Natural Science), 2014, 35(9): 1316-1320 (in Chinese).

[22] 赵山杉, 毕树生, 宗光华, 等. 基于曲线柔性单元的新型大变形柔性铰链[J]. 机械工程学报, 2009, 45(4): 8-12.

ZHAO S S, BI S S, ZONG G H, et al. New large-deflection flexure pivot based on curved flexure element[J]. Journal of Mechanical Engineering, 2009, 45(4): 8-12 (in Chinese).

Designandsizeoptimizationofflexiblehingebasedonunitoffour-linklinkage

ZHANGJing*,KOUZiming

CollegeofMechanicalEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China

Smallrotationangleandbigcenter-shiftarethemainproblemsofflexurehinges.Tosolvetheseproblems,theflexiblehingewithbigangleandhighprecisionisdesigned.Usingthecharacteristicsofangleamplificationofthecrankrockermechanismofthefour-linklinkage,thearticulatedpointsofthelinkagearefixed.Thefixedfour-barlinkageistakenasthedeformationmodule.Byusingthesmalldeformationoftherockerinthefour-linklinkage,motionoflargerotationalangleoftheflexiblehingeisrealized.Thefixedfour-barlinkageintheflexiblehingeisastaticallyindeterminatestructure.Basedonthetheoryofstaticallyindeterminatestructure,deformationandstressanalysisoftheflexibleunitisconducted.Thestiffnessmodelfortheflexurehingeisgiven.Theobjectivefunctionisderivedbasedonthestiffnessmodel,andthedesignvariablesandconstraintsaredefined.Thesizeoftheflexurehingeisoptimizedbyusingthegeneticalgorithm.AnalysisofthedeformationandstressofaspecificsizeoftheflexiblehingeusingANSYSsoftwarevalidatescorrectnessoftheoptimizationresults.

flexiblehinge;four-linklinkage;largerotationalangle;stiffness;optimization

2017-03-27；Revised2017-05-04；Accepted2017-06-12；Publishedonline2017-07-201554

URL：http://hkxb.buaa.edu.cn/CN/html/20171129.html

s：NationalNaturalScienceFoundationofChina(51505319);Special/YouthFoundationofTaiyuanUniversityofTechnology(2014TD040);QualifiedPersonnelFoundationofTaiyuanUniversityofTechnology(tyut-rc201448a)

.E-mailfree1985216@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421283

V474;TH122

A

1000-6893(2017)11-421283-10

2017-03-27；退修日期2017-05-04；录用日期2017-06-12；< class="emphasis_bold">网络出版时间

时间：2017-07-201554

http://hkxb.buaa.edu.cn/CN/html/20171129.html

国家自然科学基金(51505319)； 太原理工大学校基金(2014TD040)； 太原理工大学人才引进基金(tyut-rc201448a)

.E-mailfree1985216@163.com

张静，寇子明．基于四杆机构单元的柔性铰链设计与尺寸优化J． 航空学报,2017,38(11):421283.ZHANGJ,KOUZM.Designandsizeoptimizationofflexiblehingebasedonunitoffour-linklinkageJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):421283.

(责任编辑：李世秋)

附录A

δ21=δ12

Λ3=d+acosα+bcosβ

Λ4=3bcosβ

Λ5=3acosα

Λ6=asinα+bsinβ

Λ7=6asinα+3bsinβ

Λ8=3asinα+Λ12

Λ9=Λ13+bsinβ

Λ10=2bcosβ

Λ11=2acosα

Λ12=2bsinβ

Λ13=2asinα

V1=d+acosα+bcosβ

V2=3dcosβ

V3=3acosα

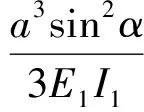
V6=2bcosβ

V7=2acosα

V8=asinα+bsinβ

V9=6asinα+3bsinβ

V10=3asinα+V12

V11=V13+bsinβ

V12=2bsinβ

V13=2asinα