一种新的多星座接收机冷启动可见星搜索算法
金春杨,范胜林,候 豆
(南京航空航天大学,南京211106)
一种新的多星座接收机冷启动可见星搜索算法
金春杨,范胜林,候 豆
(南京航空航天大学,南京211106)
为改善多星座接受机冷启动耗时过长的问题,在新的冷启动条件下,分析多星座接收机的冷启动过程,提升可见星搜索效率,并且为了能够应对复杂的遮蔽情况,提出一种新的可见星搜索算法。该算法依据已搜索的可见星缩小剩余卫星的范围,并分为4个阶段,采取不同的处理方法与搜索次序。仿真实验得出结论,在理想与遮蔽情况下,新算法均能有效缩短冷启动耗时。
多星座;冷启动;可见星搜索;搜索次序
0 引言
目前,各GNSS得到大力发展,在轨可用卫星的数量大增[1-2],多星座组合定位同步发展。多星座包括美国的GPS、俄罗斯的GLONASS、欧盟的GALIEO和中国的北斗等。较之传统的单星座定位,多星座组合定位的可用性、可靠性和精度等性能大幅提升[3-4]。但是,接收机的冷启动耗时也随卫星数量的增加而增加。
冷启动时,接收机对可见星、Doppler频移和码相位进行三维搜索[5]。通常将Doppler频移和码相位的二维搜索过程称为捕获,接收机将在这二维空间中找到一个待检测点达到有效峰值[6],并开始跟踪。已有大量文献研究如何加快捕获,例如采用硬件并行等方式[7-8]。而对于可见星的搜索,文献较少[9-10]。不论是快速的捕获,还是快速的搜索可见星,都有利于减少冷启动耗时。
传统的冷启动条件是时间、用户粗略位置、星历、历书皆未知。而实际情况下,时间与历书往往是已知并可用的,但用户粗略位置、星历未知,仍然存在三维的不确定度,称为新的冷启动条件。针对新的冷启动条件,分析多星座接收机的冷启动过程与提升可见星搜索效率的关键所在,并为应对复杂的遮蔽情况,提出一种新的可见星搜索算法。若无特别说明,后文中的冷启动均指这种新的冷启动。
1 冷启动过程
接收机冷启动的目的在于两点,一是尽快地搜索到必要数量的可见星以获得首次定位结果,二是搜索所有可见星。单星座时,两者的差异不大。但在多星座时,两者的差异十分明显,并且出于多星座接收机提高精度的初衷,后者应被更多地考虑。多星座接收机冷启动可见星搜索的大致次序可分为以下两种:
1)优先搜索到首次定位所需卫星,读取星历,首次定位,然后根据用户位置缩小可见星的搜索范围并搜索到剩余的所有可见星,读取星历,首次精确定位。
2)不依赖用户位置,直接搜索到所有可见星,读取星历,首次精确定位。
接下来以首次精确定位时间(冷启动耗时)为标准,分析比较两种次序的优劣与各自的适用情况。读取第一、第二数据块的平均耗时为24s,设单次捕获(载波频率与码相位)的平均耗时为T,多星座卫星总数为N,第一种次序平均搜索卫星总数为M1,第二种次序平均搜索卫星总数为M2,M2>M1。T与接收机的相关器数量和捕获算法有关,N与选取的星座有关,M1/N、M2/N由卫星搜索算法自身决定。由于第一种次序借助了用户位置缩小搜索范围,根据理想情况下可见星情况推测,M1/N大约为 0.4,M2/N的范围为0.4~1。 这里需要说明的是,在同一时刻,接收机采用所有硬件资源只针对同一颗卫星进行捕获的方式,而非同时对多颗卫星进行各自的捕获,以尽可能缩短T。当然,捕获到某颗卫星的某个频点后,某个通道就被专门用于跟踪此卫星的此频点,不再参与对其他卫星的捕获。因为这种串行的搜索方式才能够运用已有的搜索结果辅助决定之后的搜索次序,以避免不必要的搜索,而并行的搜索方式却使得各自的搜索结果是独立的并且无法相互辅助。可见星搜索算法的目的正是要给出串行搜索的最优次序。
忽略定位解算等其他耗时,由于有两次不重叠的读取星历的过程,第一种次序的冷启动耗时为:
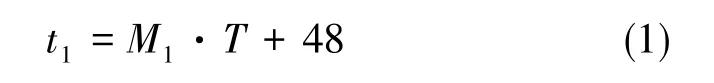
第二种次序的冷启动耗时为:

两者之差为:
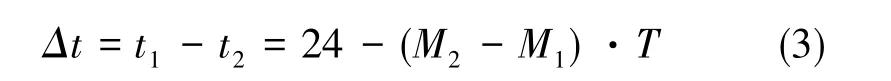
式(3)中,第一项24反映读取第一、第二数据块的耗时,第二项(M2-M1)·T(必大于0)反映搜索耗时的差异。可以看出,如果读星历的耗时比重越大,则越应考虑使用第二种次序。不论采用第一种还是第二种次序,为缩短冷启动耗时,都可以采用减小T的方式。而在(M2-M1)固定的情况下,随着T的减小,Δt将变大,也就是更可能采用第二种次序。并且如果可以设计特定的算法使得M2更加接近M1,不但减小t2,也会使得Δt变大,同样更可能采用第二种次序。在第二种次序的基础上,提出一种新的卫星搜索算法。因此,新算法的适用条件是:Δt>0。
2 一种新的可见星搜索算法
文献[9]提出了一种动态可见星搜索算法,在理想无遮蔽的情况下可有效减少冷启动耗时。该算法引入平均可见度的概念,某颗卫星的平均可见度由自身位置与备选用户粗略位置的集合共同决定,优先搜索平均可见度最大的卫星。该算法本身不能区分卫星不可见是由于地球遮蔽或是物体遮蔽,所以在实际有遮蔽情况下,极易退化为全星搜索。为解决这一问题,文献[10]提出了一种鲁棒动态可见星搜索算法。该算法在平均可见度的基础上,引入遮蔽概率和置信度的概念,在一定程度上解决实际有遮蔽情况下算法退化的问题,但是并未给出详实的遮蔽情况分析与仿真验证。本节提出一种新的可见星搜索算法,新算法假设t和历书由外部给定,并不再如同文献[9]和文献[10]中简单地给出可见度估计准则、并按降序搜索,而是将冷启动分为4个不同的阶段。第一阶段搜索初始卫星组,第二阶段搜索边缘卫星组,第三阶段外延、内缩搜索,第四阶段搜索剩余卫星,每个阶段按照不同的准则确定搜索次序。
2.1 可见星搜索算法原理
可见星搜索算法能够降低冷启动耗时的实质是避免搜索理论已不可见的卫星,即缩小剩余卫星的可能范围,算法的效率主要由搜索次序与实际情况决定。从这个角度来说,文献[9]和文献[10]的问题在于过度地压缩剩余卫星的范围,从而退化为全星搜索,新算法将快速、合理地给出剩余卫星的最小范围。
在冷启动过程中,某一颗卫星是否被遮蔽是无法判断的。而文献[9]将不可见的搜索结果全部判断为地球遮挡,文献[10]的算法引入遮蔽概率与置信度的概念,但是仍然不能彻底排除误判的可能。为应对各种复杂的遮蔽情况,新算法将不再根据不可见的搜索结果对剩余卫星做剔除,只根据搜得的可见星做处理,从而排除误判的可能。这使得算法对于遮蔽情况具有极强的鲁棒性,但是同时会损失一定的效率。为弥补这部分的效率损失,也为提高整体的效率,需要设计特定的搜索次序以提升效率。
提升搜索效率的关键,首先在于尽快地搜索到第一颗可见星,为此设计第一阶段;其次在于快速地确定最外围的可见星,为此设计第二阶段和第三阶段。需要说明的是,搜索到第一颗可见星之后,按照一般的思路会搜索其附近的卫星,但这不利于缩小剩余卫星的范围,因为越接近的卫星,对于缩小剩余卫星范围的作用越是重叠。并且,当遮蔽情况较为复杂时,可见星附近的卫星未必是可见的。另外,由于只根据可见的搜索结果缩小剩余卫星的范围,那么,最外围的可见星就确定了剩余卫星的最小范围,尽快确定最外围的可见星,也就是尽快缩小剩余卫星的范围。
在提出4个阶段之前,先说明算法如何根据一颗可见星剔除理论不可见的卫星:设某颗可见星为SV1,另一颗待检验卫星为SV2,已知两者在ECEF中瞬时坐标,选取过SV1、SV2和地心3个点的截面,如图1所示。
图1中,r表示地球平均半径,h1、h2分别表示SV1、SV2距地心瞬时高度,α表示接收卫星信号最小仰角,β表示假设临界情况时SV1与SV2的夹角,βreal表示实际夹角。β由式(4)得出:
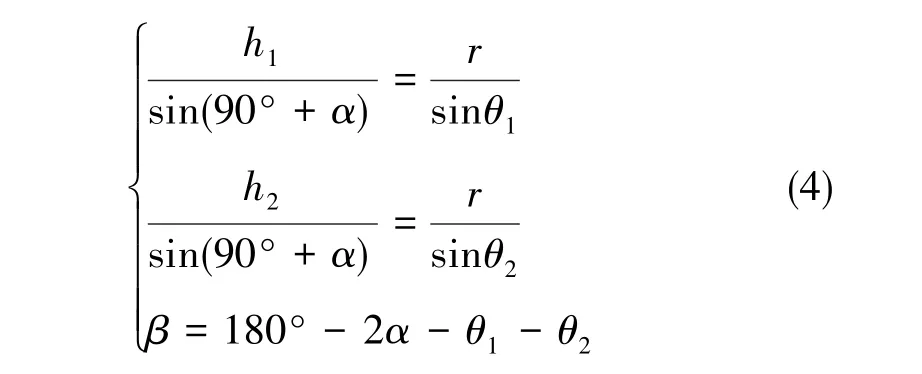

图1 剔除理论不可见星Fig.1 Rejecting theoretically invisible stars
如果βreal>β,则SV2理论已不可见。
在此基础上,提出以下4个阶段。
第一阶段为搜索初始卫星组,初始卫星组的构造方法基于以下前提:
1)理想情况下,以地心为体心,大致构成正四面体的4颗卫星。更准确地说,是地心到卫星连线之间的角度关系与正四面体体心到顶点连线之间的角度关系相一致的4颗卫星,其中必有一颗可见,并可以自然地推广到正六面体、正八面体等。
2)当一颗卫星不可见时,其他卫星的(地心到卫星)向量与该卫星的夹角越小,则受遮蔽的可能性就越大。
初始卫星组的构造方法如下:首先根据前提1找到4颗卫星,它们在ECEF中的空间向量分别与以下 4 个空间向量(1,1,1)、(1,-1,-1)、(-1,1,-1)、(-1,-1,1)的夹角最小,理想无遮蔽情况下,其中必有一颗可见。需要说明的是,这组空间向量只是符合正四面体角度关系的一例,也可以选择另一组空间向量,只要满足角度关系即可。如果这4颗卫星都不可见,说明这4个方向受到遮蔽,根据前提2,之后选取的空间向量应尽可能避之。并结合前提1,按照以下4个空间向量(-1,-1,-1)、(-1,1,1)、(1,- 1,-1)、(1,1,-1),搜索新的4颗卫星。如果仍都不可见,则按以下 6 个空间向量搜索(1,0,0)、(0,1,0)、(0,0,1)、(-1,0,0)、(0,- 1,0)、(0,0,-1)。以此类推,新的空间向量尽可能避开旧的空间向量,并使用必要的数量以保证理想情况下必有一颗可见。在对这些卫星搜索的过程中,一旦有某颗星可见,则退出第一阶段,进入第二阶段。
第二阶段为搜索边缘卫星组,边缘卫星组的构造方法如下:
设第一颗可见星的星下点为位置P,选取在P当地坐标系中的仰角处于一个特殊范围内的卫星,作为边缘卫星组。这个范围的下限是接受卫星信号的最小仰角,上限是在最小仰角基础上加20°(仅作举例,可适当调整)。设仰角下限为α1,上限为α2,待检验卫星距地心高度为h,地球平均半径为r,第一颗可见星为SV1,待检验卫星为SV2,βreal表示实际夹角,如何确定SV2是否属于边缘卫星组,如图2所示。
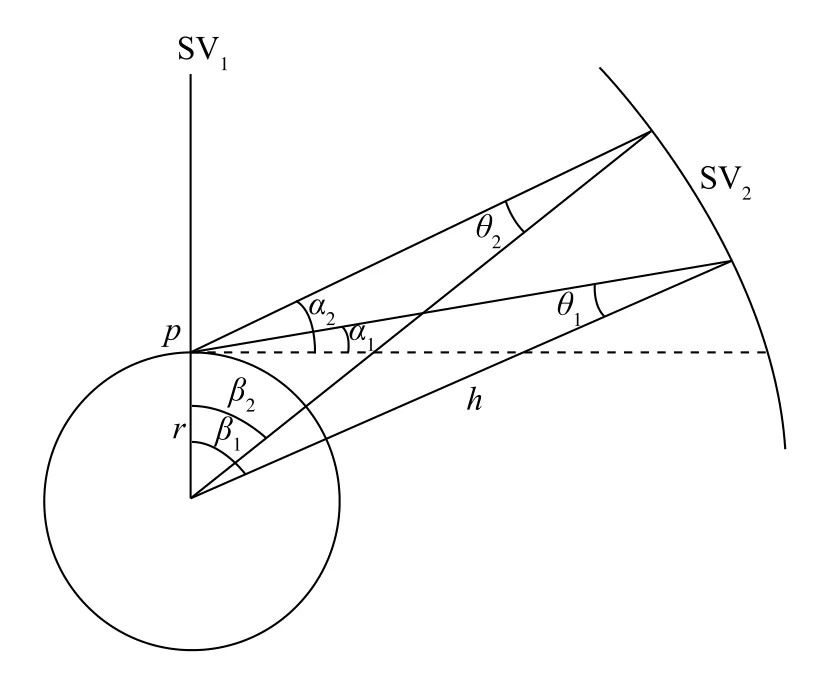
图2 构建边缘卫星组Fig.2 Constructing the group of edge stars
图2中,β1、β2分别表示SV1与SV2的夹角上限与下限,由式(5)得出:

如果β2<βreal<β1,则SV2进入边缘卫星组。
第三阶段为外延、内缩搜索。在第二阶段的基础上,如果某颗边缘卫星可见,该卫星将大幅地缩小剩余卫星的范围。为进一步缩小剩余卫星的范围,则应沿着第一颗可见星到该卫星的连线方向,搜索更外围的卫星,直到搜索结果为不可见,这是外延搜索;如果某颗边缘卫星不可见,该卫星并不能缩小剩余卫星的范围,为找到其附近的可见星,则应沿着该卫星到第一颗可见星的连线方向,搜索更内部的卫星,直到搜索结果为可见,这是内缩搜索。为尽快缩小剩余卫星范围,显然,应先进行外延搜索,再进行内缩搜索。
第四阶段为搜索最后剩余的卫星,在此阶段的搜索次序已不再重要,需要做的就是把剩余卫星逐个搜索,可按任意次序。
总之,算法在第一阶段快速搜索到第一颗可见星,在第二、三阶段搜索卫星并快速确定剩余卫星的合理的最小范围,在第四阶段搜索最后剩余的卫星。
2.2 算法流程
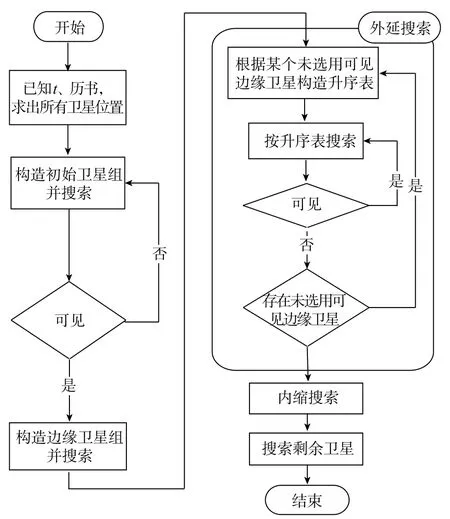
图3 算法流程图Fig.3 Flowchart of algorithm
图3为算法流程图。其中,剩余理论仍可见卫星的更新没有直接给出,初始搜索卫星组的具体细节与升序表的构造见2.1节。图中有所省略,内缩搜索可由外延搜索类推,没有重复给出。
3 仿真验证
算法由Matlab仿真验证,共有的仿真条件如下:1)星座由GPS、GLONASS、GALIEO、BEIDOU组成,共93颗卫星;2)TLE文件由www.celestrack.com获得,获取时间为2016年10月12日;3)用户位置设定为南京(32.05°N,118.78°E); 4)仿真时间的日期设定为2016年第300天(UTC)。
在共有的仿真条件之上,分4种遮蔽情况:1)理想无遮蔽;2)低仰角遮蔽,在用户坐标系中的仰角低于30°的卫星不可见;3)单壁遮蔽,在用户坐标系中x坐标大于107m的卫星不可见;4)峡谷遮蔽,在用户坐标系中x坐标在(-107m,107m)区间之外的卫星不可见。
对于每种遮蔽情况,分别选取仿真日期当天的24个整点进行仿真验证,结果如图4所示。
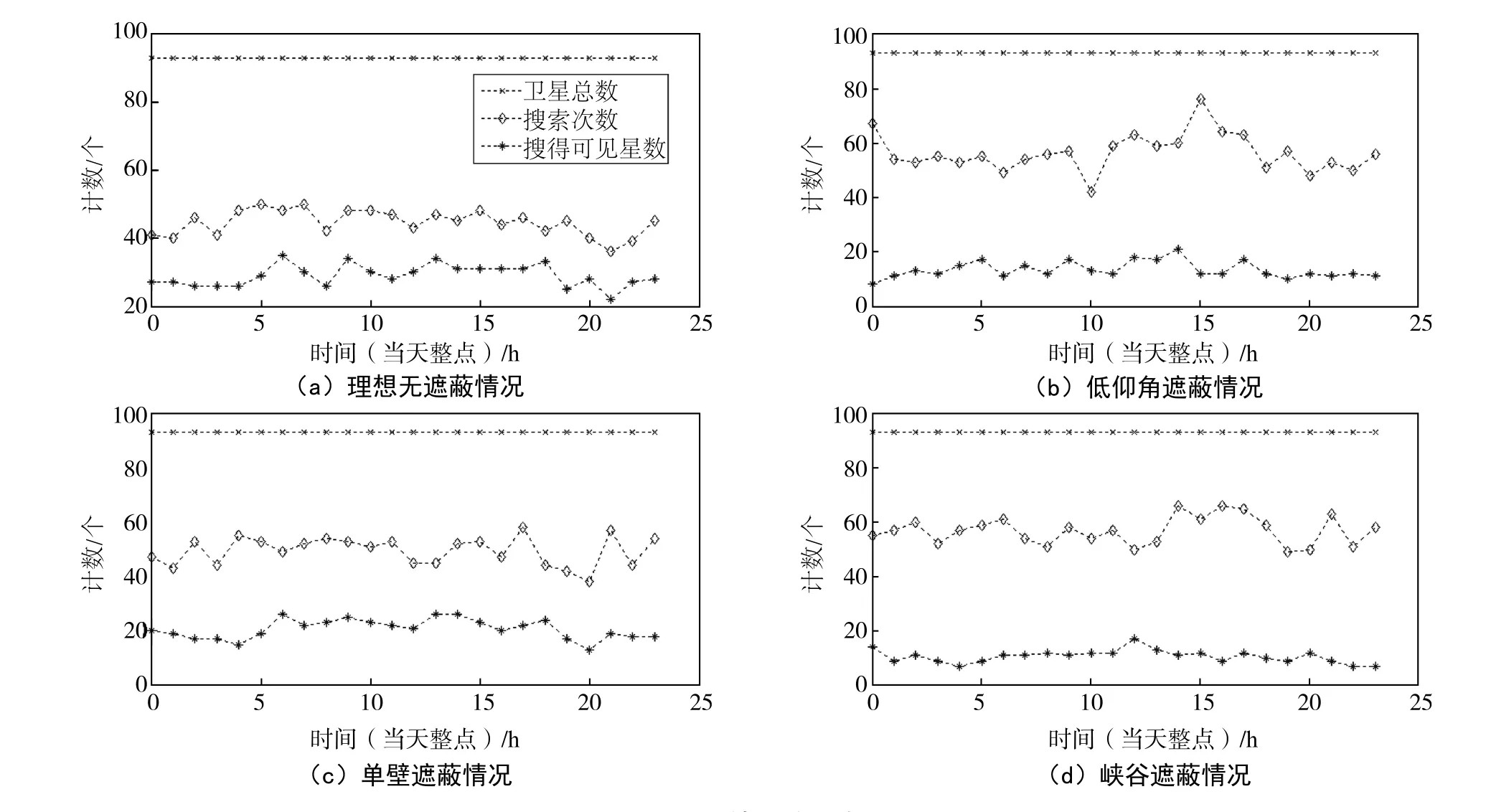
图4 4种情况的仿真结果Fig.4 Simulation results of 4 situations
由图4可以看出,随着整点时间变化,算法的搜索次数存在一定范围的波动,但保持稳定。4种遮蔽情况下,可见星数量不同,算法的效率也有所差异,但搜索次数都明显小于卫星总数,都能够有效减少冷启动耗时。
4种情况下算法的性能如表1所示。

表1 4种情况下算法的性能Table 1 Algorithm performance of 4 situations
4 结论
在多星座的背景下,为尽可能地减少冷启动耗时,并应对复杂的遮蔽情况,提出一种新的卫星搜索算法。算法只根据可见的搜索结果缩小剩余卫星的范围,并通过第一阶段快速地搜索到第一颗可见星,进而通过第二、三阶段快速地获得剩余卫星合理的最小范围。因此,算法对于遮蔽情况具有极强的鲁棒性,并保持高效。较之文献[9]和文献[10],算法为多星座接收机提供更鲁棒、更高效的冷启动方案。接下来将进一步研究,在遮蔽较为严重的情况下,如何保持并提高可见星的搜索效率。
[1]Davis L A,Enge P K,Gao G X.Global navigation satellite systems[M].Washington D.C:National Academic Press, 2012.
[2]Hofmann-Wellenhof B,Lichtenegger H,Wasle E.GNSS-global navigation satellite systems: GPS,GLONASS,Galileo,and more[M].New York: Springer,2007.
[3]Huang B,Yao Z,Guo F,et al.STARx-a GPU based multi-system full-band real-time GNSS software receiver[C].ION GNSS,2013: 1549-1559.
[4]Joerger M,Neale J,Pervan B,et al.Measurement error models and fault-detection algorithms for multi-constellation navigation systems[C].Position Location and Navigation Symposium,2010: 927-946.
[5]Rycroft M J.Understanding GPS:principles and application[J].Journal of Atmospheric and Solar-Terrestrial Physics,1997,59(5): 598-599.
[6]Misra P,Enge P.Global positioning system: signals,measurements,and performance[M].Lincoln: Ganga-Jamuna Press,2011.
[7]Lin D M,Tsui J B Y.Acquisition schemes for SofWare GPS receiver[C].Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation,1985: 317-325.
[8]Van Nee D J R,Coenen A J R M.New fast GPS code-acquisition technique using FFT[J].Electronics Letters,1991,27(2): 158-160.
[9]Chen K T.A dynamic satellite search scheduling for GNSS super constellation[C].Proceedings of the 21stInternational Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS,2008.
[10]Zhou H,Yao Z,Lu M.A robust dynamic satellitesearching algorithm for multi-constellation GNSS receivers[M].Berlin: Springer-Verlag,2015.
A New Visible⁃star⁃searching Algorithm for the Cold⁃start of the Multi⁃constellation Receiver
JIN Chun-yang,FAN Sheng-lin,HOU Dou
(Nanjing University of Aeronautics and Astronautics,Nanjing 211106)
Analyse the cold-start process of the multi-constellation receiver and the key to enhance the efficiency of the visible-star-searching to reduce the cold-start time of the multi-constellation receiver under the new cold-start condition.In addition,a new visible-star-searching algorithm is proposed to solve the complex masking problem.The algorithm narrows the scope of the remaining satellites only according to visible-stars which have been acquired,and is divided into four sections with different processing methods and searching sequences.The simulation experiment is conducted and the conclusion is that the new algorithm is captive to reduce the cold-start time whenever the situation is ideal or with the masking problem.
multi-constellation receiver; cold-start; visible-star-searching; searching sequence
P228.4
A
1674-5558(2017)01-01384
10.3969/j.issn.1674-5558.2017.06.005
2017-04-06
金春杨,男,硕士,导航、制导与控制专业,研究方向为多星座组合定位。

