MEMS环形谐振陀螺闭环系统建模、仿真与参数分析

王 浩，叶泽刚，张奇荣，权海洋

（北京微电子技术研究所，北京100076）

MEMS环形谐振陀螺闭环系统建模、仿真与参数分析

王 浩，叶泽刚，张奇荣，权海洋

（北京微电子技术研究所，北京100076）

针对一款数字可配置的MEMS环形谐振陀螺，对陀螺表头和信号处理电路进行数学建模，推导陀螺检测系统指标参数与机电特性参数之间数学关系，为可配置ASIC电路提供理论支撑。通过对实测表头数据和理论模型数据进行对比分析，验证了模型的有效性与准确性。

MEMS；环形谐振陀螺；系统建模；数字可配置

0 引言

一款基于柯氏力效应的MEMS环形谐振陀螺BVSG01，其敏感结构如图1所示。MEMS环形谐振陀螺包括MEMS结构和ASIC控制电路，该陀螺可根据应用需求对陀螺带宽、量程等参数进行数字化配置。

BVSG01表头直径仅4mm，采用圆片级真空封装，设计了ASIC专用处理电路进行信号处理与角速率检测。陀螺表头与检测ASIC电路实现了SIP集成封装，封装后尺寸仅 16.7mm×11.6mm×4.5mm，如图2所示。其中，ASIC处理电路是一款数字可调ASIC检测电路，可通过OTP（One Time Program）进行电路参数的再配置，包括电路增益、滤波器带宽等，从而可对陀螺闭环性能、检测指标进行调整。同时，可对片上微处理器MCU进行程序修改，调整闭环控制器的结构或参数，也可调整陀螺检测系统参数。

本文对MEMS环形陀螺进行了表头、电路、闭环控制程序等机电一体化建模，得到陀螺检测Simulink系统的理论模型。通过仿真与理论计算分析，建立陀螺系统指标（带宽、标度因子、零偏稳定性等）与陀螺表头参数、电路配置参数的数学关系，为陀螺参数配置提供理论支撑，可根据实际应用需求对陀螺参数进行配置。

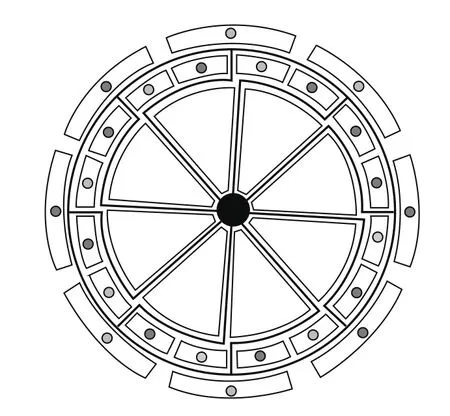
图1 MEMS环形谐振陀螺结构示意图Fig.1 Architecture of MEMS vibrating ring gyroscope

图2 MEMS环形陀螺Fig.2 MEMS vibrating ring gyroscope

1 陀螺闭环模型建立

1.1 闭环检测系统结构分析

MEMS环形陀螺采用闭环检测，闭环控制系统包括驱动模态控制、敏感模态控制。驱动模态闭环控制包括PLL（锁相环）环路与AGC（自动增益控制）环路，分别实现陀螺自然谐振频率的跟踪与驱动模态的振幅稳定。敏感模态也包括两个闭环回路，力平衡回路与正交抵消回路：力平衡回路通过反馈控制，施加与柯氏力相反的静电力，使敏感模态保持平衡位置，该反馈静电力的大小则表征角速率大小；正交抵消回路则是通过静电反馈力的形式，消除由驱动模态耦合引起的敏感模态振动。

闭环检测的优点是：通过负反馈控制方式，使角速率闭环检测可以提高标度因子线性度；同时，力反馈模式下敏感模态位移很小，避免了敏感模态振动对驱动模态的耦合扰动；角速率检测带宽则根据闭环控制器进行调整。因此，采用闭环控制的MEMS陀螺具有更高的精度。

基于环形陀螺与检测ASIC电路的闭环系统架构如图3所示，最左边为机械表头结构。表头结构产生的位移信号通过电容式微小信号C-V检测电路进行信号检测，然后信号自AD电路转化为数字信号，通过数字专用ASIC电路对两个模态的信号分别进行处理，并通过反馈回路施加到两个模态的驱动端。

1.2 环路主要单元模块数学模型建立

陀螺检测系统的4个闭环回路的信号处理方式相似，由于力平衡环路负责角速率检测与输出对陀螺系统参数有直接影响，因此，通过对力平衡环路进行分析，介绍闭环建模的方法。

力反馈环路从陀螺表头检测端到表头驱动端，信号经历的主要环节包括：C-V小信号检测、前端信号放大与滤波、进入ADC实现数字化、信号解调、反馈控制器、DAC数字信号转模拟信号、驱动端静电力，信号处理如图4所示。

（1）陀螺表头模型

MEMS陀螺微机械结构可等效为 “质量—阻尼—弹簧”的2阶系统，其传递函数为：

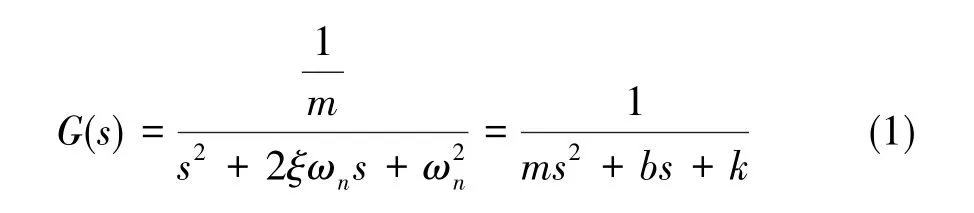
其中，m为参与振动的有效质量，b为阻尼率，k为谐振器等效刚度，ωn为自然谐振频率，ξ为阻尼系数，

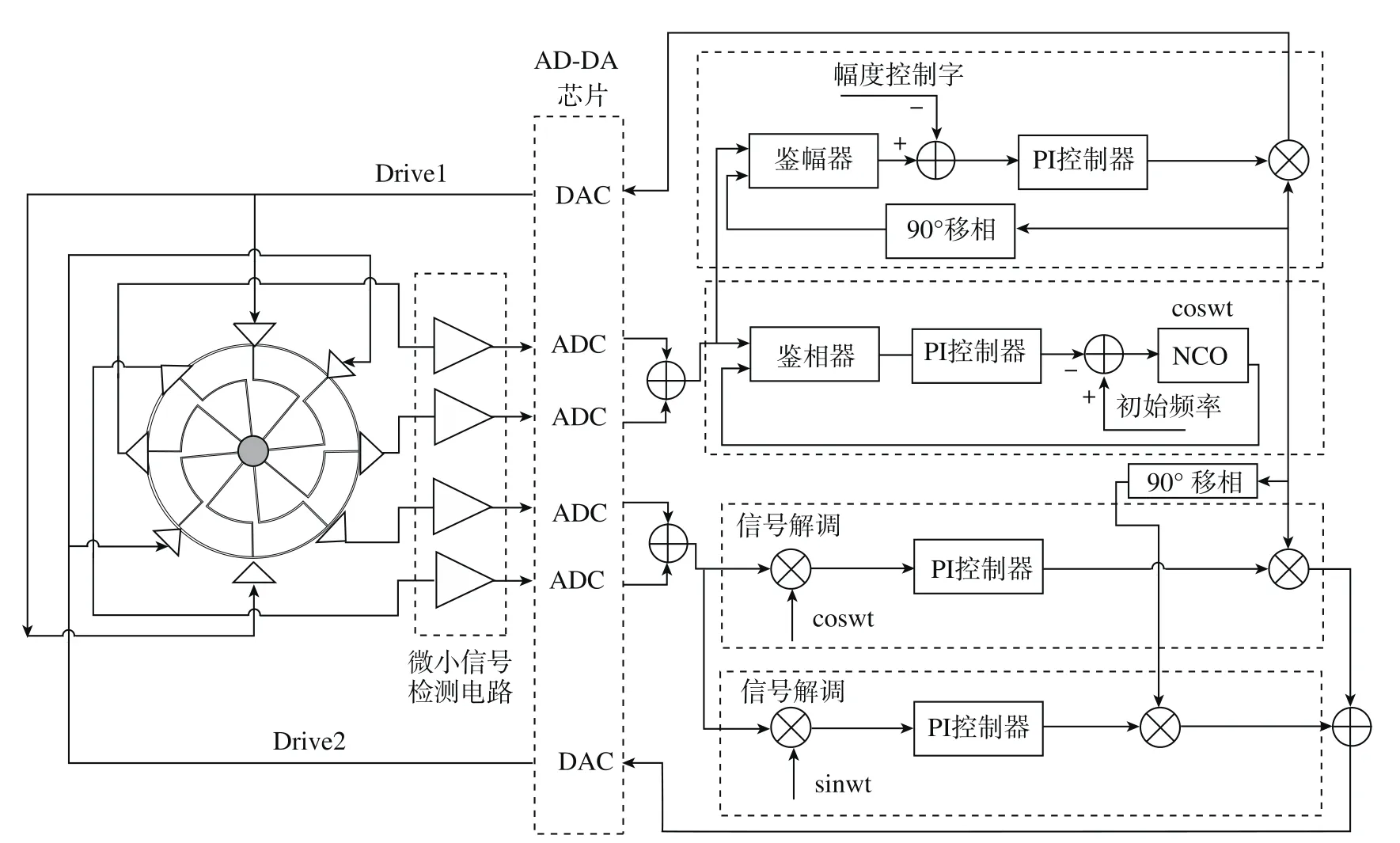
图3 MEMS陀螺全闭环检测系统结构示意图Fig.3 Block diagram of MEMS gyroscope close-loop detecting system

图4 力平衡环路信号处理框图Fig.4 Frame of rebalance loop signal processing

（2）柯氏力增益

角速率转为柯氏力的增益为：

其中，Ag为环形陀螺的角度增益，A1为敏感模态的振动位移幅度。

（3）C-V 转换电路

陀螺机械结构位移经过C-V转换电路，将振动位移信号转化为电信号。该C-V电路是一块低噪声运放（LNA）分析电路，其数学传递函数为：

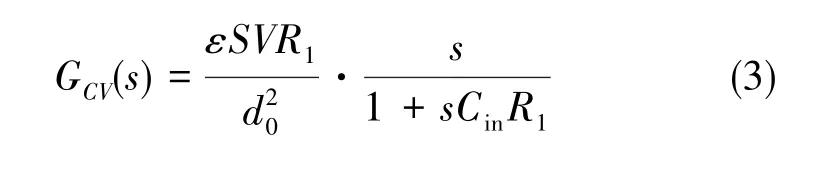
（4）带通滤波器

带通滤波器的功能是传递有效角速率信号，同时对微结构的机械布朗噪声以及前端电路噪声进行抑制。通过对电路进行分析，带通滤波传递函数为：

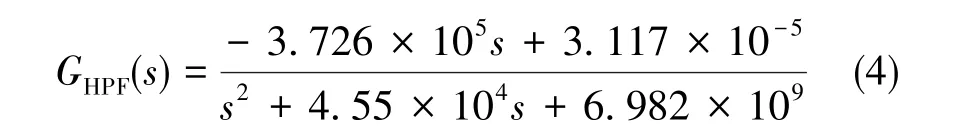
（5）环路控制器

环路控制通过微处理器程序实现，是可配置模块。最简单的控制器为一个常数，通常情况为了调整带宽、降低噪声影响，优化环路特性，环路控制器采用滤波器或PI控制器，控制器形式如下：

环路控制器是闭环设计的重点，它影响着闭环系统的稳定性、带宽、环路噪声、幅度裕度、相位裕度、跟踪速度等特性。

（6）力电转换

当闭环驱动电压施加到驱动电极时，会产生静电驱动力到质量块。该静电力不仅与驱动电压有关，同时与可动质量块直流偏置、静电电极的面积、电极与可动质量块的距离等要素有关系。推导得静电电压到静电力的增益为：

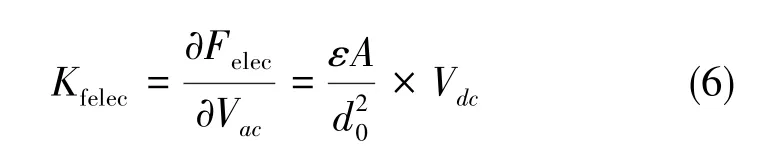
（7）其他模块

ADC/DAC等效为增益项，主要与有效位数有关：

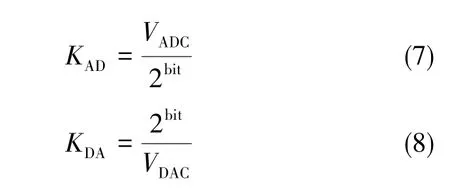
其中，VADC是ADC的最大输入电压，VDAC是DAC输出的最大电压，bit为 ADC/DAC的有效位数。

幅度解调模块的增益项用Kamplitude表示。

1.3 Simulink闭环模型建立

对陀螺全闭环检测系统进行Simulink建模，如图5所示。该模型包含了陀螺实际信号流中每一个单元模块的数学模型，该模型可以准确地反映陀螺闭环系统的信号传递与数据处理。基于该模型的仿真或计算，可以有效分析信号传递与处理路径的每一个单元模块的参数对陀螺检测系统的性能参数的影响。

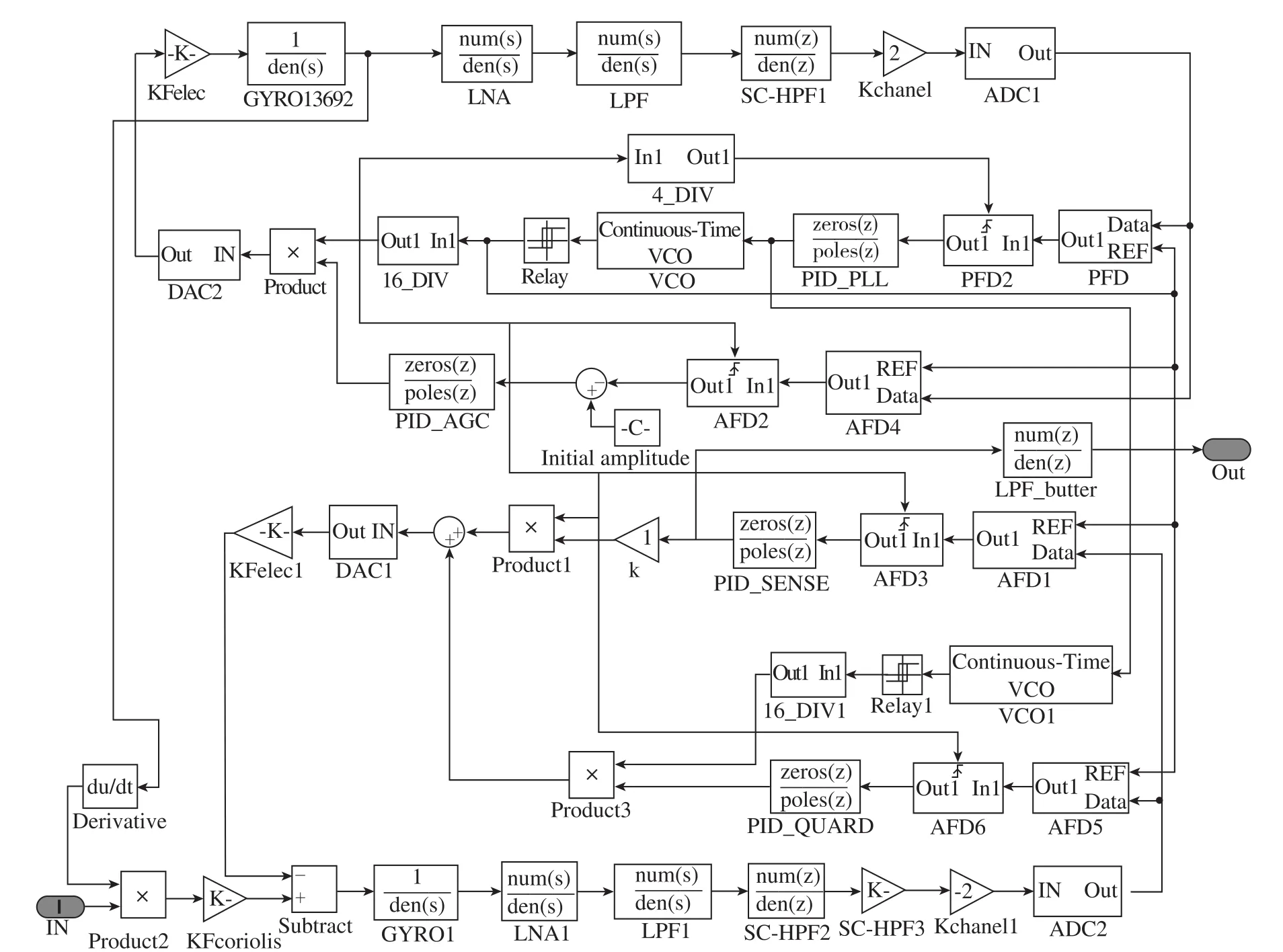
图5 MEMS陀螺检测系统Simulink模型Fig.5 Simulink model of MEMS gyroscope system

2 理论模型等效与指标分析

Simulink模型是对陀螺机电系统进行一一对应的模拟等效，可以通过模型仿真得到很多检测系统的特性，但是该模型存在非线性单元，无法直接采用数学分析、经典控制理论等方法进行参数分析与设计。因此，需对该模型进行深入的等效、简化，得到线性的闭环控制系统模型。

2.1 陀螺表头等效计算

陀螺闭环系统并不是直接对陀螺的2阶系统进行控制，而是对 “调制—陀螺2阶系统—解调（鉴相/鉴幅）”模块进行闭环控制，如图6所示。

当存在角速率输入Ω时，根据科氏力表达式知：角速率Ω被高频谐振频率的ωn载波信号进行调制。假设角速率输入信号是正弦信号Ω＝Asinω0t，其中，ω0＜＜ωn，科氏力增益为Kcoriolis。则A点信号为：XA＝KcoriolisAsinω0t。经过调制后，在B点的信号为频率成分为（ωn＋ω0）与（ωn－ω0），如图7所示。

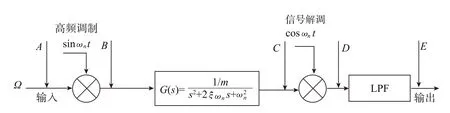
图6 调制—陀螺2阶系统—解调模块Fig.6 Module of modulation-gyroscope second order system-demodulation

图7 信号传递的频率变换Fig.7 Frequency change in signal transfer process

B点信号经陀螺机械表头，到达C点的信号频率成分仍然为（ωn＋ω0）与（ωn－ω0）。从C点到D点，信号经高频载波信号cosω0t进行解调。解调后信号的低频成分频率为ω0，高频成分被低通滤波器滤掉，到E点后信号频率成分仅剩下ω0。根据定义，信号由A点传递到E点的直流增益为：。

陀螺2阶传递函数的微分方程的解为：y＝。其中，C1e－ξωnt表示直流增益，计算得；θ为信号经过陀螺表头后产生的相移。根据定义，该解为陀螺的阶跃信号响应。最终在E点为低频或直流信号，则E点的阶跃响应为去除高频成分的信号，即yE＝C1e－ξωnt，该表达式即为阶跃输入信号的增益。对其进行 Laplace变换，得到。又有。

经计算得，调制—2阶系统—解调的陀螺系统可等效为1阶传递函数：

2.2 闭环理想模型简化

角速率信号经过柯氏力增益后被调制到高频信号，信号经过陀螺表头、C-V电路、运放与滤波器，其有效信号频率均在陀螺自然谐振频率左右。为方便分析，分别用C-V电路、滤波器在谐振频率点的增益项代替其传递函数：

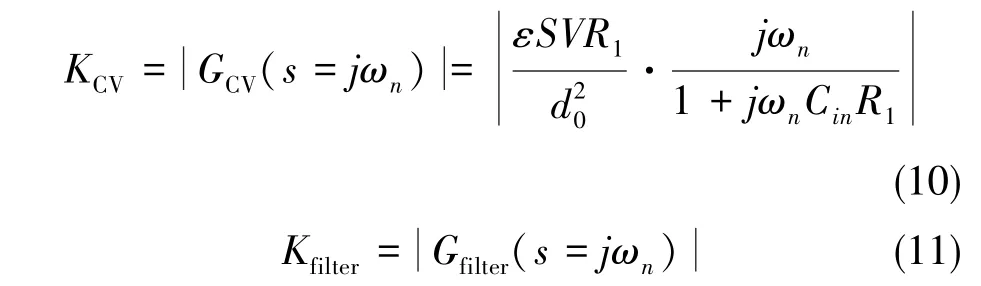
则可得到简化的线性闭环模型，如图8所示。

图8 简化的理想闭环回路Fig.8 Simplified ideal closed loop

2.3 陀螺检测系统参数计算

根据简化的线性闭环模型，可以通过计算、分析得到陀螺检测系统的重要参数。

（1）带宽

陀螺检测系统可进一步简化为图9所示的形式，计算得到陀螺闭环检测系统传递函数为：

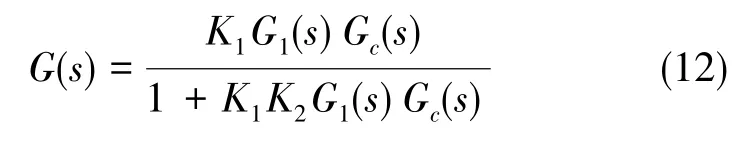
其中，K1＝KCV·Kfilter·KADC·Kamplitude，K2＝KDAC·KFelec。G1（s）代表陀螺表头传递函数，GC（s）为闭环PI控制器的传递函数。K1、K2可通过OTP电路进行配置、调整，GC（s）闭环控制器可通过修改程序实现调整，因此陀螺检测系统可实现数字化配置，调整闭环传递函数，进而调整陀螺检测带宽。

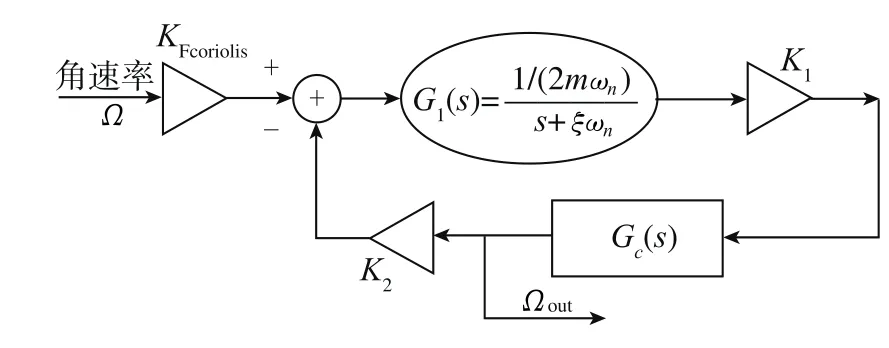
图9 最简的闭环系统Fig.9 Most simplified closed system

（2）标度因子

科氏力为Fc，反馈静电力为Felec，角速率到科氏力增益为Fcoril，驱动电压到静电力增益为kelec。根据闭环反馈的性质，有Fc＝Felec，则：Ωout·kDAC·kelec＝Ω·kcoril，计算标度因子得：

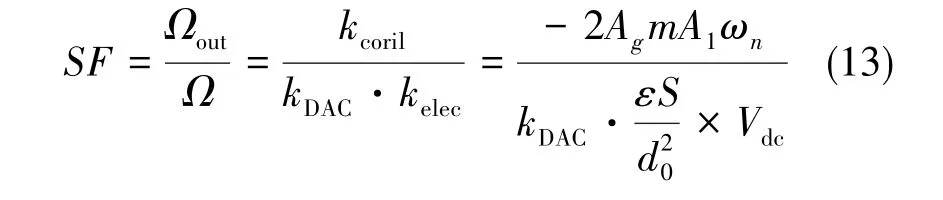
（3）分辨率

分辨率是指陀螺检测到的最小角速率增量。对于数字化陀螺，分辨率主要由模数转换电路（ADC）的分辨率决定。角速率信号传递到ADC时，必须大于ADC的分辨率，即：

其中，V为ADC电源电压，bit为ADC有效位数。计算得陀螺能分辨的最小角速率为：

（4）量程

根据分析，柯氏力与静电反馈力近似相等，即Fc≈Felec。静电反馈力的上限受静电最大电压限制，即，则有：

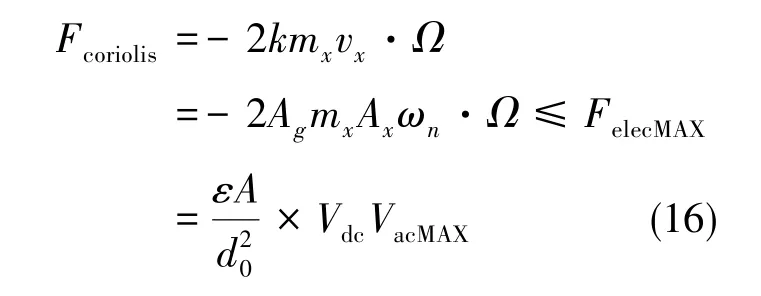
可计算得到陀螺能检测到的最大角速率值，即量程为：

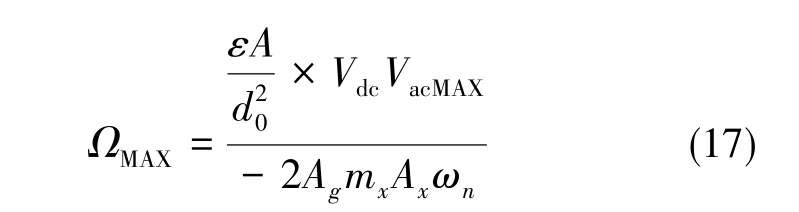
其中，VacMAX是反馈驱动电压的上限值。根据公式，量程可由第一模态振动位移Ax进行调节，Ax可由OTP电路调节。

（5）零偏稳定性

零偏稳定性的计算公式为：BS＝。其中，Fi是每次采样的时域角速率值，是角速率的零位偏移平均值，K为标度因子。可见陀螺零偏稳定性是在零角速率输入的情况下，噪声传递到角速率输出端的表征。如图10所示，设NA代表陀螺机械噪声，单位为代表前端 C-V电路噪声，单位为则A点噪声传递到输出端的噪声为NAout＝NA·G1（s）K1GC（s）； 同理，由B点传递到输出端的噪声为NBout＝NB·K1GC（s）。

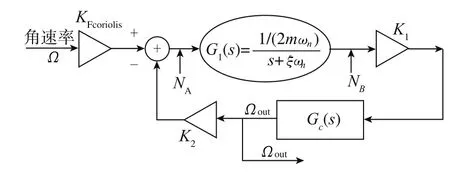
图10 带噪声模型的简化闭环系统Fig.10 Simplifyed closed system with noise model

闭环回路中还有其他噪声源传递到角速率输出端。最终，输出端的噪声为：

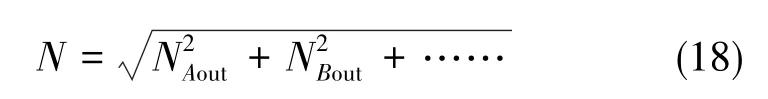
陀螺零偏稳定性由两个因素决定：1）陀螺闭环检测系统中的噪声源大小；2）信号处理路径对噪声的抑制能力。

信号带宽与噪声带宽通常差别很大，闭环系统中的环路滤波器、闭环控制器等对噪声都有一定带宽限制作用，因此可以通过巧妙地配置电路参数与控制器参数，对噪声进行最大的抑制，提高陀螺零偏稳定性。

3 模型仿真与测试结果分析

3.1 系统幅频特性

验证系统建模是否准确，最主要的方法是检验理论模型的系统响应与陀螺实际的系统响应是否一致，幅频特性是系统响应的主要体现。

本小节在相同的电路参数与闭环控制器的配置条件下，对陀螺系统的等效传递函数、Simulink闭环模型以及实际陀螺的幅频特性进行仿真或测试，得到对应的幅频特性曲线。通过对比理论模型与实际陀螺测试数据的幅频特性曲线，验证系统建模的准确性。

对式（12）的闭环传递函数进行 Matlab仿真，得到系统Bode图，即幅频特性曲线，如图11所示。根据其 Bode图可知，标度因子约为4.51，3dB带宽117Hz。

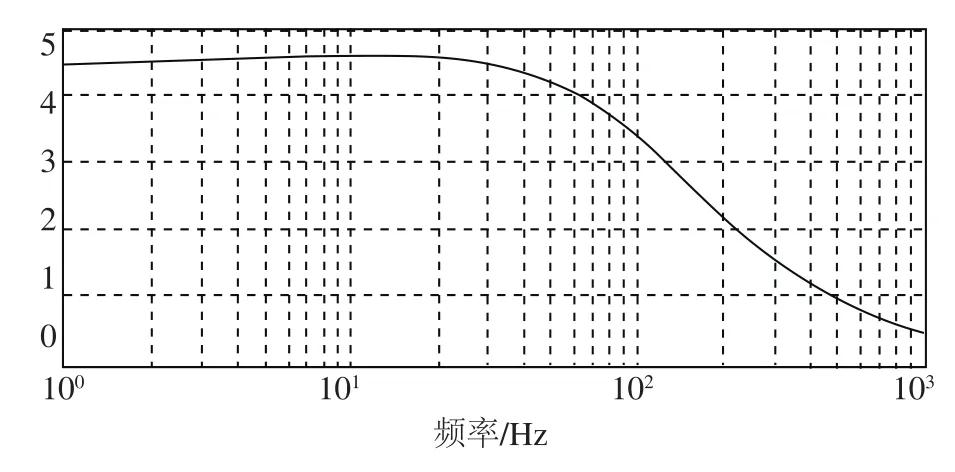
图11 陀螺闭环检测系统Bode图Fig.11 Bode diagram of gyro closed system

另外，针对如图5所示的陀螺闭环Simulink模型，分别对多个频率点的输入—输出频率响应进行仿真。并和随机抽取的一只MEMS陀螺进行相同频率点的频响特性进行测试，将两种曲线进行对比，得到如图12所示的幅频特性响应曲线。

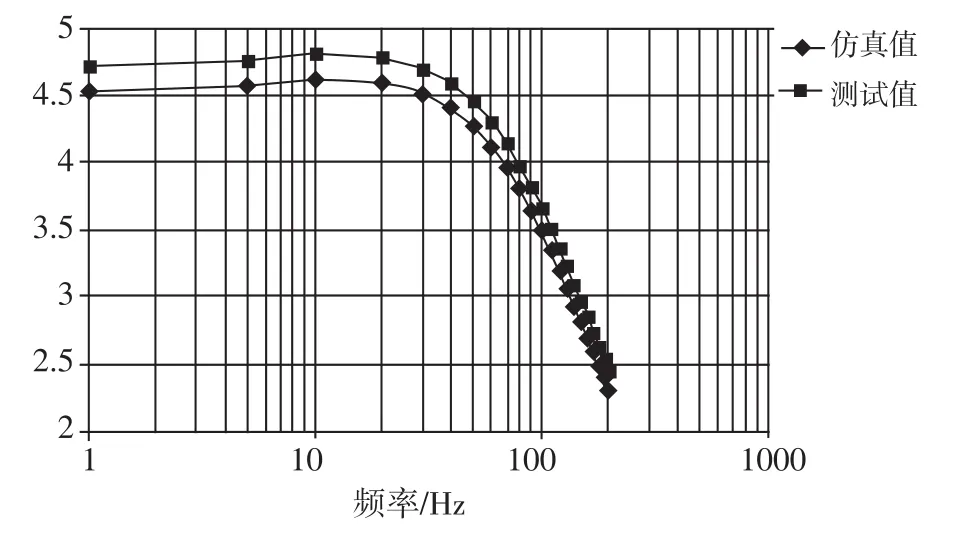
图12 Simulink闭环仿真与陀螺实测幅频对比曲线Fig.12 Comparison between Simulink simulation result and the real gyroscope test result

如图12所示，陀螺Simulink模型的标度因子为4.53，实测陀螺的标度因子为4.72；Simulink模型3dB带宽为116Hz，实测陀螺3dB带宽为120Hz。

将陀螺实测数据与传递函数、Simulink模型进行对比，结果如表1所示。

通过对比测试可知：包括等效传递函数与Simulink模型在内的理论建模，其幅频特性曲线趋势一致，带宽和标度因子的误差均小于5%。因此，本文建立的陀螺理论模型可以反映真实的陀螺检测系统。

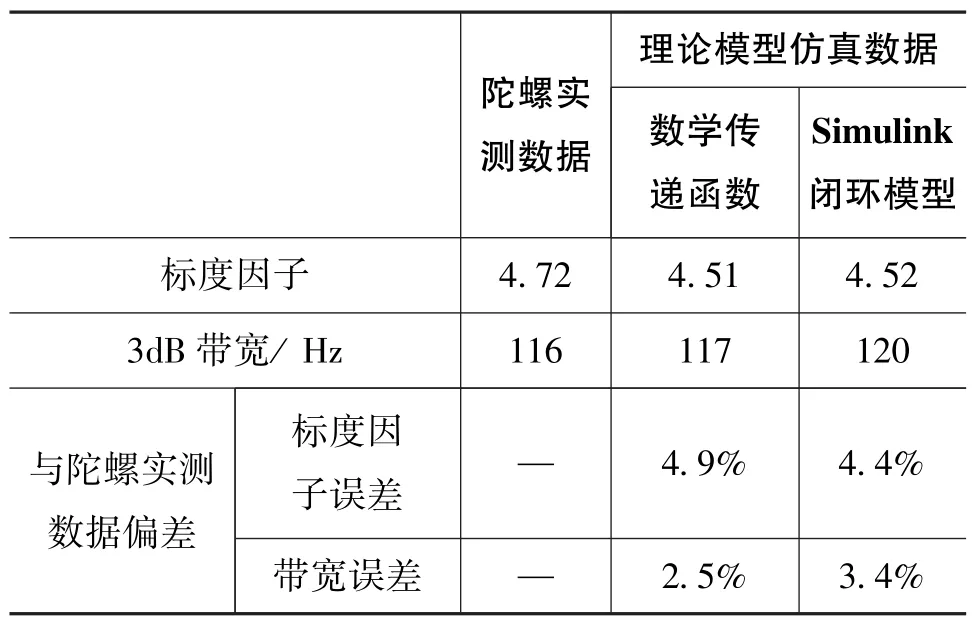
表1 理论模型与实测数据的对比Table 1 Comparison between theoretical model and real gyroscope test result

3.2 零偏稳定性

陀螺零偏稳定性是重要的精度指标，通过对陀螺闭环检测的信号通路中陀螺表头机械噪声、与C－V电路噪声进行建模，并进行闭环仿真，得到理论模型下陀螺的零偏稳定性。同时，对陀螺随机抽取5个样品进行测试，得到相应的零偏稳定性值并进行对比，结果如表2所示。

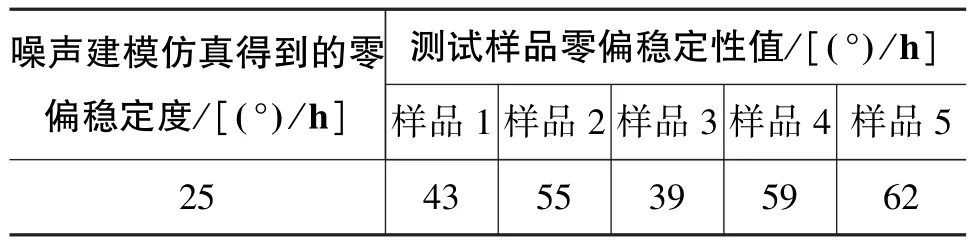
表2 Simulink模型与陀螺样品的零偏稳定性对比Table 2 Comparison of zero bias stability between Simulink model and gyroscope DUT

通过仿真与实际测试对比，陀螺零偏实际测试值分布较分散，且均比仿真值大，约为仿真值的1.5～2.5倍。经分析，出现这种情况的原因大概有：1）影响陀螺零偏稳定性的噪声源很多，仿真所用的噪声源没有包括所有的噪声源；2）其他因素（如温度漂移）引起的长期漂移也会对零偏稳定性产生影响。

4 结论

本文针对一款MEMS可配置的数字化陀螺，基于Simulink建立机电一体化陀螺系统模型，并对模型等效简化，推导了陀螺检测系统的闭环传递函数。通过分析对比理论模型与陀螺实测的系统响应特性与参数，验证了模型的有效性。借助该模型，可对陀螺检测环路进行系统优化、噪声模拟、指标分析，并根据陀螺系统指标约束，进行电路参数的配置。

[1]Bryan G H.On the beats in the vibrations of a revolving cylinder or bell[C].Proceedings of the Cambridge Philosophical Society，1980，7（3）： 101-111.

[2]Putty M W.A micromachined vibrating ring gyroscope[D].University of Michigan，1995.

[3]Cho J Y.High-performance micromachined vibratory rate and rate-integrating gyroscopes[D].University of Michigan，2012.

[4]Acar C，Shkel A.MEMS vibratory gyroscopes： structural approaches to improve robustness[M].Springer Science＆ Business Media，2009.

System Modeling，Simulation and Parameter Analysis of MEMS Vibrating Ring Gyroscope

WANG Hao，YE Ze-gang，ZHANG Qi-rong，QUAN Hai-yang
（Beijing Microelectronics Technology Institute，Beijing 100076）

There is an MEMS vibrating ring gyroscope based on a digital configuration，its mathematical modeling of gyro head and signal processing circuit is implemented，parameters’ mathematical relationship between gyro detection system and electromechanical characteristic is deducted，it can provide theoretical support for the configurable ASIC circuit.The validity and accuracy of the model are verified by comparing and analyzing the measured head data and theoretical model data.

MEMS； vibrating ring gyroscope；system modeling；digital configuration

V241.5

A

1674-5558（2017）02-01460

10.3969/j.issn.1674-5558.2017.06.006

2017-08-22

王浩，男，博士，微纳米系统设计技术专业，研究方向为MEMS惯性传感器设计。