干涉式光纤陀螺光纤环互易性温变漂移补偿方法
杨智杰,陈国光,朱宜家,范 旭,白敦卓
(1.中北大学机电工程学院,太原030051;2.豫西工业集团有限公司,南阳473000)
干涉式光纤陀螺光纤环互易性温变漂移补偿方法
杨智杰1,陈国光1,朱宜家1,范 旭1,白敦卓2
(1.中北大学机电工程学院,太原030051;2.豫西工业集团有限公司,南阳473000)
分析了干涉式光纤陀螺光纤环受温度影响产生零漂误差的机理,对于温变环境下的光纤陀螺输出,在传统线性分析手段的基础上,以互易性为主,把光纤环径向内外温度差以及温度变化率的差作为研究对象,建立了新的多项式零漂评估方法。通过对模型不同幂级次的探寻,寻找到变温情况下的最佳拟合系数并进行仿真补偿,实现了陀螺精度的大幅提高,使得最佳零漂降低为原始输出的20.6%。最后,对拟合系数进行陀螺变温实验验证,证实了该新型温度补偿方法的合理性。
光纤陀螺;互易性;零漂;线性多项式;温度补偿
0 引言
光纤环作为光纤陀螺的主要元器件之一,温度对其造成的非互易性误差是导致光纤陀螺在温变环境下测量精度大幅降低的主要因素[1]。Shupe效应的提出使得定量分析温度对光纤环性能的影响成为了可能,为光纤陀螺温变环境下精度提高的实现提供理论依据。为了克服Shupe效应的影响,多种光纤陀螺光纤环温度补偿方法被提出,整体分为光纤环结构改善和温度非互易性零漂算法补偿[2]。
对于光纤环结构的改善,1983年,Frigo提出了四极绕环方法,光纤环结构更加对称,在其受温度影响时光纤环产生互易性的温度扰动,从而降低Shupe效应的干扰[3]。在此基础上,双桶式、八极绕环等方法被相继提出。除了改变光纤环结构,1986年,Bednarz采取特殊的光纤环封装技术来降低温度对陀螺的影响[4]。伴随着光纤环结构改善的科技研究趋于饱和[5-7],软件补偿即通过仿真模拟,实现变温环境下光纤环零漂误差预估成为陀螺精度提高的另一主要手段。光纤陀螺光纤环温度补偿算法目前分为两大类:非线性建模与线性建模。其中,非线性建模国内已有人通过神经网络达到了较好的仿真效果[8-10],但由于其复杂的算法,不便于实时仿真陀螺输出[11]。线性建模则是国内研究最多的建模方式,主要基于最小二乘法,拟合线性多项式系数,为了实现工程化,其中的变量多采用时变的温度参数作为自变量[12-13]。
本文从光纤环的自身结构出发,以互易性思想为主,以四极对称式绕制的光纤环垂直高度中点出发,新颖地在径向方向,把温度梯度、温度变化率的差以及两者的交叉项作为研究对象,通过探寻合适的幂级次系数,实现光纤环温度补偿。
1 光纤环零漂误差产生机理
Shupe效应原理如图1所示,光纤陀螺中传播的光(C处)经过Y波导分束后,将会产生分别由顺逆时针方向通过光纤环的分束光,A处为顺时针方向传播光,B处为逆时针方向传播光。光纤环总长度为L,在t时刻顺时针传播的光与光纤环中点距离为,记该点为dz。当这一点受到温度扰动时,顺时针传播的光偏振态会发生变化。若此后光纤环再无温度扰动,那么逆时针传播的光在经过dz点时,将不会发生偏振态变化。如此两分束光在光纤陀螺系统探测器产生的干涉信号较无温度扰动的情况就会发生改变,从而产生陀螺误差[14]为:


图1 Shupe效应原理Fig.1 Principle of Shupe effect
当光纤环周围的温度随时间而变化时,由此产生的非互易性零漂误差便是以上对应的Shupe效应。为了解决该效应引起的零漂,四极对称式光纤环绕环技术应运而生。但是由于其结构原因,光纤环具有一定的绕环厚度,同一直径方向上的光纤因热导率而温度不同,导致热膨胀不一致,可能在某处产生严重的双折射应变。其次,由于光纤环同一直径方向上的光纤温度变化率不同,也会导致光偏振态变化。因此,为了简化模型,我们认为当光纤环周围环境温度变化时,其轴向温度变化相同,零漂特性主要受和时间相关的两个径向温度变量影响:温度变化率和温度梯度。温度变化率影响是指当温箱以不同的速率使得箱内温度由某一值变化至另一值时,光偏振态变化导致光纤环产生的零漂误差。温度梯度影响是指光纤环在同一直径方向的不同点处,温度随周围环境温度变化不同,即热传导不同,使得产生热应力,导致零漂。本文的模型基础是以线性拟合为方针,研究温度梯度、温度变化率的差以及两者的交叉项在不同幂级数模型的仿真效果。
2 光纤陀螺温度漂移补偿建模
光纤环内外侧中点温度测试如图2所示,黑色贴片为温度传感器。默认同一圆周上各点温度以及变化相同,以光纤环垂直高度中点内外侧温度数据为依托,根据陀螺系统互易性原理,建立模型。把光纤陀螺输出记为因变量F(K),把影响输出的两个温度变量:光纤环内外侧温度变化率的差和温度梯度分别记为自变量和2T(K)。

图2 光纤环内外侧中点温度测试Fig.2 Temperature test of optical fiber inner and outer midpoint
以上这两个因素主要影响陀螺输出的仿真公式可以用一次线性多项式表示:

其中,T(K)为温度与时间的函数,K为采样点序数。
式(2)为一次线性拟合表达式,也是最常用的温度补偿模型。在此基础上可以发展出二次、三次甚至多次线性拟合模型,但是这个模型忽略了多次交叉项可能引起的误差。考虑到两个变量的多次交叉项可能带来的影响,本文提出了新的模型,如式(3)所示:

当n等于2时,有:

当n等于3时,有:

依次类推,通过Matlab软件拟合出不同n值对应的Cj系数,探求n的最佳值,从而求解补偿后的陀螺输出零漂。
3 仿真与实验验证
为模拟光纤环所处的变温环境,并控制变量,仅将搭建好的光纤陀螺系统光纤环(长300m)放置于温箱中,通过对温箱进行程序设定,使温箱内的温度在-40℃~+70℃范围内变化,同时记录陀螺系统的零偏,从而得到陀螺系统的零偏与温度及温度变化速率的关系。程序在20℃、-40℃和70℃这3个温度点均保温2h,实验过程如下:
1)在20℃室温环境下保温2h;
2)以温箱最快速度从20℃降温到-40℃;
3)在温度为-40℃下保温2h;
4)以 1℃/min 的升温速率从 -40℃ 升温到70℃;
5)在温度为70℃下保温2h。
图3为陀螺零偏与温度变化曲线。其中,虚线为温度变化曲线;实线为陀螺输出曲线,该输出没有去除地球自转影响。
本文以100s的数据为基础进行拟合,拟合了两部分,分别是图3中的降温部分和升温部分。升温部分即截取图3中横坐标230~380之间的数据。通过式(3)进行拟合,当n分别为 1,2,3,…,21时,补偿后的零漂值结果有明显的递变规律:先减小再增大,当1≤n≤10时,补偿后零漂都是降低,因此截取11≤n≤21的数据,如表1所示。由表1中数据可得规律:当n=18时,达到的补偿效果最好,升温段原始输出的零漂为0.1751,补偿后的零漂为原始输出零漂值的5.3%。图4为升温段陀螺输出拟合曲线,在温度变化时,拟合曲线与原输出曲线基本吻合。

图3 陀螺零偏与温度变化曲线Fig.3 Variation curve of gyro bias and temperature

图4 升温段陀螺输出拟合曲线Fig.4 Fitting curve of gyro output in warming up section
在降温部分,截取图3中横坐标50~150之间的数据,通过式(3)进行拟合,当n分别为1,2,3,…,11时,补偿后的零漂值结果如表2所示。根据表2数据可知,当n=8时,达到的补偿效果最好,降温段原始输出的零漂为0.1411,提升了94.7%。图5为降温段陀螺输出拟合曲线,在温度变化时,拟合曲线与原输出曲线基本吻合,升温段的拟合较之降温段较差。在升温过程中,实验现场温箱机箱的振动较降温过程中剧烈许多,由此引入的振动是导致非互易性的主要因素。

表1 升温段拟合次数n与补偿后零漂值Table 1 Fitting time n and value of zero drift after heating

表2 降温段拟合次数n与补偿后零漂值Table 2 Fitting time n of cooling section and value of zero drift after compensation

图5 降温段陀螺输出拟合曲线Fig.5 Fitting curve of gyro output at cooling stage
为了验证模拟系数的正确性,对陀螺进行了重复实验,所测结果如图6所示。

图6 陀螺变温重复测试Fig.6 Repetition test of gyro variable temperature
以拟合的升温段系数以及降温段系数直接对图6中的升温部分以及降温部分进行拟合,所得结果如图7所示。
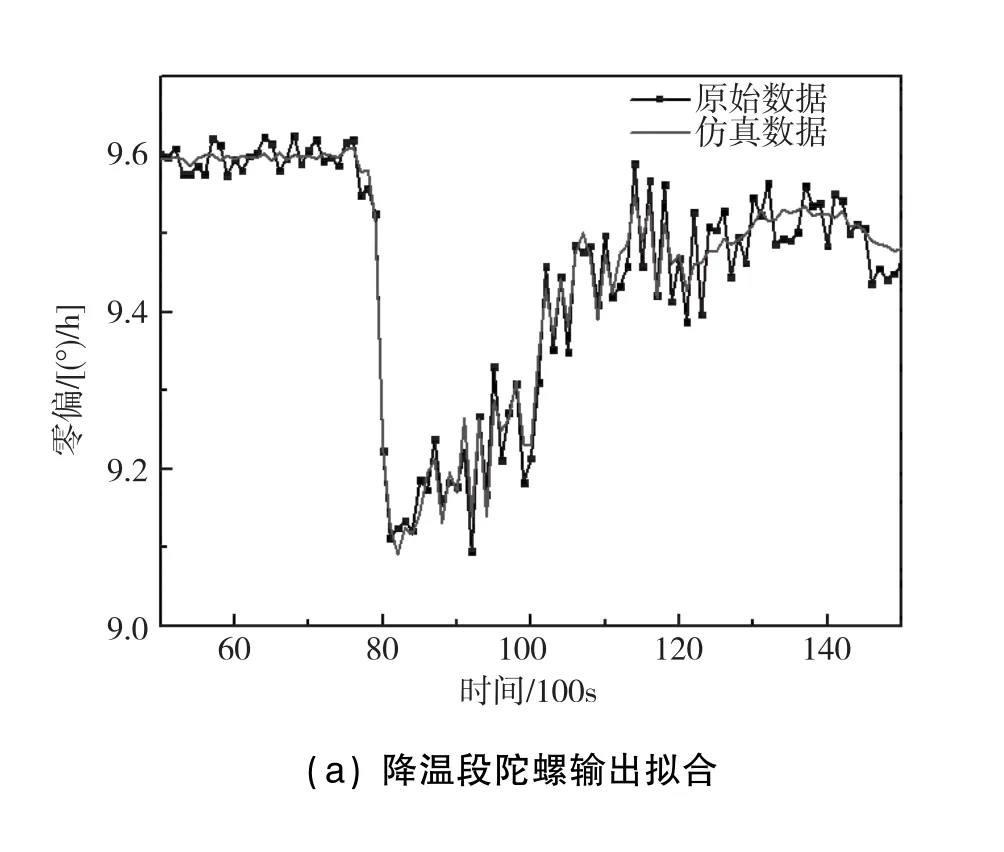

图7 仿真验证Fig.7 Simulation verification
通过重复实验的验证,降温段原始零漂为0.1514,拟合补偿后零漂为0.0313。升温段原始零漂为0.1720,拟合补偿后零漂为0.0629。重复实验后的拟合效果有所下降,原因可能是温箱的重复性较差。但是可以证明,以互易性为基础,把径向温度梯度和温度变化率的差作为自变量的陀螺温度补偿模型具有合理性。
4 结论
通过分析温度对光纤环结构互易性影响,以径向温度梯度、温度变化率的差以及两自变量的交叉项作为研究对象,简化并建立了新的线性多项式拟合模型,对两种不同温变情况下的数据进行仿真,实现了大幅度降低陀螺零漂的目的。实验结果表明,使得最佳零漂降低为原始输出的20.6%,证明了理论的合理性。
从补偿的结果来看,不同温变环境下的温度补偿拟合系数不同,补偿后依然存有温度误差,且测试环境中的振动以及光纤陀螺其他元器件都会导致实际测试的温度误差高于拟合。陀螺实际应用中的温变环境更加复杂,更多温变状态下的陀螺输出的分段拟合及标定值得进一步研究。
[1]Lofts C M,Ruffin P B,Parker M D,et al.Investigation of the effects of temporal thermal gradients in fiber optic gyroscope sensing coils[J].Optical Engineering,1995,34(10): 2856-2863.
[2]韩冰,林玉荣,邓正隆.光纤陀螺温度漂移误差的建模与补偿综述[J].中国惯性技术学报,2009,17(2):218-224.HAN Bing,LIN Yu-rong,DENG Zheng-long.Overview on modeling and compensation of FOG temperature drift[J].Journal of Chinese Inertial Technology,2009,17(2): 218-224.
[3]Frigo N J.Compensation of linear sources of non-reciprocity in Sagnac interferometers[C].Proceedings of the SPIE,1983,412(6): 268-271.
[4]Bednarz B,Dankowych J A,Joslin G,et al.Optomechanical systems for a closed loop fiber optic gyroscope[C].Proceedings of the 10thAnniversary Conference,Cambridge,1986: 24-26.
[5]Liu R Y,El-wailly T F,Dankwort R C.Test results of Honeywell's first-generation high-performance interferometric fiber optic gyroscope[C].Proceedings of SPIE,The International Society for Optical Engineering,1992: 1585.
[6]Ruffin P B.Reduction of nonreciprocity noise in wound fiber optic interferometers[J].Optical Engineering,1994,33(8): 2675-2679.
[7]Ruffin P B,Smith R H.Fiber winding approaches for environmentally robust IFOG sensor coils[C].Proceedings of SPIE 1792,Components for Fiber Optic Applications VII,1993: 179-189.
[8]王志勇.光纤陀螺温度漂移的小波神经网络[J].激光杂志,2016,37(5): 85-88.WANG Zhi-yong.Wavelet neural network for static temperature drift of fiber optic gyro[J].Laser Journal,2016,37(5): 85-88.
[9]周琪,秦永元,赵长山.光纤陀螺温度漂移误差的模糊补偿方案研究[J].传感技术学报,2010,23(7):926-930.ZHOU Qi,QIN Yong-yuan,ZHAO Chang-shan.Research on fuzzy compensation method of temperature drift for fiber optical gyro[J].Chinese Journal of Sensors and Actuators,2010,23(7): 926-930.
[10]赵曦晶,汪立新,何志昆,等.光纤陀螺温度漂移建模补偿[J]. 压电与声光,2013,35(4): 528-532.ZHAO Xi-jing,WANG Li-xin,HE Zhi-kun,et al.Modeling and compensation of FOG temperature drift[J].Piezoelectrics & Acoustooptics,2013,35(4): 528-532.
[11]金靖,宋凝芳,李立京.干涉型光纤陀螺温度漂移建模与实时补偿[J]. 航空学报,2007,28(6): 1449-1454.JIN Jing,SONG Ning-fang,LI Li-jing.Temperature drift modeling and real-time compensation of interferometric fiber optic gyroscope[J].Acta Aeronautica Et Astronautica Sinica,2007,28(6): 1449-1454.
[12]冯卡力,李安,覃方君.基于多模型分段拟合的光纤陀螺温度误差补偿方法[J].中国惯性技术学报,2014,22(6): 825-828.FENG Ka-li,LI An,QIN Fang-jun.Temperature error compensation method for FOG based on multi-model piecewise fitting[J].Journal of Chinese Inertial Technology,2014,22(6): 825-828.
[13]王俊璞,金志华,田蔚风.光纤陀螺温度漂移的多变量模型[J]. 光电工程,2008,35(5): 66-69.WANG Jun-pu,JIN Zhi-hua,TIAN Wei-feng.Multivariable modeling strategy for the fiber optic gyro temperature-dependent drift[J].Opto-electronic Engineering,2008,35(5): 66-69.
[14]张桂才.光纤陀螺原理与技术[M].北京:国防工业出版社,2008.ZHANG Gui-cai.Principle and technology of fiber optic gyroscope[M].Beijing: NationalDefense Industry Press,2008.
Reciprocal Temperature Bias Drift Compensation Method for Fiber Coil of Interferometry Fiber Optical Gyroscope
YANG Zhi-jie1,CHEN Guo-guang1,ZHU Yi-jia1,FAN Xu1,BAI Dun-zhuo2
(1.School of Mechanical and Electrical Engineering,North University of China,Taiyuan 030051;2.Yuxi Industries Group Co.,Ltd,Nanyang 473000)
The mechanism of drift caused by temperature of interferometry fiber optical gyroscope (IFOG)is analyzed.The new polynomial model based on the traditional method is connected with temperature difference and variety rate in radial direction of fiber coil and used to emulate the outputs of IFOG for two different temperature environments.Through the research on the mathematical laws of model series of power function,the ideal series of the new model for the two different environments are found.The new polynomial model improves the accuracy of IFOG substantially.It could make the bias drift of new polynomial reduce to 20.6%.At the end,the new polynomial model is verified by testing the bias drift of IFOG in varying temperature environment and the model is reasonable.
fiber coil;reciprocity;zero drift;linear polynomial;temperature compensation
V241.5
A
1674-5558(2017)02-01415
10.3969/j.issn.1674-5558.2017.06.008
2017-05-24
杨智杰,男,硕士,兵器科学与技术专业,研究方向为弹体姿态测量和陀螺仪精度分析。

