1 000 MW直流炉机组非线性动态模型及闭环验证

范 赫, 张雨飞, 苏志刚, 王培红

(东南大学 能源与环境学院，能源信息与自动化系，南京 210096)

1 000 MW直流炉机组非线性动态模型及闭环验证

范 赫, 张雨飞, 苏志刚, 王培红

(东南大学 能源与环境学院，能源信息与自动化系，南京 210096)

为获得适用于大范围变工况的超超临界机组机理模型，采用机理分析法建立了协调控制系统(包括制粉系统、锅炉系统和汽轮机系统)模型，输入量为燃料量指令、总给水量和汽轮机调门开度，输出量为汽水分离器蒸汽焓值、主蒸汽压力和机组功率.在参数辨识方面，静态参数采用机组稳态运行数据结合非线性回归分析获得；动态参数采用免疫遗传算法,结合大范围变工况运行数据求取，最后对所建立的机理模型进行静、动态模型验证.结果表明：此协调控制系统模型具有正确、简单的机理模型结构和较高的精度，可用于控制算法测试和协调控制系统设计.

超超临界机组； 机理模型； 参数辨识； 免疫遗传算法； 模型验证

随着全球温室效应加剧，为了减少CO2排放，中国能源行业急需由高能耗、低效率走向低能耗、高效率道路.超超临界锅炉具有大容量、高温高压的特点(主汽温度最高可达610 ℃，主汽压力最高可达31 MPa),能够显著提高机组循环热效率，减少污染物排放，其循环热效率为43%～49%，供电煤耗为260～290 g/(kW·h)，比亚临界机组循环热效率提高了10%，供电煤耗减少70～90 g/(kW·h)，总污染物排放量减少25%～30%[1]，超超临界机组有取代亚临界机组的趋势.近几年，可再生能源(即水电、风电和核能等)发展迅速[2]，但其供电不稳定性会导致电网频率不稳定.对于在役超超临界机组，必须具有较好的负荷调节能力，来保证电网安全稳定运行.

在电厂众多控制系统中，协调控制系统(CCS)既可以快速调整机组负荷，满足电网对负荷和频率的要求，还能维持锅炉与汽轮机的安全高效运行，在火电机组与电网之间扮演着重要角色.典型CCS中，控制量为燃料量指令、总给水量和汽轮机调门开度，被控量为分离器蒸汽焓值、主蒸汽压力和机组功率.当负荷指令上升时，汽轮机调门开度增大，释放汽水和金属中的潜热，增加进入汽轮机的能量来满足外界负荷需求.同时，通过增加燃料量、给水量和相关风量来恢复机组储能，协调锅炉与汽轮机的动态特性差异，维持机组与外界的能量平衡，即为机组协调控制的基本原则.因此，能准确反映机组运行特性的模型对于协调控制系统的设计十分重要.

Liu等[3]采用模糊神经网络建立超超临界机组模型，并与最小二乘和径向基函数(RBF)神经网络建模法进行比较，结果表明模糊神经网络建模法具有很高的精确度；马良玉等[4]采用神经网络建立某600 MW超临界机组负荷和主汽压力的数学模型，结果表明此模型可以很好地拟合机组负荷、主蒸汽压力与燃料量以及给水量和汽轮机调门开度间复杂的非线性动态特性.在机理建模方面，秦志明等[5]通过分析制粉过程、锅炉受热、过热器和汽轮机系统的动态特性，建立直流炉机组非线性动态模型；徐蕙等[6]采用变相变点方法建立超超临界直流炉水冷壁热水段、蒸发段和过热段长度随锅炉负荷变化的动态仿真模型；Liu等[7]建立了1 000 MW直流炉简化机理模型，此模型忽略相变点变化，结构简单，能够反映复杂的直流炉机组运行特性.

在参数辨识方面，遗传算法不需要完整的系统模型且具有显著的搜索能力，已被广泛应用于模型参数优化.闫姝[1]采用遗传算法优化动态模型参数,经过大范围运行数据验证表明，此模型具有一定精度.Sindareh-Esfahani等[8]采用遗传算法优化模型参数，使模型输出与实际数据一致.但由于此算法易陷入局部最优点且无最优个体保存机制，导致搜索后期类似随机搜索，使得所求解的精确度较低.免疫遗传算法(IGA)是将人体免疫与遗传算法相结合，通过基于抗体浓度的选择机制，丰富种群复杂度；并通过记忆细胞接种来保存种群最优抗体，提高收敛速度.与遗传算法相比，通过IGA优化的解精确度更高.Chen等[9]采用IGA确定支持向量机的最优参数,验证结果表明此模型具有较强的泛化能力.

笔者采用机理与数据分析法，建立了某1 000 MW超超临界机组的非线性动态机理模型.在干态运行条件下，将机组受热面看成一根等容受热管，通过简化和假设得到机组协调控制系统机理模型结构.在参数辨识方面，通过稳态数据和非线性回归分析获得静态参数；将IGA与大范围变工况数据结合优化出动态参数.最后对所建模型进行闭环验证.

1 模型建立

1.1 研究对象

以安徽省皖能股份有限公司某1 000 MW超超临界机组为建模对象.锅炉型号为SG-3012/27.9-M540，为超超临界参数变压运行螺旋管圈直流炉，采用一次中间再热.汽轮机型号为N1055-27/600/600(TC4F)，为超超临界、一次中间再热、单轴、四缸四排汽、双背压、八级回热抽汽、反动凝汽式汽轮机.表1给出了机组在额定工况(THA)下的运行参数.

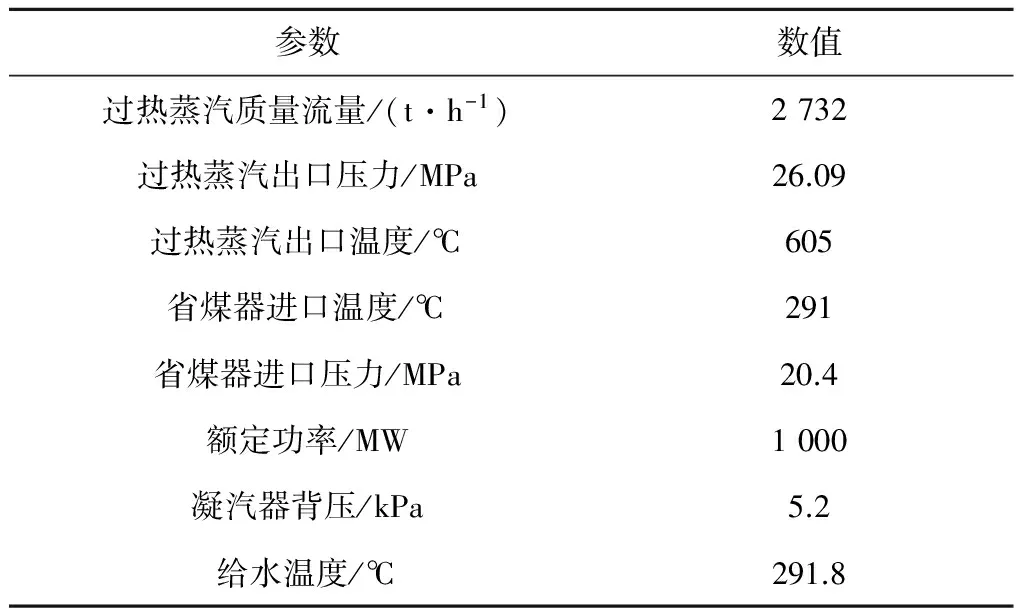
表1 额定工况下的运行参数

1.2 制粉系统建模

在大容量燃煤机组中，常采用直吹式制粉系统.储存在储煤仓的煤由给煤机的传送皮带传送到磨煤机，经过破碎和研磨，合格的煤粉被一次风送入燃烧器，在炉膛内燃烧.整个过程可用延迟和惯性环节来描述.

给煤机和一次风管道的主要动态特性是延迟，其纯延迟环节为：

(1)

制粉系统的惯性特性表现在磨煤机中，其质量平衡方程为：

(2)

式中：rB为实际入炉煤量,kg/s;M为磨煤机内存煤量，kg.

根据磨煤机特性，实际入炉煤量可表示为：

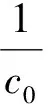
(3)

式中：cB为磨煤机基本出力系数；fH为煤的可磨性修正指数；fW为煤水分修正系数；fR为煤粉细度修正系数；以上系数的乘积，可用c0的倒数来替代，c0为制粉惯性时间,s.

综上所述，可得制粉系统传递函数为：

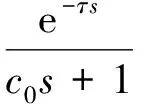
(4)

1.3 锅炉建模

在保证模型准确的基础上，降低结构复杂度，结合超超临界锅炉特点，在机组干态运行条件下，将省煤器、水冷壁、汽水分离器和过热器等受热面看成一根等容受热管，建模时只考虑进、出口参数和集总参数的变化.

不同负荷下，保持主汽温稳定的根本措施是保持一定的燃水比，减温喷水作为辅助手段，来降低因燃料量和给水量的动态差异而产生的主汽温波动.在机组安全稳定运行时，可取消减温水来简化模型结构，即

qm,sm=qm,fw

(5)

式中：qm,sm为进入省煤器的给水量，kg/s;qm,fw为总给水量, kg/s.

在锅炉建模时可进行如下简化和假设：

烟气侧，(1)忽略工质，烟气和管壁之间的轴向传热；(2)忽略烟气侧工况的动态变化过程；(3)锅炉吸收热量与实际燃料放热量成正比；(4)烟气放热量沿管长均匀分布.

锅炉侧，(1)受热管横截面上的流体特性均匀；(2)为了方便计算，将实际汽水分离器压力的测量值pm和汽水分离器蒸汽焓值hm近似为模型中pm和hm，且动态参数c1和c2具有一定的修正作用.

图1中，简化后的锅炉部分可分为省煤器、水冷壁、汽水分离器和过热器.来自回热系统的给水依次经过上述受热面吸收热量，最终转变为额定参数的过热蒸汽.

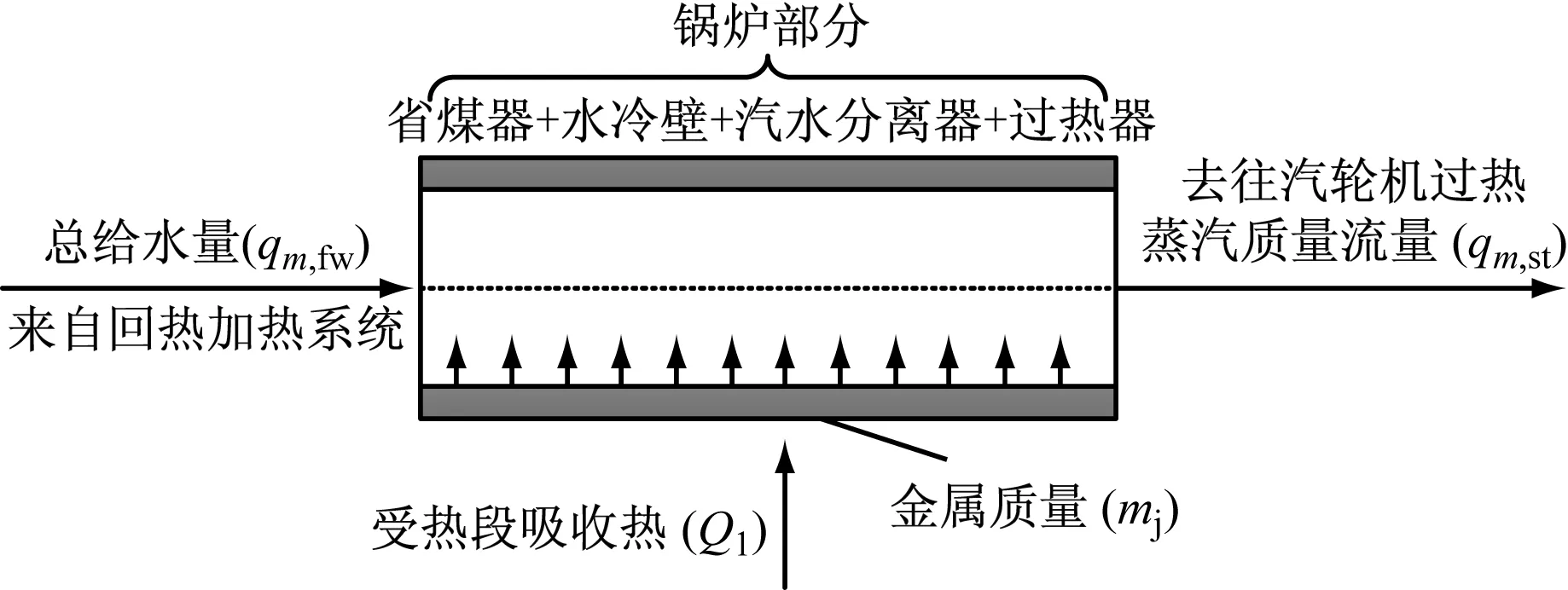
图1 直流炉简化图

由于汽水分离器焓值是最早体现汽水系统中煤水比失调的信号，且汽水分离器压力能很好地跟踪机组负荷变化[10]，因此选择汽水分离器中的工质参数作为集总参数.受热段的动态特性可用质量和能量平衡方程表示，可得：

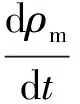
(6)

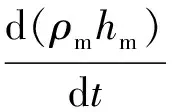
qm,sthst+Q1

(7)

Q1=k1rB

(8)

式中：s1、s2为动态参数；cj为受热段金属比热容，kJ/(kg·K)；mj为受热段金属质量, kg;Tj为金属壁温, ℃;ρm为汽水分离器出口蒸汽密度，kg/m3;hm为汽水分离器蒸汽焓值，kJ/kg;qm,st为主蒸汽质量流量，kg/s;hfw为给水焓值，kJ/kg;hst为主蒸汽焓值，kJ/kg;Q1为锅炉吸热量，kJ/s;k1为工质吸热量增益，kJ/kg；下标m、fw、st和j分别代表汽水分离器处的状态量、给水状态量、主蒸汽处状态量和锅炉金属状态量.

由烟气侧假设(4)可认为各处受热段金属壁温的变化速率是相等的，即dTj/dt=dTjm/dt，其中Tjm为汽水分离器处的金属壁温，℃,并认为，Tjm≈Tm,Tm为汽水分离器工质温度，℃.

在过热蒸汽温度控制系统中，通过改变燃水比可使汽水分离器焓值保持在一定范围内，喷水减温作为辅助手段，来保证过热汽温稳定；通过改变燃料量指令、总给水量和汽轮机调门开度，使单元机组输出的实际功率跟踪外部负荷指令，且主蒸汽压力能反映锅炉与汽轮机之间的能量供求平衡.因此将汽水分离器蒸汽焓值、压力和入炉煤量作为模型状态参数，汽水分离器蒸汽焓值、主蒸汽压力和机组功率作为模型输出，燃料量指令、总给水量和汽轮机调门开度作为模型输入.在式(6)和式(7)中分别对pm和hm计算偏微分：

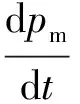
(9)

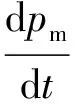
lqm,sthm+Q1

(10)

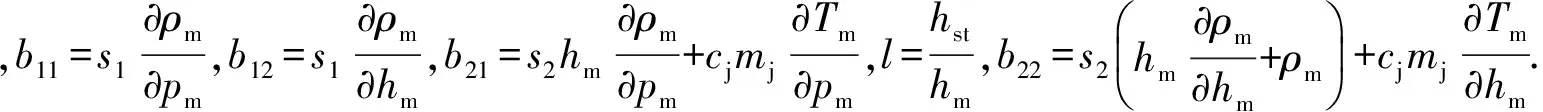
联立式(9)和式(10)可得：

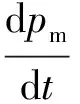
(d1-lhm)qm,st+Q1

(11)

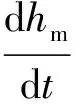
(d2-lhm)qm,st+Q1

(12)

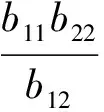
过热器中的压差与流量方程[10]为：

qV02+z2qV0Q0=z1Δp

(13)

式中：qV0为过热器管道内蒸汽的初始体积流量，m3/s;Q0为蒸汽经过过热器管道吸收的热量,kJ；Δp为蒸汽流经过热器管道产生的压差,Δp=pm-pst,pst为主蒸汽压力，MPa；z1、z2为与管道阻力、气体比热有关的系数.

由于qV0=qm0v0，其中v0为蒸汽初始比体积，m3/kg，qm0为过热器内蒸汽初始质量流量，kg/s，故式(13)可转换为式(14)：

(14)

qm0/Q0本质上即为煤水比的函数，hm可以准确快速地反映出煤水比变化.为了获得高精度且结构简单的模型，忽略hm的变化对压力-流量方程的影响，即认为hm为常数.

从能量平衡角度来看，Q0与机组负荷Ne成正比，而pm可以准确及时地反映Ne的变化[10]，v0=v(pm，hm)，因此：

Δp=g(pm)

(15)

式中：g(·)为一种函数关系.

1.4 汽轮机建模

进入汽轮机的主蒸汽流量方程[1]为：

(16)

式中：ρst为汽轮机进口蒸汽密度,kg/m3;ut为汽轮机调门开度；α为蒸汽状态参数.

由于ρst=ρ(hst,pst)，式(16)可写成：

qm,st=utf(pst,hst)

(17)

为获得高精度且结构简单的主蒸汽流量模型，根据数据分析,忽略hst对模型的影响(即认为hst为常数)，可得：

qm,st=utf(pst)

(18)

式中：f(·)为一种函数关系.

图2为广义汽轮机系统简化图.对汽轮机系统进行简化假设：(1)将回热系统纳入汽轮机系统，视为广义汽轮机系统；(2)在汽轮机系统中，忽略除氧器和凝汽器中的工质质量、能量损失；(3) 将高压缸、中压缸和低压缸汽轮机组看成一整台汽轮机；(4) 忽略汽轮机惯性和延迟；(5)将再热蒸汽吸热部分在汽轮机增益k2处进行修正；(6)机组正常运行时，汽轮机效率保持不变.

汽轮机功率表达式为：

Ne=k2(qm,sthst-qm,sthfw)

(19)

由于模型的简化和假设会引起建模误差，为提高模型精度，分别对hfw、l和k2进行建模.由数据分析可知，随着机组负荷的升高，工质的压力升高，给水焓值增加；本机组的过热器为对流式过热器，随着负荷的升高，l增大；再热蒸汽吸热量与过热蒸汽吸热量的比值随着负荷升高而增大[1]，k2也随着负荷的升高而增加，因此可得：

hfw=h(pm)

(20)

l=l(rB)

(21)

k2=k(rB)

(22)

式中：h(·)、l(·)和k(·)为一种函数关系.

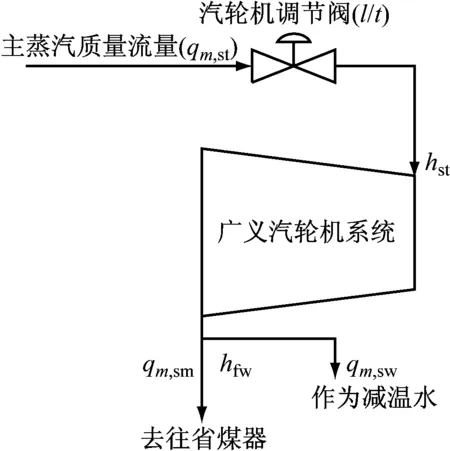
图2 广义汽轮机系统简化图

1.5 最简模型结构

综上所述，该直流炉机组非线性模型结构为：

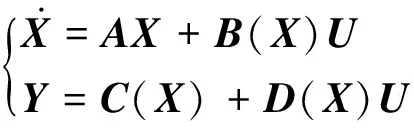
(23)

其中，

经整理，该机组非线性模型结构为：

(24)

2 参数辨识

上述机理模型共有4个静态参数k1、k2、l和hfw,6个动态参数τ、c0、c1、c2、d1和d2以及2个未知函数f(·)、g(·)需要辨识.

2.1 静态参数辨识

该系统的稳态方程为：

(25)

(26)

(27)

其中，*表示变量处于稳态.

结合式(19)，静态参数可通过稳态段数据和非线性回归分析得出：

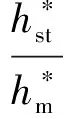
(28)

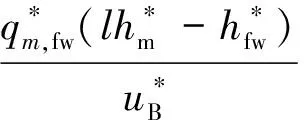
(29)

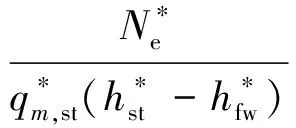
(30)

2.2 动态参数辨识

在满足闭环可辨识性[1]的基础上，选择大范围降负荷数据.工况1：时间段2016-03-18T06-00-00—2016-03-19T17-17-00，负荷段1 016.3～499.168 MW，采样周期T=1 s,共126 992个采样点，经过小波去噪、野值剔除等数据处理，并结合免疫遗传算法[11]，进行参数辨识.为加快寻优速度，采用一阶后向差分对上述连续系统进行离散化，设X={x1,x2,…,xn}为所有模型动态参数的集合，在获得静态参数及初始状态参数的基础上，将运行数据中的输入量导入模型进行迭代计算，并将所得状态参数作为下一时刻模型计算状态参数的初始值，则参数辨识问题为寻找一组动态参数(x*)，使得适应度函数E最小：

E(x*)=minE(xi),xi∈X

(31)

(32)

式中：Δpst、ΔNe和Δhm分别为模型计算所得主蒸汽压力、机组负荷和汽水分离器蒸汽焓值与实际值的偏差；pst0、Ne0和hm0分别为额定负荷下的主蒸汽压力、机组负荷和汽水分离器蒸汽焓值，本文中取pst0=26.09 MPa，Ne0=1 000 MW，hm0=2 984.32 kJ/kg.

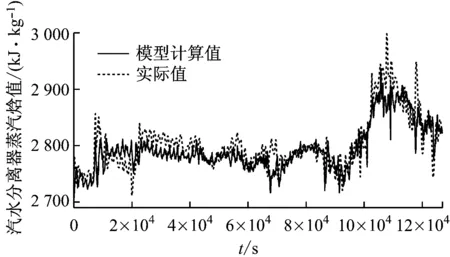
(b)

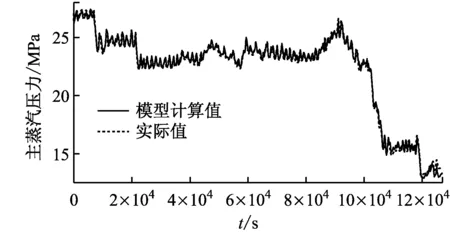
(c)

辨识所选数据与模型计算值的对比如图3所示.由图3可知，模型计算值与机组实际值吻合得很好,表明采用IGA寻优的动态参数使模型具有较高的精度.

经过完整辨识，得出：

静态参数

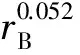
动态参数

τ=36,c0=279,c1=365 522,

c2=78 746,d1=582,d2=2 769

未知函数

f(pst)=43.52pst+10.57

输入量的范围为：

50 kg/s≤uB≤120 kg/s,400 kg/s≤

qm,fw≤800 kg/s,60%≤ut≤70%

将上述静态参数、动态参数和未知函数代入该机组非线性模型结构，可得1 000 MW直流炉机组在干态运行工况的非线性模型：

(33)

3 模型验证

3.1 稳态工作点验证

表2和表3给出了机组在不同稳定负荷下，机组实际值、模型计算值和各参数的相对误差.在该工况下，模型相对误差的绝对值不超过2.92%，最小值为0.002 3%，表明所建模型具有较高的稳态精度.

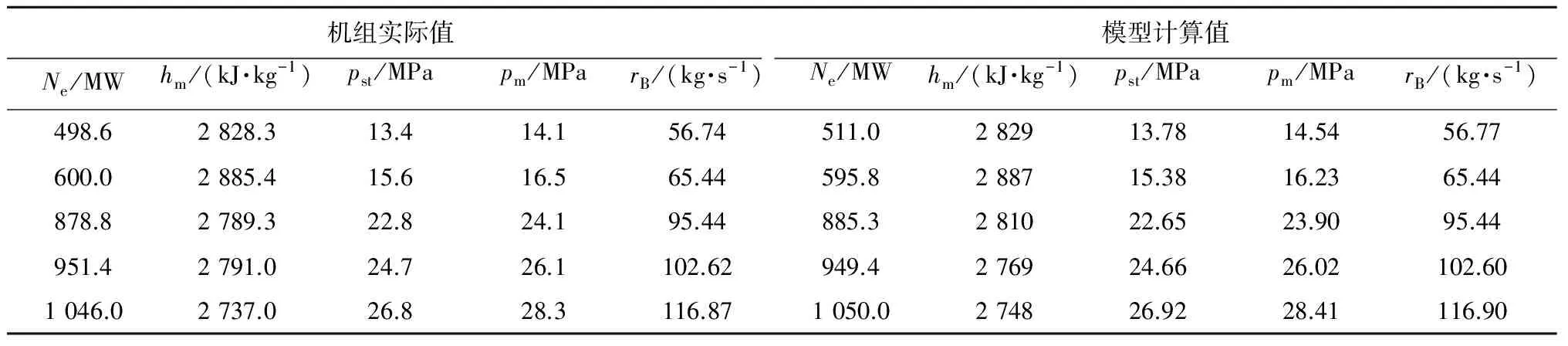
表2 不同稳定负荷下的机组实际值与模型计算值

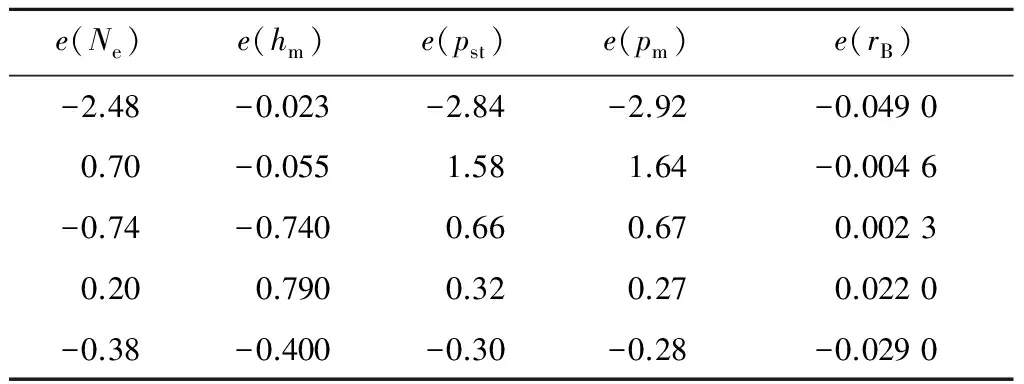
表3 不同稳定负荷下的模型相对误差e

3.2 动态模型验证

(a)

(b)

(a)

(b)

(c)

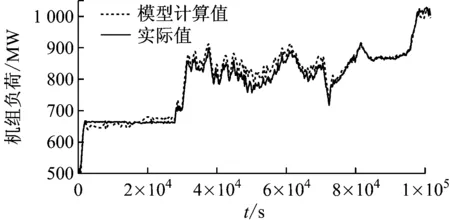
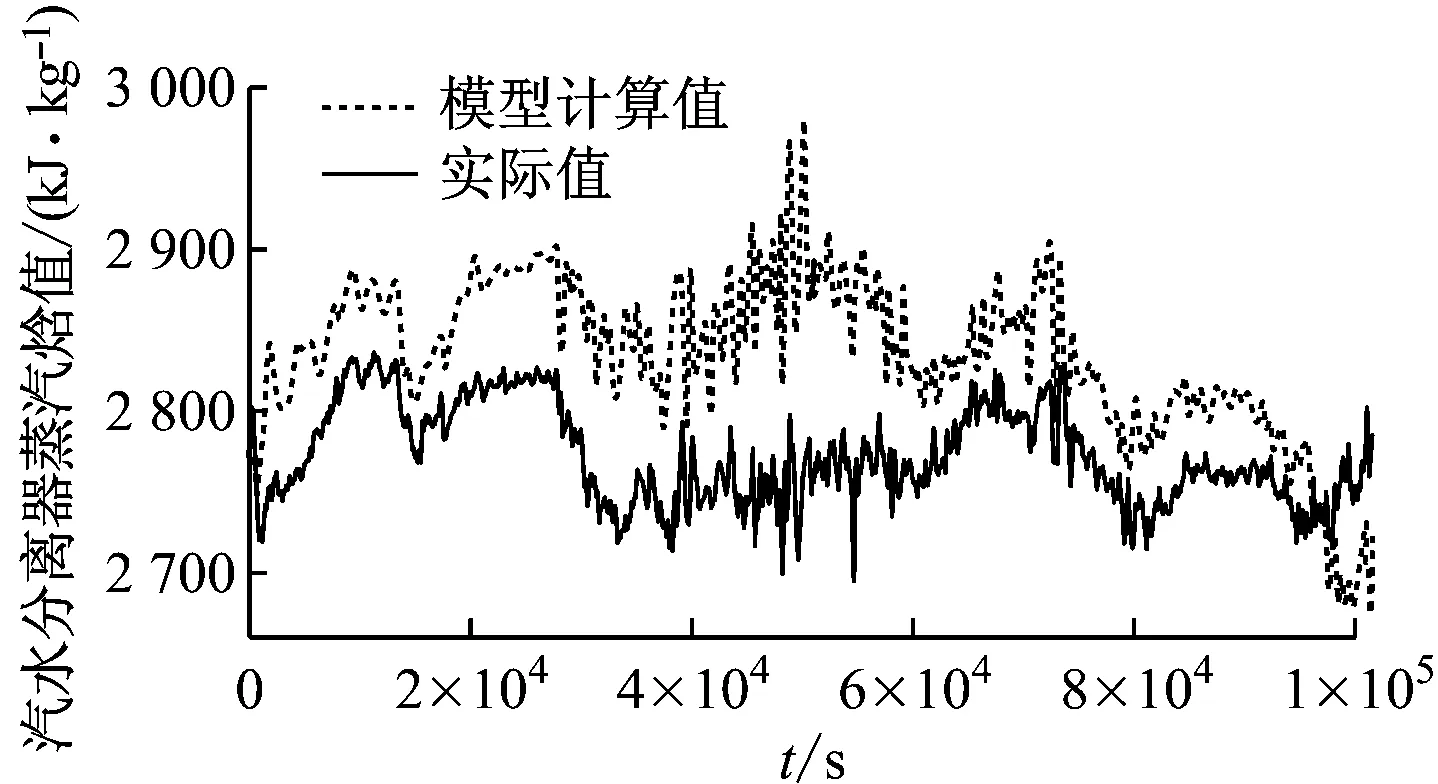
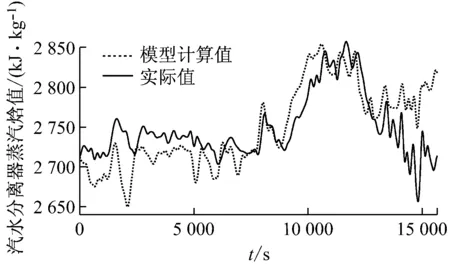
选择2段大范围变工况升降负荷数据，将模型计算值与实际值进行比较，验证变负荷情况下的模型准确性.2段运行数据均经过野值剔除、小波去噪，工况2：时间段2016-06-13T12-56-55—2016-06-14T17-10-59，升负荷段501.6～1 004.3 MW，采样周期T=1 s,共101 608个数据点；工况3：时间段2016-10-22T17-30-01—2016-10-22T21-51-25，降负荷段1 005.5～505.9 MW，采样周期T=1 s,共15 650个数据点.结果见图4和图5，其相对误差平均值见表4.

由图3～图5和表4可知，所建模型在机组大范围升降负荷变化中，可正确反映机组运行动态特性，相对误差平均值最大为2.45%, 最小为0.72%，表明此模型具有满意的动态精度.

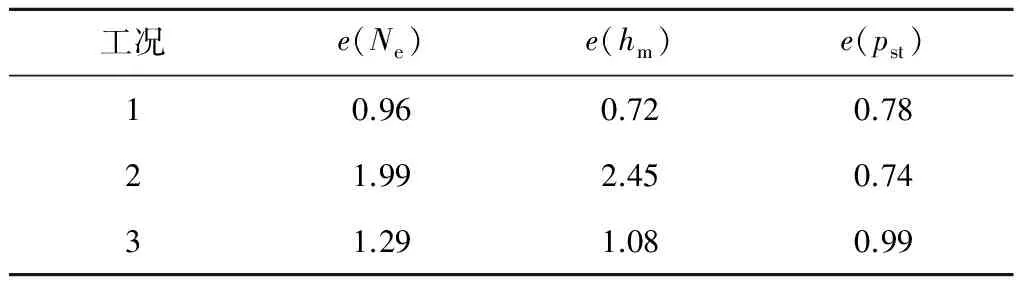
表4 模型相对误差平均值比较

4 结果与讨论

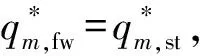
工况1中，模型的相对误差平均值是最满意的，说明：(1)IGA具有出色的参数寻优能力，可用于模型动态参数辨识；(2)对主蒸汽流量方程和压差-流量方程的简化是合理的，对模型的精确性影响较小；(3)从机理建模的角度来看，本模型可正确反映机组运行参数的变化，所建模型结构本质上是正确的.

另外，在大范围升、降负荷模型验证阶段，所建模型仍具有较高精度.但与工况1相比，偏差仍较大，原因如下：

(1) 时变参数.由于实际机组参数会随着运行工况发生变化.本文中将这些参数视为定值，本模型参数是由工况1求取的，因此对于工况2、工况3会产生一定误差.

(2) 煤质、机组效率和各子系统控制质量变化的影响.从能量平衡的角度分析，在机组效率不变的情况下，工质吸热量与机组负荷存在一一对应的关系，当函数关系确定后，煤质和锅炉效率变化会产生模型功率计算偏差；又由于汽轮机回热系统控制质量不高，实际给水焓值较低，从而导致给水焓值计算偏差，模型焓值输出值偏高，如图4(b)所示.

综上所述，在变负荷过程中，模型计算值与机组实际值变化趋势相同，吻合度较高，其中主蒸汽压力与实际值吻合最好，说明在机组实际运行中，由调节汽轮机调门开度来稳定主蒸汽压力，具有较小的延迟和惯性，机组功率由锅炉侧的燃料量和总给水量等控制，是典型的机炉协调运行方式，所以此模型适合协调控制系统设计.

5 结 论

(1) 根据质量守恒、能量守恒和热力学定律建立1 000 MW直流炉机组非线性机理模型，在干态运行工况下，将省煤器、水冷壁、汽水分离器和过热器看成一根等容受热管，并简化过热器中的压差与流量方程、主蒸汽流量方程，且忽略模型参数的时变性，从而获得简单的机理模型结构.

(2) 在获得静态参数和未知函数的基础上，采用免疫遗传算法结合大范围变工况数据，来获得更准确的动态参数，以提高模型精度.经过稳态、大范围升降负荷验证，表明此模型具有满意的动、静态精度，可在大范围运行工况下反映机组参数动态变化，适用于控制算法测试和协调控制系统设计.

致谢:在此衷心感谢王奔同学提供的数据.

[1] 闫姝. 超超临界机组非线性控制模型研究[D]. 北京: 华北电力大学, 2013.

[2] ZHAO Zhenyu, CHEN Yulong, CHANG Ruidong. How to stimulate renewable energy power generation effectively?—China's incentive approaches and lessons[J].RenewableEnergy, 2016, 92: 147-156.

[3] LIU X J, KONG X B, HOU G L, et al. Modeling of a 1 000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods[J].EnergyConversionandManagement, 2013, 65: 518-527.

[4] 马良玉, 高志元. 基于神经网络的超临界机组数学模型[J].动力工程学报, 2013, 33(7): 517-522.

MA Liangyu, GAO Zhiyuan. Mathematical model based on neural network for supercritical unit[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(7): 517-522.

[5] 秦志明, 刘吉臻, 张栾英, 等. 直流炉机组简化非线性动态模型[J].动力工程学报, 2013, 33(12): 955-961.

QIN Zhiming, LIU Jizhen, ZHANG Luanying, et al.A simplified nonlinear dynamic model for once-through boiler units[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(12): 955-961.

[6] 徐蕙, 徐二树. 超超临界1 000 MW机组锅炉动态仿真模型[J].热力发电, 2013, 42(7): 26-31.

XU Hui, XU Ershu. Dynamic simulation model for ultra supercritical 1 000 MW unit boilers[J].ThermalPowerGeneration,2013, 42(7): 26-31.

[7] LIU Jizhen, YAN Shu, ZENG Deliang, et al. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit[J].Energy, 2015, 93: 2069-2078.

[8] SINDAREH-ESFAHANI P, GHAFFARI A, AHMADI P. Thermodynamic modeling based optimization for thermal systems in heat recovery steam generator during cold start-up operation[J].AppliedThermalEngineering, 2014, 69(1/2): 286-296.

[9] CHEN Fafa, TANG Baoping, CHEN Renxiang. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm[J].Measurement, 2013, 46(1): 220-232.

[10] FAN He, ZHANG Yufei, SU Zhigang, et al. A dynamic mathematical model of an ultra-supercritical coal fired once-through boiler-turbine unit[J].AppliedEnergy, 2017, 189: 654-666.

[11] LIN Hongwei, SUN Linjie. Searching globally optimal parameter sequence for defeating Runge phenomenon by immunity genetic algorithm[J].AppliedMathematicsandComputation, 2015, 264: 85-98.

NonlinearDynamicModelofa1 000MWOnce-throughBoilerUnitandItsClosedLoopValidation

FANHe,ZHANGYufei,SUZhigang,WANGPeihong
(Department of Energy Information and Automation, School of Energy and Environment, Southeast University, Nanjing 210096, China)

The method of mechanism analysis was adopted to establish a mathematical model for the coordinated control system of an ultra-supercritical boiler unit over a wide operating range, including the coal pulverizing system, the boiler system and the turbine system, with coal quantity command, total feed water flow and opening degree of turbine valve as the inputs, and with steam enthalpy in separator, main steam pressure and unit power as the outputs. In term of parameter identification, the steady parameters were obtained by non-linear regression analysis combined with steady data; while the dynamic parameters were estimated by immune genetic algorithm (IGA) combined with operation data over a wide operating range. The mechanism model was then validated under both steady and dynamic conditions. Results show that the model owns proper and simple structure, with high accuracy, which therefore may serve as a reference for the testing of control algorithms and the design of CCS.

ultra-supercritical unit; mechanism model; parameter identification; IGA; model validation

2016-09-12

2017-01-22

国家自然科学基金资助项目(51676034)

范 赫(1992-)，男，江苏徐州人，硕士研究生，研究方向为大机组建模与协调系统负荷控制.电话(Tel.):15062265185；E-mail：220140368@seu.edu.cn.

1674-7607(2017)12-0969-08

TK229.2

A

510.80