基于图形表示的减数分裂重组位点识别

张 一, 李雪琴, 李 春

(渤海大学 数理学院, 锦州 121013)

基于图形表示的减数分裂重组位点识别

张 一, 李雪琴, 李 春

(渤海大学 数理学院, 锦州 121013)

减数分裂重组并非以统一的频率发生在基因组上, 而是在某些区域重组频率较高, 在另一些区域重组频率较低。减数分裂重组位点的刻画与识别对于认识重组机制具有重要意义。提出了一种新的DNA序列的3-D图形表示,并将其与Z-曲线相结合,借助正规化的ALE指标,用13维特征向量来刻画DNA序列进而进行减数分裂重组位点识别。以支持向量机作为分类器,利用夹克刀方法进行交互验证,所提方法的总精确度Acc达到了 93.70%,相关系数MCC达到了 0.873。这个结果表明此方法可作为减数分裂重组位点识别领域的一个有力工具。

3-D图形表示；ALE指标；减数分裂重组；支持向量机

减数分裂是发生在有性生殖生物中的一种特殊的细胞分裂过程，减数分裂重组是该过程的重要特征之一。 通过有序形成和修复DNA双链断裂(double-strand break, DSB)的过程, 重组在保留亲本同源片段的同时对等位基因进行重排, 从而增加后代的遗传多样性[1-3]。 全局映射方法已经被用来映像染色体上的DSB位点，从而考察重组区域在基因组上的分布模式。研究表明，减数分裂重组事件并非随机发生，而是具有序列选择性。因此，准确确定重组位点对认识减数分裂重组发生的分子机制以及基因组进化规律具有重要意义。通常，基因组中重组发生频率较高的区域被称为重组热点(recombination hotspot)，而那些重组发生频率较低的区域则被称为重组冷点(recombination coldspot)[1-2,4-6]。 相比之下，重组热点更加引人关注，因为重组频率高，有利于人们记录重组发生的次数和重组过程中的特征[7]。实验是鉴定减数分裂重组冷/热点的最直接的方法,但实验技术自身的缺陷,比如对时间、资金和人力的巨大消耗,使得实验方法难以满足大规模基因组数据处理的实际需求。 所以,发展有效的理论计算方法对减数分裂重组位点进行识别是非常必要的。

对于减数分裂重组冷/热点这样的模式识别问题,如何从DNA序列提取特征是一个非常重要的环节。2013年,Chen等[1]将Chou的拟氨基酸组成与双核苷酸表示相结合构造了19-维特征向量,并将其应用到减数分裂重组位点的识别工作。2014年,Qiu等[2]进一步利用三核苷酸组成以及三联体密码子与氨基酸间的对应关系来提取特征；同年,Li等[4]则考虑了更一般的“拟k-核苷酸组成”构造了96-维向量,并对文献[1-2]中所使用的减数分裂重组位点数据集进行分类,预测结果提高到了84.09%。2016年,Li等[5]基于相位序列和BW转换提取特征并对上述数据集进行分类识别,精度进一步得到了提高。

上述这些方法有一个共同的特点,即都可以归为k-串统计方法，图形表示是DNA序列分析的另一个强有力的工具。1983年,Hamori and Ruskin[8]提出了DNA序列的H-曲线,这是DNA序列图形表示方面较早的工作。1994年,Zhang等[9]提出了DNA序列的Z曲线，2000年,Randic等[10]将Gates[11], Nandy[12]， Leong和Morgenthaler[13]等2维平面图形表示推广到3维空间。 受Randic等[10]的启发,我们提出了DNA序列的一种新的3-D图形表示方法,并将其与Z曲线相集合,利用我们在文献[14]中提出的ALE指标构造了DNA序列的13维向量表示。以支持向量机作为分类器,我们对文献[1-2,4-5]所用的数据集进行分类预测，通过夹克刀交叉验证,我们所提方法的识别率达到了93.70%。

1 数据集

本文所涉及的数据来自于文献[1-2]，该数据集共包含1081 条 DNA序列,为方便起见,本文称之为“数据集1081”。其中,490 条为减数分裂重组热点序列,它们构成正样本集；另外的 591 条为减数分裂重组冷点序列,它们构成负样本集。

2 新的DNA序列3-D图形表示

对于4种核苷酸碱基A,C,G,T现在分别赋予它们4个三维空间中的向量：

A=(2,-1,0),C=(1,0,2),G=(-1,-2,0),T=(-2,0,1)

假设S=S1S2S3…SK是一条给定的DNA序列。从第一个碱基开始依次考察此序列的每一个碱基,对于第i个碱基(i=1,2,…,K),可以由下列公式得到一个三维空间的点Qi(li,mi,ni)

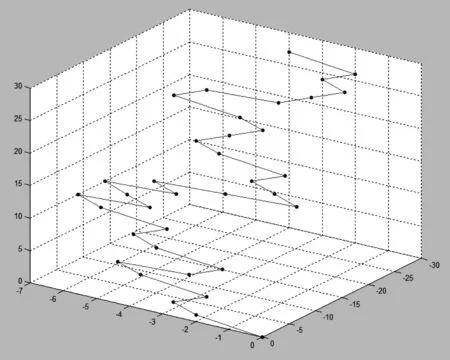
图1 序列S的3-D图形表示

上述3-D图形表示具有如下性质：

性质：3-D图形表示不存在圈,即非退化。

证明：假设：1)曲线中任意圈的长度为n;2)该圈中A,C,G,T的数目分别为Ak,Ck,Gk,Tk,则Ak+Ck+Gk+Tk=n。

由于Ak个A,Ck个C,Gk个G，Tk个T可以构成一个圈,所以有Ak(2,-1,0)+Ck(1,0,2)+Gk(-1,-2,0)+Tk(-2,0,1)=0,即

解得Ak=Ck=Gk=Tk=0,进而,n=0， 即圈长为0。

需要指出的是,上述图形表示是在三维空间中,将4个向量(2,-1,0), (1,0,2), (-1,-2,0)和(-2,0,1)分别赋予4个碱基A,C,G,T而得到的。如果改为将向量(2,-1,0), (1,0,2), (-1,-2,0)和(-2,0,1)分别赋予碱基A,T,G,C,则将得到另一条3-D曲线。不难发现,通过将这样的4个向量赋予4个碱基,由一条DNA序列可以得到12种本质上不同的3-D曲线。

3 DNA序列的数值刻画

图形表示作为一种可视化工具,为挖掘DNA原始序列信息提供了一种定性的研究方法。与之对应,数值刻画则提供了一种定量地分析DNA序列的方法。对于如上每一条3-D曲线,这里构造其L/L矩阵。L/L矩阵定义如下[15-16]：

其中d(i,j)是曲线上两点vi,vj之间的欧式距离。

一旦DNA序列的矩阵形式给出后,就可以通过矩阵不变量来刻画这个DNA序列。 文献中常用的矩阵不变量有：Wiener数、平均矩阵元素、平均行和与平均列和、最大特征值等。其中,最大特征值可以很好地反映出矩阵的有关信息并在化学和生命科学等领域得到了广泛应用[10,14-18]。 然而,随着矩阵阶的增加,特征值的计算会变得越来越困难。 为了克服这个问题,Li和Wang[14]在2005年提出了ALE指标， ALE指标可视为相应矩阵最大特征值的一个近似值,但它的计算要比最大特征值容易得多。 因此这里采用的不变量是ALE指标,其定义如下：

其中n为矩阵的阶, ‖·‖m1和‖·‖F为矩阵的m1-范数和F-范数。为了避免不同矩阵大小不同造成的影响,可以考虑使用正规化的ALE指标χ/n来作为矩阵不变量。于是,与上述12条3-D曲线相对应,可以得到12个正规化的ALE指标。

此外, Z-曲线是张春霆等早在1994年提出的一种DNA序列3-D图形表示。其三维空间中点与相应序列片段中碱基出现的个数An,Cn,Gn,Tn之间的对应关系如下[9]：

Z-曲线和本文提出的3-D曲线是从不同角度对DNA序列进行图形表示的。一条DNA序列的Z-曲线中可能会出现圈,但它能突显嘌呤/嘧啶、氨基/酮基、弱氢键/强氢键之间的关系。 在某种意义上讲,二者能够相互补充。 基于这一点,本文应用相同的方法计算Z-曲线的正规化的ALE指标。

最终,本文采用由上述13个正规化的ALE指标构成的13维向量VALE=(v1,…,v12,v13)来刻画DNA序列。 其中,v1～v12是本文提出的3-D曲线对应的12个ALE指标,v13是Z-曲线对应的ALE指标。 例如, 序列S=ATGCTGACTGCTGAGGAGAAGGCTGCCGTCACCGCT的13维向量为：

VALE=(0.5786,0.5870,0.5819,0.5550,0.5377,0.5736,0.6118,0.6020,0.5957,0.5350,0.5435,0.5938,0.3763)

5 分类器的选择及其预测性能的评估

在机器学习和模式识别领域,支持向量机(SVM)作为一个很有效的机器学习方法被广泛使用。 本文将选择SVM作为分类器,并利用LIBSVM(http://www.csie.ntu.edu.tw/～cjlin/libsvm/)软件包来执行SVM分类。

表1是两类数据的混合矩阵,它是二分类问题中预测评价分类性能的常用模型。

表1 两类数据的混合矩阵

其中,TP和TN分别表示分类正确的正类数据和负类数据的个数,FP和FN分别表示分类错误的正类数据和负类数据的个数。本文采用敏感度(Sn)、特异性(Sp)、准确度(Acc)和相关系数(Mcc)这4个文献中常用的指标来评价我们方法的预测性能。这些指标的定义如下[19]。

1)敏感度(Sn)：敏感度表示的是分类正确的正类样本个数与正类测试集大小的比值,即

2)特异性(Sp)：特异性表示的是分类正确的负类样本个数与负类测试集大小的比值,即

3)准确度(Acc)：准确度表示的是分类正确的样本个数与测试集大小的比值,即

4)相关系数(Mcc)：相关系数表示的是正负测试集比率的一个平衡,可表示为

从定义的形式上可以看出： Acc 及 Mcc的值越大,说明预测总精度越高,且两类预测正确的样本个数都达到了一个较为理想的水平,相应分类性能也就越好。

5 结果与讨论

对于数据集1081中的每条序列,我们首先将其转化为一个13维特征向量,然后将这1081个向量规范化后输入到支持向量机中。本文采用径向基核函数方法,并利用LIBSVM软件包中的grid搜索策略,获得最优参数对(C=32 768,g=2.0)。众所周知,在几种交互验证方法中,夹克刀方法被认为是最有效的[1-2,4-5,19],所以本文采用夹克刀法进行交互验证。结果发现TP=454,FN=36,TN=559,FP=32，从而得到敏感度Sn=92.65%,特异性Sp=94.58%,准确度Acc=93.70%,相关系数Mcc=0.873(见表2)。为了方便比较,本文将近年来针对同一数据集1081并使用夹克刀进行预测的结果也列在表2。

表2 与现有的方法进行比较

[a]取自Li等[5]；[b] 取自Li等[4]；[c] 取自Qiu等[2]；[d] 取自Chen等[1]

从表2可以看出：我们提出的方法的Sn比其他4种方法高出5.51%～22.24%,Sp比其他4种方法高出3.89%～14.99%,Acc比其他4种方法高出8.78%～13.31%,Mcc比其他4种方法高出0.178～0.268。这个结果表明我们所提方法可视为减数分裂重组位点识别领域的一个有用的工具。

6 结论

通过将4个三维空间中的向量(2,-1,0),(1,0,2),(-1,-2,0),(-2,0,1)赋予4种核苷酸碱基,本文提出了一种新的DNA序列的3-D图形表示。进一步,将其与Z-曲线相结合,借助正规化的ALE指标,用13维特征向量来刻画DNA序列并进行减数分裂的重组位点识别。本文以支持向量机作为分类器,利用夹克刀方法进行交互验证。与现有方法相比,本文所提方法在敏感度、特异性、准确度和相关系数这4个指标上均有较明显的提高。

[1]CHEN W, FENG P M, LIN H, et al. iRSpot-PseDNC: identify recombination spots with pseudo dinucleotide composition[J]. Nucleic Acids Research, 2013, 41(6): e68.

[2]QIU W R, XIAO X, CHOU K C. iRSpot-TNCPseAAC: identify recombination sports with trinucleotide composition and pseudo amino acid components[J]. Molecular Sciences, 2014, 15(2): 1746-1766.

[3]孙晓光. 粗糙脉胞菌减数分裂重组和突变的研究[D]. 南京：南京大学, 2016.

[4]LI L Q, YU S J, XIAO W D, et al. Sequence-based identification of recombination spots using pseudo nucleic acid representation and recursive feature extraction by linear kernel SVM[J]. BMC Bioinformatics, 2014, 15: 340-358.

[5]LI C, HAN M M, YANG Y, et al. Identification of meiotic recombination spots based on phase-specific sequence and Burrows Wheeler transform[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13(7): 4131-4135.

[6]张冰洁. 减数分裂重组对DNA序列和染色质结构的依赖性[D]. 包头：内蒙古科技大学, 2013.

[7]高 玲, 慕小倩, 林 煜, 等. 真核生物减数分裂重组热点的研究进展[J]. 遗传, 2005, 27 (4): 641-650.

[8]HAMORI E, RUSKIN J. H curves, a novel method of representation of nucleotide series especially suited for long DNA sequences [J]. Journal of Biological Chemistry, 1983, 258 (2): 1318-1327.

[9]ZHANG R, ZHANG C T. Z curves, an intuitive tool for visualizing and analyzing DNA sequences [J]. Journal of Biomoecular Structure and Dynamics, 1994, 11 (4): 767-782.

[10]RANDIC M, VRACKO M, NANDY A, et al. On 3-D graphical representation of DNA primary sequences and their numerical characterization [J]. Chem Inf Comput Sci， 2000, 40 (5): 1235-1244.

[11]GATES M A. A simple way to look at DNA [J]. Journal of Theoretical Biology, 1986, 119 (3): 319-328.

[12]NANDY A. Graphical representation of long DNA sequences [J]. Current Science, 1994, 66: 821.

[13]LEONG P M, MORGENTHALER S. Random walk and gap plots of DNA sequences [J]. Computer Applications in the Biosciences, 1995, 11 (5): 503-507.

[14]LI C, WANG J. New invariant of DNA sequences [J]. Journal of Chemical Information and Modeling, 2005, 45: 115-120.

[15]LI C, LI X Q, LIN Y X. Numerical characterization of protein sequences based on the generalized Chou′s pseudo amino acid composition[J]. Appl Sci， 2016, 6 (12): 406.

[16]RANDIC M, VRACKO M, LERN, et al. Analysis of similarity/dissimilarity of DNA sequences based on novel 2-D graphical representation[J]. Chem Phys Lett， 2003, 371: 202-207.

[17]RANDIC M, GUO X F, BASAK S C. On the characterization of DNA primary sequences by triplet of nucleic acid bases[J]. J Chem Inf Comput Sci， 2001, 41(3): 619-626.

[18]RANDIC M, NOVIC M, VRACKO M, et al. Study of proteome maps using partial ordering[J]. Journal of Theoretical Biology, 2010, 266(1):21-28.

[19]YU X Q, GAO H Y, ZHENG X Q, et al. A computational method of predicting regulatory interactions in Arabidopsis based on gene expression data and sequence information[J]. Computational Biology and Chemistry, 2014, 51: 36-41.

Identificationofmeioticrecombinationspotsbasedonthegraphicalrepresentation

ZHANG Yi, LI Xue-qin, LI Chun

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

The meiotic recombination events do not occur with a uniform frequency throughout the genome but with a higher rate in some regions and lower in others. Characterization and identification of meiotic recombination spots is critical for our understanding of the recombination mechanism. In this paper, we first propose a new 3-D graphical representation for a DNA sequences. Then, combining the 3-D graphical representaion with Z-curve, we characterize a DNA sequence by a 13-D vector whose components are the corresponding normalized ALE indices. Support vector machine (SVM) and Jackknife cross-validation test are employed to perform our method on a benchmark dataset for recombination spots. Results show that our method achieved an overall accuracy of 93.70% with the Matthew′s correlation coefficient (MCC) of 0.873, which suggests that the proposed method can serve as a useful tool for identifying the recombination spots.

3-D graphical representation; ALE-index; meiotic recombination; support vector machine

2016-12-20；

2017-01-20

辽宁省自然科学基金项目(201602005)；辽宁省高等学校创新团队(LT2014024)；辽宁省食品安全重点实验室开放课题(LNSAKF2011034)

张 一,硕士,主要研究方向为计算分子生物学,E-mail：798332334@qq.com

李 春,博士,教授,主要研究方向为食品安全与生物信息学，E-mail：lichwun@163.com

10.3969/j.issn.2095-1736.2017.06.101

Q71

B

2095-1736(2017)06-0101-04