采用振动信号二维特征向量聚类的配电开关机械状态识别新方法

高 伟， 杨耿杰， 郭谋发， 徐丽兰， 陈永往

(1. 福州大学电气工程与自动化学院， 福建 福州 350116； 2. 国网福建漳州市供电有限公司， 福建 漳州 363000；3. 国网福建晋江市供电有限公司， 福建 泉州 362200)

采用振动信号二维特征向量聚类的配电开关机械状态识别新方法

高 伟1， 杨耿杰1， 郭谋发1， 徐丽兰2， 陈永往3

(1. 福州大学电气工程与自动化学院， 福建 福州 350116； 2. 国网福建漳州市供电有限公司， 福建 漳州 363000；3. 国网福建晋江市供电有限公司， 福建 泉州 362200)

配电开关动作产生的振动信号具有非线性非平稳特性， 蕴含机械状态信息. 提出一种基于振动信号二维特征向量和模糊K均值聚类的配电开关机械状态识别新方法. 利用HHT带通滤波对配电开关振动信号进行时频分解， 分别求取各子频带信号的能量值和重心频率， 得到振动信号的二维特征向量作为反映配电开关的机械状态的特征量. 提取配电开关在正常、 底座螺丝松动、 机械结构卡涩及卸掉A相触头绝缘拉杆等4种典型状态实测振动信号的二维特征向量做模糊K均值聚类， 结果表明， 所提取的特征向量能有效地表征配电开关的机械状态.

配电开关； 机械状态； 振动信号； 二维特征向量； HHT带通滤波； 模糊K均值聚类

0 引言

开关电气故障如触头接触不良等， 大多由操作机构失灵、 切换不到位等机械故障引起[1]. 统计表明， 约80%的开关故障由机械特性不良所造成[2-3]. 对开关常见的机械故障状态如机械结构卡涩、 弹簧或螺丝松动等进行监测、 诊断， 可为开关设备状态检修提供有效的状态量.

开关动作所产生的振动信号蕴含有机械状态信息， 机械状态的改变将导致振动信号的变化， 利用振动信号进行高压断路器机械故障诊断的研究由来已久[3-6]. 一般利用振动信号的有效特征量识别机械状态， 而开关振动信号具有非周期、 非平稳变化特点， 如何提取振动信号的有效特征量对开关机械故障诊断至关重要. 已有文献大多在振动信号的幅值上提取其特征量， 如频谱熵、 时频能量熵等[7-10]， 这些特征量实质上均为一维信息， 仅反映振动信号能量集中程度， 无法反映其能量集中的位置， 具有一定的局限性. 另外， 针对配电开关设备的相关研究文献较少.

提取振动信号能量及其重心频率作为其特征量， 提出一种基于振动信号二维特征向量模糊聚类的配电开关机械状态识别新方法. 对振动信号作HHT带通滤波， 提取振动信号的能量、 重心频率等二维特征向量. 该向量可同时反映振动信号能量集中程度及能量集中位置， 较为全面地刻画了振动信号的时频特征. 利用模糊K均值聚类(FKM)[11]实现配电开关不同机械状态的识别. 对中压SF6绝缘环网负荷开关模拟常见的机械故障， 测取相应的振动信号， 分析结果表明, 该方法能有效地识别配电开关的不同机械状态.

1 配电开关振动信号的时频分解方法

希尔伯特-黄变换(简称HHT)是一种具有完全自适应性的时频分析算法， 包括经验模态分解(简称EMD)和Hilbert变换, 适合于分析非周期非平稳信号[3， 12-14]. HHT需考虑采样频率、 数据窗、 边界条件及模态混叠等问题. EMD的模态混叠与信号的频率特性和EMD算法本身有关. 正态分布的白噪声经EMD后， 信号内均匀分布的各频率被规则地分解到各阶IMF内， 且前一阶IMF的频率是后一阶IMF的两倍， EMD类似于一个有效的二进制滤波器组. 人为地在原始信号中加入正态分布的白噪声， 可使混合信号的尺度均匀分布在时频空间内， 有效消除EMD产生的模态混叠现象. 基于此， Huang等[15]提出了集合经验模态分解的方法， 通过将信号预白化， 提高HHT分析的准确性.

配电开关动作信号经集合经验模态分解后， 得到各阶固有模态函数(简称IMF)分量， 提取各阶IMF分量中所有同频率点的瞬时值进行重构， 可得到原始振动信号的某个频率分量. 通过带通滤波亦可重构出不同频带内的原始振动信号分量， 该滤波方法称为HHT带通滤波[3， 16-17]. 其步骤如下：

1) 对配电开关振动信号进行集合经验模态分解， 得到各阶IMF分量和趋势分量.

2) 求各阶IMF分量的Hilbert时频谱， 得到各阶IMF分量所对应的瞬时频率.

3) 逐次对每阶IMF分量的瞬时频率进行判断， 若此频率不在选定频带的范围内， 则将此时刻对应的IMF分量置零.

4) 将经处理后的各阶IMF分量累加， 得到选定频带范围内的振动信号分量.

5) 继续求得振动信号在其他频带内的分量.

2 配电开关振动信号二维特征向量求取方法

设一维振动信号时间序列{x(n)|n=1, 2, …,N}， 以Δf为平均带宽， 经一次HHT带通滤波重构得L个子频带分量； 每个子频带分量， 以Δf′为平均带宽， 进行二次HHT带通滤波得M个二次重构分量. 其中:L等于振动信号的频带范围与一次HHT带通滤波带宽的比值，M等于一、 二次HHT带通滤波的带宽比值. 再分别按下列算式求得能量值和重心频率.

由于各个特征值的幅值大小不一， 为便于各振动信号的特征向量进行比较， 对能量和重心频率作归一化处理， 转换为无单位的值.

将这k个振动信号的能量值和重心频率按下式组合成一个新矩阵Ef作为配电开关机械状态二维特征向量矩阵. 每一行代表一个振动信号的特征， 每两列组成该振动信号一个频段的二维特征， 由此构成k×2L的矩阵. 由于同时反映了配电开关振动信号能量值大小和重心频率的变化， 二者互为补充， 相比于用一维特征量表征配电开关振动信号， 二维特征向量可更好地体现振动信号的时频分布特征.

图1 振动信号二维特征向量提取算法流程框图 Fig.1 Extracting flow of 2-D feature vector

振动信号的二维特征向量与开关操作振动模式有关， 当振动模式相对稳定时， 分解后的二维特征向量较为接近； 若检测到的二维特征向量与正常状态下出现较大偏差， 表明该开关的振动模式发生了变化， 机械状态可能出现异常[3].k个振动信号二维特征向量提取算法流程如图1所示.

3 配电开关振动信号检测及特征量提取

3.1 配电开关振动信号检测

配电开关状态检测系统由加速度传感器、 信号采集装置和信号分析软件组成， 如图2所示. 加速度传感器的频率响应范围为0.5～6 000 Hz， 灵敏度为100 mV·(m·s-2)-1， 量程为50 m·s-2， 满量程时输出电压为5 V； 信号采集装置由NI的数据采集模块6211搭建， 信号分析软件采用Matlab和LabVIEW开发. 对中压SF6负荷开关动作进行实验， 加速度传感器安装在最靠近振动源的开关操动机构主轴附近， 如图3所示. 检测配电开关在正常状态、 底座螺丝松动、 机械结构卡涩及卸掉A相触头绝缘拉杆等情况下的大量合闸振动信号， 振动信号幅值为加速度传感器输出电压值的大小.

图2 振动信号检测系统 图3 加速度传感器安装位置Fig.2 Vibration signal detection system Fig.3 Installation location of acceleration sensor

3.2 配电开关振动信号二维特征量提取

当开关发生分合闸操作， 振动信号出现急剧变化， 为消除传感器零漂影响， 设定启动阈值为3.3 V. 信号幅值超过阈值时， 截取启动前后0.1 s(其中启动前7.5 ms)时长的振动信号， 作为待分析信号. 由文[3]可知， 信号频率主要分布在0～20 kHz范围. 对截取的信号做集合经验模态分解， 并以2 kHz带宽将信号划分成10个频带， 通过HHT带通滤波进行一次重构， 得到10个子频带的重构分量. 对一次重构分量再进行二次HHT带通滤波， 取二次带通滤波的频带宽度为0.4 kHz， 则每个子频带重构分量可得到5个二次带通滤波重构分量， 由这5个二次带通滤波重构波形可提取1个能量值和1个重心频率， 将其作为各二次重构分量的二维特征向量， 则1个振动信号可提取10个二维特征向量. 对配电开关在底座螺丝松动和卸掉A相触头绝缘拉杆等情况下的合闸振动信号各取3组数据， 提取其二维特征向量， 可得图4所示的分布图， 6组数据的二维特征向量通过不同颜色或符号加以区别.

图4 二维特征向量分布图Fig.4 Scattergram of 2-D feature vector

由图4可看出， 配电开关底座螺丝松动和卸掉A相触头绝缘拉杆这两种机械故障状态的二维特征在低频部分能量较大， 高频部分能量较小， 接近于零； 在第1、 6、 7、 8、 9重构频带能量差异明显， 第2重构频带重心频率差异明显. 二维特征向量不仅反映了配电开关振动信号的能量集中程度， 同时直观反映了其能量集中的位置， 两者互相补充， 可较为全面地描述信号时频特征的变化情况.

为识别配电开关在正常状态、 底座螺丝松动、 机械结构卡涩及卸掉A相触头绝缘拉杆等4种情况下的振动信号， 每种状态各取3组作为样本， 再取2组任意状态数据作为待检数据. 编号如下： 1～3为正常状态， 4～6为底座螺丝松动， 7～9为机械结构卡涩， 10～12为卸掉A相触头绝缘拉杆， 13～14为测试数据. 求取这14组数据的能量值El和重心频率Fg， 分别如下所示.

4 基于FKM聚类的配电开关机械状态识别

4.1 FKM聚类

模糊聚类算法常用于开关振动信号特征量识别， 其中多采用模糊C均值聚类(fuzzy C-mean, FCM)， 识别效果较好[18-19]. 但FCM在应用中存在一些不足， 如算法对初值敏感， 不同的初值可能得到不同的聚类结果， 甚至无解.

模糊K均值聚类[11]是一种基于模糊划分、 非监督动态聚类方法， 相比于FCM聚类， 该算法可人为输入将待分类的n个向量xj(j=1, 2, …,n)分成k类的初始模糊隶属度矩阵U(1)， 弥补了FCM的不足.

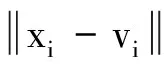
4.2 配电开关机械状态识别

将振动信号的二维特征向量表征配电开关振动模式， 并通过逐步建立相应的振动指纹库， 为配电开关机械故障诊断奠定基础. 通过对正常状态、 底座螺丝松动、 机械结构卡涩和卸掉A相触头绝缘拉杆等4种情况下开关合闸振动信号二维特征向量的FKM聚类识别， 验证本文所提方法的有效性.

将式(6)、 式(7)按式(5)组合成一个新矩阵Ef, 将Ef作为FKM聚类的输入， 已知样本状态有4种， 设置FKM聚类数目为4， 初始模糊隶属度矩阵U(1)如下式所示：

其中： 各已知状态的隶属度均取0.7， 表示对应状态已知， 而待验状态1、 2的隶属度取0.1， 表示对应状态未知. 取加权指数m=2， 迭代中止因子ε=10-5， 最大迭代次数kmax=100. 迭代收敛后， 得到隶属度矩阵如下式所示.

表1 FKM分类结果Tab.1 Classification results of FKM

U为4×14的矩阵， 行号对应状态类别， 列号对应样本编号，U中的元素表征每个样本属于相应状态类别的隶属度， 隶属度越大属于该状态类别的概率越高. 根据U中元素最大值出现的位置获得表1的分类结果： 样本1～3同属一类， 为正常状态； 10～12同属一类， 为底座螺丝松动状态； 待验样本13和样本4～6同属一类， 判别为底座螺丝松动状态； 待验样本14与样本7～9同属一类， 判别为机械结构卡涩状态， 以上判定结果和实际状态一致.

5 结语

1) 由振动信号的能量及重心频率构成其时频二维特征向量， 两者互相补充， 可较为全面地描述信号时频特征的变化.

2) 通过两次HHT带通滤波， 每个振动信号均得到多个二维特征向量， 该向量可更有效地反映振动信号的复杂特性.

3) 不同机械故障类型振动信号的FKM聚类识别验证了振动信号二维特征向量的有效性， 为配电开关机械故障诊断指纹库的建立提供了一种有效手段.

[1] 赵彤， 李庆民， 陈平. OLTC振动信号特征提取的动力学分析方法[J]. 电工技术学报， 2007， 22(1)： 41-46.

[2] 杨凌霄， 朱亚丽. 基于概率神经网络的高压断路器故障诊断[J]. 电力系统保护与控制， 2015， 43(10): 62-67.

[3] 郭谋发， 徐丽兰， 缪希仁， 等. 采用时频矩阵奇异值分解的配电开关振动信号特征量提取方法[J]. 中国电机工程学报， 2014， 34(28)： 4 990-4 997.

[4] 常广， 王毅， 王玮. 采用振动信号零相位滤波时频熵的高压断路器机械故障诊断[J]. 中国电机工程学报， 2013， 33(3)： 155-162.

[5] 黄建， 胡晓光， 巩玉楠. 基于经验模态分解的高压断路器机械故障诊断方法[J]. 中国电机工程学报， 2011， 31(12)： 108-113.

[6] 孙来军， 胡晓光， 纪延超. 一种基于振动信号的高压断路器故障诊断新方法[J]. 中国电机工程学报， 2006， 26(6)： 157-161.

[7] 彭文季， 罗兴锜. 基于小波包分析和支持向量机的水电机组振动故障诊断研究[J]. 中国电机工程学报， 2006， 36(24)： 164-168.

[8] 庞尔军， 王晓龙， 于虹. 基于虚拟仪器技术的振动测试分析系统[J]. 机床与液压， 2014， 42(7)： 171-173.

[9] 李斌， 李爽， 鲁旭臣. 高压断路器机械特性振动信号特征提取和故障诊断方法研究[J]. 高压电器， 2015， 51(10): 138-144.

[10] 周翔， 王丰华， 傅坚， 等. 基于混沌理论和K-means聚类的有载分接开关机械状态监测[J]. 中国电机工程学报， 2015， 35(6)： 1 541-1 548.

[11] 周宏伟， 周玉光， 关添升， 等. 基于模糊k均值的变压器分接开关故障诊断[J]. 吉林大学学报(信息科学版)， 2015， 33(6): 719-722.

[12] HUANG N E， SHEN Z， LONG S R，etal. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences， 1998， 454(1 971)： 903-995.

[13] VINCENT H T， HU S J， HOU Z. Damage detection using empirical mode decomposition method and a comparison with wavelet analysis[C]// Proceedings of the Second International Workshop on Structure Health Monitoring. California: Stanford University， 1999： 891-900.

[14] HUANG N E， SHEN Z， LONG S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics， 1999， 31(1)： 417-457.

[15] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[16] 郭谋发， 刘世丹， 杨耿杰. 采用Hilbert谱带通滤波和暂态波形识别的谐振接地系统故障选线新方法[J]. 电工电能新技术， 2013， 32(3)： 67-74.

[17] 李建鹏， 赵书涛， 夏燕青. 基于双谱和希尔伯特-黄变换的断路器故障诊断方法[J]. 电力自动化设备， 2013， 33(2): 115-119； 125.

[18] 梅飞， 梅军， 郑建勇， 等. 粒子群优化的KFCM及SVM诊断模型在断路器故障诊断中的应用[J]. 中国电机工程学报， 2013， 33(36)： 134-141.

[19] 刘长良， 武英杰， 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报， 2015， 35(13)： 3 358-3 365.

Anovelmechanicalstateidentificationmethodfordistributionswitchbasedonvibrationsignal2-Dfeaturevectorwithclusteringalgorithm

GAO Wei1， YANG Gengjie1， GUO Moufa1， XU Lilan2， CHEN Yongwang3

(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China；2. State Grid Fujian Zhangzhou County Electric Power Supply Co. Ltd., Zhangzhou, Fujian 363000, China；3. State Grid Fujian Jinjiang County Electric Power Supply Co. Ltd., Quanzhou, Fujian 362200, China)

Vibration signals of distribution switches that contain mechanical information are characterized by nonlinearity and nonstationarity. Thus, A novel mechanical state identification method for distribution switch based on vibration signal 2-D feature vector with fuzzy K-mean clustering algorithm was proposed in this paper. Taking advantage of HHT band-pass filter, vibration signals would be decomposed in time and frequency domain in order to obtain each sub-band reconstructed signal’s energy and center frequency as the 2-D feature vector, which could represent the mechanical state for distribution switch. FKM clustering was applied to these 2-D feature vectors of observed vibration signals in four typical conditions including normal states, screw loosing states， mechanical structure clamping stagnation states and relieved insulated pull rod of phase A contacts states. Results show that the feature quantity can represent the mechanical state of distribution switch accurately and effectively.

distribution switch; mechanical state; vibration signal; 2-D feature vector; HHT band-pass filter; FKM clustering

10.7631/issn.1000-2243.2017.05.0674

1000-2243(2017)05-0674-07

TM77

A

2016-04-12

杨耿杰(1966-)， 教授， 主要从事电力系统分析研究， 80201931@qq.com

福建省自然科学基金资助项目(2016J01218)； 福建省教育厅科研资助项目(JA15086)

(责任编辑： 沈芸)