基于软件定义网络的多路径路由算法性能研究

傅明建， 吴 凡， 黄芳芳， 郭龙坤

(1. 福州大学网络信息安全与计算机技术国家级实验教学示范中心, 福建 福州 350116；2. 福州大学数学与计算机科学学院， 福建 福州 350116； 3. 国网福建省电力有限公司信息通信分公司， 福建 福州 350003)

基于软件定义网络的多路径路由算法性能研究

傅明建1， 2， 吴 凡2， 黄芳芳3， 郭龙坤2

(1. 福州大学网络信息安全与计算机技术国家级实验教学示范中心, 福建 福州 350116；2. 福州大学数学与计算机科学学院， 福建 福州 350116； 3. 国网福建省电力有限公司信息通信分公司， 福建 福州 350003)

基于不相交多路径的路由方案在负载平衡、 容错等方面具有明显优势， 但存在计算复杂度高的缺点， 故对应的分布式算法难以在网络中大规模部署. 通过分析软件定义网络的特点， 论证了在其网络中部署不相交路径路由方案的可行性. 其次， 基于网络流的性质与不相交路径的图论性质， 设计并实现了计算不相交路径的算法. 最后， 通过一系列基于不同网络模型的对比实验， 验证所提算法较传统最短单条路径路由算法具有更佳的负载均衡. 实验结果表明, 该算法的性能与网络中链路能承受的负载极限阈值有关.

软件定义网络； 不相交多路径路由； 负载均衡

0 引言

随着互联网的迅速发展， 无论在交通运输、 大众媒体和电力行业等传统领域， 还是在大数据技术、 云计算和智慧城市等新兴领域， 如何最小化所占用的网络资源来提高网络的可靠性都是科研的热点课题. 当前的多路径路由算法大都基于部分不相交多路径， 主要应用于无线传感网等具有中心控制器的网络中. 这些已实现的多路径路由具有如下特点： 1) 对于不同的服务质量要求， 可通过结合对应网络的各种情况，提供不相同的路径； 2) 对类似的服务寻找并给出多条路径， 共用这些不同的路径可达到满意的服务质量； 3) 因为总体拥有所有路径的有效使用权， 它将会以各条路径的具体情况(丢包率)为依据， 假想网络的拥塞程度， 再统筹各条路径的占用， 最终不仅保证优质服务， 还能增加网络的总体利用率. 总体而言， 这些已有的路由方法通过合理共用多条通路， 改善了网络的负载均衡， 提高了整个网络的总体利用率.

理论上， 多路径路由具有更好性能是因为其并非使用最优路径， 而是使用多条次优路径. 依照次优选择理论[1]， 使用多条次优路径， 相较于使用少数几条次优路径(通常由网络拥塞引起的最优路由转为次优路径)， 并不会有太大的性能降低. 对比最短路径路由, 多路径路由通常可以为网络参与博弈的多方提供更好的路由方案. 依照网络流理论， 不相交路径相比于部分不相交路径可提供更大的网络流[2]. 因此， 不相交路径路由理论上应具有更好的网络负载均衡， 更有利于提高网络的总体利用率. 本研究将针对不相交的多路径路由展开讨论.

然而， 由于不相交路径路由方案的计算复杂度高， 对应的分布式算法难以实现， 使得不相交路径路由方案在网络中不能得到大规模部署. 虽然对于计算多条不相交路径已存在可并行化的高效算法[3]， 但却不存在高效的对应分布式算法. 近十年来， 网络研究者逐渐设计出一系列关于不相交路径(特别是QoS约束不相交路径)的高效算法[4-6]. 如今， 在软件定义网络(software defined networking， SDN)中利用中心控制器能够解耦对路径的依赖， 从而实现数据控制分离且接口统一的架构. 软件定义网络架构的主要思想是通过控制功能与数据平面的分离理念， 完成了对网络的可编程管理， 使得对控制网络的集中化、 精准化变得更为方便[7]. 软件定义网络架构包含了基础设施层、 控制层和应用层. 在该架构中， 传统的交换机不再具有控制能力， 转而由控制层来控制. 基础设施层和控制层之间添加了标准接口以保证交换机能够实现对转发数据的识别[8-12]. 控制层会将设备的分布状态抽象成为全网视图. 而应用层通过分析各个网络应用在需求上的差异， 找到并调用与控制层相连的应用编程接口(API)， 最终实现不同应用程序的功能. 通过API接口， 业务应用得以利用网络的服务和能力， 在抽象的网络上操作， 从而实现路由、 带宽管理、 服务质量、 访问控制等网络服务[13-14].

本研究以软件定义网络为背景， 实现并验证了不相交多路径路由算法在负载均衡上的表现. 选取了完全图、 网格图和X网格图作为网络模型， 设计实验比较单路径和多路径路由的区别， 并通过比较两种路由方式的负载协方差， 验证了不相交多路径路由算法在负载均衡上的优势. 此外， 通过实验发现了算法性能与链路的负载能力， 即其能承受的负载极限阈值.

1 问题描述

链路不相交的多路径不能简单使用多遍Flody函数计算得出[15]. 本研究将通过一个双路径最短路径的例子阐述该观点. 如图1所示， 这是一个4个节点间的完全图， 路径长度图中已标出. 简单调用Flody算法(或其它类似最短路径的方法)找出a到d之间的不相交最短路径的过程如下： 找到第一条路径a-b-c-d作为单路径最短路径， 路径长度为3； 由于路径不相交， 那么找出的第二条路径a-d长度为8， 多路径总长度为11. 但是该解并不是最优解.

为了有效解决这一问题， 本研究通过以下方法进行优化： 在找到第一条路径a-b-c-d的前提下， 将第一条路径取反， 也就是只允许反向通路, 如图2所示.

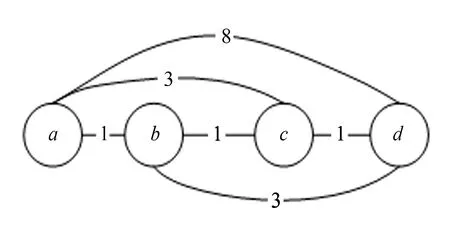
图1 4节点完全图Fig.1 4 Nodescomplete graph

图2 反向优化后的4节点完全图Fig.2 4 Nodescomplete graph after reverse optimization

此时再调用Flody函数就可以找到正确的第二条最短路径， 这里a-c-b-d路径长度为7小于a-d长度为8的路径. 在找到两条路径后， 还需要将这两条路径进行整合优化， 得出正确的不相交多路径最短路径. 此时的两条路径为a-b-c-d和a-c-b-d， 显然， 中间的b-c路径正反向均有路径走过， 根据循环相消原理， 可以得到最终的最短双路径为a-c-d和a-b-d， 且多路径总长度为8， 为最优解(如图2所示). 对于路径条数大于2的多路径最短路径的寻找方法， 原理与其完全相同， 只需要将找到的双路径最短路径全部取反， 然后在得到的新图上调用Flody函数找到第3条最短路径， 再结合之前的2条路径， 通过循环相消原理进行整合优化， 便可得出多路径最短路径(该算法的设计将在第二节进行详细阐述). 上述算法的思想来源于网络流的计算算法： 首先将多条不相交路径视为一个从源结点到终端结点的网络流； 然后通过修改网络流的算法以计算不相交路径.

2 不相交多路径路由算法的设计与实现

2.1 输入

为了使实验具有可靠性和普遍性， 本研究将路由数量取为非质数， 这样利于数据的输入和调配工作. 首先将不规则的路由网络抽象规则化， 以x×y的形式按顺序排列成以x为长，y为宽的长方形点阵， 例如由3×3的9个路由组成的辅助样例图.

2.2 图的分类

1) 完全图. 假定每一个路由间都应该有且仅有一条路， 而当这些路全部为通路时， 将得到的是一张完全图. 如果模型大小为N×N， 则共有(N2×(N2-1))/2条路径. 因此， 在这类完全图代表的网络模型中， 任意一个路由都与其它所有路由间存在通路. 虽然这种情况太过于理想化， 不太贴合实际网络情况， 但是将其作为模型进行试验也具有一定的研究价值， 因此本研究将其考虑在内.

2) 网格(Mesh)图. 在实际情况中存在这样一种路由模型， 网络上的路由仅与其相邻的四个正方向上的路由存在通路. 在网格模型中， 如果模型大小为N×N, 则共有2N×(N-1)条路径. 当N=3时， 此时路由间仅有12条通路. 将不存在直接通路的路径长度设为无穷大， 将路由到其本身的路径长度设为0.

3) X网格(Mesh)图. 在实际情况中也存在这样一种情况， 路由与其相邻的八个路由存在通路. 在X网格模型中， 则共有2(N-1) ×(2N-1)条路径. 当N=3时， 此时路由间的通路为20条. 本研究将对这三种路由网络模型进行具体实验.

2.3 不相交多路径路由算法

1) 假设输入网络模型的大小为x×y、 需要发送数据包的路由对的数量m、 每对点需要发送的数据包数量P、 采用的路由网络模型为M、 路由i到路由j之间的最短路径为P[i][j], 其中i,j∈[1,x×y].

2) 通过输入数据自动生成路由网络模型， 每一条通路的路径长度均随机产生， 为了数据的可操作性， 本研究的随机范围在[1, 16].

3) 通过输入数据m， 自动生成m对起点和终点， 起点和终点对应的路由编号为[1,x×y]， 起点和终点不会是同一个点.

4) 每一对路由采用下式计算出路由对之间的最短路径：

(1)

其中:f[k][i][j]表示只经过前k个路由(包括k)， 从路由i到路由j的最短路径. 当k从1到x×y时， 即为经过所有中间路由， 从第i个路由到第j个路由的最短路径P[i][j].

利用下式对最短路径P[i][j]取反：

在实验中， 路由之间本为全通路， 为实现公式(2)效果， 就是将最短路径上路由改为单向通路， 即为将P[i][j]路径上的路径长度设为不可达， 从而得到新的网络模型M′. 此时， 重新调用公式(1)得到第i个路由到第j个路由的最短路径P′[i][j].

(3)

其中:S[i][j]表示最短路径P[i][j]和P′[i][j]之间共有的部分. 因此， 得到了两条多路径最短路径W1[i][j]和W2[i][j]， 如公式(4)所示：

其中:W1[i][j]和W2[i][j]分别表示经P[i][j]和P′[i][j]消除掉公共路径S[i][j]后， 所得到的多路径最短路径.

此外， 如果利用次优短路径或者另一条单路径最短路径(有时存在多条单路径最短路径)， 再按上述步骤4)， 在消除公共路径之后， 又可多获得两条多路径最短路径.

5) 分别从每对点的起点开始发包， 通过单路径发送定量的数据包. 以每对点需要发送的数据包数量为初始阈值， 统计经过每一条边的数据包总量， 并统计数据包总量超过阈值的边的数量， 最后令阈值以其初始值为基数成倍递增， 得出多组数据.

6) 分别从每对点的起点开始发包， 通过多路径发送给定量一半的数据包， 之后对每一条边都统计经过的数据包总量； 再以每对点需要发送的数据包数量为初始阈值， 统计流经数据包总量超过阈值的边的数量； 最后令阈值以其初始值为基数成倍递增， 得出多组数据.

7) 通过实验所得数据分别计算出单路径路由和多路径路由在边上的拥塞情况的协方差， 用协方差观察负载均衡.

8) 通过改变网络模型、 数据量等方法多次实验， 最后通过实验结果的总体情况得出一般性结论.

3 实验结果与分析

假设给定节点总数为n=x×y、 需要发送数据包的点对数量m， 节点间路径长度为[1， 16]中的随机整数， 需要发送数据包的起始节点和终止节点均随机产生.

3.1 单路径路由和多路径路由在完全图上的数据对比

完全图网络模型中的实验结果如图3所示， 通过9组对比实验， 本研究得到如下结论：

1) 通过对比图3(a)～(c)或3(d)～(f)或3(g)～(i)可知， 当点对数m不变的情况下， 节点数n越多， 多路径路由优于单路径路由的负载均衡效果越明显. 因此， 当给定点对m不变时， 节点个数n的取值越大， 多路径路由在负载均衡方面的优越性越明显.

2) 通过对比图3(a)、 3(d)、 3(g)或3(b)、 3(e)、 3(h)或3(c)、 3(f)、 3(i)可见， 当节点个数n取值不变时， 如果指定需要传输数据的点对数量m越多， 多路径路由和单路径路由的负载均衡结果趋于一致， 有时甚至还会出现单路径路由的负载均衡优于多路径的. 因此， 当给定节点个数n不变时， 改变给定点对数量m对实验结果影响不大.

3) 结合图3中的9组实验结果， 通过对比各组实验中单路径和多路径负载协方差的大小可知： 在所有情况下， 单路径负载协方差均大于多路径负载协方差.

4) 在实验参数不变的情况下(同一张图中)， 当给定阈值较小时， 单路径的过载边数与多路径过载边数区别较小， 有时还会略少于双路径； 而当阈值较大时， 多路径过载边数要明显少于单路径.

图3 完全图网络模型中的多路径与单路径负载均衡对比Fig.3 Multipath vs single path with respect to load balance in acomplete graph

3.2 单路径路由和多路径路由在Mesh图上的数据对比

Mesh网络模型中的实验结果如图4所示， 通过9组对比实验， 可得出如下结论：

1) 通过对比图4(a)～(c)或4(d)～(f)或4(g)～(i)， 当点对数m不变的情况下， 图中节点数n取值越大， 多路径路由相比于单路径路由的负载均衡优势越明显. 因此， 在点对m不变的情况下， 节点个数n越多， 在负载均衡方面， 多路径路由的优势越突出.

2) 通过对比图4(a)、 4(d)、 4(g)或4(b)、 4(e)、 4(h)或4(c)、 4(f)、 4(i)， 当给定的节点个数n不变的情况下， 指定需要传输数据的点对数量m越多， 多路径路由负载均衡的优越性越不明显， 有时甚至还会出现单路径路由负载均衡优于多路径的情况. 因此， 在给定的节点个数n不变的情况下， 点对数量m取值的变化， 并不会影响多路径路由和单路径路由在负载均衡方面的区别.

3) 通过对比各组实验中单路径和多路径负载协方差的大小可知： 在所有情况下， 单路径负载协方差都大于多路径负载协方差.

4) 在实验参数不变的情况下(同一张图中)， 如果阈值相对较小， 那么单路径的过载边数与多路径过载边数差别不大， 并且有时还会略少于双路径； 而在阈值相对较大的情况下， 多路径的过载边数要明显少于单路径.

图4 网格网络模型中的多路径与单路径负载均衡对比Fig.4 Multipath vs single path with respect to load balance in a Mesh

3.3 单路径和多路径路由在X-Mesh图上的数据对比

在X-Mesh网络模型中的实验结果如图5所示, 从图中的9组对比实验可知：

1) 通过对比图5(a)～(c)或5(d)～(f)或5(g)～(i)可知， 在点对数m不变的情况下， 节点数n越多， 多路径路由负载均衡相较于单路径路由负载均衡的优势越明显.

2) 通过对比图5(a)、 5(d)、 5(g)或5(b)、 5(e)、 5(h)或5(c)、 5(f)、 5(i)可见： 当节点个数n不变时， 如果需要传输数据的点对数量m越多， 那么多路径路由优于单路径路由负载均衡的优势越弱， 有时甚至还会出现单路径路由负载均衡优于多路径路由的情况.

3) 通过比较各组实验中单路径和多路径的负载协方差大小可知： 在所有情况下， 单路径负载协方差都大于多路径负载协方差.

图5 X-网格模型中的多路径与单路径负载均衡对比Fig.5 Multipath vs single path with respect to load balance in a X-Mesh

4) 在实验参数相同的情况下(同一张图中)， 当阈值相对较小时， 单路径的过载边数与多路径的差别不大， 有时还会略少于双路径； 而当阈值相对较大时， 多路径过载边数要明显少于单路径.

4 结论

本研究探讨了不相交多路径路由方案在软件定义网络中的可行性， 并实现了多路径路由算法. 通过模拟单路径路由和不相交多路径路由在网络数据传递中网络负载均衡上的差别， 验证了多路径路由在网络负载均衡上的优势. 此外， 实验结果还表明： 存在一个网络链路负载极限阈值(较小的值)， 当给定网络的负载阈值小于这个值时， 单路径路由有更优的负载均衡. 而大于这个值时多路径路由更优. 当网络链路负载极限阈值越大时， 不相交多路径路由对比单路径路由的优势越明显. 这表明， 多路径路由方案在高带宽的高速网络中具有更大的优势.

[1] LIPSEY R G, KELVIN L. The general theory of second best[J]. The Review of Economic Studies, 1956, 24(1): 11-32.

[2] AHUJA R K, MAGNANTI T L, ORLIN J B. Network flows: theory, algorithms, and applications[M]. New Jersey: Prentice Hall, 1993.

[3] KHULLER S, BARUCH S. Efficient parallel algorithms for testingkand finding disjoints-tpaths in graphs[J]. SIAM Journal on Computing, 1991, 20(2): 352-375.

[4] ORDA A, SPRINTSON A. Efficient algorithms for computing disjoint QoS paths[C]// Joint Conference of the IEEE Computer and Communications Societies. Hong Kong: IEEE, 2004: 727-738.

[5] GUO L K, SHEN H, LIAO K W. Improved approximation algorithms for computingkdisjoint paths subject to two constraints[J]. Journal of Combinatorial Optimization, 2015, 29(1): 153-164.

[6] GUO L K, LIAO K W, SHEN H,etal. Efficient approximation algorithms for computingkdisjoint restricted shortest paths[C]//ACM Symposium on Parallelism in Algorithms and Architectures. Portland: ACM, 2015: 62-64.

[7] 张朝昆, 崔勇, 唐翯祎, 等. 软件定义网络(SDN)研究进展[J]. 软件学报, 2015, 26(1): 62-81.

[8] JAIN R. Internet 3.0: ten problems with current internet architecture and solutions for the next generation[C]// IEEE Conference on Military Communications. Washington: IEEE, 2006: 1-9.

[9] NUNES B A A, MENDONCA M, NGUYEN X N,etal. A survey of software-defined networking: past, present, and future of programmable networks[J]. IEEE Communications Surveys and Tutorials, 2014, 16(3): 1 617-1 634.

[10] TENNENHOUSE D L, WETHERALL D J. Towards an active network architecture[C]//The IEEE DARPA Active Networks Conference and Exposition. San Francisco: IEEE, 2002: 2-15.

[11] GREENBERG A, HJALMTYSSON G, MALTZ D A,etal. A clean slate 4D approach to network control and management[J]. ACM Sigcomm Computer Communication Review, 2005, 35(5): 41-54.

[12] GUDE N, KOPONEN T, PETTIT J,etal. NOX: towards an operating system for networks[J]. ACM Sigcomm Computer Communication Review, 2008, 38(3): 105-110.

[13] 左青云, 陈鸣, 赵广松,等. 基于OpenFlow的SDN技术研究[J]. 软件学报, 2013, 24(5): 1 078-1 097.

[14] MCKEOWN N, ANDERSON T, BALAKRISHNAN H,etal. Openflow: enabling innovation in campus networks[J]. ACM Sigcomm Computer Communication Review, 2008, 38(2): 69-74.

[15] HOUGARDY S. The Floyd-Warshall algorithm on graphs with negative cycles[J]. Information Processing Letters, 2010, 110 (8/9): 279-281.

Performanceofmultipathroutingalgorithmsbasedonsoftwaredefinednetworkingparadigm

FU Mingjian1, 2， WU Fan2， HUANG Fangfang3， GUO Longkun2

(1. National Experimental Teaching Demonstration Center of Network Information Security and Computer Technology，Fuzhou University, Fuzhou, Fujian 350116, China;2. College of Mathematics and Computer Science， Fuzhou University， Fuzhou， Fujian 350116, China;3. State Grid Fujian Information and Telecommunication Company, Fuzhou, Fujian 350003, China)

Although disjoint multi-path routing has significant advantages in load balancing and fault tolerance, it is difficult to deploy in large-scale networks because of its high time complexity. To tackle this problem, the paper first analyzes the characteristics of software definition networking(SDN) paradigm, and consequently demonstrates the feasibility of the multiple disjoint routing scheme in SDN networks. Then, an algorithm for calculating disjoint paths is implemented based on network flow theory and graph properties of disjoint paths. Last but not the least, by designing a series of experiments in various network models, it is shown that routing based on multiple disjoint paths outperforms traditional routing based on single shortest path in load balancing. Meanwhile, the experimental results indicate that the performance of the algorithm is related to the load limit threshold of the links in networks.

software defined networking; multipath disjoint routing; load balance

10.7631/issn.1000-2243.2017.05.0628

1000-2243(2017)05-0628-07

TP393.01

A

2016-01-07

郭龙坤(1983-)， 副教授， 主要从事算法设计与分析、 软件定义网络等方面研究， lkguo@fzu.edu.cn

国家自然科学基金资助项目(61300025); 教育部博士点基金资助项目(20123514120013); 福建省自然科学基金资助项目(2017J01753)

(责任编辑： 林晓)