一种PSO-SVM的光伏阵列故障检测与分类

林培杰， 陈志聪， 吴丽君， 程树英

(福州大学物理与信息工程学院， 微纳器件与电池研究所， 福建 福州 350116)

一种PSO-SVM的光伏阵列故障检测与分类

林培杰， 陈志聪， 吴丽君， 程树英

(福州大学物理与信息工程学院， 微纳器件与电池研究所， 福建 福州 350116)

提出一种粒子群优化支持向量机的光伏阵列故障检测与分类的方法. 分析了光伏阵列输出特性和故障类型， 选择合适的特征向量及归一化方式. 选用径向基核函数优化模型结构， 并利用PSO算法对参数进行寻优， 提高模型精确度. 结合实验平台获取光伏阵列正常工作和8种故障状态的实测数据， 随机划分为训练集和测试集， 并建立PSO-SVM故障检测与分类模型. 实验表明， 应用本模型进行故障检测准确率达99.89%， 分类准确率达98.68%， 优于BP神经网络以及决策树的检测和分类结果.

光伏阵列； 故障; 检测; 分类； 粒子群优化； 支持向量机

0 引言

近年来， 随着光伏并网发电系统装机数量和容量不断增加， 为提高光伏电站的运行稳定性及其发电量， 人们对光伏电站的高效运行维护日益重视. 在光伏电站中， 光伏阵列作为其中最主要的一部分， 其工作状态会影响整个电站运行的效率及稳定性. 由于光伏阵列通常安装和工作在复杂的户外环境中， 受到热循环、 湿度、 紫外线、 阴影等各种环境因素的影响， 容易出现局部材料老化、 裂纹、 热斑、 开路或者短路等各种故障， 影响光伏组件使用寿命[1]. 同时， 故障的产生会降低电站的发电效率， 严重时甚至发生火灾， 导致财产损失[2]. 因此， 对光伏阵列在运行状态中出现的故障能够及时检测、 分类、 警报与排除， 就能减少光伏电站因不正常运行而导致的发电量损失， 防止故障扩散， 避免安全事故的发生， 从而提高光伏系统全生命周期内的安全性及总发电量.

学者们提出了一些用于光伏阵列故障检测与分类的不同方案. 文[3-4]提出一种新的光伏组件连接结构法， 采用CTCT结构， 在保持输出功率不变的情况下， 监测光伏系统工作状态, 再配合一定数量的传感器， 可以确定发生热斑故障的光伏组件位置. 基于该结构的故障诊断方案系统安装过程较复杂， 对于大型的光伏电站而言， 所需要的传感器数量巨大. 文[5-6]提出红外热成像法， 根据光伏组件在不同工作状态下呈现出的温度变化来判断是否存在例如热斑、 老化等故障， 对较大规模光伏阵列进行检测时需要高分辨率的热像仪. 文[7-8]提出对地电容测量法和时域反射分析法， 这两种方法都需要系统停止工作的情况下对光伏系统进行检测， 实时性较差. 随着机器学习算法在故障诊断中应用的发展， 越来越多的学者将其引入到光伏阵列故障诊断中， 例如决策树[9]、 神经网络[2, 10-12]等， 其中神经网络算法较为广泛. 文[9]通过将光伏面板的电压、 电流和工作温度、 照度作为输入训练决策树模型， 实现对光伏阵列故障检测和诊断. 文[2， 10]提出了采用BP神经网络的光伏组件故障诊断方法， 以光伏组件的开路电压、 短路电流、 最大功率点电压和电流作为输入到训练过的神经网络， 用以识别组件正常、 短路或者异常老化三种状态. 文[11]提出以光照强度、 组件工作温度、 最大功率点电压和电流作为输入， 组件的输出电压作为输出， 训练多个3层前馈神经网络模型， 实现单组串中光伏模块短路故障的识别和定位. 文[12]提出采用贝叶斯神经网络模型实现光伏组件的污染程度评估的方法， 模型以光照强度和太阳能电池温度作为输入， 光伏面板产生的功率作为输出.

支持向量机(SVM)采用结构风险最小化原则， 具有很强的泛化能力， 并克服了神经网络中存在的过拟合、 收敛速度慢、 容易陷入局部极值等缺点[13-14]， 在故障诊断等领域中有着广泛的应用[15-16]. 因此， 本研究拟将SVM应用于光伏阵列故障检测与分类中. 在实际应用中， SVM的精确度很大程度取决于参数的选取， 为高效获得SVM最优参数， 采用粒子群优化算法(PSO)对其进行寻优[17-18]. 因此， 本研究建立PSO-SVM光伏阵列故障诊断与分类模型， 仅以光伏阵列最大功率点处的电压和电流作为输入特征向量， 无需采集光伏阵列的工作温度和照度. 搭建实验平台， 模拟各种故障， 获取样本数据， 对模型进行训练并验证.

1 光伏阵列故障分析及特征提取

图1 光伏并网发电系统拓扑及故障示意图 Fig.1 Topological graph and typical faults of grid-connected PV system

典型的光伏并网发电系统如图1所示， 系统通常由光伏组件、 带有保护装置的汇流箱和具有最大功率跟踪(MPPT)功能的并网逆变器组成， 其中光伏组件通常采取SP的串并联形式进行连接.

在光伏并网运行中， 常见的故障有接地、 短路和失配故障[19-20]. 接地故障主要由于电缆的绝缘层损坏， 而导致光伏阵列中某些组件的连接线与支架相连； 短路故障主要由光伏组件老化、 振动、 电弧毁坏了绝缘线路造成绝缘失效、 安装不规范导致电池之间的短路等等. 短路故障将加大电弧产生的概率， 使组件输出的功率都消耗在故障点， 导致故障部分过热而损坏， 甚至引起火灾等严重后果； 失配故障发生在部分组件与其他组件在电气参数上产生较大的不一致， 失配故障包括有阴影、 组件/串的开路、 组件老化等缺陷. 根据故障类型， 主要针对光伏阵列的正常工作状态及比较常见的开路、 短路和阴影等故障进行研究， 如图1中所示的3种故障示意图， 实现对光伏阵列不同状态的识别和分类.

在STC下， 光伏阵列在正常状态和不同故障状态时的I-V和P-V特性曲线如图2所示. 从图2(a)中可以看出， 对比正常工作状态下， 发生故障的光伏阵列的I-V曲线会呈现不同的变化. 例如， 在局部组件开路状态下， 阵列的输出电流减少， 短路电流下降， 但开路电压不变； 在局部阴影情况下， 光伏阵列的I-V曲线将呈现阶梯变化等. 同时， 在不同的照度和温度下，I-V曲线将出现移动现象， 如果仅采用此曲线来对故障进行判断将较为困难. 由于并网逆变器的MPPT功能， 即使光伏阵列产生了故障， 只要其输出电压达到逆变器的工作电压， 逆变器可以让系统重新工作于最大功率点， 如图2(b)中所示. 当光伏阵列工作于正常状态时， 系统输出的功率将保持在A点， 此时若系统发生局部短路故障时， 系统功率点将转移至B点. 因此， 可以采用系统工作于最大功率点的电气参数Vmpp和Impp做为故障检测算法的输入特征参数. 本研究采用Matlab的Simulink平台， 搭建一组6×3光伏阵列并网发电系统仿真模型， 改变输入照度和温度， 模拟4种工作状态， 获取若干组Vmpp和Impp数据， 得到数据分布如图3所示.

图2 不同工作状态光伏特性曲线图Fig.2 PV characteristic curves under various conditions

图3 光伏阵列各种状态的电压-电流分布图Fig.3 Vmpp vs Impp of PV under various conditions

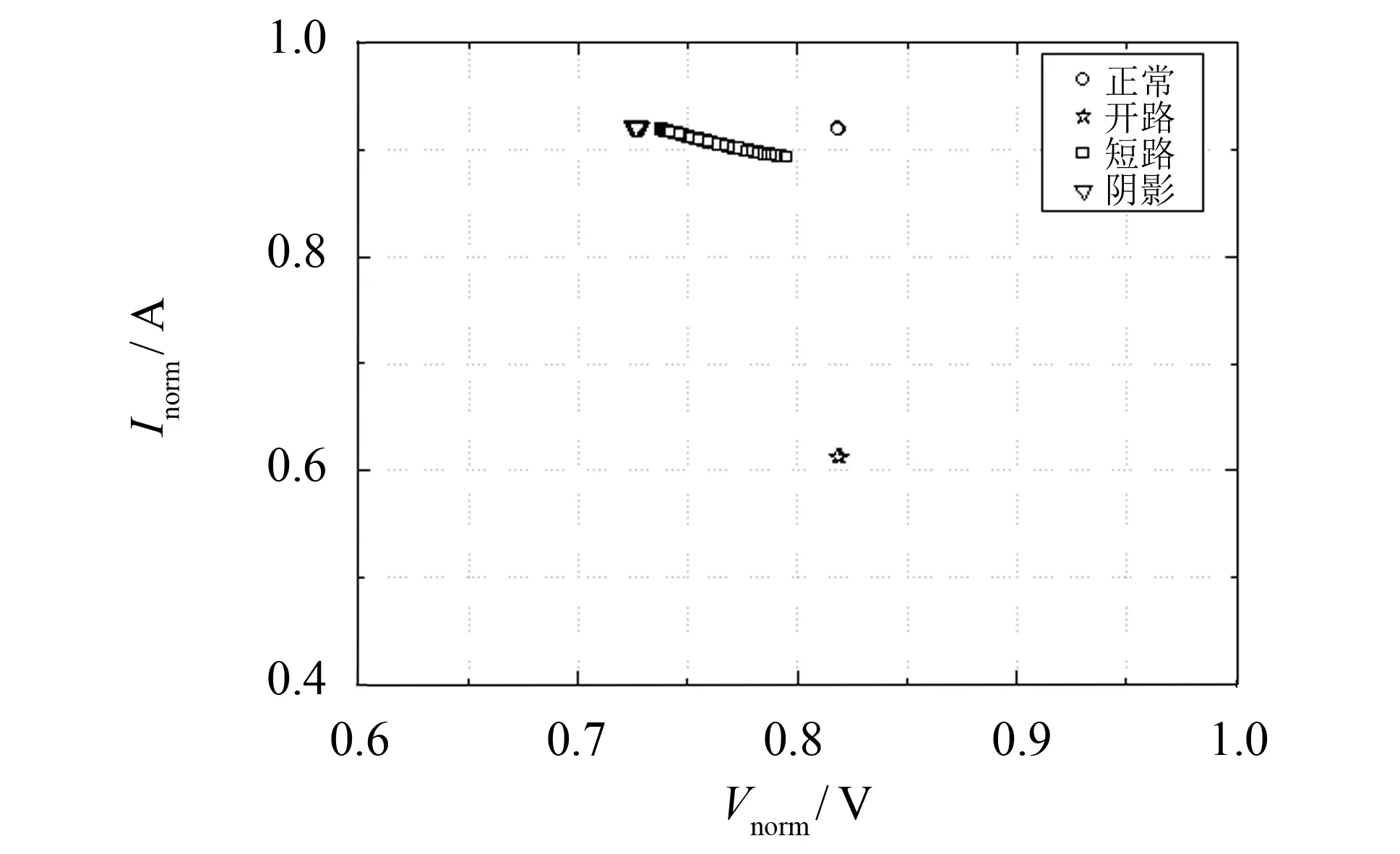
图4 光伏阵列仿真数据的Vnorm-Inorm分布图Fig.4 Simulated Vnorm vs Inormof PV under various conditions

从图3中可以看出， 4种光伏工作状态下光伏阵列的Vmpp和Impp数据分布有较多的交叠的地方， 这样不便于算法的识别和分类， 因此对其进行归一化[21]. 在光伏发电系统中， 选取两片与工作光伏阵列中组件参数一致的组件作为参考组件， 如图1中虚线框所示. 在实际应用中， 将这两块参考组件放置靠近工作光伏阵列， 使它们具有相同的工作环境. 在测量光伏阵列Vmpp和Impp的时候， 同步测量参考组件的开路电压Uoc-ref和短路电流Isc-ref， 并进行光伏阵列电压和电流的归一化， 具体计算公式如下：

式中：Vnorm为归一化后的电压参数；Inorm为归一化后的电流参数；Uoc-ref为参考光伏组件的开路电压；Isc-ref为参考光伏组件的短路电流；S为光伏阵列中单个组串的光伏组件数目；P为光伏阵列中并联的光伏组串的数目. 根据归一化后的数据， 得到光伏阵列各种状态的数据分布图如图4所示. 从图中可以看出， 数据的聚类效果较好. 因此， 以Vnorm和Inorm作为PSO-SVM的输入特征参数， 利于算法的识别和分类.

2 PSO-SVM故障诊断与分类模型

采用SVM算法实现光伏阵列的故障诊断和分类， 在SVM的使用过程中， 选择合适的核函数是一个重要的步骤， 其常用的核函数主要有多项式函数、 径向基函数(RBF)、 sigmoid函数[14]. 在几个核函数中， 根据实验测试， 采用RBF在一般情况下会获得更好的结果， 因此， 采用RBF作为核函数来建立SVM分类器. 同时， 核函数中的两个参数： 惩罚因子c和核参数γ将影响分类器的精度， 通过PSO寻优算法对c和γ的最优解进行寻找.

PSO算法是根据鸟类捕食行为启发而提出的一种群智能优化算法[22]. 在采用PSO算法针对问题进行优化时， 算法首先在可行解空间初始一群粒子， 每个粒子都成为优化问题的一个可行解， 具有位置和速度两个属性， 同时由目标函数确定其对应的适应度值， 由该值的大小来显示粒子的优劣. 每个粒子将在可行解空间中运动， 并根据粒子自身的飞行经验(个体极值)Pbest和群体的飞行经验(全体极值)Gbest来调整自身的位置和速度， 调整飞行轨迹向最优解靠拢. 假设一个D维的搜索空间中， 有N个粒子组成的种群X=(X1,X2, …,XN)， 对于第i个粒子，它的速度表示为Vi=(vi1,vi2, …,vid)， 位置表示为Xi=(xi1,xi2, …,xid)，粒子更新自己的速度和位置的公式如下：

图5 基于PSO的SVM参数寻优流程图Fig.5 Flow chart of optimizing the SVM parameters with PSO

式中：t与t+1代表算法的迭代属性；i∈[1,N]，N为粒子数；d∈[1,D]，D为粒子维度；vid表示粒子的速度；pid表示第i个粒子个体当前的最优解；pgd表示整个群体当前的最优解；xid表示粒子的位置；ω为惯性权重因子；c1和c2为加速因子；r1和r2为均匀分布于[0, 1]之间的随机数. 根据PSO算法的工作原理， 采用PSO对SVM参数寻优的算法流程可描述如图5所示.

算法的具体步骤如下：

① PSO参数初始化： 设置最大迭代步数MaxGen或给定目标函数评价值的最小精度Fmin， 设置种群数量N. 随机生成种群位置X=(X1,X2, …,Xi, …,XN)，Xi=(xic，xiγ)表示第i个粒子由两个分量构成， 分别代表SVM惩罚因子c和RBF参数γ的位置， 随机生成对应每一个位置的速度Vi=(vic,viγ). 设置位置和速度两个分量的限定范围， 分别为[Xcmin,Xcmax]和[Xγmin,Xγmax].

② 进行粒子适应度评估.

③ 根据适应度值更新个体极值及群体极值.

④ 按照粒子速度与位置更新公式进行更新. 每一轮更新结束后需要对超出位置的各分量值进行限定.

⑤ 判断是否满足结束条件， 若满足则结束寻优过程， 此时群体极值pgd即为所要求的最佳参数， 若不满足转至③继续进行寻优. 结束条件为寻优达到最大进化代数或目标函数评价值小于给定精度.

⑥ 寻优结束， 获得SVM最优参数， 根据最优参数训练SVM模型.

3 实验结果对比与分析

3.1 样本参数获取

根据图1所示的拓扑图， 搭建了一套1.8 kW的光伏并网发电和数据采集处理实验平台， 如图6所示.

图6 实验平台Fig.6 The experimental platform

表1 光伏组件和逆变器参数Tab.1 Parameters of PV module and inverter

系统采用了20块型号为GL-M100太阳能组件， 其中18块组件用于光伏并网， 分成3个组串， 每个组串采用6块组件串联， 组成6×3的连接方式， 另外2块用于Uoc-ref和Isc-ref的获取； 逆变器采用的型号为GW2000-NS， 光伏组件在STC下的输出数据和逆变器的具体参数如表1所示. 同时设计以ARM7为核心的数据采集模块， 采集光伏发电系统的电气参数Impp和总电压Vmpp以及参考电气参数Uoc-ref和Isc-ref， 并将数据传输至上位机处理平台.

针对搭建好的光伏阵列， 在其并网发电过程中进行各种故障模拟， 然后通过数据采集模块采集故障数据. 为更好体现算法对光伏阵列故障的诊断和分类， 在保证处于故障中的光伏阵列输出电压满足逆变器最低工作电压的基础上， 将前文所述的3种故障状态进行细化， 总共得到8种故障状态. 选取多个工作日对系统的各种工作状态进行模拟和数据随机采集. 采集的样本总数为23 857个， 每种工作状态的标签、 简称、 采集的样本数量及其所占总样本数的比例如表2所示. 其中， 局部阴影故障只模拟阴影发生在并网发电的光伏阵列上， 而不在参考组件上.

表2 用于PSO-SVM模型的数据样本Tab.2 Data set for the PSO-SVM model

图7 光伏阵列实测数据的Vnorm-Inorm分布图 Fig.7 Experimental Vnorm vs Inorm of PV under various conditions

通过归一化运算， 得到实测数据的Vnorm和Inorm的分布图如图7所示. 由于实验所采用的每个组件参数不是严格一致， 以及在数据采集过程中存在一定的噪声影响以及最大功率跟踪误差等原因， 可以看出实测数据分布不能达到图4中所示仿真数据的分布效果， 但仍然有一定的聚类效果， 其中开路1、 阴影3和阴影5这3种工作状态下存在非线性数据边界， 可以发现三者之间无法进行线性分割， 因此在本算法中采用RBF核函数， 将数据映射至高维空间再进行划分.

图8 基于PSO的SVM参数寻优结果Fig.8 Result of optimizing the SVM parameters with PSO

3.2 数据分析

不失一般性， 对3.1节所获样本数据随机分成3份， 选取其中2份作为训练集， 剩余1份作为测试集. 其中, 训练集样本用来对SVM分类模型训练， 测试集样本对训练后的模型进行验证. 在训练SVM分类模型时， 由于采用了RBF核函数， 其中参数c和γ将对SVM分类模型的准确性产生较大的影响. 因此， 采用PSO算法对c和γ的最佳参数进行优化. 采用训练集样本作为PSO优化过程的数据样本， 采用3折交叉验证的方式进行验证， 最后获得的最高分类准确率对应的c和γ的值就是最佳参数， 具体流程如图5所示. 设置PSO算法相关参数为惯性因子c1=1.5和c2=1.7， 种群大小为20， 进化代数为200, 得到的参数寻优结果如图8所示. SVM最优参数解为c=15.724 6，g=1 000， 其中g代表RBF核参数γ.

为比较所采用的PSO-SVM光伏阵列故障诊断和分类模型的性能， 分别采用文[2]、 文[10]所采用的BP神经网络(BPNN)算法和文[9]所采用的决策树(DT)算法对相同的样本集进行建模对比. BPNN采用单隐含层， 经过多次试验， 网络的输入层、 隐含层、 输出层的节点数选为2、 15、 9， 隐含层和输出层传递函数分别选用tansig和pureline函数， 训练方法选用L-M算法， 学习速率为0.01， 目标误差为0.000 1； DT 采用CART算法， 故障检测时采用节点数31个， 叶子节点数10个； 故障分类时采用节点数513个， 叶子节点数为142个. 在结果的对比上， 采用故障检测准确率和故障分类准确率两种数据来对比. 故障检测准确率代表的是分类器正确检测到光伏阵列处于 “正常工作”(即表2中标签为“1”的类别)和处于“故障状态”(即表2中标签为“2”至“9”的类别)的样本总数除以测试样本的总样本数； 故障分类准确率为光伏阵列工作状态每一类别的正确检测样本数之和除以测试样本的总样本数.

表3 光伏阵列不同工作状态分类准确率Tab.3 Classification accuracy of PV under various conditions (%)

经过各种算法的计算， PSO-SVM、 BPNN和DT的故障检测准确率分别为99.89%、 99.87%和99.87%， 故障分类准确率分别为98.68%、 95.74%和96.87%. 可以看出, 在故障检测上3种模型均有较高的准确率， 其中本方案具有最好的精度； 在故障分类上， 本算法达到98.68%， 分别比DT模型和BPNN模型高出1.81%和2.94%， 同样获得了最好的精度.

针对故障分类准确率进行细分， 计算光伏阵列每个工作状态的分类准确率， 即将每个类别检测的正确样本数除以各自的样本总数， 得到3种模型对光伏阵列不同工作状态的分类准确率对比数据， 如表3所示.

从表中可见， 在“正常”“开路2”“短路1”“短路2”“阴影2”“阴影22”这6种工作状态下， 3种模型的分类准确率都可达到98%以上； 在“开路2”“短路2”和“阴影22”这三种状态下， 3种分类模型均达到100%的准确率. 在开路1、 阴影3和阴影5这3种数据分布存在部分重叠的工作状态下， 只有PSO-SVM模型的准确率均可达到90%以上， 最高达到98.29%.

4 结语

光伏阵列在并网发电运行过程中， 由于自身或环境因素等原因可能引起不同的故障， 实现故障的精确检测及分类， 对提高光伏系统的发电效率和延长组件的工作寿命至关重要. 利用PSO-SVM建立了光伏阵列故障检测与分类模型， 为了使分类器达到更好的精确度， 通过PSO算法进行模型惩罚因子c和RBF核参数γ最优参数的寻找， 避免了人为随机选取参数而降低模型的精度. 以3×6光伏并网发电阵列作为实验平台， 在不同的气候条件下随机获得故障样本数据， 并对模型进行训练与测试， 表明模型对光伏阵列故障检测和分类效果较好. 同时， 分别与BPNN模型和DT模型的检测和分类准确率进行对比， 结果表明PSO-SVM模型具有更好的表现. 本方法适于光伏阵列故障诊断和分类.

[1] SHARMA V, CHANDEL S S. Performance and degradation analysis for long term reliability of solar photovoltaic systems: a review[J]. Renewable and Sustainable Energy Reviews, 2013, 27: 753-767.

[2] 王元章， 李智华， 吴春华， 等． 基于 BP 神经网络的光伏组件在线故障诊断[J]． 电网技术， 2013， 37(8)： 2 094-2 100．

[3] LIU Y L, LI B F, CHENG Z. Research on PV module structure based on fault detection[C]// Proceedings of 2010 Chinese Control and Decision Conference. Xuzhou: IEEE, 2010: 3 891-3 895.

[4] 程泽， 李兵峰， 刘力， 等． 一种新型结构的光伏阵列故障检测方法[J]． 电子测量与仪器学报， 2010， 24(2)： 131-136．

[5] 王培珍， 郑诗程． 基于红外图像的太阳能光伏阵列故障分析[J]． 太阳能学报， 2010， 31(2)： 197-202．

[6] BUERHOP C, Schlegel D, NIESS M,etal. Reliability of IR-imaging of PV-plants under operating conditions[J]. Solar Energy Materials and Solar Cells, 2012, 107: 154-164.

[7] TAKASHIMA T, YAMAGUCHI J, ISHIDA M. Fault detection by signal response in PV module strings[C]// Proceedings of 33rdIEEE Photovoltaic Specialists Conference. California: IEEE, 2008: 1-5.

[8] TAKASHIMA T, YAMAGUCHI J, OTANI K,etal. Experimental studies of fault location in PV module strings[J]. Solar Energy Materials and Solar Cells, 2009, 93(6): 1 079-1 082.

[9] ZHAO Y, YANG L, LEHMAN B,etal． Decision tree-based fault detection and classification in solar photovoltaic arrays[C]// Proceedings of 27thAnnual IEEE Applied Power Electronics Conference and Exposition. Florida: IEEE, 2012: 93-99.

[10] 王元章， 吴春华， 周笛青， 等． 基于 BP 神经网络的光伏阵列故障诊断研究[J]． 电力系统保护与控制， 2013， 41(16)： 108-114．

[11] SYAFARUDDIN S, KARATEPE E, HIYAMA T. Controlling of artificial neural network for fault diagnosis of photovoltaic array[C]// Proceedings of 16thInternational Conference on Intelligent System Application to Power Systems. Hersonissos: IEEE, 2011: 1-6.

[12] PAVAN A M, MELLIT A, DE PIERI D,etal. A comparison between BNN and regression polynomial methods for the evaluation of the effect of soiling in large scale photovoltaic plants[J]. Applied Energy, 2013, 108: 392-401.

[13] VAPNIK V N, VAPNIK V. Statistical learning theory[M]. New York: Wiley, 1998.

[14] CHANG C C， LIN C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 27.

[15] WIDODO A, YANG B S. Support vector machine in machine condition monitoring and fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2 560-2 574.

[16] 汤昶烽， 卫志农， 李志杰， 等． 基于因子分析和支持向量机的电网故障风险评估[J]． 电网技术， 2013， 37(4)： 1 039-1 044．

[17] 梅飞， 梅军， 郑建勇， 等． 粒子群优化的 KFCM 及 SVM 诊断模型在断路器故障诊断中的应用[J]． 中国电机工程学报， 2013， 33(36)： 134-141．

[18] 尹玉娟， 王媚， 张金江， 等． 一种自主核优化的二值粒子群优化: 多核学习支持向量机变压器故障诊断方法[J]． 电网技术， 2012， 36(7)： 249-254．

[19] FORMAN S E. Performance of experimental terrestrial photovoltaic modules[J]. IEEE Transactions on Reliability, 1982, 31(3): 235-245.

[20] MEYER E L, VAN DYK E E. Assessing the reliability and degradation of photovoltaic module performance parameters[J]. IEEE Transactions on Reliability, 2004, 53(1): 83-92.

[21] ZHAO Y, LEHMAN B, BALL R,etal． Graph-based semi-supervised learning for fault detection and classification in solar photovoltaic arrays[C]// Proceedings of IEEE Energy Conversion Congress and Exposition. Colorado: IEEE, 2013: 1 628-1 634.

[22] KENNEDY J. Particle swarm optimization[M]. New York: Springer, 2011: 760-766.

FaultdetectionandclassificationforphotovoltaicarraysbasedonPSO-SVM

LIN Peijie, CHEN Zhicong， WU Lijun， CHENG Shuying

(Institute of Micro-Nano Devices and Solar Cells， College of Physics and Information Engineering，Fuzhou University， Fuzhou， Fujian 350116， China))

A fault detection and classification model for photovoltaic arrays is presented by using particle swarm optimization-support vector machine(PSO-SVM). The characteristic and faults of PV arrays are analyzed. Moreover, the appropriate feature vectors are selected and the normalized method is designed, respectively. In order to strengthen the accuracy of the proposed model, the RBF kernel function is applied to improve the model structure, whose parameters are optimized by the PSO algorithm. Based on the measured platform, the experiment data set of the PV array under normal working condition and eight types of faults are recorded. The data set are randomly divided into testing set and training set to train the PSO-SVM model. The accuracy of fault detection and fault classification are 99.89% and 98.68%, respectively, which are superior to those of BP neural network and decision tree.

photovoltaic arrays; fault; detection; classification; particle swarm optimization; support vector machine

10.7631/issn.1000-2243.2017.05.0652

1000-2243(2017)05-0652-07

TM91

A

2016-03-10

程树英(1966-), 教授， 主要从事光伏材料、 器件及光伏发电系统等研究， sycheng@fzu.edu.cn

国家自然科学基金资助项目(61574038、 61601127、 51508105)； 福建省科技厅工业引导性重点资助项目(2015H0021、 2015J05124、 2016H6012)； 福建省教育厅科研资助项目(JAT160073)； 福建省经信委行业关键共性技术资助项目(83016006、 830020)

(责任编辑： 沈芸)