基于一类本原矩阵的非负矩阵Perron根的算法

王信存，吕洪斌，张 嫒

(1.辽东学院师范学院，辽宁 丹东 118003；2.北华大学数学与统计学院，吉林 吉林 132013)

基于一类本原矩阵的非负矩阵Perron根的算法

王信存1，吕洪斌2，张 嫒2

(1.辽东学院师范学院，辽宁 丹东 118003；2.北华大学数学与统计学院，吉林 吉林 132013)

利用矩阵的对角相似变换和Perron-Frobenius定理，给出了一类迹非零的不可约非负矩阵Perron根的简单数值算法，该算法仅需在迭代的每一步选择上次迭代矩阵的行和构成的正对角矩阵做矩阵的相似变换.同时通过适当的矩阵平移，此算法可适用于所有不可约非负矩阵Perron根的计算.

不可约非负矩阵；Perron根；数值算法

非负矩阵是非常重要的矩阵类，在数值分析、概率统计、组合分析、数理经济等领域具有重要应用.[1-2]对非负矩阵Perron根的估计与计算是非负矩阵理论中的经典内容.[3]在无线网络资源分配设计以及在研发相关策略时，非负矩阵Perron根的不同性质被证明对于理解不同优化对象的基本权衡关系至关重要.[4]关于非负矩阵Perron根的计算已有多种算法，如幂法[5]、基于幂法的本原矩阵最大特征值算法[6-7]、对角相似变换的迭代法[8-9]以及考虑参数选择的对角相似迭代算法[10]等.本文将给出一类迹非零的不可约非负矩阵Perron根的数值算法，进一步给出不可约非负矩阵类的Perron根的数值算法.

1 预备知识

关于非负矩阵Perron根的界，有著名的Perron-Frobenius定理：

定理1设A=(aij)∈Nn，ρ(A)是A之Perron根，则有

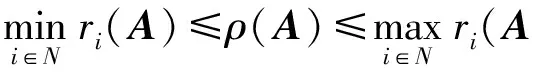
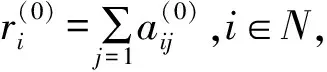
容易证明下述结果：

引理1设A∈Nn不可约.∀γ∈C(A)，记γ：i1→i2→…→ir→ir+1=i1，则∀m∈Z+，有

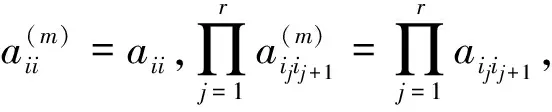
引理3设A∈Nn不可约.如果aij>0，i，j∈N，则

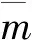
2 主要结果

定理2设A∈Nn不可约，且存在i0∈N，使得ai0i0>0，ρ(A)是A之Perron根.则

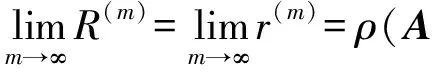
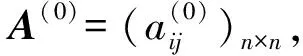
因为A不可约，所以其有向图Γ(A)是强连通的.[1]又对∀m∈Z+，A与A(m)有相同的零元模式，所以Γ(A(m))也是强连通的.对i0∈N，分以下几种情况讨论：

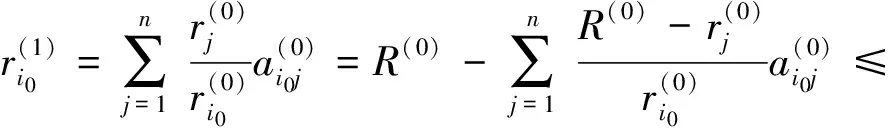
(1)

由(1)式，类似地有

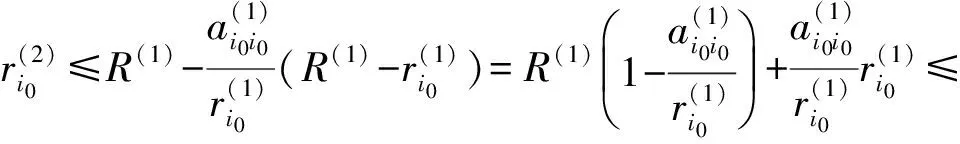
进一步有

⋮

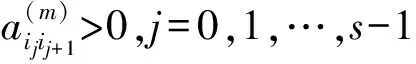
因此，∀i∈N，

进一步，∀k∈Z+有

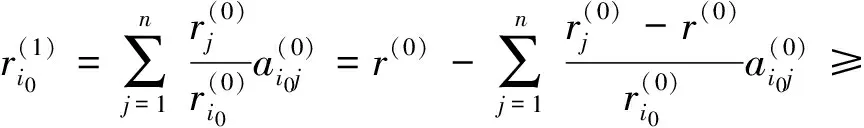
(2)

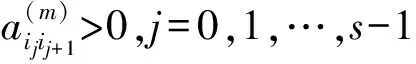
因此，对∀i∈N，

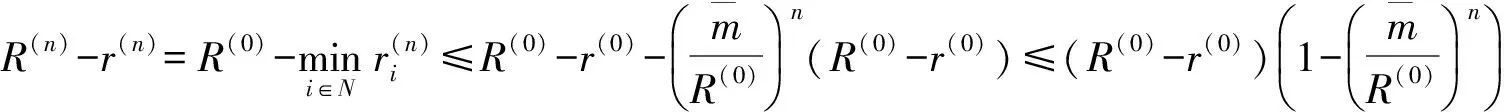
对∀k∈Z+，

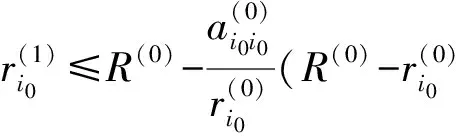
类似情形(ⅰ)的讨论有

同样，由A的不可约性，对∀i∈N，i≠i0，类似上面的讨论有

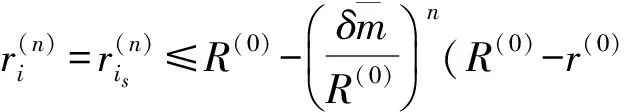
故∀i∈N，

进而∀k∈Z+，

综合情形(ⅰ)—(ⅲ)知定理为真.证毕.

注1对于不可约非负矩阵，若aii=0，∀i∈N，则可记B=A+cI，c>0(I为单位阵).应用定理1计算得ρ(B)=ρ(A)+c，因此定理1给出了所有不可约非负矩阵Perron根的算法.

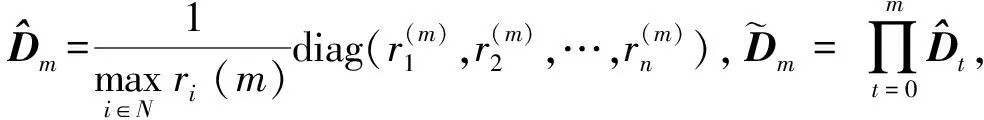
故有

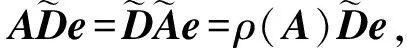
即

Ax=ρ(A)x.

3 算法与数值例子

本文算法：

步骤0 给出不可约非负矩阵A=(aij)n×n，ε>0，满足trA>0；

步骤2 如果rmax-rmin<ε，则转至步骤4，否则转至步骤3；

步骤3 令D=diag(r1，r2，…，rn)，D-1AD∶=A，转至步骤1；

步骤4 输出ρ(A)=(rmax+rmin)/2.

对于不可约非负矩阵A，如果trA=0，则可取c>0(如取c=(rmax-rmin)/n)做矩阵平移，用上述算法计算B∶=A+cI的Perron根，则有ρ(A)=ρ(B)-c.

下面应用MATLAB给出一个例子分析算法.

例1

应用本文算法和文献[7-8]的算法计算矩阵A的最大特征值的结果比较见表1.

表1 不同算法计算ρ(A)之迭代次数比较

由表1可知，本文算法与文献[7-8]算法比较具有更加简单、高效的特点.另外，根据定理1及本文算法，可以给出不可约非负矩阵之Perron向量的数值算法.

[1] BERMAN A，PLEMMONS R J.Nonnegative matrices in the mathematical sciences[M].New York：Society for Industrial and Applied Mathematics，1994：142-298.

[2] BAPAT R B，RAGHAVAN T E.Nonnegative matrices and applications[M].Cambridge：Cambridge University Press，1997：24-57.

[3] HORN R A，JOHNSON R C.Matrix analysis[M].New York：Cambridge University Press，2013：492-500.

[5] GOLUB G H，VAN LOAN G F.Matrix Computations[M].Baltimore：Johns University Press，1996：381.

[6] VARGA R S.Matrix iterative analysis[M].Berlin：Springer-Verlag，2000：52.

[7] DUAN F J，ZHANG K C.An algorithm of diagonal transformation for Perron root of nonnegative irreducible matrices[J].Applied Mathematics and Computation，2006，175：762-772.

[8] 王信存，吕洪斌.基于幂函数非负矩阵最大特征根的算法[J].吉林大学学报(理学版)，2017，55(3)：564-570.

[9] Bunse w.A Class of diagonal transformation methods for the computation of the spectral radius of a nonnegative irreducible matrix[J].SIAM J Numer Anal，1981，18(4)：694-704.

[10] 吕洪斌.不可约非负矩阵谱半径的数值算法[J].吉林大学学报(理学版)，2008，46(1)：6-12.

AnalgorithmforcalculatingPerronrootsofnonnegativematrixbasedonakindofprimitivematrix

WANG Xin-chun1，LYU Hong-bin2，ZHANG Yuan2

(1.Teachers College，Eastern Liaodong University，Dandong 118003，China；2.School of Mathematics and Statistics，Beihua University，Jilin 132013，China)

Using the diagonal similarity transformation and Perron-Frobenius theorem of matrix，a simple numerical algorithm for calculating Perron roots of a class of irreducible nonnegative matrix with nonzero trace is given.In this algorithm，it only needs to choose the positive diagonal matrix composed of the row sums of last iterative matrix in every step of the iteration and to do similarity transformation of matrix.At the same time，through proper matrix translation，this algorithm is applicable to the calculation of Perron roots of all irreducible nonnegative matrices.

irreducible nonnegative matrix；Perron root；algorithm

1000-1832(2017)04-0038-05

10.16163/j.cnki.22-1123/n.2017.04.008

2017-03-09

国家自然科学基金资助项目(51178001).

王信存(1973—)，男，硕士，副教授，主要从事矩阵理论及其应用、数值代数、图像处理研究；通信作者：吕洪斌(1964—)，男，博士，教授，主要从事矩阵理论及其应用、数值代数、数值计算研究.

O 241.6学科代码110·21

A

(责任编辑：李亚军)