基于非谐振节点的波导滤波器设计
赵 白
(河南水利与环境职业学院基础部,河南 郑州 450008)
基于非谐振节点的波导滤波器设计
赵 白
(河南水利与环境职业学院基础部,河南 郑州 450008)
阐述了基于非谐振节点的广义耦合系数的提取、外部品质因数的理论,并结合波导滤波器的制作方法,设计了一款包含非谐振节点(NRN)元件的脊型波导滤波器.在结构上对该滤波器进行了创新,利用非谐振节点的方式,在指定频率点处产生传输零点,使带外抑制提高了40 dB,回波损耗也达到指标要求.滤波器选为六阶带通波导滤波器,中心频率为5 GHz、带宽为200 MHz,HFSS中的仿真结果与理想结果较吻合,证明该设计是合理、可行的.
非谐振节点;耦合系数提取;外部品质因数;波导滤波器
0 引言
频率选择是滤波器所具有的特性,它的性能好坏会直接影响通信系统的整体性能.随着信息技术的发展,对滤波器的指标要求越来越高,因此滤波器对信号必须有更好的选择性或抑制性,从而使频谱资源得到较好的利用.传统的滤波器通过增加阶数的方式提高频率选择性,而这样会增加滤波器的插损和体积.引入传输零点的基于非谐振节点的滤波器在这方面则体现出其优越性.在工程设计中,系统整体结构或者部分器件的形状、尺寸都会受到严格限制,传统的微波滤波器通过在非相邻谐振器腔体间产生交叉耦合的方式来解决,但这样也会造成结构不稳定、难于调试等问题.[1]此外,当要求具有较高的频率值时,相应的滤波器尺寸必须设计得较小,由此也会造成工程上的装配困难、固定其仿真中使用同轴线等问题.针对此类问题,利用非谐振腔结构能够在有限频率点处产生最大数量的传输零点而不需要源和负载的直接耦合,达到器件尺寸与带外抑制效果的兼顾.[2-6]同时,由于传输零点的位置可以通过调节谐振器的谐振频率自由地控制,因此该类型的滤波器还具有模块化设计的优势.本文将非谐振节点理论应用于波导滤波器设计中,使设计的滤波器具有体积小、品质因数高、稳定性好等优点,具有一定的应用价值.
1 基本理论

图1 单腔双负载极点提取部分的等效电路
1.1 广义耦合系数的提取
图1给出了一个单腔双负载极点提取部分的等效电路,其中J0和JN表示导纳变换器,谐振器可以看做是电容与非频变电纳B1并联组成的一个整体.而另一个非频变电纳BN表示一个非谐振节点.此电路为带有单位负载G的双负载电路.利用该电路的对称性、奇偶模技术可以用来分析电路的原型.
反射系数S11表示为

(1)
其中
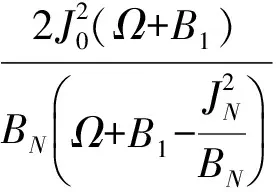
(2)
而Ω是可以从实频f中通过标准的带通到低通变换的方法得到其低通原型频率,公式为
(3)
其中f0为所设计滤波器的中心频率,而d(FBW)是相对带宽.
典型的双负载极点提取原型电路的频率响应如图2所示.原型电路在ΩZ处产生一个传输零点,而位于ΩP处产生一个反射零点,计算公式为:
ΩZ=-B1;
(4)

(5)
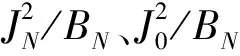

(6)
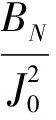
(7)
考虑到公式(4)与(5),B1和kN可以从实测或仿真数据中提取出来,即:
B1=-ΩZ;
(8)
(9)
从(6)—(9)式可知,若将传输零点置于滤波器通带的上方,那么非谐振节点的电纳值BN的符号为负,同样也可以将传输零点置于通频带的下方,则BN符号为正.同时,(9)式表明2个本征模之间的空间由广义耦合系数kN的绝对值确定.
1.2 外部品质因数
与文献[1]中的传统谐振器类似,通过对-3 dB带宽ΔΩ3dB估计可以提取出外部品质因数.从(1)式可得出当|F(Ω3dB)|=1时,S11的幅值为-3 dB.由此可推导出:

(10)
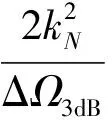
(11)
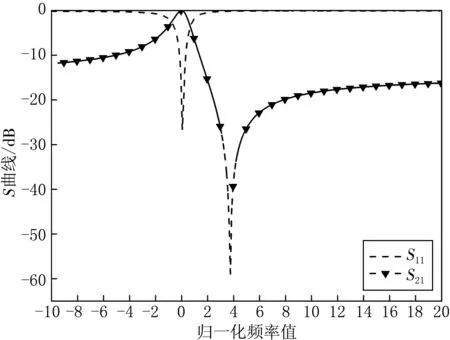
图2 双负载极点提取原型电路的频率响应曲线

图3 广义外部品质因数的提取
2 波导滤波器的设计实例
为证明广义耦合系数提取技术的实用性,设计一款带有2个传输零点的六阶带通波导滤波器(见图4).此滤波器需要满足以下电气特性:
(1) 中心频率为 5 GHz;
(2) 通带频率为 4.9~5.1 GHz;
(3) 回波损耗为 20 dB;
(4) 带外传输零点为 4.82,5.18 GHz.

图4 六阶低通原型滤波器拓扑图
2.1 综合技术
为了综合满足以上技术指标的滤波器原型,依据文献[2]中提出的应用于带有非谐振节点滤波器的综合技术,可得到耦合矩阵M的表达式:
(12)
根据本文中提到的广义耦合系数提取方法以及文献[6],得到:M11=0.440 6,M22= 1.238 5,M33=1.811 3,M44=0.182 8,M55= -0.179 4,M66=-1.192 3,M77=-1.853 1,M88= -0.428 6,M12=0.739,M23=1.3,M24=0.522 77,M45=0.581 6,M56=0.506 1,M67=1.3,M68= 0.714 5.
2.2 仿真实现
本文选用波导滤波器[7-8]实现以上技术指标,首先根据文献[7]中有关波导滤波器的制作方法并结合六阶低通原型滤波器拓扑图得出如图5所示的脊型波导结构技术指标.然后在HFSS软件中根据图5所示的指标得出整体的模拟仿真结构,如图6所示.根据文献[7]在HFSS中建立耦合矩阵元素与图5所示技术指标之间的关系,通过改变技术指标各个变量的值,逐渐地逼近耦合元素中的理想值,从而确定模拟仿真图6中各个变量的实际值.
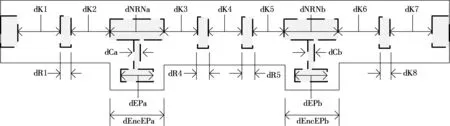
图5 脊型结构的波导滤波器的技术指标

图6 HFSS中脊型结构的波导滤波器仿真模型
各个技术指标在HFSS中设为变量,经过不断地迭代最终选择最接近理想耦合矩阵M的技术指标,此时仿真过程结束,可将所得的技术指标作为标准进行实物加工.迭代过后的各个技术指标的值见表1.
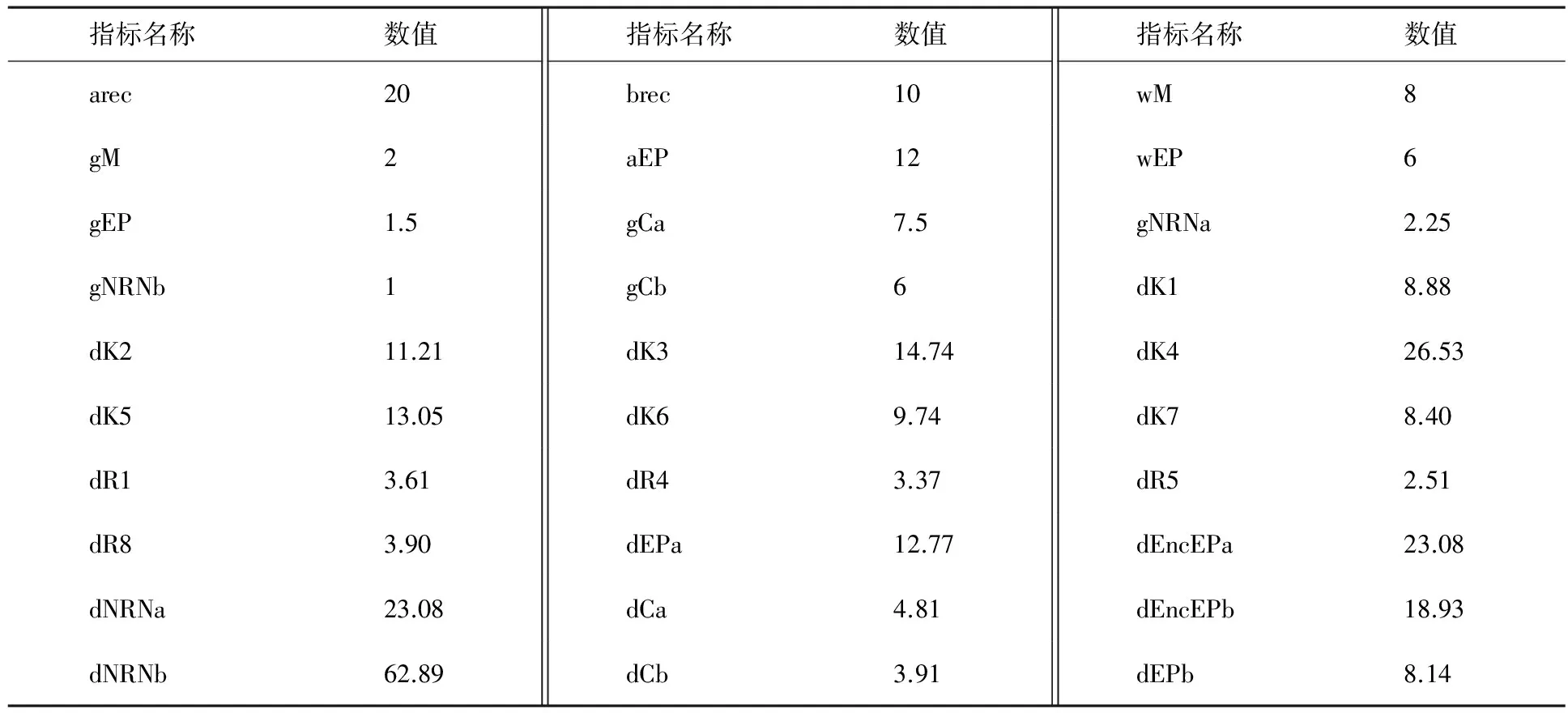
表1 HFSS中技术指标长度的最终值 mm
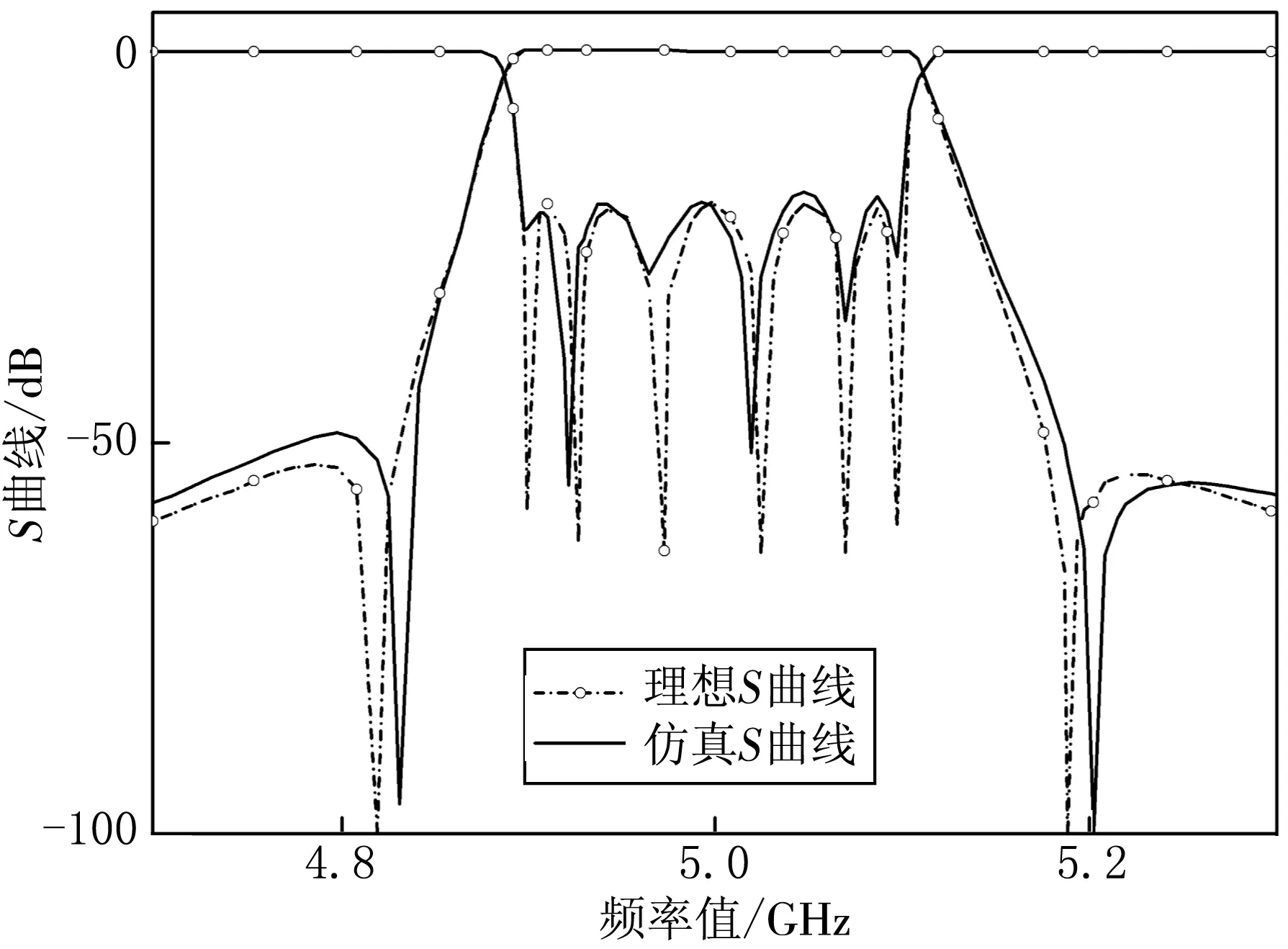
图7 理想曲线与仿真曲线结果对比
将表1中确定的尺寸参数在波导滤波器中进行仿真,可得图7所示的仿真曲线.由图7可以看出,由于阻带高低两端引入传输零点,使带外抑制提高了40 dB,并且回波损耗也达到20 dB的技术要求.由理论得到的理想频率响应曲线与HFSS仿真得到的结果基本吻合.
3 结论
本文研究了应用于谐振节点与非谐振节点之间的广义耦合系数的提取技术.并且使用这些理论设计了一款结构新颖并且无须交叉耦合就可在阻带高低两端引入传输零点的六阶广义切比雪夫带通滤波器.此滤波器结合了模块化设计和波导滤波器的优势,具有稳定、方便、易于调试以及低损耗、高品质因数的特点.经过HFSS仿真,理论值与仿真结果基本吻合,证明本文设计是正确的,具有一定的工程应用价值.
[1] ATIA A E,WILLIAMS A E.New type of waveguide bandpass filters for satellite transponders [J].Comsat Technical Reviews,1971,1(1):21-43.
[2] HEZ H,YOU C J,LENG S P,et al.Compact inline substrate integrated waveguide filter with enhanced selectivity using new non-resonating node[J].Electronics Letters,2016,52(13):1778-1780.
[3] XIAO Y,LI T,SUN H J.A novel W-band waveguide bandpass filter based on nonresonating nodes [C]//2016 9th International Conference on Microwave and Millimeter Wave Technology,ICMMT 2016-Proceedings,Beijing:IEEE,2016:833-835.
[4] MACCHIARELLA G.Generalized coupling coefficient for filters with nonresonant nodes [J].Microwave and Wireless Components Letters,2008,18(12):773-775.
[5] FAHMI M,RUIZ C J,MANSOUR R.Compact ridge waveguide filters using non-resonating nodes [J].IEEE MTT-S International Microwave Symposium Digest (IMS),2009,57(12):1337-1340.
[6] GLUBOKOV O,BUDIMIR D.Extraction of generalized coupling coefficients for inline extracted pole filters with nonresonating nodes [J].IEEE Transactions on Microwave Theory and Techniques,2011,59(12):3023-3029.
[7] 靳俊叶.新型波导滤波器研究及其应用[D].成都:电子科技大学,2014.
[8] 王胜.新型太赫兹波导滤波器的研究[D].成都:电子科技大学,2014.
Thedesignofwaveguidefilterbasedonnonresonatingnodes
ZHAO Bai
(Department of Basis,Henan Vocational College of Water Conservancy and Environment,Zhengzhou 450008,China)
The theories of extraction of generalized coupling coefficients including nonresonating nodes and external quality factor are introduced.On the basis,a ridge waveguide filter with nonresonating nodes is designed,employing the waveguide filter manufacturing method.This filter is a novel structure which successfully brings in the transmission zero in the certain frequency by nonresonating nodes.This kind of design makes the out of band suppression enhance remarkably,larger than 20 dB,and its return loss meet the qualification which has value in engineering.In this paper,it takes a 6-order waveguide bandpass filter as the example,whose center frequency is 5 GHz and bandwidth is 200 MHz.It is simulated in HFSS,and the simulation results obtained show very good agreement with desirable outcomes,which proves the design is reasonable and feasible.
nonresonating nodes;extraction of coupling coefficients;external quality factor;waveguide filter
1000-1832(2017)04-0054-05
10.16163/j.cnki.22-1123/n.2017.04.011
2016-12-30
国家自然科学基金资助项目(61131002).
赵白(1963—),男,高级讲师,主要从事滤波器设计研究.
TN 713学科代码510·50
A
(责任编辑:石绍庆)

