DCM模式逆变器的定环宽电压滞环控制

吴靖南，张宇，关清心

（华中科技大学电气与电子工程学院，武汉430074）

0 引 言

常见的逆变器有三种闭环控制方式：单闭环反馈控制、双闭环反馈控制和滞环控制，单闭环反馈控制又分为电压平均值反馈控制、电压瞬时值反馈控制和电流瞬时值反馈控制，滞环控制分为电压滞环控制和电流滞环控制。电压平均值反馈控制虽然结构和算法相对其它控制方式简单，但有着对输出波形不敏感的严重缺陷；电压瞬时值反馈控制和电流瞬时值反馈控制动态响应速度缓慢，负载适应性差［1］；双闭环反馈控制虽然具有良好的动态性能，可电流内环为抑制非线性负载扰动，必须具备足够高的带宽才能获得满意的性能，实现难度较大［2］；而基于双闭环控制发展的双环PID控制方式需要很大的内存空间存储历次偏差的信号值，同样较难实施［3］；相比之下，基于负载输出电压（电流）的电压（电流）滞环控制既能够实现单环控制策略中输出电压（电流）可控，具有快速的瞬态响应能力，又因是一个一阶无条件稳定系统，使得系统整体具有较高的稳定性，兼具单环控制和双环控制的优点。

随着逆变电源的广泛使用，使用者对于逆变电源的工作效率也有了越来越高的要求。传统的逆变器控制装置负载工作在连续导通模式（CCM），开关管的开关损耗会随着其导通频率的增加而增大，继而降低逆变器的效率［4］，因此目前降低线路损耗的普遍做法便是采用软开关技术。为实现开关管的软开关，可从硬件上进行改进或从软件上进行策略优化，硬件上，可通过附加谐振电路实现开关管的零电压开通（Zero Voltage Switching，ZVS）［5-6］，但硬件的解决思路虽然能避免在开关管上产生损耗，却同样会在谐振电路的元件上消耗电能，且谐振过程会给开关器件带来较高的电压电流应力，并不具有的实用价值，因此大多数研究基于控制策略进行改进从软件上实现软开关。文献［7］提出了一种全桥Boost电路基于不连续导通模式（DCM）的软开关运行策略，文献［8］基于临界导通模式（BCM）的零电压开通方式，文献［9］提出了基于混合导通模式的 Boost PFC电路优化及控制策略，文献［10-11］通过电流的反馈实现开关管零电流开通，为软开关控制技术提供了参考。软开关分析方法建模过程常采用状态空间平均法，该方法虽然能对控制对象有较好的描述，却要求逆变器的输出频率远小于开关器件的开关频率才能做低频等效，受限于开关管的开关频率，而采用滞环控制，建模过程较为简单，不再受限于开关频率。文献［12-13］提出了一种定频调制方法，通过动态改变滞环比较的宽度来调整开关管的开关频率，可以实现开关频率固定，但该方法动态环宽的计算过程要求系统参数不变，在负载突变的情况下则易失去稳定，不仅不能保持开关频率的恒定，甚至会增加输出电压的谐波范围，因此，定频调制也有一定的局限性。针对此问题，文中提出一种定环宽的电压滞环控制方式，该方法动态性能好，不易受外界干扰；另外，虽然通过缩小滞环宽度可以减小输出电压的谐波畸变率，但业内一直未将滞环宽度与谐波畸变率之间的关系进行量化分析，为此，将进一步研究定环宽条件下滞环宽度与谐波畸变率之间的关系，给出其函数关系分析式。

1 单相半桥逆变拓扑

图1所示为常见的单相半桥逆变电源拓扑，电源通过开关管Q1、Q2及L-C滤波器向负载供电，负载一侧接开关管中点，另一侧接至电源中性点，上桥臂与下桥臂不同时导通。

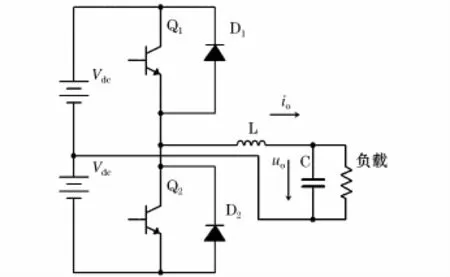
图1 单相半桥逆变拓扑Fig.1 Single-phase half bridge topology

控制器通过电感反馈的电流值io和电容反馈的电压值uo控制开关管Q1、Q2的导通与关断。下面具体分析了该逆变拓扑的五种工作模式。

图2 单相半桥逆变拓扑工作模式Fig.2 Working mode of single-phase half bridge inverter topology

模式Ⅰ：如图2（a）所示，上桥臂Q1导通，下桥臂Q2关断，电源向L-C滤波器及负载提供正电压，电流表达式满足：

模式Ⅱ：如图2（b）所示，上桥臂关断，下桥臂未导通时，电流由于电感作用并不会立刻为零，由反并联二极管D2提供续流通道，电感通过负载即二极管向电源回馈电能，直至电流为零，二极管D2截止。

模式Ⅲ：如图2（c）所示，上下桥臂均未导通，且电感电流为0时，由并联在负载上的电容向负载放电，此时的电流表达式满足：

模式Ⅳ：如图2（d）所示，下桥臂Q2导通，上桥臂Q1关断，电源向L-C滤波器及负载提供负电压，电流表达式满足：

模式Ⅴ：如图2（e）所示，下桥臂关断，上桥臂未导通时，电流由于电感作用并不会立刻为零，由反并联二极管D1提供续流通道，电感通过负载即二极管向电源回馈电能，直至电流为零，二极管D1截止。

19世纪末，俄罗斯音乐达到了前所未有的高度，即使是现在，当我们低头缅怀前面所提及的音乐家们时，在内心深处却会情不自禁地抬头仰望他们高大的身影。当人类历史进程走进20世纪的时候，一方面新古典主义宣称要避开现实世界的纷扰，回到巴赫甚至是比巴赫更远的年代，而另一方面，印象主义则跃跃欲试地另辟蹊径，大胆改革创新，意欲创造一个全新的音乐理念和风格，并使自己成为繁荣百年的浪漫主义音乐的终结者。然而，无论是鼓噪一时的新古典主义，还是风靡一时的印象主义，都无法抵消浪漫主义音乐，特别是19世纪俄罗斯音乐在人类音乐文化史上的辉煌成就和深远影响。

2 恒定滞环宽度的控制策略

恒定滞环宽度的电压滞环控制策略，旨在让负载输出电压在参考电压正负偏差一定宽度的范围内波动，通过限制负载输出电压的波动幅度来减小输出电压的谐波畸变率。控制策略中，参考电压的正误差滞环与负误差滞环宽度相同，负载输出电压在参考电压误差滞环宽度内，开关管均不动作；而当负载输出电压超出参考滞环比较带时则控制器控制相应开关管导通。

如图3所示，uo为输出电压，G1、G2为开关管Q2、Q1触发信号。当负载输出电压低于参考电压负误差滞环时，开关管Q1导通，Q2截止，给负载正电压，使逆变器工作在模式Ⅰ下，拉升负载输出电压，直至负载输出电压重回参考电压误差滞环比较带时，开关管Q1关断，逆变器工作在模式Ⅱ及模式Ⅲ；而当输出电压高于参考电压正误差滞环时，开关管Q2导通，Q1保持截止，电源给负载负电压使输出电压降落至参考电压偏差带，逆变器工作在模式Ⅳ下，直至电压回到误差滞环比较带时，开关管Q2截止，逆变器工作在模式Ⅴ及模式Ⅲ。需要指出的是，逆变电源实际输出电压并不会被限制于控制滞环内，控制滞环仅为控制器的控制提供参考，实际的输出电压偏差滞环会略宽于控制滞环。

图3 电压滞环控制示意图Fig.3 Schematic diagram of voltage hysteresis loop control

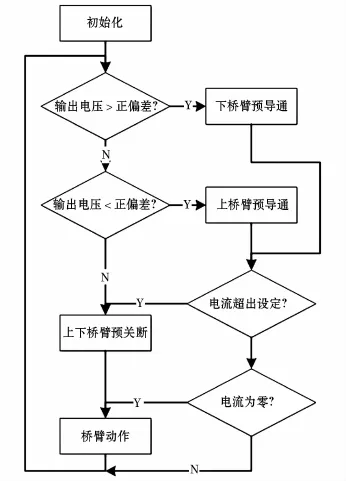
图4 恒定滞环宽度的电压滞环控制策略流程框图Fig.4 System structure block diagram of constant hysteresis bandwidth voltage hysteresis control

控制器的逻辑框图如图4所示。为了逆变器的安全运行，逆变器控制器为输出电流设定限幅，负载电流一旦超过设定限幅值则开关管Q1、Q2关断，并持续至电流恢复至限幅范围以内，才能继续控制开关管的开通，否则将一直保持开关管Q1、Q2的关断状态。为降低开关管的开通损耗，在控制器判断开关管Q1、Q2导通时，将控制逻辑暂存，并通过串联在负载上实时反馈的电流检测模块判断开关管是否具有零电流开通的条件，若负载电流为零，则控制器将暂存的状态输出，开关管开通，若电流不为零但尚未超过电流限幅值，则保持开关管的状态不变。

3 仿真分析

3.1 基于Stateflow的MATLAB/SIMULINK模型建立

文中使用MATLAB/SIMULINK软件建立仿真模型，以Stateflow作为控制器控制开关管的开关及相关控制信号的输入。MATLAB/SIMULINK的图形化操作模块Stateflow有限状态机（finite statemachine），通过图形化编程界面将C语言内嵌于其中，可对未含有语法错误的程序块进行编译进而生成可供MATLAB/SIMULINK执行的S函数模块。仿真界面如图5所示，控制器通过采集负载输出电流电压值与参考电压误差滞环值比较，控制开关管Q1、Q2的通断。在Stateflow触发端引入触发信号以模拟实际运行环境中单片机/DSP等控制器的晶振周期，每当Stateflow的触发信号来时控制器才对控制状态进行运算控制，仿真参数如表1所示。

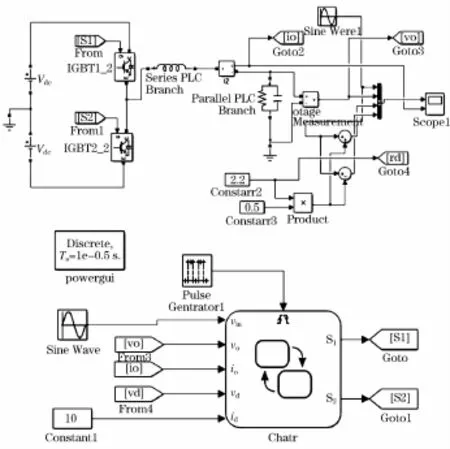
图5 基于Stateflow的MATLAB/SIMULINK仿真模型Fig.5 MATLAB/SIMULINK simulation model based on Stateflow

表1 仿真模型参数Tab.1 Simulation model parameters

3.2 仿真结果

在输出电压的±10%、±5%、±2%、±1%偏差内设置误差滞环带（即相应误差值vd为22 V、11 V、4.4 V、2.2 V），如图6、图7所示，从图中可见波形畸变随着偏差的增加而变大。从图8中可以看出，控制器在实现开关管零电流开通的前提下实现了对输出电压良好的滞环控制。

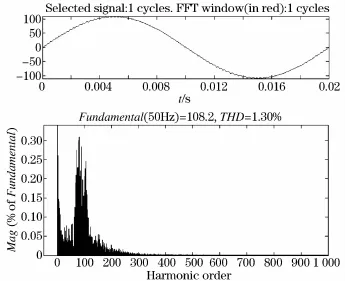
图6 滞环宽度为±1%负载输出电压波形及谐波分析Fig.6 Waveform and harmonic analysis of the load output voltage of the±1%hysteresis bandwidth

为了进一步研究滞环宽度与谐波畸变率之间的关系，对输出电压偏差±1%～±10%每隔±0.25%取样，可得如图9所示的散点，由图可见散点有线性化的趋势，对散点进行线性化拟合，得到直线：THD（%）＝42.284 5x＋0.587 3；其中 THD（%）为负载输出电压谐波总畸变率，x为人为设定的输出电压滞环宽度在输出参考电压幅值中的占比；线性拟合优度R2＝0.993 53；可见滞环宽度与总谐波畸变率之间具有高度线性相关性。

图7 ±10%、±5%、±2%、±1%滞环宽度输出电压波形Fig.7 Output voltage waveform of±10%，±5%，±2%，±1%hysteresis bandwidth

图8 ±1%滞环宽度输出电压电流波形图Fig.8 Output voltage and current waveform of±1%hysteresis bandwidth

图9 ±1%～±10% 滞环宽度-谐波畸变率散点及线性拟合图Fig.9 Total harmonic distortion and linear fitting of±1%～±10%hysteresis bandwidth

4 结束语

提出了一种恒定滞环宽度的逆变电源电压滞环控制方式，并使用软开关控制开关管的开通，以单相半桥逆变电源为例，在MATLAB/SIMULINK上建立了仿真，研究了恒定滞环宽度与输出电压谐波畸变率之间的关系。仿真结果表明，该控制方式可以使输出电压在电压控制滞环内良好的跟踪参考电压，滞环宽度越窄，开关器件的开关频率越高，输出的波形畸变率越小，输出越接近正弦波。在滞环宽度±1%～±10%变化范围内，滞环宽度在参考输出电压中的占比x与逆变器负载输出电压谐波总畸变率THD（%）之间存在THD（%）＝42.284 5x＋0.587 3的函数关系。