基于电压源换流器的高压直流输电系统控制研究*

黄政，吴杰

（1.贵州理工学院 电气与信息工程学院，贵阳550003；2.上海交通大学 电气工程系，上海200240）

0 引 言

随着智能电网、分布式发电技术以及高压直流输电技术的快速发展，基于电压源换流器的高压直流输电技术（VSC-HVDC）受到了广泛的关注和研究。它作为新一代直流输电技术，采用了全控电力电子器件，能够灵活的独立控制有功功率和无功功率，克服了以往直流输电系统中的换相失败、必须连接于有源网络等缺点，在大功率远距离输电方面具有诸多不可替代的优势，从实际工程运行来看，它在可再生能源并网、偏远地区供电、异步交流电网互联等领域有着广阔的应用前景［1-4］。

由于VSC-HVDC是具有强耦合、多变量的非线性系统，对其数学模型需进行线性化和解耦控制。近年来，将反馈线性化思想引入到变流器控制中进行研究的大多为系统的三阶状态方程，分别是控制有功分量id，控制无功分量iq，控制直流电压udc。而将反馈线性化思想应用于电压源直流输电变流器控制的文献还较少。文章结合VSC-HVDC系统在dq坐标系下的状态方程，两侧的变流器采用id、iq作为状态变量对系统进行反馈线性化的设计，线性化过程中不会忽略任何高阶非线性项，实现对dq轴电流的解耦控制。利用Matlab/Simulink软件建立仿真模型，验证了该控制方案的有效性。

1 VSC-HVDC结构和数学建模

两端VSC-HVDC输电系统的典型结构如图1所示，主要包括多台风机构成的一个风电场、两端VSC换流站、高压直流输电电缆、换流电抗器、交流变压器等。

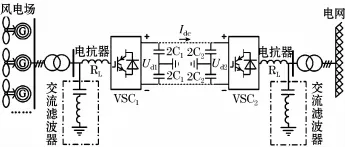
图1 风电场VSC-HVDC并网输电系统结构图Fig.1 VSC-HVDC grid-connected transmission system for wind farms

由图1可得VSC-HVDC系统三相静止坐标系下的数学方程：

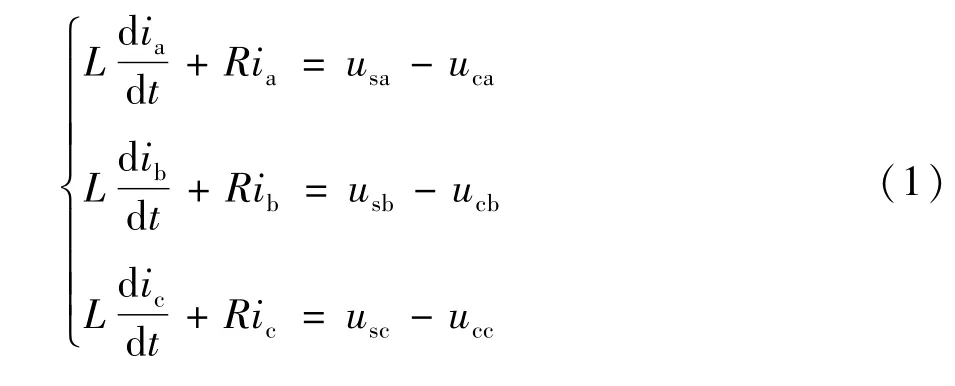
式中 usa，usb，usc为交流系统输出电压；uca，ucb，ucc为VSC换流器输出电压；ia，ib，ic为交流系统输出电流，由于两端交流系统对称运行，对式（1）进行

PARK变换，式（2）为变换矩阵P。

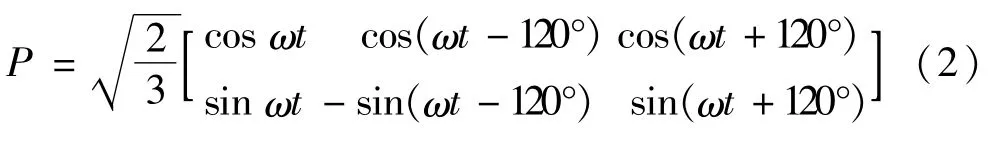
可得dq坐标系下数学模型：

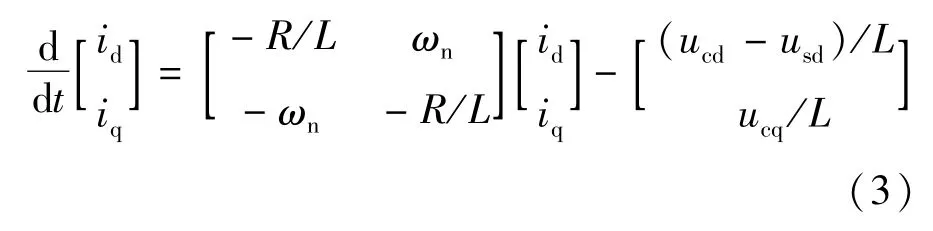
式中 ωn代表交流电压角频率；id、iq为系统两端线路交流电流d，q轴的分量；usd，usq表示系统两端交流电压d，q轴的分量；ucd，ucq为变流器交流端d，q轴的电压分量；当d轴定位于电网电压矢量，则usq＝0，usq＝US（US代表电网电压空间矢量幅值）。变流器交流端的有功、无功功率以及直流端的有功功率为：

2 反馈线性化方法

对于如下的多输入—多输出的系统跟踪控制［5-6］：

式中 x是n×1的状态向量；u（其元素是ui）是m×1的控制输入向量；y代表m×1的输出向量，其元素用yi表示；G是n×m的矩阵，矩阵G的列为光滑向量场gi；f为光滑向量场；h为光滑向量函数。通过对系统输出进行微分，当输入出现可得到输入—输出的线性化关系。设使得在y（ri）i中至少出现一个输入的最小整数为ri，则有：

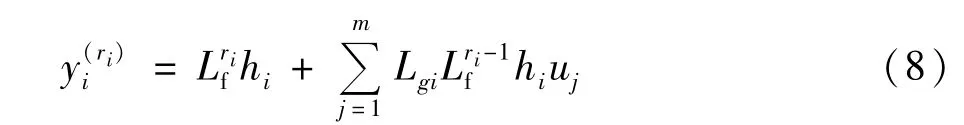
式中 Lf为沿向量场f（x）的李导数；Lg是g（x）沿向量场f（x）的李导数。在x0的一个邻域Ωi中存在至少一个 j，使得 LgjLri－1jhi（x）≠0。可得［7-8］：

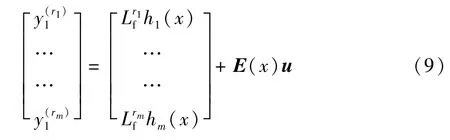
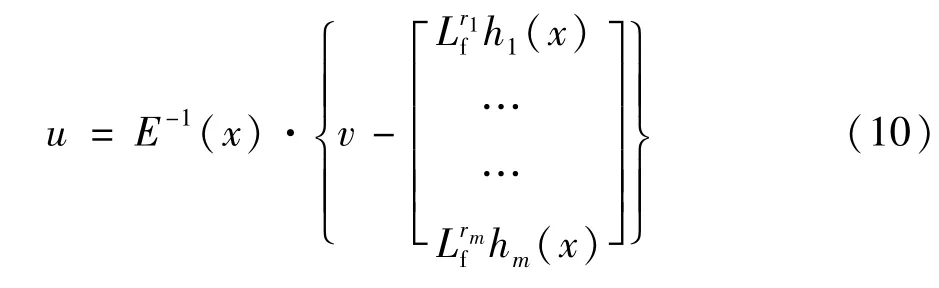
3 换流器的非线性控制

将变流器的动态数学方程式（3）写为式（6）的形式，可得到：

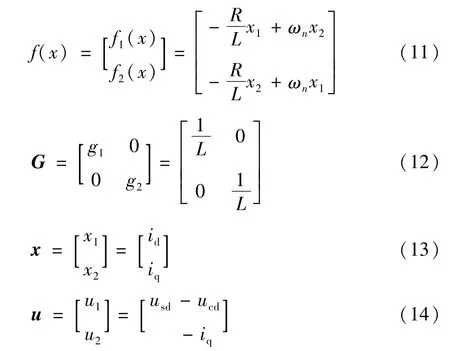
选择系统输出为：

运用反馈线性化法，对输出y1，y2微分直到至少出现一个输入，并将其写成式（10）的形式［9］为：

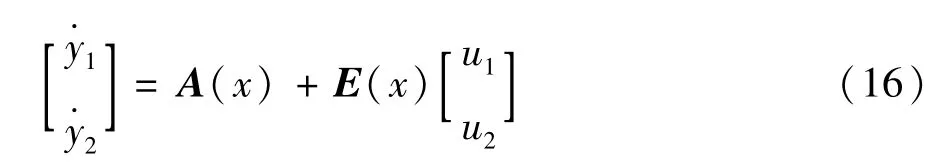
矩阵E（x）非奇异，则系统的控制输入为：

根据有界跟踪定理［8］，考虑到系统中运行扰动会有跟踪误差产生，因此加入积分项得到系统等价的输入 v1、v2为：

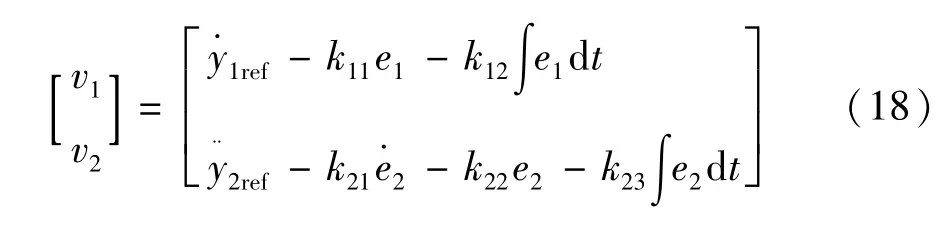
式中 e＝y－yref，因此误差的动态方程为：

当 t→∞时，e→0［10］。将式（18）带入式（17）可得：

换流器dq轴控制信号分别为：

因此，换流器电流内环的非线性控制结构如图2所示。

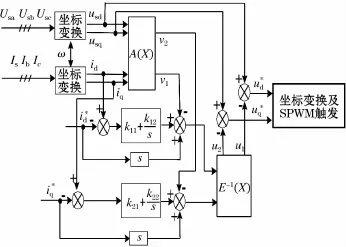
图2 换流器非线性控制原理图Fig.2 Schematic diagram of converter nonlinear control

4 仿真与分析

为验证所提出的控制方案的有效性和正确性，文章利用 Matlab/Simulink软件构建风电场 VSCHVDC系统进行仿真研究。其中，VSC1采用定直流电压和无功功率，VSC2为定有功功率和定无功功率的控制方式。其主要参数为：换流电抗器L1＝L2＝24.1 mH，相应的等效电阻损耗 R1＝R2＝0.076Ω，交流系统额定电压Us1＝Us2＝100 kV，直流侧额定电压200 kV，直流侧电容C1＝C2＝0.08μF，直流线路等效电阻0.075Ω，等效电感16 mH。采用SPWM触发方式，开关频率1 350 Hz。设置直流电压调节器：kp1＝3.5，ki1＝20.5；有功功率调节器：kp2＝2.47，ki2＝15.8；无功功率调节器：kp3＝0.85，ki3＝20。

系统启动后进入稳态的波形如图3所示。其中图3（a）是直流电压响应曲线，可见反馈线性化法设计的控制器在系统启动过程中动态性能良好。图3（b）和图3（c）是两端变流器a相电压和电流的波形，从图可见，两端电流电压波形分别为同相位和反相位，系统运行在单位功率因数下。图3（d）是有功、无功功率响应波形，可见系统启动平稳，具有较高的跟踪精度。

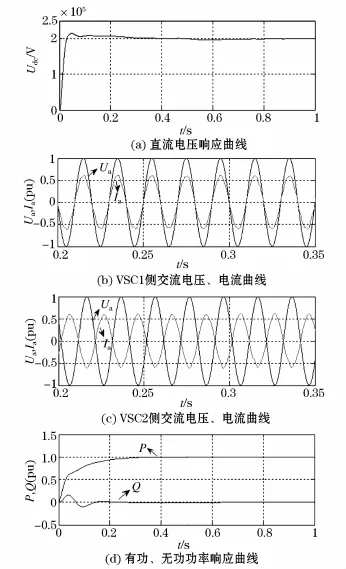
图3 VSC-HVDC系统稳态仿真结果Fig.3 Steady state simulation results of VSC-HVDC system

图4为交流系统暂态过程响应曲线，仿真中设置电网在 t＝0.5 s时发生三相对地短路故障，在t＝0.6 s时恢复正常。其中图（a）是有功、无功功率响应的波形，图（b）为直流电压响应波形，暂态过程中直流电压仅出现小幅波动，故障恢复后能迅速的跟踪给定，有较强的抗干扰能力。

图4 电网故障时VSC-HVDC系统仿真结果Fig.4 Simulation results of VSC-HVDC system during the grid failure

5 结束语

针对VSC-HVDC系统多输入—输出、非线性、强耦合的特点，文章建立了VSC-HVDC基于dq坐标系的数学模型，在双闭环传统控制方式中，采用反馈线性化方法设计了内环电流控制器，提高了系统的动态响应特性，通过对系统稳态和故障工况的仿真分析，验证所设计控制方案的有效性和可靠性。