基于振动分析法的变压器故障分类和识别*

夏玉剑，李敏，陈果，石同春，沈大千，王昕

（1.上海交通大学电工与电子技术中心，上海200240；2.国网四川省电力有限公司广安供电公司，四川广安638500）

0 引 言

在电力系统的各种设备中，变压器是昂贵且重要的电力设备，其运行状态的可靠性是电网安全运行重要保障。统计表明，变压器发生故障较多的部件是其绕组和铁芯，此类故障事件在变压器总事故中所占比例达到70%［1］。因此，迫切需要一种可以准确判断变压器绕组和铁芯运行状态的方法。

目前，检测变压器运行状态的方法日益增多。文献［2-3］提出了短路阻抗法，在离线状态下，测量变压器绕组的阻抗值，分析其阻抗值变化，诊断绕组变形程度，但该方法灵敏度低、可靠性差。低压脉冲法提高了变压器绕组检测的灵敏度，但该方法主要应用于现场试验测试，并且该方法具有在现场测量中易受外部干扰、需多次校正、而且测试过程中通过特殊布置电路以确保试验的重复性等缺陷［4］。在此基础上，文献［5-6］采用频响分析法，通过测量变压器三相绕组的频率响应曲线检测变压器绕组变形程度，消除了低压脉冲法存在可重复性差的缺陷，但该方法只能对变压器进行离线检测。为此，文献［7-8］利用振动分析法，在理论和试验中，证实振动分析法的带电检测有效性，并具有较高的灵敏度，但无法实现对变压器故障类型的定量化诊断。文献［9-11］提出利用希尔伯特能量谱及边界谱分析变压器振动信号的特征，在一定程度上定量化判断变压器绕组和铁芯故障类型，但该文献并未实现对变压器绕组和铁芯故障类型的直观分类，无法通过变压器振动信号对变压器故障类型进行故障识别，给出相应的故障诊断。

为此，提出一种基于主成分分析（Principal Component Analysis，PCA）和 K近邻法（K-Nearest Neighbor，KNN）分类识别的变压器故障检测方法。首先，利用集合经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）方法对试验所得的变压器正常工况、绕组变形、铁芯故障三种状态下的振动信号进行特征矢量提取。然后，再对特征矢量进行主成分分析处理，将多维的特征矢量投影到二维图像中，实现直观地故障分类同时为分类识别提供帮助，并用KNN进行分类识别，实现对变压器状态的直观故障分类和故障识别。最后，通过对变压器试验数据进行分析，可知该方法能实现对变压器正常状态、绕组变形、铁芯故障三种状态直观分类，并能对测试样本进行快速自动模式识别，准确判断测试样本的变压器故障类型。

1 振动信号及特征值提取

1.1 振动信号

在变压器运行中，变压器主要的振动来源是变压器的绕组和铁芯。

变压器运行中，电流流经变压器绕组，在其周围会产生漏磁场。在绕组电流和漏磁场共同作用下，绕组内部将产生电动力，并随着负载电流增大而增大。绕组中振动信号与负载电流的平方成正比，即：式中Fw为绕组在电流和漏磁场中产生的电动力；i为负载电流。

在变压器的铁芯中分布正弦交变的电磁场，交变磁场引发硅钢片振动。大量研究表明，铁芯振动主要由硅钢片的磁滞伸缩引起，而铁芯振动的信号与变压器电源电压的平方成正比，即：

式中Fc为铁芯在交变磁场中所受电磁力；U为电源电压。

由式（1）、式（2）可知，变压器的绕组和铁芯的振动信号可以反映出变压器的运行状态，通过检测振动信号，提取振动信号的特征矢量，可以诊断出变压器的运行状态。

1.2 振动信号的特征矢量提取

由于变压器绕组和铁芯结构存在非线性，变压器振动信号也会呈现出比较明显的非线性特性。传统的时频分析方法在分析非线性非平稳信号时存在不足，因此文章采用适用于非线性、非平稳信号处理的希尔伯特-黄变换［12］。

Huang提出的EEMD方法通过人为加入白噪声，为信号分解提供相对均匀的尺度分布，然后进行经验模态分解，获取不同尺度的频率区域下振动信号的本征模函数（IMF），并对其进行希尔伯特分析，得到瞬间频率和瞬间幅值，将它作为特征矢量，具体过程如下。

（1）向原始信号x（t）中加入N次的白噪音序列ni（t），（i＝1，2，…，N），即：

（2）对 Xi（t）分别进行经验模态分解，得到各个IMF分量和余量，即：

式中hij为分解后第j个IMF分量；rin为分解后的余项；n为分解层数。

（3）分解得到的各个IMF的分量：

式中hij（t）表示对原始信号进行EEMD分解得到的第j个IMF分量；N为加入白噪声的次数。

（4）选取每个IMF分量进行希尔伯特分析，并对相对应下的幅值构成特征矢量V：

式中Aj（i）为第j个IMF分量的振幅。该特征矢量V能够综合表征变压器的状态信息。

2 主成分分析和KNN分类识别

2.1 主成分分析

主成分分析是在多维模式空间中利用样本矢量的位置分布，以样本矢量的最大方差方向作为判别矢量，重新组合成一组不相关的特征矢量代替样本矢量［13］。文中利用EEMD提取变压器振动信号在正常状态、绕组故障、铁芯故障三种运行状态下的特征矢量 V＝［v1，v2，…，vz］。同时针对三种运行状态，各选择m组作为经验样本，得到3m×z的训练矩阵R。

对训练矩阵R根据式（8）做中心化处理得到矩阵 A＝［aij］，且：

式中aij是R中元素中心化后的数据；i是训练矩阵R中每行的均值。

利用式（9）计算协方差矩阵S。

计算S的特征值和特征矢量，将特征值进行排列，选取前两个最大的特征值，找到其特征矢量［α1，α2］。

对 R进行式（10）所示的［α1，α2］方向的投影转换，得到训练样本的二维图。

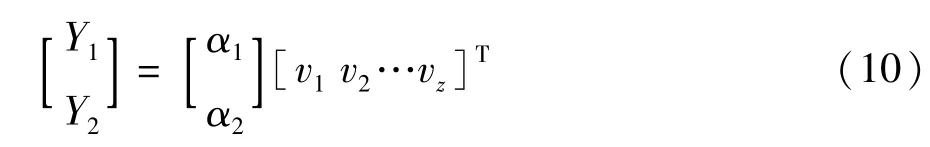
式中Y1、Y2分别为二维投影的横、纵坐标。通过主成分分析法将变压器振动信号在正常状态、绕组故障、铁芯故障三种运行状态的特征矢量投影到二维图像中，直观地实现故障分类，更有助于快速模式识别。

2.2 KNN分类识别

K近邻法的核心思想：在特征空间中，一个样本有K个最相邻的样本，其中K个相邻样本中多数属于某一个类别，则该样本属于这个类别［14］。设变压器运行状态下的特征矢量中测试样本为Vt＝［v1t，v2t，…，vzt］，经过主成分分析得到相应的向量为Yt＝［yt1，yt2］，计算测试样本和每个样本的距离，为：

将计算出的距离按大小降序排列，选择距离相对小的K个样本作为测试样本的K个近邻。设在K个样本中，来自w1、w2、…、wc状态类型的相应样本数有 k1，k2，…，kc个。则定义判别函数为：

决策规则为：若 gj（Vt）＝max（ki），则测试样本Vt∈ωj。即测试样本Vt对应的变压器的运行状态为wj状态类型。

3 变压器表面振动信号采集及分析

为验证上述基于主成分分析和KNN分类识别的变压器故障检测方法，本试验利用四川某公司的110 kV三相变压器获取的振动数据进行了分析研究。试验中，在同一电压、同一电流环境下（其中包括变压器风机都不工作、油温相同等外界环境），分别选择处于正常状态、绕组变形、铁芯故障三种状态的变压器，采集变压器的振动信号。采集信号过程中，将三个振动加速度传感器经永磁体底座固定在变压器高压侧箱壁上，采样频率为25.6 kHz，振动信号现场采集如图1所示。

图1 振动信号的现场采集Fig.1 Vibration signal acquisition in the field

试验所采用的传感器为CT1005LC型号的IEPE工业振动传感器，其具有抗电磁干扰、信噪比高、方便安装等优点，其主要技术参数见表1。

表1 CT1005LC主要技术参数Tab.1 Main technical parameters about CT1005LC

3.1 提取特征矢量

为了能识别变压器故障类型，将EEMD应用于变压器正常状态、绕组变形和铁芯故障下的振动信号分析，同时分别提取变压器振动信号的特征矢量V＝［v1，v2，v3，v4，v5，v6］，其中变压器正常状态的结果如表2、图2所示。

图2 正常状态下振动信号的IMF分量Fig.2 Vibration signal IMFs in normal state

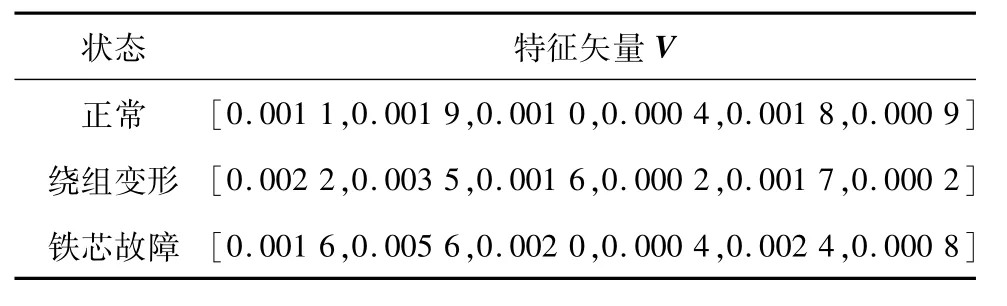
表2 变压器三种工况下的特征矢量Tab.2 Feature vectors of transfomer vibration signal for three states

由表2可知，在不同状态下，相同频率段对应的特征矢量数值不同，因此，有利于识别变压器的不同故障类型。

3.2 主成分分析和KNN分类识别

在三种不同状态下各选择90×3＝270组振动信号特征矢量作为经验样本。首先对得到的特征矢量进行主成分分析处理，得到直观的二维图形，如图3所示。

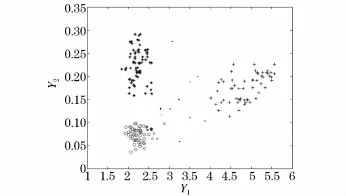
图3 经验样本的主成分分析Fig.3 Principal component analysis of empirical samples

由图3可以直观地看出变压器振动信号在正常状态、绕组故障、铁芯故障下的特征矢量所对应的投影点，虽然其中有几个散点，但是整体上具有很好的聚类效果，聚类比例达到96.3%。因此，此分类方法效果较好。

在以上测试结果基础上，再选取21组未知类型振动信号作为测试样本，测试时选择 K＝9，利用KNN识别法对变压器振动波形进行分类识别，其测试样本结果如图4所示，图中五角星表示测试样本。

由图4实验结果可明显看出，其中有7组信号属于变压器正常状态，7组信号属于绕组故障状态，6组信号属于铁芯故障状态，其中1组为散点，分类识别正确率为95.2%。因此，本方法可很好地识别测试样本对应的变压器状态，直观、有效地判断变压器运行状态。

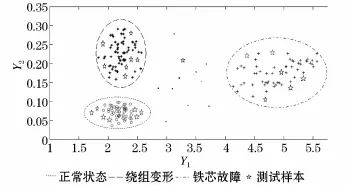
图4 KNN分类和测试识别Fig.4 KNN classification and fault identification

4 结束语

基于主成分分析和KNN分类识别方法，对变压器振动波形的特征矢量进行分类和识别，从而直观有效地判断变压器的运行状态。

（1）采用EEMD对变压器的振动信号行分析，提取变压器运行中正常状态、绕组变形、铁芯故障三种不同状态下的振动信号的特征矢量；

（2）采用主成分分析法对振动信号提取的特征矢量进行降维分析，直观地将特征矢量投影到二维图形中；

（3）采用KNN分类识别方法对样本数据进行分类，试验表明该方法对变压器正常状态、绕组变形、铁芯故障三种状态分类效果明显，很好地实现了对测试样本的模式识别，并准确判断出测试样本变压器的运行状态。