有限元和有限体积法结合的油浸式变压器温度场计算方法*

王伟，魏菊芳，王楠，王巨伟，王永强

（1.国网天津市电力公司电力科学研究院，天津300384；2.华北电力大学河北省输变电设备安全防御重点实验室，河北保定071000）

0 引 言

大型电力变压器构造复杂，内部的传热机理也很难分析清楚，对于整个变压器绕组的内部温度绕组热点温度特别是准确的预测是非常困难的［1-5］。目前，主要由有两种方法来对油浸式变压器温度场进行模拟计算。一是建立变压器热路模型计算［6-16］；再是采用数值计算方法和使用计算机模拟程序进行辅助计算［17-26］。而这其中，利用数值计算方法对于变压器温度场分析方法目前主要有两种，一是基于有限元法对变压器进行二维或三维的仿真计算分析［17-22］；二是基于有限元方法改进的有限体积法进行仿真计算［23-26］。然而，计算结果表明，这两种方法的误差都比较大，要准确地计算变压器的温度分布，处理变压器内部温度场，需要提出一种改进的方法。

油浸式变压器的损耗分为负载损耗和空载损耗。损耗使绕组和铁心发热，温度上升，并与变压器绝缘油之间进行对流传热。变压器油受热向上运动，受冷又向下流动，油循环流起来，透过散热器和油箱，将热量分散到外部。

基于有限元或有限体积模拟的方法，对变压器三维模型划分网格。由于绕组和铁芯的结构是相对固定的，它是由固体金属组成，有限元法具有更好的效果。变压器油属于液体部分，流体结构不定，正有利于有限体积法发挥其优点。

1 变压器内部热传递过程及计算方法分析

1.1 变压器发热机理分析

变压器总损耗可以表示为：

式中PT为变压器的总损耗；PNL为空载损耗；PLL为负载损耗，这其中，负载损耗可分为直流损耗（Pdc=I2Rdc）和杂散损耗。而杂散损耗也可分为涡流损耗和其他部件的杂散损耗。其他杂散损耗是指其他部位的损耗，如变压器附件、变压器油箱等部分的损耗。负载损耗PLL可以表示为：

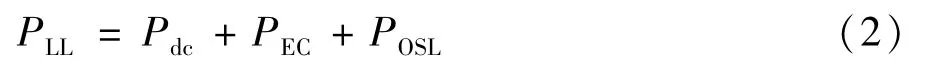
式中Pdc为绕组电阻发热带来的损耗；PEC为绕组涡流损耗；POSL为变压器附件、油箱等部位的其他损耗；杂散总损耗PSL可以通过从负载损耗PLL中减去中直流损耗Pdc得到：

空载损耗可表示为［5］：

式中P1为铁心的磁滞损耗，W；P2为铁心的涡流损耗，W；δh为磁滞损耗系数；δe为涡流损耗系数；f为电流频率，Hz；Bm为磁通密度的最大值，Wb/m2。由于硅钢具有的磁化饱和特性，所以在变压器负载电流增大时，Bm随负载电流的增加并不明显。

负载损耗可表示为：

式中I2R为绕组热效应损耗，其值大小由负载电流以及绕组线圈的电阻值确定，W；PW为绕组中的涡流损耗，W；Pz为杂散损耗，W。目前没有很好的方法可以计算绕组中的杂散损耗或涡流损耗，常用的方法是上述的经验计算方法。

1.2 变压器内部的热量传递过程

油浸式变压器运行时，其负载损耗和空载损耗导致绕组和铁心等金属构件温度升高，金属具有较高的导热系数，使绕组铁心等金属构件温度迅速升高。在绕组和铁心内部产生的热量传导至金属外部，之后热量由于传导效应传导至到温度相对较低的绝缘油中。热量传至油中使其温度上升，密度变小，较轻的热油从下向变压器油箱上部分移动，当热油经过油箱顶部、散热片和油箱壁，由于低温环境的冷却，再向下部流动，当温度降低了的油再次经过绕组和铁心时，就形成了循环，将产生的热量由内部传递到外部。当运行中的变压器产热热量和散热热量相等时，便处于了热平衡的稳定状态。

此时，变压器运行时热量的产生和传导主要分为以下几个过程：

（1）热传导过程：器身的金属构件，铁心和绕组由于存在损耗产生热量，热量在金属内部传导。这个过程是金属的产热和导热过程，且构件内部无相对运动；

（2）热对流过程：当热量传递到金属表面时，高温金属与温度较低的油由于存在温差会进行对流换热，使油的温度上升；

（3）加热后的变压器油在油箱和散热片内部产生流动，并且传递一部分热量给油箱和散热片；

（4）由于散热器和油箱的温度比外部空气高，二者同时将热量传递到外部。

1.3 变压器内热传递分析方法原理

由以上分析可以看出，过程（1）为金属构件导热，对此过程计算的精准度对之后的导热传热过程的影响很大，对过程（1）的计算应尽量保证精确。因此过程（1）的计算应使用有限元法计算。

过程（2）～过程（4）是变压器油参与的传导过程，有限元方法对于有流体参与的过程的处理效果不如有限体积法。由于变压器油形状不定，且有限体积法相对有限元法，对网格质量的要求较低。故过程（2）～过程（4）应用有限体积法进行计算。

因此，对铁心和绕组部分的金属传热过程（1），用精确度较高的有限元法计算。对于流体参与的过程（2）～过程（4），采用效果更好的有限体积法计算更为合理。

2 利用有限元法计算绕组和铁心的热传导

2.1 有限元法在变压器绕组和铁心热传导计算中的优势

有限元方法的基础是变分原理和加权余量法，其基本思想是将计算区域划分为有限个互不重叠的子块，在每一个单元中，选择一定数量的节点作为一个函数的计算插值点，变线性表达式的微分形式和修正的节点的每个变量或其衍生价值选择的插值函数，基于变分原理和加权余量法，转化为对微分方程的求解［21-22］。

有限元法（FEM）在处理区域形状较复杂的流体流动问题时，其效果不如有限体积法（FVM）。但有限元法对与金属和固态的部分计算精度较高，变压器中绕组和铁心部分是固体结构，并且几何形状规则，应使用有限元法进行高精度的导热过程计算。

2.2 绕组铁心的单元选择和网格划分

在油浸式电力变压器中，绕组与铁心的发热是变压器内热量的主要来源。在绕组和铁心的计算中，选择精度较高的三维8节点实体单元进行计算。绕组和铁心中各个网格单元的导热量都能作为单元的面载荷输入，以此构建导热矩阵。由于绕组和铁心具有很规则的结构，故对其网格的划分可以采用高精度的Sweep划分方法，在尽量节省时间的同时，保证计算结果的准确性。

2.3 利用有限元法模拟绕组和铁心的热传递过程

绕组和铁心的热传导过程过程遵循如下的能量守恒方程：

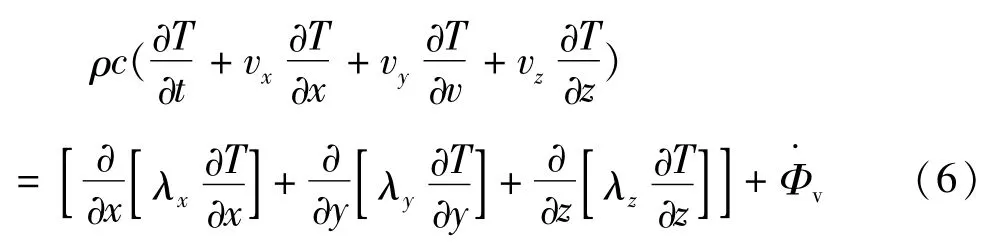
式中 ρ为金属的密度；c为比热；vx、vy、vz分别为沿着各坐标的速度分量；λx、λy、λz分别为沿着各坐标的导热系数。Φ·v为单位体积的生热率。当变压器处于温度恒定的稳定运行时，上式可简化为：

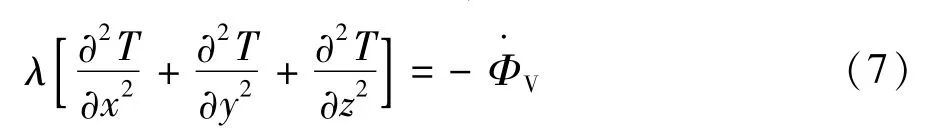
式中 λ为沿着各坐标的导热系数；Φ·V为单位体积的生热率。

在带入绕组和铁心的产热情况时，将其等效为均匀发热的发热体，产热的总量一定，单位时间内热源单位体积产热量固定：

式中p为变压器的总体损耗；V为热源的体积。

2.4 求解方法的选用

有限元求解方法中，比较常用的有5种。通过比较这几种方法的精度、资源占用、运算速度等因素，选用预条件共轭梯度法（The Preconditioned Conjugate Gradient Method）。这种方法的自由度可以达到5×105，对于某些网络结构，自由度甚至可以更大，对具有精细网格的实体模型的求解优势明显。预条件共轭梯度法通常只需要其他算法所需资源的3/4左右，利用与条件共轭梯度法运行大量网格模型或进行精确计算时，相比其他算法效率更高。故采用预条件共轭梯度法可以精确地求解变压器绕组和铁心的内部导热。

3 有限体积法计算流体部分温度场

3.1 FVM在流体模拟仿真中的计算原理

有限体积法（FVM）又被称为控制体积法。其基本思路是将求解区域划分为大量不重复的控制体积，并使每个网格点周围控制有一定的体积，将待解的微分方程对各个控制体积做积分运算，便得出一组所有控制体积的离散方程［28-29］。

利用有限体积法对油流体的传热过程的计算中，温度场和流速场的通用方程为：

式中 φ代表某一个变量；Γφ、Sφ分别为对应的扩散系数项和广义源项：ρ为流体密度；U为流体运动速度矢量；div（ρUφ）、grad（φ）分别为对应特定变量的散度和梯度。

3.2 有限体积法求流体传热的过程

FVM是将控制流动传热的非线性偏微分方程，通过解相应的流体控制单元的线性方程组，从而得出所求网格控制点上流场物理量变化值，即系统流场的解。由于系统所加压力不变，利用压力耦合方程的SIMPLE算法求解，利用半隐式求解算法解决了控制方程。其计算的步骤如下：

（1）由压力场初值，求解速度场初值，得到流体的初始速度v0；

（2）通过修改压力场、求解微分方程，得到压力的修正值，令修正值对应的速度场可以达到本次迭代的连续方程约束条件，将动量方程的压力和速度的约束关系代入本次迭代的连续性方程，得到压力值的修正方程，从而得到本次迭代的速度修正值vm0；

（3）根据校正后的压力场p=p0+pro，求解速度场v=v0+vm。并确定压力场的结果是否满足收敛条件，如果条件满足便终止计算，若不满足收敛条件，返回步骤（1）继续计算流程。

3.3 FVM计算变压器中油参与的热传导

在前面所述的过程（1）中，铁心发热和导热遵循傅里叶对流换热定律：

式中λ是导热系数；h为换热系数；tw为金属温度；tf为流体温度。

当外部环境温度不变化时，变压器的铁心和绕组的发热量也是不变的，变压器的发热量和散热量相抵消，变压器温度达到平衡点。在这个时间点，在式（11）中给出了内温度场和流场的方程组。

变压器达到热平衡状态时，变压器油的非齐次边界条件为：

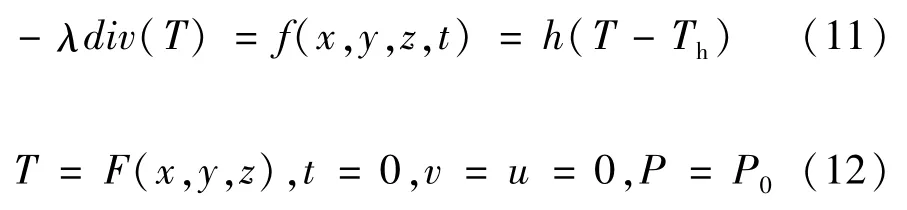
式中λ为流体的热传导系数；T为关于空间变量（x，y，z）与时间变量 t的函数；F（x，y，z）为变压器发热与散热过程的初始约束函数，f（x，y，z，t）是变压器与外界换热的约束函数，h为换热系数；P=P0为初始时刻的微元所受压强。

4 利用混合方法计算变压器温度场

4.1 两种方法的比较与结合

对于相同网格密度下，采用有限体积法的结果要稍优于采用有限元法计算得出的结果，但都存在较大的误差。这是因为在对复杂流体求解时，有限体积法的处理效果要优于有限元法。而有限体积法的理论精度仅为二阶，计算的精度不能确保符合实际需要。

分析油浸变压器的传热机理，主要有如下几个过程：铁心和绕组内部的金属热传导，绕组与铁心和油之间的导热过程，变压器油的对流传热，油与散热片之间的热传导，油箱壁与散热片对变压器周围的散热。铁心和绕组是变压器的主要发热体，而且其结构单一，没有流动现象，故采用精读较高的有限元法比有限体积法更为合适。在应对变压器油的对流传热，采用有限体积法更能发挥其善于处理较大规模流体运动传热问题的优点。

对于变压器绕组和铁心部分，使用网格质量较高的六面体网格。利用预条件共轭梯度法计算其金属导热规律，采用有限元方法计算时，绕组和铁心的计算精度选为四阶，保证了计算的精确性。同时由于绕组部分的体积远小于油的体积，也确保计算速度可以接受。

对于绕组铁心和变压器油之间的对流换热，变压器油的流动传热，和油与散热片之间的换热过程，采用有限体积法进行计算。

4.2 综合运用有限元法和有限体积法的仿真计算方法

文中以一台31 500 kVA/110 kV自然循环风冷（ONAF）变压器为例，计算得到了变压器内部的温度场分布。模型中变压器油、绕组和铁心的物理尺寸和参数均按照实际运行变压器的情况设计。

当外界温度为20℃时，给变压器按照额定负载情况加以发热情况的初值。利用上述的FEM与FVM结合的混合仿真方法，可以得到运行中的油浸式变压器内的温度场分布情况。利用混合方法计算得到的绕组温度的垂直方向分布结果如图1所示。

图1 变压器绕组温度随高度分布示意图Fig.1 Distribution schematic diagram of transformer winding temperature with height

图中横坐标表示绕组的纵向高度，纵坐标表示绕组纵向某点的温度值。从结果图中可以看出，绕组高度的约90%高度位置处的某点是绕组温度最高的热点，而最底部是温度最低点所在。这两者温度相差达15℃左右。低压绕组、中压绕组和高压绕组的热点温度依次为95℃左右、93℃左右、92℃左右。

其绕组的温度分布云图如图2所示。图3为油箱内部油的温度分布云图。由图3可以看出，处于油箱顶层的油温度最高，达77℃左右；油箱底层油温度最低，在52℃左右。

图2 运行中的绕组的温度云图Fig.2 Cloud image of transformer winding temperatures

图3 变压器油流的温度分布云图Fig.3 Distribution cloud image of transformer oil flow temperatures

驻马店铜山站1#主变是特变电工新疆变压器厂所产的31 500 kVA/110 kV自然油循环风冷变压器。为了验证计算结果，从现场收集了变压器顶层油温监测数据与变压器绕组热点温度，对监测数据与计算结果进行了对比。对比数据如表1所示，对比结果表明，利用有限元和有限体积法混合计算的方法得到的顶层油温和绕组热点温度，能够吻合实际的变压器温度监测数据。

由仿真数据和实际监测数据可知，油顶温度的仿真结果与实测温度误差在1.6℃以内，而绕组热点温度误差在3.2℃内，新的计算方法改善了对变压器温度场计算的精度。

表1 变压器实际运行数据和仿真数据对比Tab.1 Comparison of actual operation data and simulation data of transformer

5 结束语

（1）对有限体积法和有限元法的分析对比，由于有限元法和有限体积法不同的特点，因而在变压器温度场计算中，采用有限体积法计算流体温度场，有限元法来计算固体温度场的混合方法进行油浸式电力变压器的温度场计算；

（2）以一台31 500 kVA/110 kV自然循环风冷（ONAF）变压器为例，利用上述FEM和FVM混合方法计算得到了变压器内部的温度场分布。通过数据对比，所提方法可以准确地得到运行中变压器的温度数据，对变压器的运行和维护有一定的指导作用。