三剪应力统一强度理论研究
高江平 杨 华 蒋宇飞 吴鹏阁 孙世界
(长安大学特殊地区公路工程教育部重点实验室,西安 710064)
三剪应力统一强度理论研究
高江平1)杨 华 蒋宇飞 吴鹏阁 孙世界
(长安大学特殊地区公路工程教育部重点实验室,西安 710064)
材料强度理论研究是高等材料力学的一个重要研究领域,200多年来,各国学者提出了许多强度理论及试验研究结果.这些理论都是从不同的假设和力学模型出发,推导出不同的数学表达式,但一般只适用于某一类特定的材料.各种强度理论之间是否有联系?是否可能建立一个广泛适用的统一强度理论?自19世纪末以来,世界各国学者都在努力寻求建立统一强度理论,但一直没有成功.本文应用理论研究和试验验证相结合的方法,提出并验证了三剪应力统一强度理论。认为当作用于菱形十二面单元体上的三个主剪应力及其作用面上的三个正应力的函数达到某一极限值时,材料发生破坏.三剪应力统一强度理论是全应力理论,它用一个统一的线性表达式包含或逼近了现有的和其他新的各种单一和统一、线性和非线性、外凸和非凸的强度理论,形成了以单剪强度理论为下限、而以三剪应力强度理论为上限的一系列强度理论的新体系,实现了外凸强度理论和非凸强度理论的高度统一,使强度理论从适用于某一类材料、某种应力状态的单一强度理论发展为可以适用于各种材料及不同应力状态的统一强度理论,并能更大程度地发挥材料的强度潜力.通过与大量试验结果的对比分析表明:三剪应力统一强度理论可以广泛适用于各种材料及其不同的应力状态.
三剪应力统一强度理论,菱形十二面单元体,主剪应力,正应力,π 平面极限线,真三轴试验
引言
强度理论是高等材料力学的一个重要研究课题.200多年来,各国学者提出了众多的强度理论以及很多重要的试验结果.这些理论都从不同的假设和力学模型出发,推导出不同的数学表达式,一般只能适用于某一类特定的材料.各种强度理论之间有没有什么联系?有没有可能突破单一强度理论而建立一个广泛适用的统一强度理论?自19世纪末以来,世界各国学者都在努力寻求建立统一强度理论,但一直没有得到解决[1-7].
材料某点有三个主剪应力:最大主剪应力τ13、中间主剪应力τ12和最小主剪应力τ23.单剪强度理论仅考虑τ13对材料屈服破坏的影响.
俞茂襅教授同时考虑τ13和τ12对材料屈服破坏的影响,于1991年提出双剪统一强度理论的概念,并于1992年[8]和1994年[9]做了进一步的论述.双剪统一强度理论的提出开创了统一强度理论研究的新纪元,它是俞教授1961年双剪屈服准则[10-12]和1985年广义双剪应力强度理论[13]的发展,包括了从单剪强度理论到双剪强度理论的一族外凸极限面,达到了外凸强度理论的上限,实现了外凸强度理论的统一.
高江平同时考虑τ13,τ12和τ23对材料屈服破坏的影响,于2003年3月提出并于2003年4月完成三剪应力统一屈服准则[14],开辟了统一强度理论研究的新思路.后于2006年5月完成三剪应力统一强度理论体系[15],又于2010年和2015年进行了试验验证工作[16-17],并与其他文献的试验结果进行了对比分析,验证了三剪应力统一强度理论及其广泛适用性.三剪应力统一强度理论是一个新的强度理论体系,它实现了外凸强度理论和非凸强度理论的高度统一,并具有广泛的适用性,这是强度理论发展中的又一次进展.
1 三剪应力统一强度理论分析
1.1 三剪应力统一强度理论
1.1.1 主应力状态表达式
俞茂襅教授提出了正交八面单元体和菱形十二面单元体两种新型的材料单元体(如图1所示),他以正交八面单元体(如图1(a)所示)为依据,建立了双剪统一强度理论[18].

图1 材料的两种新型单元体Fig.1 Two kinds of new elements of materials
高江平以菱形十二面单元体(如图1(b)所示)为依据,建立了考虑菱形十二面单元体上全部应力分量的三剪应力统一强度理论[15].该理论认为:当作用于菱形十二面单元体上的三个主剪应力及其作用面上的三个正应力的函数达到某一极限值时,材料发生破坏.三剪应力统一强度理论的数学表达式为

式(1)也可写成如下形式

式中,τ13,τ12和τ23依次为最大、中间和最小主剪应力(当系数b和c不等于零的时候,三个主剪应力对材料的屈服破坏都有贡献,应同时考虑,双剪强度理论却没有考虑最小主剪应力的作用);σ13,σ12和σ23分别为各主剪应力作用面上的正应力;b为反映τ12和σ12综合作用对材料破坏强度影响的权系数(0≤b≤1);c为反映τ23和σ23综合作用对材料破坏强度影响的权系数(0≤c≤1);β为反映正应力对材料破坏强度的影响参数;f为材料的强度参数;f1,f2,f3分别为τ13与σ13,τ12与σ12及τ23与σ23综合作用的强度判据.

通过推导,可得出主应力形式的三剪应力统一强度理论表达式

材料参数β、f及权系数c由如下试验确定.
①单轴拉伸:σ1=σt,σ2=σ3=0;
②单轴压缩:σ1=σ2=0,σ3=−σc;
③双轴压缩:σ1=0,σ2=σ3=−σbc.
将试验结果代入式(4),可得三剪应力统一强度理论为[15]

其中,σt为材料的单轴拉伸强度;σc为材料的单轴压缩强度;σbc为材料的双轴压缩强度;α为材料的单轴拉压强度比;为材料的双轴与单轴压缩强度比.
双剪强度理论采用两个单元体,分别对应两个表达式,应用时首先根据τ12和τ23的大小判别应选用哪个单元体及其表达式.而本文的三剪应力统一强度理论采用同一个全应力单元体和同一个全应力表达式,这是一个广义的函数式,它涵盖了各种材料的各种应力状态及其π平面图形,即它们总是在以单剪强度理论为下限,而以三剪强度理论为上限的范围内变化.系数b与c取值都介于0与1之间,即使将公式(1)中τ12与τ23的位置互换,其结果都落在三剪应力统一强度理论π平面极限线范围之内,无论其结果是外凸或非凸的都可以,这正是三剪应力统一强度理论灵活之处.
1.1.2 极限线分析
(1)π平面上的极限线分析
由图2可知,主应力空间内一点与其在π0平面上投影点间有如下坐标映射关系

将式(6)代入式(5),即可得三剪应力统一强度理论在π0平面上的极限线方程[15]


图2 主应力空间与 π0 平面间的坐标映射关系Fig.2 The mapping relationships between the coordinates of the π0-plane and the principal stress
①若令式 (7)中b=c=0,则得


黏聚力c0和内摩擦角φ为Mohr-Coulomb单剪强度理论的抗剪强度参数.

图3 三剪应力统一强度理论 π0 平面极限线Fig.3 Limit loci of the three-shear stress unified strength theory in the π0-plane
②若令式 (7)中b=1,c=0,则可得直线的方程

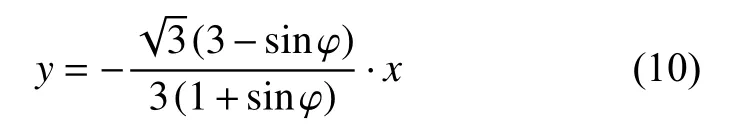
联立式(9)与式(10),解得b点的坐标

所求出的交点坐标x,y与俞茂襅双剪强度理论的极限线方程F与F′的交点的坐标完全相同[18].图3中,直线分别为双剪强度理论的极限线F和F′.
③若令式 (7)中b=c=1,则可得三剪应力强度理论极限线的方程



考虑π0平面上极限线关于y轴对称,由式(7)得

更一般地,求解式(12)与式(10)的方程组得二者的交点s2(xs,ys)的坐标

同理可得连接s与c两点的直线的方程为

式中

(2)三剪应力统一强度理论体系
与图3相似,根据坐标映射关系和极限线的三轴对称性及参数α,β,b,c的不同,可作出三剪应力统一强度理论π平面的系列极限线如图4(α≠1,β≠ 0)及图 5(α=1,β=0)所示.

图4 三剪应力统一强度理论 π 平面的系列极限线 (α ≠ 1,β ≠ 0)Fig.4 A series of limit loci of the three-shear stress unified strength theory(α≠1,β≠0)
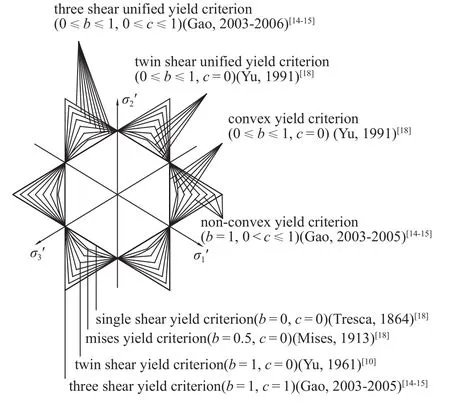
由三剪应力统一强度理论表达式(1)可得出外凸和非凸两大类强度理论(如图4所示)
①若令式 (1)中 0 ≤b≤1,c=0,则为一系列三剪外凸类强度理论
若b=c=0,则为 Mohr-Coulomb 单剪强度理论,为三剪应力统一强度理论的下限
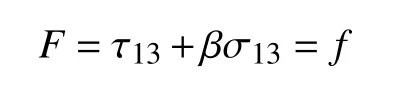
若 0 ≤b≤1,c=0,则为俞茂襅双剪统一强度理论[8]
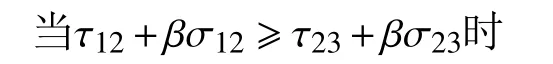

②若令式 (1)中b=1,0 若b=1,0 若b=1,c=1,则为三剪应力强度理论,即三剪应力统一强度理论的上限. 胡小荣等、郑颖人等和姚仰平等的强度理论[19-21]都属于外凸类非线性强度理论. 以上分析结果表明,三剪应力统一强度理论是全应力理论,它用一个统一的线性表达式包含或逼近了现有的和其他新的各种单一和统一、线性和非线性、外凸和非凸的强度理论,形成了以单剪强度理论为下限、而以三剪应力强度理论为上限的一系列强度理论的新体系,实现了外凸强度理论和非凸强度理论的高度统一,使强度理论从适用于某一类材料、某种应力状态的单一强度理论发展为可以适用于各种材料及其不同应力状态的统一强度理论,并能更大程度地发挥材料的强度潜力. 若令式(1)中β=0,可得出三剪应力统一屈服准则(如图5所示)[14] 图5 三剪应力统一屈服准则 π 平面的系列屈服线 (α=1,β=0)Fig.5 A series of yield loci of the three-shear stress unified criterion(α=1,β=0) 由式(15)可得出外凸和非凸两大类屈服准则. ①若 0 ≤b≤1,c=0,则为一系列三剪外凸类屈服准则. 若b=c=0,则为 Tresca 单剪应力屈服准则,即三剪应力统一屈服准则下限 若 0 ≤b≤1,c=0,则为俞茂襅双剪统一屈服准则[8] ②若b=1,0 若b=1,0 若b=1,c=1,则为三剪应力屈服准则,即三剪应力统一屈服准则的上限 三剪应力统一屈服准则包括以单剪应力屈服准则为下限、而以三剪应力屈服准则为上限的一系列屈服准则,现有的单剪屈服准则、双剪屈服准则、双剪统一屈服准则及其他屈服准则都是其特例或线性逼近,实现了外凸屈服准则和非凸屈服准则的高度统一,具有明确的物理意义,在理论上更加完善.这表明材料的屈服强度是随着材料的种类及其应力状态的变化而变化的,以往研究者从不同的角度研究得出的屈服准则,虽然表现形式不同,计算结果也存在差异,但都可视为适用于某类材料或某种应力状态时的屈服准则. (3)三剪应力统一强度理论主应力空间极限面 三剪应力统一强度理论在主应力空间的极限面的一般形式,是一系列以静水应力轴 (σ1=σ2=σ3)为轴线的不等边十二面锥面或由多边形线性逼近的曲面(图6为几种特例). 极限面的形状和大小与α,β,b,c值有关.当α=1,b=c=0 时,其极限面为无限长正六棱柱面. 由图6可见,三剪应力统一强度理论实现了从单剪强度理论、Mises强度理论、双剪强度理论到三剪应力强度理论及介于其间的一系列外凸类及非凸类强度理论的统一. (4)三剪应力统一强度理论平面应力状态的极限线 图6 三剪应力统一强度理论极限面 (α=1,β ≠ 0)Fig.6 The limiting surface of the three-shear stress unified strength theory(α=1,β ≠ 0) 三剪应力统一强度理论主应力空间极限面与σ1−σ2平面相交的截线即为该平面应力状态时的极限线,其形状随α,β,b,c值的大小而变化(如图 7 所示).当b=0,c=0 或b=1,c=0 时为六边形;当 0 在π平面上,三轴坐标σ1,σ2,σ3与直角坐标x,y,z的关系为 故方程(12)可表达为 图7 σ1−σ2 平面应力状态极限线Fig.7 The limit loci in plane stress state(σ1,σ2) 在π平面上,方程(17)的主应力形式为 在σ1−σ2平面应力状态的不同应力区,由方程(16)与方程(18)可推导出十二条极限线方程,由它们所构成的六角星形(最外边界的十二条直线所围成)如图7所示. 由图7可见,可由三剪应力统一强度理论得出平面应力状态下的一系列新的破坏准则和极限线. 在σ−τ复合应力状态下,三个主应力可表达为 将式(19)代入式(5),可得σ−τ复合应力状态的三剪应力统一强度理论表达式[15] 根据主应力与应力不变量之间关系 将式(21)代入式(5),可得三剪应力统一强度理论的应力不变量表达式[15] 式中,应力张量第一不变量 应力偏量第二不变量 高江平推导了三剪应力统一强度理论抗剪强度参数cs,φs的表达式[15] 式中,m为中间主应力系数 (0 m可以通过理论和实验来确定.在弹性区,m=2ν(v为材料的泊松比);在塑性区,m→1. 若令式 (23a)和式 (24)中b=c=0,则为 Mohr-Coulomb单剪强度理论参数c0,φ的表达式 若式 (23a)和式 (24)中b≠ 0,c=0,则得俞茂襅双剪统一强度理论参数ct,φt的表达式[18] 当m≠ 1 时 由三剪应力统一强度理论、双剪统一强度理论及单剪强度理论三者抗剪强度参数之间的关系,进一步论证了三剪应力统一强度理论使三者之间实现了完全统一. 单剪强度理论、双剪统一强度理论及三剪应力统一强度理论的特点如表1所示. 表1 三种强度理论的特点Table 1 The advantages of the three kinds of strength theory 试验土样为延安黄土,其重型标准击实试验的最大干密度为19.200 kN/m3,最佳含水率为12.20%,液限为30%,塑限为18.5%.制备的试件干密度为 17.640 kN/m3,饱和度为 65%.本次真三轴试验控制指标:含水率、密度、围压、b值.所拟定的重塑黄土真三轴试验方案如表2所示.试件的制备要通过配土样、闷料、压样和保湿等环节.试件尺寸为 70 mm×70 mm×70 mm,采用密度控制静压法分层压实制样.将试样移放至保湿缸中备用. 如图8,打开真三轴控制系统的操作界面,先三向施加30~50 kPa预压应力,待固结完成后进行试验.试验参数为:静应变速率0.07 mm/min,静应力速率10 kPa/min.设定试验结束条件是轴向应变达到15%,通过计算机进行控制. 绘制各试样等密度、等含水率、等固结围压、不同中主应力的重塑黄土真三轴试验应力应变曲线图,确定各曲线的屈服点,按各屈服点的p,q值绘出其在同一b值下的极限子午线,由极限子午线可知试样在同一p值下的屈服强度.根据b=0,0.25,0.5,0.75,1分别对应的罗德角,可以绘出各试样的π平面的屈服极限线(如图9所示). 表2 重塑黄土真三轴试验方案Table 2 The test plan of the true triaxial for remolding loess 图8 真三轴试验仪器Fig.8 The true triaxial experimental instrument 图9 重塑黄土真三轴试验结果Fig.9 Experimental results under true triaxial conditions for remolding loess 由图 9 可见:①围压σc=100 kPa 时,其屈服线与三剪应力统一强度理论的极限线 (b=0,c=0)较吻合,亦即与Mohr-Coulomb单剪强度理论相一致;②围压σc=200 kPa时,其屈服线与三剪应力统一强度理论的极限线 (b=0.5,c=0)较吻合;③围压σc=300 kPa时,绝大部分数据点与三剪应力统一强度理论的极限线 (b=1,c=0.5)较吻合. 以上分析表明:同一种材料(本例为重塑黄土)的屈服极限线是随应力状态而变化的,围压越大,屈服强度越高,而且均与三剪应力统一强度理论吻合较好. 通过与国内外已有文献试验结果的对比分析,进一步验证了三剪应力统一强度理论,并可广泛适用于各种材料. 金属类材料的试验结果[22]在单剪强度理论和三剪应力统一强度理论的极限线之间(如图10所示). 图10 金属材料的 π平面试验结果 (Taylor,Quinney,1931)[18]Fig.10 The experimental results in π-plane for metals(Taylor,Quinney,1931)[18] 火山岩真三轴试验结果[23]与三剪应力统一强度理论的极限线 (b=1/2,c=0)较吻合 (如图 11 所示). 图11 火山岩真三轴试验结果[23]Fig.11 The true triaxial experimental results for igneous rock[23] 花岗岩高压真三轴试验结果[24]与三剪应力统一强度理论的极限线 (b=1,c=1/8)相吻合,为非凸极限线(如图12所示). 混凝土真三轴试验结果[25]离散性比较大,但大多数试验点均落在三剪应力统一强度理论极限线的下限 (b=0,c=0)至上限 (b=1,c=1)之间 (如图13所示). 重塑淤泥的试验结果[26-27]与三剪应力统一强度理论的极限线 (b=1,c=1)较吻合,也为非凸极限线(如图14所示). 日本京都大学正常固结黏土试验结果与三剪应力统一强度理论的极限线 (b=1/2,c=0)较吻合(如图15所示). 英国砂土试验结果与三剪应力统一强度理论极限线 (b=1/2,c=0)较吻合 (如图 16 所示). 图12 花岗岩高压真三轴试验的π平面试验结果[24]Fig.12 The high pressure true triaxial experimental results in the π-plane for granite[24] 图13 混凝土真三轴试验的π平面试验结果[25]Fig.13 The experimental results in the π-plane for concretes[25] 图14 重塑淤泥真三轴试验的π平面试验结果[26]Fig.14 The true triaxial experimental results in the π-plane for remolding mud[26] 图15 正常固结黏土真三轴试验的 π 平面试验结果 (Shibata,Karube,1965)[18]Fig.15 The true triaxial experimental results in the π-plane for normally consolidated clay(Shibata,Karube,1965)[18] 图16 砂土的 π 平面试验结果 (Green,Bishop,1969)[18]Fig.16 The experimental results in the π-plane for sand(Green,Bishop,1969)[18] Ottawa细砂试验结果与三剪应力统一强度理论极限线 (b=1,c=0)较吻合 (如图 17 所示). 图17 Ottawa 细砂的 π 平面试验结果 (Dakoulas,Sun,1992)[18]Fig.17 The experimental results in the π-plane for the fine ottawa sand(Dakoulas,Sun,1992)[18] 由图9~图17可见,金属、岩石、混凝土、黏土、砂土和铸铁等多种材料的试验结果与三剪应力统一强度理论相符合,既有外凸屈服线,又有非凸屈服线,它们都介于单剪强度理论与三剪应力强度理论所包含的范围之内. 本文应用理论研究和试验验证相结合的方法,得到如下研究成果: (1)考虑菱形十二面单元体主剪面上所受到的三个主剪应力及其作用面上的三个正应力都对材料的屈服破坏产生影响,提出了三剪应力统一强度理论及其主应力表达式、应力不变量表达式、平面应力状态表达式和σ−τ复合应力状态表达式,形成了三剪应力统一强度理论体系. (2)绘制了三剪应力统一强度理论π平面极限线及其主应力空间极限面;进行了单剪强度理论、双剪统一强度理论及三剪应力统一强度理论的对比分析,并与许多试验结果进行了比较,结果表明三剪应力统一强度理论具有广泛的适用性. (3)三剪应力统一强度理论是全应力理论,它用一个统一的线性表达式包含或逼近了现有的和其他新的各种单一及统一、线性及非线性、外凸及非凸的强度理论,形成了以单剪强度理论为下限,而以三剪应力强度理论为上限的一系列强度理论的新体系,实现了外凸强度理论和非凸强度理论的高度统一,并能更大程度地发挥材料的强度潜力,使强度理论从适用于某一类材料、某种应力状态的单一强度理论发展为可以适用于各种材料及其不同应力状态的统一强度理论. 致谢感谢西安理工大学邵生俊教授对试验工作给予的大力支持! 1 Timoshenko SP.History of Strength of Materials.New York:Mc-Graw-Hill Book Co,1953 2 Rowlands RE.Strength(Failure)Theories and Their Experimental Correlation.Failure Mechanics of Composites Amsterdam:Elsevier,1985 3 Chen WF.Plasticity in Reinforced Concrete.New York:McGraw-Hill Book Company,1982 4 《中国大百科全书》(力学卷).北京:中国大百科全书出版社,1985:398(Encyclopedia of China(Mechanical Volume).Beijing:Encyclopedia of China Publishing House,1985:398(in Chinese)) 5 蒋彭年.土的本构关系.北京:科学出版社,1982(Jiang Pengnian.Soil Constitutive Relation.Beijing:Science Press,1982 (in Chinese)) 6 徐积善.强度理论及其应用.北京:水利电力出版社,1984(Xu Jishan.Strength Theory and Its Application.Beijing:Hydraulic Power Press,1984(in Chinese)) 7 俞茂襅.双剪应力强度理论研究.西安:西安交通大学出版社,1988(Yu Maohong.Researches on the Twin Shear Strength Theory.Xi’an:Xi’an Jiaotong University Press,1988(in Chinese)) 8 俞茂襅.强度理论新体系.西安:西安交通大学出版社,1992:82-84(Yu Maohong.New System of Strength Theory.Xi’an:Xi’an Jiaotong University Press,1992:82-84(in Chinese)) 9 俞茂襅.岩土类材料的统一强度理论及其应用.岩土工程学报,1994,16(2):1-10(Yu Maohong.Unified strength theory for geomaterials and its application.Chinese Journal of geotechnical Engneering,1994,16(2):1-10(in Chinese)) 10 俞茂襅.各向同性屈服函数的一般性质.西安交通大学科学技术报告,1961(Yu Maohong.General behaviour of isotropic yield function.Res.Report of Xi’an Jiaotong University,1961(in Chinese)) 11 Yu Maohong.Twin shear stress yield criterion.International Journal of Mechanical Sciences,1983,25(1):71-74 12 俞茂襅,何丽南.金属塑性变形的双剪应力准则.科学通报,1983,28(10):638-639(Yu Maohong,He Linan.Metal plastic deformation twin shear stress criterion.Chinese Science Bulletin,1983,28(10):638-639(in Chinese)) 13 俞茂襅,何丽南,宋凌宇.广义双剪应力强度理论及其推广.中国科学(A),1985,28(11):1113-1121(Yu Maohong,He Linan,Song Lingyu.Twin shear stress theory and its generalization.Science in China,Ser.A,1985,28(11):1113-1121(in Chinese)) 14 高江平,俞茂襅.三剪应力统一屈服准则研究.西安建筑科技大学学报(自然科学版),2005,37(4):526-530(Gao Jiangping,Yu Maohong.Study on the three shear stress unified yield criterion.Journal of Xi’an University of Architecture&Technology(Natural Science Edition),2005,37(4):526-530(in Chinese)) 15 高江平.力学的重要分支学科—土力学中的几个基本问题研究.[博士后出站报告].西安:西安交通大学,2006(Gao Jiangping.Study on the several basic problems of the soil mechanics-An important branch of the mechanics.[The Postdoctoral Outbound Report].Xi’an:Xi’an Jiaotong University,2006(in Chinese)) 16 杨华.三剪统一强度理论的理论分析及试验验证研究.[硕士论文].西安:长安大学,2010(Yang Hua.The study on theory analysis and experimental verification of the three shear stress unified strength.[Master Thesis].Xi’an:Chang’an University,2010(in Chinese)) 17 蒋宇飞.三剪应力统一强度理论对砂土的适用性研究.[硕士论文].西安:长安大学,2015(Jiang Yufei.Research the applicability of the three shear unified strength theory on sandy soil.[Master Thesis].Xi’an:Chang’an University,2015(in Chinese)) 18 俞茂襅.双剪理论及其应用.北京:科学出版社,1998(Yu Maohong.Twin shear theory and its application.Beijing:Science Press,1998(in Chinese)) 19 胡小荣,俞茂襅.材料三剪屈服准则研究.工程力学,2006,23(4):6-11(Hu Xiaorong,Yu Maohong.Resarchon triple-shear yield criterion for materials.Engineering Mechanics,2006,23(4):6-11(in Chinese)) 20 郑颖人,高红.材料强度理论的讨论.广西大学学报(自然科学版),2008,33(4):337-345(Zheng Yingren,Gao Hong.Discussion of strength theory for materials.Journal of Guangxi University(Nat Sci Ed),2008,33(4):337-345) 21 姚仰平,路德春,周安楠等.广义非线性强度理论及其变换应力空间.中国科学E辑,2004,34(11):1283-1299(Yao Yangping,Lu Dechun,Zhou An’nan,et al.Generalized non-linear strength theory and transformed stress space.Science in China(Series E),2004,34(11):1283-1299(in Chinese)) 22 Taylor GI,Quinney H.The plastic distortion of metal.Philosophical Transactions of the Royal Society A Mathematical Physical&Engineering Sciences,1931,230(5):323-362 23 Mogi K.Failure and flow of rocks under high triaxial compression.Journal of Geophysical Research Atmospheres,1971,76(5):1255-1269 24 李小春,许东俊.双剪应力强度理论的试验验证——拉西瓦花岗岩强度特性真三轴试验研究.中国科学院武汉岩土力学研究所,岩土(90)报告52号(Li Xiaocun,Xu Dongjun.Experimental verification of the twin shear strength theory-true triaxial test research of strength of the granite in a large power station at yellow river.Research Report(Rock and Soil 1990-52)of Institute of Rock and Soil Mechanics,Chinese Academy of Science(in Chinese)) 25 过镇海.混凝土的强度和本构关系—原理与应用.北京:中国建筑工业出版社,2004(Guo Zhenhai.The Strength and Constitutive Relation of Concrete.Theory and Application.Beijing:China Building Industry Press,2004(in Chinese)) 26 Haythornthwaite RM.Stress and Strain in Soils.In:Lee E H,et al.eds.Plasticity,Proc.2nd Symp.Naval Structural Mechanics.Oxford:Pergamon,1960:185-193 27 Haythornthwaite RM.Range of yield condition in ideal plasticity.Transactions of the American Society of Civil Engineers,1961,87(6):117-133 28 俞茂襅.强度理论新体系:理论、发展和应用(第二版).西安:西安交通大学出版社,2011(Yu Maohong.New System of System of Strength Theory,Development and Applications(Second Edition).Xi’an:Xi’an Jiaotong University Press,2011(in Chinese)) 29 Yu Maohong.Unified Strength Theory and Its Applications.Belin:Springer,2004 30 Yu MH,Ma GW,Qiang HF.Generalized Plasticity.Belin:Springer,2006 31 皱苹,钟鸣,龙志林等.Mohr-Coulomb屈服准则与Drucker-Prager屈服准则在块体非晶合金中的应用.中国有色金属学报,2015,25(5):1200-1208(Zhou Ping,Zhong Ming,Long Zhilin,et al.Applications of Mohr-Coulomb yield criterion and Drucker-Prager yield criterion in bulkamorphous alloys.The Chinese Journal of Nonferrous Metals,2015,25(5):1200-1208(in Chinese)) 32 潘家军,程展林,余挺等.不同中主应力条件下粗粒土应力变形特性试验研究.岩土工程学报,2016,38(11):2078-2084(Pan Jiajun,Cheng Zhanlin,Yu Ting,et al.Experimental study on stress-strain characteristics of coarse-grained soilunder different intermediate principal stresses.Chinese Journal of Geotechnical Engineering,2016,38(11):2078-2084(in Chinese)) 33 张常光,范文,赵均海.非饱和土统一强度理论及真三轴试验结果验证.岩石力学与工程学报,2015,34(8):1702-1711 (Zhang Changguang,Fan Wen,Zhao Junhai.Unified strength theory of unsaturated soils and Verification with true triaxial test.Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1702-1711(in Chinese)) 34 罗丹旎,李庆斌,胡昱等.基于统一强度理论的高强混凝土强度准则.水利学报,2015,46(1):74-82(Luo Danni,Li Qingbin,Hu Yu,et al.Strength criterion for high-strength concrete basedon the unified strength theory.Journal of Hydraulic Engineering,2015,46(1):74-82(in Chinese)) 35 邵生俊,陈菲,代亚锋等.结构性黄土的剪切带及强度特性的真三轴试验研究.岩土力学,2015,36(增刊1):66-70(Shao Shengjun,Chen Fei,Dai Yaifeng,et al.Shear band mechanism and strength characteristics of structural loesstested by true triaxial apparatus.Rock and Soil Mechanics,2015,36(Supplement1):66-70 (in Chinese)) 36 张哲峰,屈瑞涛,刘增乾.金属玻璃的断裂行为与强度理论研究进展.金属学报,2016,52(10):1171-1182(Zhang Zhefeng,Qu Ruitao,Liu Zengqian.Advances in fracture behavior andstrength theory ofmetallic glasses.Acta Metallurgica Sinica,2016,52(10):1171-1182(in Chinese)) 37 黄茂松,姚仰平,尹振宇等.土的基本特性及本构关系与强度理论.土木工程学报,2016,49(7):9-35(Huang Maosong,Yao Yangping,Yin Zhenyu,et al.An overview on elementary mechanical behaviors,constitutive modeling and failure criterion of soils.China Civil Engineering Journal,2016,49(7):9-35(in Chinese)) 38 苑宝军,邓荣贵,杨涛.岩土材料偏应力屈服张量角及应用分析.地下空间与工程学报,2016,12(增刊2):452-456(Yuan Baojun,Deng Ronggui,Yang Tao.Yielding tensor angle of deviatoric stress in geotechnical material and its application.Chinese Journal of Underground Space and Engineering,2016,12(Supplement2):452-456(in Chinese)) 39 王骑虎.岩土材料破坏准则基本特性分析.中国矿业,2015,24(12):142-146(Wang Qihu.Study on the basic characters of failure criterions of geotechnical material.China Mining Magazine,2015,24(12):142-146(in Chinese)) 40 杨凤,万邵华,刘军等.一种新的各向同性金属材料屈服函数.塑性工程学报,2015,22(6):108-113(Yang Feng,Wan Shaohua,Liu Jun,et al.A new yield function on isotropic metals.Journal of Plasticity Engineering,2015,22(6):108-113(in Chinese)) 41 王衍汇,倪万魁,袁志辉.原状黄土的联合强度理论探讨.合肥工业大学学报(自然科学版),2015,38(12):1688-1692(Wang Yanhui,Ni Wankui,Yuan Zhihui.Discussion on joint strength theory tact loof ines.Journal of Hefei University Of Technology,2015,38(12):1688-1692(in Chinese)) 42 李艳,赵均海,李楠等.基于统一强度理论的厚壁套管柱三轴抗拉强度.工程力学,2015,32(1):234-240(Li Yan,Zhao Junhai,Li Nan,et al.Tri-axial tension strength of thick-walled casingstrings based on unified strength theory.Engineering Mechanics,2015,32(1):234-240(in Chinese)) 43 呼志明.节理岩体各向异性及其强度特征分析.[硕士论文].北京:北京交通大学,2015(Hu Zhiming.Analysis of the anisotropism and strength characters of jointed rock mass.[Master Thesis].Beijing:Beijing Jiaotong University,2015(in Chinese)) 44 李艳宇.三参数双τ2强度理论及其应用.[硕士论文].沈阳:沈阳工业大学,2016(Li Yanyu.Three parameters of twinτ2strength theory and it’s application.[Master Thesis].Shenyang:Shenyang University of Technology,2016(in Chinese)) 45 仲大中.岩石类材料强度理论的历史演变.[硕士论文].南京:南京大学,2016(Zhong Dazhong.The historical evolution of rock-like materials’ strength theory.[Master Thesis].Nanjing:Nanjing University,2016(in Chinese)) 46 俞茂襅.工程强度理论.北京:高等教育出版社,1999(Yu Maohong.Engineering Strength Theory.Beijing:Higher Education Press,1999(in Chinese)) 47 Yao YP,Wang ND.Transformed stress method for generalizing soil constitutive models.ASCE Journal of Engineering Mechanics,2014,140(3):614-629 48 Yao YP,Hu J,Zhou AN,et al.Unified strength criterion for soils,gravels,rocks and concretes.Acta Geotechnica,2015,10(6):749-759 49 万征,姚仰平,孟达.复杂加载下混凝土的弹塑性本构模型.力学学报,2016,48(5):1159-1171(Wan Zheng,Yao Yangping,Meng Da.An elastoplastic constitutive model of concrete under complicated load.Chinese Journal of Theoretical and Applied Mechanics,2016,48(5):1159-1171(in Chinese)) 50 韩铁林,师俊平,陈蕴生等.轴、侧向同卸荷下砂岩力学特性影响的试验研究.力学学报,2016,48(4):936-943(Han Tielin,Shi Junping,Chen Yunsheng,et al.Experimental study on mechanics characteristics of sandstone under axial unloading and radial unloading path.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):936-943(in Chinese)) 51 孟令凯,周长东,郭坤鹏等.一类新的超弹性-循环塑性本构模型.力学学报,2016,48(3):660-674(Meng Lingkai,Zhou Changdong,Guo Kunpeng et al.A new formulation of constitutive model for hyperelastic-cyclic plasticity.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):660-674(in Chinese)) 52 王国盛,路德春,杜修力等.基于S准则发展的混凝土动态多轴强度准则.力学学报,2016,48(3):636-653(Wang Guosheng,Lu Dechun,Du Xiuli,et al.Dynamic multiaxial strength criterion for concrete developed based on the s criteiron.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):636-653(in Chinese)) STUDY OF THREE-SHEAR STRESS UNIFIED STRENGTH THEORY Gao Jiangping1)Yang Hua Jiang Yufei Wu Pengge Sun Shijie The strength theory is an important research subject in advanced mechanics.Many strength theories and important experimental results have been put forward by the scholars all over the world since 200 years ago.Different mathematical expressions were deduced based on different assumptions and mechanical models in these theories which can only be applied to some specific materials.What is the relationship among various strength theories? Can we propose a unified strength theory that adapted to more kinds of materials? Considerable effort has been devoted to this important problem by many scientists all over the world since the end of the 19th century,but it has not been solved.The threeshear stress unified strength theory has been put forward and verified by the method of combining the theoretical study with the experimental verification in this paper.It is considered that the material will failure when the function of the three principal shear stresses and their corresponding three normal stresses which acting on the main shear planes of the dodecahedron element reaches a magnitude.The three-shear stress unified strength theory is the whole force theory,it uses a unified linear expression to contain or approximate the existing and other newly various single and unified,linear and unlinear,convex and non-convex strength theory,it forms a new strength theory system which the inner boundary is the single-shear strength theory and its external boundary is the three-shear stress strength theory,it brings about the highly unity of the strength theory,it develops the unified strength theory which can suitable for different kinds of materials under various stress states from the single-shear strength which only suitable for some specific materials under specific stress states,and it can make full use of the potential strength of the materials.It is shown that the three-shear stress unified strength theory can be widely suitable for different kinds of materials under various stress states from the fact that a large number of experimental results of materials are in agreement with this theory. three-shear stress unified strength theory,dodecahedron element,principle shear stress,normal stress,yield loci in the π-plane,true triaxial test TB121 A 10.6052/0459-1879-17-081 2017–03–12 收稿,2017–09–11 录用,2017–09–11 网络版发表. 1)高江平,教授,主要研究方向:道路材料与结构及强度理论研究.E-mail:2227940211@qq.com 高江平,杨华,蒋宇飞,吴鹏阁,孙世界.三剪应力统一强度理论研究.力学学报,2017,49(6):1322-1334 Gao Jiangping,Yang Hua,Jiang Yufei,Wu Pengge,Sun Shijie.Study of three-shear stress unified strength theory.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1322-1334






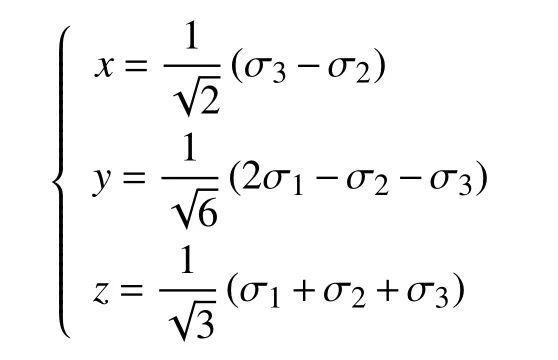



1.1.3 σ−τ复合应力状态的三剪应力统一强度理论


1.1.4 三剪应力统一强度理论的应力不变量表示

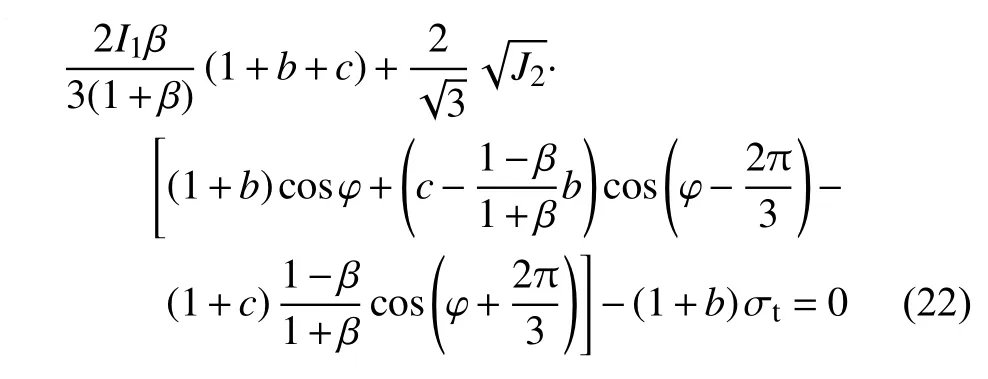


1.2 三剪应力统一强度理论的抗剪强度参数
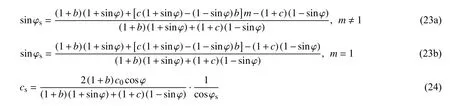

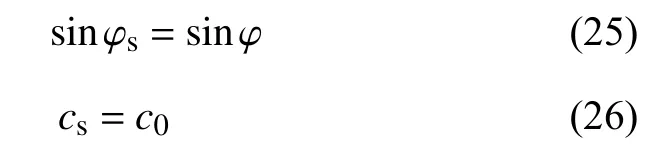

1.3 三种强度理论的比较

2 三剪应力统一强度理论的验证
2.1 重塑黄土的真三轴试验验证[16]
2.1.1 试验简介
2.1.2 试验数据整理及成果分析



2.2 其他材料的试验验证[16-52]
2.2.1 金属材料强度试验结果

2.2.2 岩石材料强度试验结果

2.2.3 混凝土材料强度试验结果
2.2.4 黏性土材料强度试验结果
2.2.5 砂性土材料强度试验结果






3 结论
(Key Laboratory for Special Area Highway Engineering Ministery of Education,Chang’an University,Xi’an710064,China)

