BP神经网络激励函数改进研究
张红玉,丁 宁,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
BP神经网络激励函数改进研究
张红玉,丁 宁,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
针对BP神经网络算法收敛速度慢、收敛精度低等缺陷,提出了一种改进的BP网络算法,即在S型传递函数(激励函数)中引入位移因子,给出了具体函数公式及改进算法.对不同位移因子所产生的运行结果进行比对,给出了位移因子合适的取值范围,将改进的函数集成到MATLAB神经网络工具箱中.最后,应用改进算法进行仿真,实验结果表明,相对于标准BP算法,改进算法的收敛速度提高了61%,收敛精度达到0.003 1,验证了改进函数的可行性,收敛速度和收敛精度均得到了改善.
BP神经网络;激励函数;Logistic曲线;位移因子
0 引 言
反向传播(Back-Propagation,BP)神经网络是一种多层前向神经网络,可实现从输入到输出的任意非线性映射,其权值的调整采用反向传播的人工神经网络.在标准BP神经网络算法中,神经元激励函数通常采用单、双极S型函数.然而,标准的Sigmoidal函数形式单一,其映射范围和位置都是固定不变的,缺少灵活性,这与神经网络的泛化能力不协调,无法改善神经网络的收敛速度慢、收敛精度低、易陷入局部极小解等问题[1-4].针对标准BP算法存在的缺陷,很多学者进行了研究并提出了改进方案,比如,文献[5]提出了一种含有4个待定参数的神经元激活函数,然而,在实际应用中,由于该方法所含参数较多,耗费了大量时间.本文在文献[5]研究的基础上,结合当下应用较多、较成熟的MATLAB神经网络工具箱中的传递函数,提出了一种高效可调带位移因子的激励函数,经过仿真实验验证,该函数能够满足BP算法快速收敛的需求.
1 BP模型传递函数的改进
1.1 理论知识


1.2 BP算法收敛速度影响因素分析


(1)

(2)
其中,η为算法的学习速率,E为误差函数,f′为神经元传递函数的导数,I为神经元节点的输入量,O为神经元节点实际输出量,y为神经元节点期望输出量.
由权值变化量公式可知,BP网络收敛速度由两部分决定,一是学习率η.学习率一般不宜过大,学习率太大将导致网络在训练过程中出现振荡或者发散现象,学习率太小将导致权值阈值更新速度慢,通常学习率设置为较小正数,本文选取学习率为0.05.另一个是传递函数的导数,当网络落到误差函数平坦区域时(如逐渐收敛到近零区域时),传递函数的导数比较小将导致网络权值和阈值φ更新速度减慢,从而耗费更多时间来训练网络,增加时间成本.
1.3 算法改进
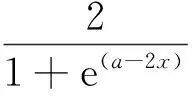
从改进后的传递函数导数可知,通过调整c的大小来改变传递函数导数的大小,从而控制收敛算法速度.BP算法的执行过程如下:
1)初始化权值w和阈值φ,系统随机赋值;
2)根据给定的输入I和期望输出y进行正向传播训练,计算实际输出O和误差E;
3)反向传播误差量,计算△w,修正权值;
4)若误差精度或者循环次数达到设定标准,输出结果,反之继续步骤2.
2 仿真实验测试
2.1 模型构建
本文将改进后的传递函数集成到MATLAB神经网络工具箱中,用该工具箱对改进后的算法进行仿真测试.首先,通过newff函数创建一个前馈神经网络对象,newff函数中有6个输入参数,新版MATLAB中第1个参数为输入元素的归一化矩阵,是一个R×2的矩阵,其中R表示输入元素的个数;第2个参数是每层神经网络的长度;第3个参数是一个包含各层神经元用到的传递函数的数组;第4个参数是训练网络所需的函数名称;第5个参数是权值和阈值的BP学习算法;第6参数是网络的性能函数.从理论上讲,所要求的任意函数都可以由三层BP神经网络来逼近,因此,本文采用三层神经网络结构进行仿真,改进算法后的神经网络结构如图1所示.

图1 三层神经网络模型示意图
网络初始参数设置如下:
net.trainParam.epochs=104∥设置训练迭代时间
net.trainParam.lr=0.05 ∥设置学习速度
net.trainParam.goal=10-6∥设置目标误差值
根据改进算法,连续改变位移因子a的值,得到了一组传递函数,并研究了这些函数对BP网络收敛速度的影响,计算结果如表1所示.

表1 位移因子改变对性能参数影响
由仿真结果可知,当a=0时,即传递函数为初始网络函数,迭代较慢;当a≤0时,迭代次数略微较少,但迭代速度依旧比较慢,并无明显提升;当a≥0时,随着其值的增大,迭代次数明显减少,表明收敛速度不断加快.通过以上分析,不难发现,选用合适的位移因子,可以提高BP算法的收敛速度,节约时间成本.经证实加入位移因子的改进算法具有实用性,可以推广使用.
由表1可以看出,当a值大于0时,收敛速度较快,但当a值过大,虽然速度有所提高,但收敛精度降低,因此,在实际选取时,位移因子不宜过大.综合收敛速度和收敛精度两方面因素,经过大量仿真实验证明a取小于18的正值,模拟效果较好,本文选取其中的一个值a=4进行仿真实验.
2.2 预测AQI指数
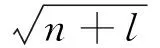

选取杭州市2015年11月至2016年1月共90个空气质量数据作为输入数据,所有数据输入训练系统后进行归一化处理,统一各输入量的数量级,避免了各输入量不同单位带来的影响,其中90%的数据用于训练网络,10%的数据用于预测结果,利用MATLAB建立改进后的BP神经网络,进行网络训练.网络进行训练后,得到输入层神经元与隐含层神经元之间的连接权值w12和阈值φ1,具体数值如下:
同时得到隐含层神经元与输出层神经元之间的连接权值和阈值分别为:
w23=(-0.623 6 0.973 0 0.106 4),φ2=-0.092 5.
在以上权值和阈值前提下,对标准BP算法和改进的BP算法进行模拟仿真和对比,结果如表2所示.

表2 仿真结果对比
以上测试结果表明,改进后的BP算法预测结果与给定的期望输出值很接近,经过78次迭代达到设定要求,而标准BP算法则需要迭代198次,改进算法迭代速度提高了60.61%,相比传统算法,提高了收敛速度,节约了时间成本.改进算法经过多次迭代训练学习,均方误差减小到0.003 1,可以看出,BP神经网络的收敛精度得到提高,说明本文提出的改进算法在收敛速度和精度上,都得到了较好的效果.
进一步进行仿真模拟,总样本数据为90个,其中90%用于训练,10%用于测试,改进算法的训练曲线和预测图及训练数据和样本数据的拟合情况如图2所示.

图2 改进后训练曲线和预测结果
改进算法的预测结果能很好地逼近所有样本点,实现了空气质量指标AQI与6种污染物之间的函数映射关系,改进后的BP算法练精度较高,能较好地实现预测.
训练数据与实际数据的相关性如图3所示.
相关度的计算公式为



图3 训练数据与实际数据的相关度
通过计算得到,训练数据与实际数据相关度为99.30%、确认数据与实际数据相关度为99.02%、测试数据与实际数据相关度为99.87%、总数据与实际数据相关度为99.30%.当数据相关度R>80.00%时,即可认为两个变量具有很强的相关性,或者观察拟合线与标准线重合程度,重合程度越好,表明拟合效果越接近.通过计算和图3可知,训练数据与实际数据拟合效果较好,精度较高.
3 结束语
本文针对标准BP算法中各神经元节点的激励函数模式固定的缺陷,在MATLAB工具箱中常用的神经元传递函数上增加了一个可调的位移因子,提出了一种带可调位移因子的激励函数形式,并通过实际案例验证了其有效性,为后续研究BP算法提供了一定的思路.但本文提出的改进算法也存在局限,本文改进的函数只针对S型函数,针对其他函数形式的研究有待进一步展开.
[1] Norio Baba. A new approach for finding the global minimum of error function of neural networks[J].Neural Network,1989,2(5):367-373.
[2] 向国全,董道珍.BP模型中的激励函数和改进的网络训练法[J].计算机研究与发展,1997,34(2):113-117.
[3] 陆金桂,王石刚,胡于进,等.多层神经网络算法的研究[J].计算机工程,1994,20(1):17-19.
[4] 徐宜桂,史铁林,杨叔子.BP网络的全局最优算法[J].计算机科学,1996,23(1):73-75.
[5] 李恩玉,杨平先,孙兴波.基于激活函数四参可调的BP神经网络改进算法[J].微电子学与计算机,2008,25(11):89-93.
[6] 石灵芝,邓启红,路婵,等.基于BP人工神经网络的大气颗粒物PM10质量浓度预测[J].中南大学学报(自然科学版),2012,43(5):1969-1974.
[7] 吉祝美.环境空气质量标准新标准解读[J].污染防治技术,2012,25(6):67-69.
ResearchontheImprovementofBPNeuralNetworkExcitationFunction
ZHANG Hongyu, DING Ning, XU Jiangrong
(InstituteofEnergy,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
In view of the shortcomings of the BP neural network algorithm, such as low convergence rate and low convergence precision. An improved BP network algorithm is proposed, in this method, the displacement factor is introduced into the S-type transfer function. And then, the concrete function formula and the improved algorithm are given. By comparing the results of different displacement factors, the appropriate range of the displacement factors is given. The improved functions are integrated into the MATLAB neural network toolbox and compared with the performance of the standard BP algorithm. Finally, the simulation results show that the convergence rate of the improved algorithm is 61% higher than that of the standard BP algorithm and the convergence rate is 0.0031, through real data simulation results demonstrate the improved algorithm is feasible, convergent and convergent.
BP neural network; excitation function; logistic curve; displacement factor
10.13954/j.cnki.hdu.2017.06.012
2016-12-12
国家自然科学基金资助项目(51176044);浙江省自然科学基金资助项目(Y1111085)
张红玉(1990-),女,黑龙江鸡西人,硕士研究生,能源机械.通信作者:丁宁副教授,E-mail:tinin@hdu.edu.cn.
O241
A
1001-9146(2017)06-0062-05

