一类线性离散网络控制系统的稳定性准则

唐超超，姜偕富，范化续，张译文

(杭州电子科技大学自动化学院，浙江 杭州 310018)

一类线性离散网络控制系统的稳定性准则

唐超超，姜偕富，范化续，张译文

(杭州电子科技大学自动化学院，浙江 杭州 310018)

研究了一类线性离散网络控制系统的稳定性问题.通过引入增广矩阵，改进现有一些研究的Lyapunov-Krasovskii泛函；同时为了利用更多的时滞信息，引入了三重求和项.采用离散形式的Wirtinger不等式方法和凸组合方法，通过LMIs形式给出了一类线性离散网络控制系统稳定性准则.最后，通过数值示例验证了所采用方法的有效性.

网络控制系统；Lyapunov-Krasovskii泛函；增广矩阵；LMIs；稳定性准则

0 引言

网络控制系统(Netwoked Control Systems,NCSs)是控制理论和计算机网络通讯技术相结合的产物，因其较好的应用前景，受到了国内外相关领域学者的广泛关注[1-3].网络带宽限制引起的数据传输时滞往往使系统性能变差甚至不稳定，近年来，随着对网络控制系统稳定性的深入研究，使其研究成果得到不断丰富.文献[2]通过引用自由权矩阵方法获得保守性较小的稳定性准则，但是用此方法，增加了计算处理的复杂度.文献[3]在处理差分求和项时，采用Jensen不等式方法给出了一种改进的Lyapunov-Krasovskii稳定性准则.文献[4-5]采用离散形式的Wirtinger不等式方法来处理差分求和项，获得了比文献[3]具有较小保守性的稳定性准则，但是文献[5]构造的Lyapunov-Krasovskii泛函依旧采用以前的泛函构造形式.近年来相比较连续系统，相关学者对于离散系统的研究成果不是那么丰富，而实际系统中对于离散系统的研究也很有必要.因此，对于线性离散网络控制系统稳定性结果的保守性的研究仍有很大的改进空间.为此，本文对线性离散网络控制系统的稳定性进行了研究，获得保守性较小的稳定性准则.首先，基于文献[4]，对现有一些研究的Lyapunov-Krasovskii泛函进行适当的改进，使其包含更多的时滞信息；其次，在对Lyapunov-Krasovskii泛函的差分处理过程中，添加合适的自由矩阵并利用凸组合方法避免了对交叉项不等式约束进行界定；最后，采用的最新提出的离散形式Wirtinger不等式方法获得了保守性更小的稳定性准则.

1 系统描述

本文中，研究如下基于网络控制的离散系统：

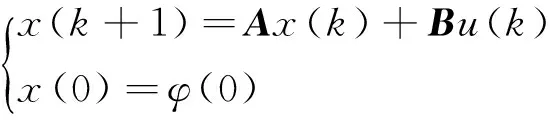
(1)

式中，x(k)∈Rn是状态向量；φ(0)是初始状态；u(k)∈Rp是输入向量；A，B是分别具有适当维数常矩阵.考虑网络控制系统的状态反馈控制器为：

u(k)=Kx(tk)

(2)

式中，K是给定的状态反馈控制器增益，tk表示传感器第k个采样时刻.

假设d(k)=k-tk，基于式(1)和(2)则闭环系统可以表示为：

x(k+1)=Ax(k)+BKx(k-d(k))

(3)

式中，d(k)是闭环系统(3)的时变时滞，为一个非负整数，假设d(k)满足0≤d1≤d(k)≤d2，d1和d2为非负整数且分别为时滞d(k)的下界和上界.

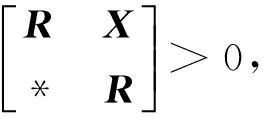
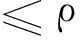
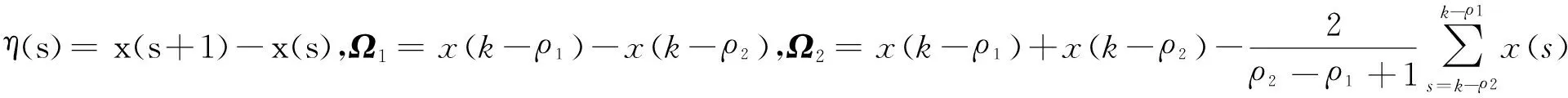
引理3[7]给定矩阵Q=QT，具有适当维数的矩阵H和E，则Q+HFE+ETFTHT<0对于所有满足FTF≤I的矩阵F成立，当且仅当存在标量λ>0，使得Q+λHHT+λ-1ETE<0成立.

2 主要结果

2.1 标称离散网络控制系统稳定性准则

针对标称离散网络控制系统(3),给出如下稳定性准则.

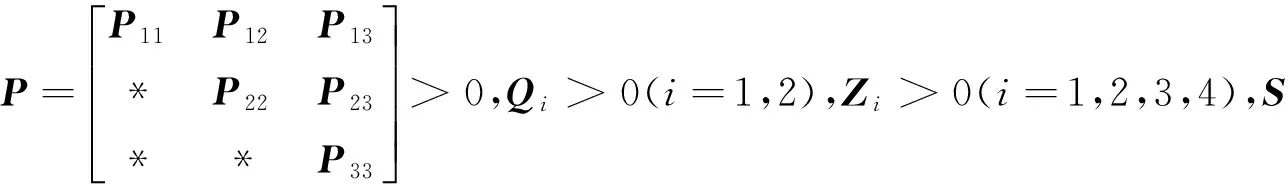
(4)

(5)

其中：

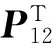
Ξ12=-2Z1-(A-I)TP12-P23-P12+P13,

Ξ13=(A-I)TP11BK+P11BK-(A-I)TP13-P23+(A-I)TΨBK+Z3-S,

Ξ14=-P13-(A-I)TP13+S,

Ξ15=6Z1+(1+d1)P22+(1+d1)(A-I)TP12+(1+d1)2Z4,

Ξ16=(d(k)-d1+1)(A-I)TP13+(d(k)-d1+1)P23,

Ξ17=(d2-d(k)+1)(A-I)TP13+(d2-d(k)+1)P23,

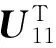
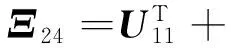
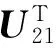
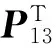
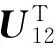
Ξ36=2U12+2U22+6Z2+(d(k)-d1+1)KTBTP13,

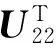
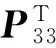
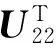
证明构造如下Lyapunov-Krasovskii泛函

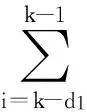
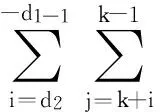
(6)

选取的增广矩阵如下：

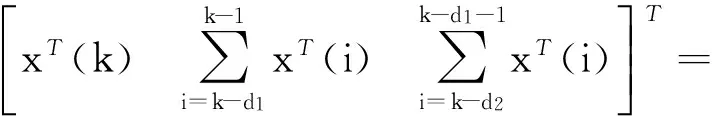
(Π2+Π(d(k)))ξ(k),

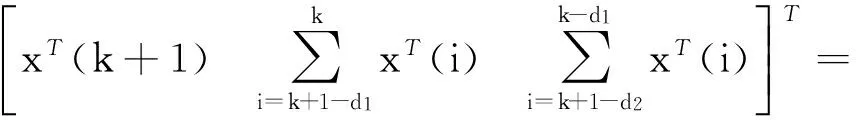
(Π1+Π(d(k))ξ(k),

其中：

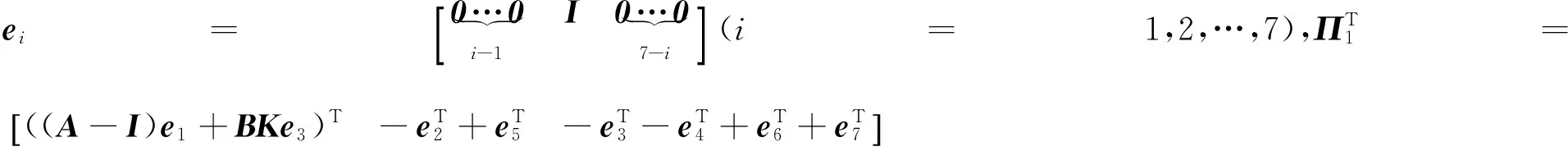
对Lyapunov-Krasovskii泛函进行差分计算：

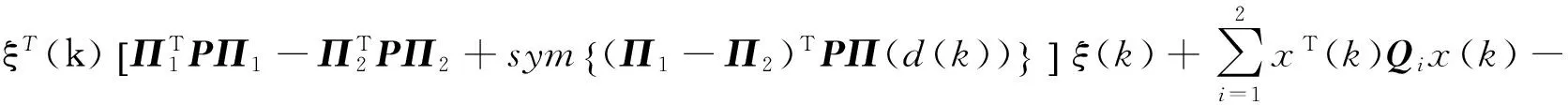
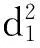
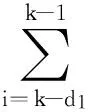
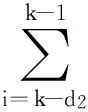
(7)

对式(7)中部分差分求和项做如下处理，由引理2中的离散形式的Wirtinger不等式方法可得：

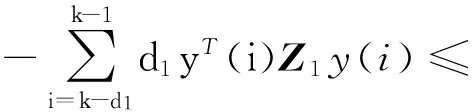
(8)

采用文献[5]中的方法并根据引理1,对于任意的矩阵U满足式(4)则有

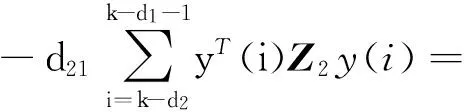
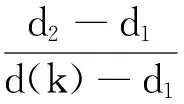
(9)

其中：

Φ1=-(e1-e2)TZ1(e1-e2)-3(e1+e2-2e5)TZ1(e1+e2-2e5),

Φ2=-(e2-e3)TZ2(e2-e3)-3(e2+e3-2e6)TZ2(e2+e3-2e6),

Φ3=-(e3-e4)TZ2(e3-e4)-3(e3+e4-2e7)TZ2(e3+e4-2e7),

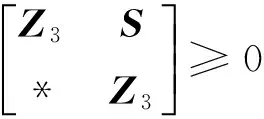
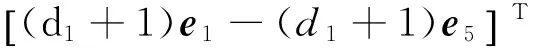
(10)

结合式(7)-(10)，可得ΔV<ξT(k)Ξξ(k).由式(5)知，当Ξ|d(k)=d1<0和Ξ|d(k)=d2<0同时成立时，则线性离散网络控制系统(3)是渐近稳定的，证毕.

2.2 参数不确定系统的鲁棒稳定性准则

实际系统中，由于存在元件老化等一些不确定因素，所以，本文进一步研究一类线性离散网络控制系统的鲁棒稳定性准则，研究如下基于网络控制的参数不确定线性离散系统：

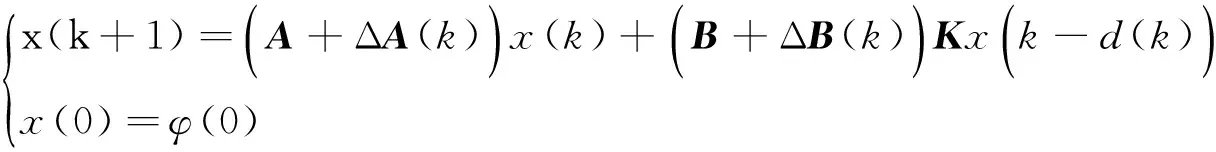
(11)

式中，ΔA(k)，ΔB(k)是具有适当维数的不确定时变矩阵并假设具有如下形式

[ΔA(k),ΔB(k)]=HF(k)[E,Eb]

式中，H，E，Eb为已知的常数矩阵，F(k)为不确定函数矩阵，并假设F(k)满足如下式子：

FT(k)F(k)≤I

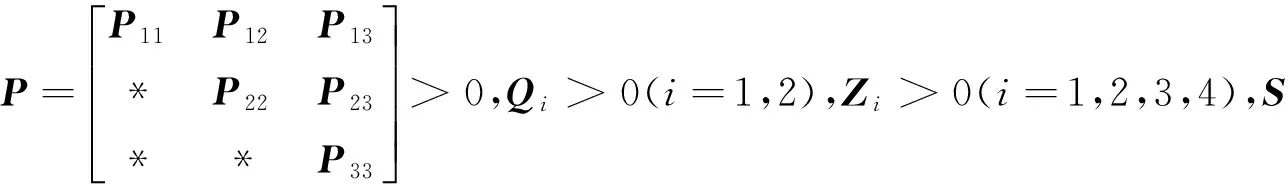
(12)

其中：

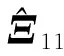
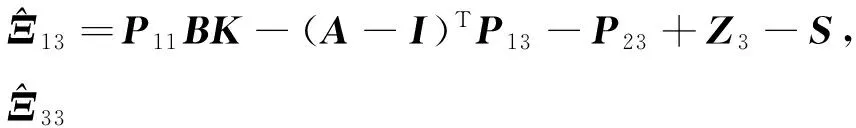
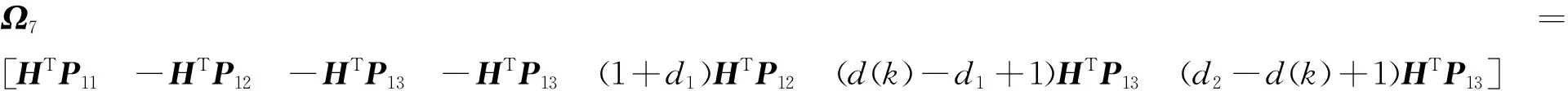
证明由Schur补引理，定理1中的Ξ转变为

(13)

其中：

η=[E0EbK000000000]

θ=[HTP11-HTP12-HTP13-HTP13(1+d1)HTP12(d(k)-d1+1)HTP13

(d2-d(d)+1)HTP13HTHTHTHTHT]

当λ>0时，由引理3可以得到：

(14)

应用Schur补引理，式(14)等价于式(12).证毕.

3 数例

例1本文考虑式(3)对应的参数[3,4,6]：

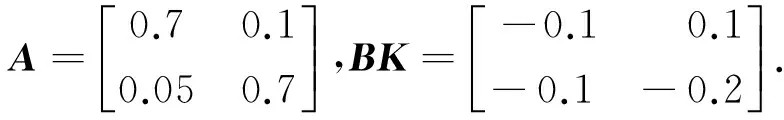
由本文给定的稳定性准则,利用MATLAB中的LMI工具箱分别改变时滞下限d1值，求得系统的最大允许时滞上界d2，与相关文献比较结果如表1所示.

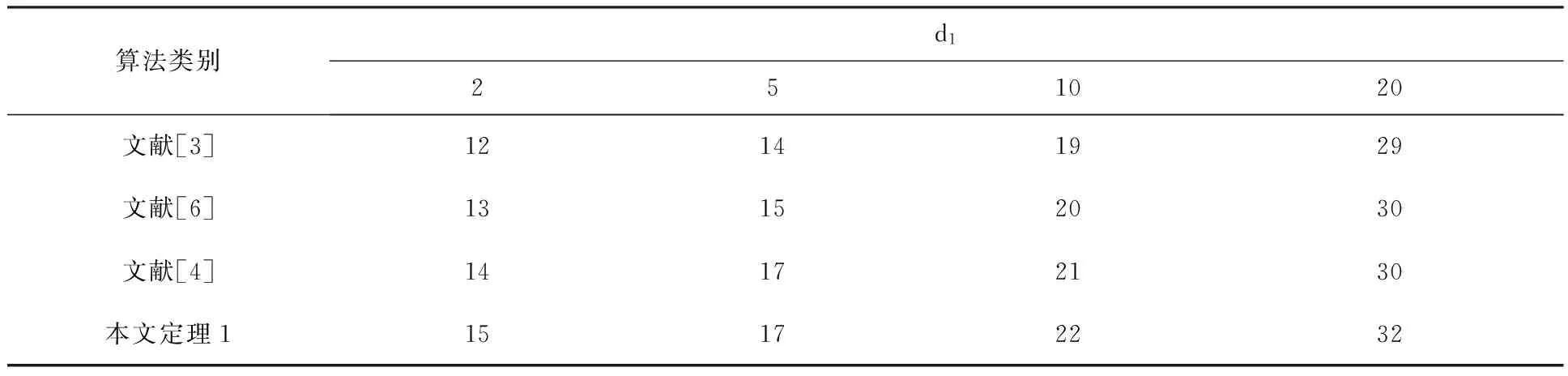
表1 不同d1值下，最大允许时滞上界d2的比较

文献[3]采用Jensen不等式处理差分求和项，文献[4]和文献[6]虽然引入了增广矩阵，但是没有充分利用时滞信息.本文采用了离散形式的Wirtinger不等式方法，并在构造泛函时引入增广矩阵.由表1可知，本文采用方法得到的稳定性准则的保守性更小.

例2本文考虑式(11)对应的参数[8,9]：

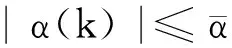
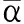
表2 不同时滞范围情况下的的上界

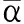
4 结束语

本文研究了线性离散网络控制系统的稳定性问题.针对原有一些文献研究存在的不足，采用增广矩阵和离散形式的Wirtinger不等式方法与采用自由权矩阵法相比，简化了计算复杂度，得到了保守性更小的一类线性离散网络控制系统稳定性准则.实际系统往往受到外部因素的干扰，因此，将要进一步研究外部扰动对系统的影响程度并设计一个控制器来抑制外部干扰对系统的影响.

[1] 刘建华,黄凌云.离散时滞网络控制系统的镇定和研究[J].中国海洋大学学报,2014,44(6):114-118.

[2] Chen P, Tian Y C. Robust H∞ Control of Networked Control Systems with Parameter Uncertainty and State-delay[J]. European Journal of Control,2006,12(5):471-480.

[3] Kwon O M, Park M J, Park J H, et al. Improved robust stability criteria for uncertain discrete-time systems with interval time-varying delays via new zero equalities[J]. IET Control Theory and Applications,2012,6(16):2567-2575.

[4] Nam P T, Pathirana P N, Trinh H. Discrete Wirtinger-based inequality and its application[J]. Journal of the Franklin Institute,2015,352(5):1893-1905.

[5] Kang W, Zhong S M, Shi K B, et al. Finite-time stability for discrete-time system with time-varying delay and nonlinear perturbations[J]. ISA Transactions,2016,60:67-73.

[6] Seuret A, Gouaisbaut F, Fridman E. Stability of discrete-time systems with time-varying delays via a novel summation inequality[J]. IEEE Transactions on Automatic Control,2015,60(10):2740-2745.

[7] Duan W Y, Cai C X,Liu Z F. Improved robust stability criteria for uncertain discrete-time lur’e systems with interval time-delay[J]. 2014 26th Chinese Control and Decision Conference (CCDC),2014:3178-3183.

[8] Ramakrishnan K, Ray G. Robust stability criteria for a class of uncertain discrete-time systems with time-varying delay[J]. Applied Mathematical Modelling,2013,37(3):1468-1479.

[9] Kwon O M, Park M J, Park J H, et al. Improved robust stability criteria for uncertain discrete-time systems with interval time-varying delays via new zero equalities[J]. IET Control Theory & Applications,2012,6(16):2567-2575.

StabilityCriteriaforaClassofLinearDiscrete-timeNetworkedControlSystems

TANG Chaochao, JIANG Xiefu, FAN Huaxu, ZHANG Yiwen

(SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

In this paper, the stability problems for a class of linear discrete-time networked control systems are studied. An augmented matrix is introduced to improve the Lyapunov-Krasovskii functional of some existing literatures; at the same time, in order to make use of more time-delay information, the triple summation term is introduced. By using the discrete Wirtinger-based inequality and the reciprocally convex approach, the stability criteria for a class of linear discrete-time networked control systems are given in the form of LMIs. Finally, numerical examples are given to demonstrate the effectiveness of the methods used in this paper.

networked control systems; Lyapunov-Krasovskii functional; augmented matrix; LMIs; stability criteria

10.13954/j.cnki.hdu.2017.06.009

2017-01-09

国家自然科学基金资助项目(61673148)；浙江省自然科学基金资助项目(LZ13F030001)

唐超超(1992-)，男，浙江衢州人，硕士研究生，控制科学与工程.通信作者：姜偕富教授，E-mail:jiangxf@hdu.edu.cn.

TP273

A

1001-9146(2017)06-0041-07