基于稀疏先验和边缘约束的图像盲去模糊算法
鲍宗袍,陈华华
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
基于稀疏先验和边缘约束的图像盲去模糊算法
鲍宗袍,陈华华
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
针对运动图像盲去模糊问题,提出了一种基于稀疏先验和边缘约束的运动图像盲去模糊算法.首先利用非维度高斯测度正则约束恢复中间清晰图像,然后借助T-smooth技术提取显著性边缘,并采用变分狄利克雷模糊核估计方法求得较为准确的模糊核.在非盲去模糊阶段,结合全变分与超拉普拉斯正则化方法的优缺点,将两种方法复原的图像取平均,减轻了复原图像中的振铃效应,同时保留了更多的图像细节.实验结果验证了提出的新算法的有效性,与其他算法相比,所提算法可以获得更准确的模糊核和较佳清晰图像.
盲去模糊;显著性边缘;非维度高斯测度;变分狄利克雷
0 引 言
在图像采集过程中,往往成像设备与拍摄场景之间存在一定的相对运动,导致图像变得模糊不清.针对运动图像盲去模糊问题,文献[1]首次提出一种极具影响力的非参模糊核估计方法;文献[2]提出一种非自然图像先验,在其盲去模糊模型中以l1/l2-范数约束图像梯度稀疏性,以l1-范数约束模糊核稀疏性取得了较好的效果;文献[3]提出一种迭代过程中逐步逼近l0-范数的MAP型盲去模糊算法.然而,基于图像梯度稀疏先验[1-3]的图像盲复原算法恢复出的图像往往存在比较严重的重影和噪声,其梯度信息会误导模糊核估计的迭代方向,导致最终复原得到的清晰图像包含较多的重影.为此,本文提出一种基于图像梯度非维度高斯测度(Nondimensional Gaussianity Measure,NGM)稀疏先验和边缘约束的运动图像盲去模糊算法,从估计得到的图像中提取有效的图像边缘,并以此指导模糊核的估计.鉴于模糊核的归一化先验以及模糊核的非负特性,本文利用文献[4]的狄利克雷分布逼近模糊核的后验分布,使得模糊核的解空间满足非负性质以及归一化性质,同时使得求解得到的模糊具有一定的稀疏性.
1 联合稀疏约束与边缘约束盲去模糊模型
1.1 非维度高斯测度
非维度高斯测度定义[4]如下:
(1)
其中,|x(i)|为向量x中第i个元素的绝对值;E[·]表示取平均操作.
RNGM(x)具有如下性质:当且仅当|x|=E[|x|]时,RNGM(x)取最大值;当且仅当x中只有一个元素|x(i0)|非零,RNGM(x)取最小值N/(N+1);这里N是向量x的维数.因此,减小RNGM(x)意味着将梯度|x|从其均值分离并且促使最终的|x|变得稀疏.清晰图像梯度|x|将会使得RNGM(x)具有较小的值,模糊图像梯度|y|使得RNGM(x)具有较大的值,这表明以非维度高斯测度作为先验有助于获得清晰图像.综上所述,使用非维度高斯测度作为待估图像的正则项,清晰图像估计模型为:
(2)
其中,H为由模糊核h组成的卷积矩阵;1,2分别为水平梯度算子和垂直梯度算子;λx为大于0的正则参数;λx控制着中间清晰图像梯度的稀疏性.
1.2 T-smooth技术提取图像强边缘
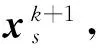
(3)
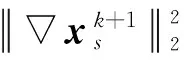
1.3 变分狄利克雷逼近模糊核后验分布
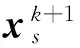
(4)
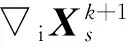
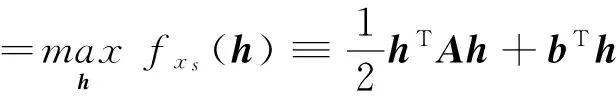
(5)
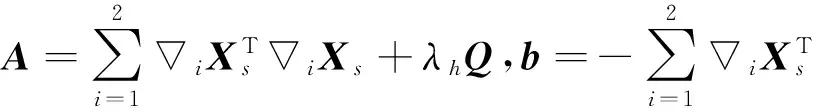
(6)
(7)
2 模型求解
2.1 增广拉格朗日求解中间清晰图像
为了减轻中间图像中的振铃效应,采用文献[8]中的不确定性边界条件.假设H=MpTh,Mp∈RM×N,N为图像像素个数,其作用是截取图像与模糊核卷积之后图像的有效区域;Th表示由模糊核h组成的卷积矩阵.令u=Thx和vi=ix,(i=1,2).运用增广拉格朗日法和乘子法将式(2)转换为:
(8)
其中,λu和λv为惩罚权重,d是拉格朗日乘子,利用交替迭代策略求解式(8)的优化问题.
u-子问题的求解:给定x,d和v,优化变量u等价于求解下面的优化问题:
(9)
显然,该问题是一个二次函数最小优化问题,对其求导并令导数等于0得到如下等式:
(10)
其中,I为单位矩阵.
拉格朗日乘子可以通过以下公式更新:
(11)
(12)
假设梯度算子满足周期边界条件,则上述x可以通过二维快速傅里叶变换(2D-FFT)在频域求得.
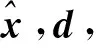
(13)
其中i=1,2;本文以前一次迭代求解得到的vi的均值E代替分母中的E[|vi|]近似求解:
(14)
其中λ=λx/λv,E=E[|vi|];w表示ix中的某一个元素.则z的迭代表达式为:
zt+1=sign(w)max(|w|-λE/(|zt|+E)2,0)
(15)
2.2 反向跟踪梯度投影算法求解模糊核
由文献[4]负熵项Eqα[logqα(h)]可以写成:
(16)
其中,ψ=Γ′/Γ称为digamma函数;1表示元素全为1的向量.结合狄利克雷概率密度函数、期望和协方差矩阵,则式(7)中的损失函数表达式如下:
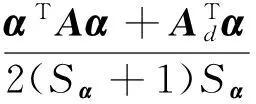
(17)
其中,Ad是矩阵A中的对角元素组成的向量,即Ad(i)=Aii,i=1,2,…K.采用反向跟踪梯度投影算法求解L(α)最小化问题.
3 非盲去模糊
模糊核h获得后需要采用非盲去模糊算法恢复最终的清晰图像.本文结合上述两种算法,采用优势互补策略[9],分别使用上述两种先验估计两幅清晰图像L1,L2,然后取两者平均得到最终的清晰图像.L1可由最小化超拉普拉斯先验约束的能量泛函获得
(18)
其中,0.5≤α≤0.8,ρ为权重.本文算法实现时α取0.8.L2可以通过下式获得:
(19)
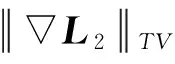
4 实验结果与分析
为了检验本文盲去模糊算法的有效性,本文分别在文献[6]的Levin测试集和实际拍摄的模糊图像进行仿真测试,并同现有算法进行比较.实验中,本文算法的主要参数设置如下:λx=1.5E-4,λu=0.1,λv=0.001,γ=1E-6,λh=0.01,T-smooth技术提取显著性结构涉及的参数参照文献[5]进行设置.对比的盲去模糊方法的参数按照原作者论文设置,计算盲反卷积误差累计直方图时采用与文献[6]相同的非盲去模糊方法,其余实验所有方法采用的非盲去模糊算法均采用本文非盲去模糊方法.Levin测试集包含32张模糊图像,由4张清晰图像分别与8个尺寸范围从13×13到27×27的大小不同的模糊核卷积生成的.图1给出了这4幅清晰图像和8个真实的模糊核.Levin数据集内每张清晰图像都具有8种不同模糊图像,表1列出了本文算法与其他算法在测试图像1至4的8张模糊图像上获得的清晰图像的平均PSNR值以及总体的PSNR值.由表1可知,本文方法获取的清晰图像具有较高的PSNR.
图2给出了Levin测试图像的盲去模糊误差比值[6](Ratio of Deconvolution Error, RDE)的累积直方图.RDE值越小则盲反卷积的效果越好.当盲去模糊误差比值RDE小于3时,此次盲去模糊成功.由图2可知,本文方法的Error Ratio-Success Rate曲线基本上落在其他曲线上方,在所有对比算法中本文算法具有一定的优势.

图1 4幅清晰图像与8个不同的模糊核
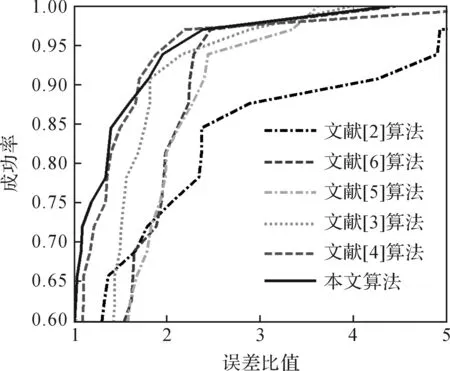
图2 Levin数据集上的盲反卷误差累计直方图

dB
图3针对测试图像-02和模糊核-07生成的模糊图像,给出了各算法得到的清晰图像及模糊核,同时计算了PSNR.从左到右从上到下依次为模糊图像,已知真实模糊核下使用本文非盲去模糊算法得到的清晰图像,文献[1,2,3,4,6,7]以及本文方法.在模糊核上文献[1]的方法和文献[2]的方法得到的模糊核连通性较差,文献[7]估计的模糊核虽然具有一定的连通性但其模糊核中出现了拖尾,文献[3]获得模糊核在连通性上不如本文且含少许噪点,文献[6]估计的模糊核存在许多孤立噪点.文献[4]获得复原图像在视觉上与本文方法最为接近.但是,本文方法获得的清晰图像的PSNR为30.80 dB,具有最高PSNR.
为了进一步验证本文算法的有效性,采用实际彩色模糊图像作为实验数据,并与文献[2,3,4,7,10,11,12]方法进行比较.获得模糊核后,将使用本文非盲去模糊方法反卷积得到最终的清晰图像.图4列出了模糊图像及各种算法获得的模糊核和清晰图像.由图4可知,本文方法估计的模糊核具有更精确的支撑和更少的噪声,获得的清晰图像具有更清晰的细节、更为锐化的边缘和较优的视觉效果.除文献[12]的方法外,图像的模糊核大小设置为55×55.实验结果表明除文献[3]的方法以及本文方法外其他方法均不能很好的获得模糊核,导致获得清晰图像视觉质量较差.因此,本文算法提高了模糊核的估计精度,提高了复原图像的质量.

图3 各个方法估计的清晰图像和模糊核

图4 实际彩色模糊图像及各种方法估计的清晰图像和模糊核
5 结束语
本文结合图像梯度稀疏先验和边缘约束,提出了一种新的运动图像盲去模糊算法.相比于其他算法,本文算法获得的模糊核具有更准确的支撑和较少的噪点,获得的清晰图像具有较优的视觉效果.本文盲去模糊模型所含参数较多,调整算法参数比较困难,后期工作将通过数据驱动的方式为模型自动学习正则化参数,进一步提高模糊核估计精度.
[1] Fergus R, Singh B, Hertzmann A, et al. Removing camera shake from a single photograph[J]. Acm Transactions on Graphics,2006,25(3):787-794.
[2] Krishnan D, Tay T, Fergus R. Blind deconvolution using a normalized sparsity measure[C]//Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE,2011:233-240.
[3] Xu L, Zheng S, Jia J. Unnatural l0 sparse representation for natural image deblurring[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2013:1107-1114.
[4] Zhou X, Mateos J, Zhou F, et al. Variational Dirichlet Blur Kernel Estimation[J]. Image Processing A Publication of the IEEE Signal Processing Society, IEEE Transactions on,2015,24(12):5127-5139.
[5] Xu L, Yan Q, Xia Y, et al. Structure extraction from texture via relative total variation[J]. Acm Transactions on Graphics,2012,31(6):439-445.
[6] Levin A, Weiss Y, Durand F, et al. Efficient marginal likelihood optimization in blind deconvolution[C]// Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE,2011:2657-2664.
[7] Cho S, Lee S. Fast motion deblurring[J]. Acm Transactions on Graphics,2009,28(5):89-97.
[8] Reeves SJ. Fast image restoration without boundary artifacts[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2005,14(10):1448-1453.
[9] Zhang X, Wang R, Tian Y, et al. Image deblurring using robust sparsity priors[C]//Image Processing (ICIP), 2015 IEEE International Conference on. IEEE,2015:138-142.
[10] Kotera J,roubek F, Milanfar P. Blind deconvolution using alternating maximum a posteriori estimation with heavy-tailed priors[C]//International Conference on Computer Analysis of Images and Patterns. Springer Berlin Heidelberg,2013:59-66.
[11] Zuo W, Ren D, Gu S, et al. Discriminative learning of iteration-wise priors for blind deconvolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,2015:3232-3240.
[12] Cai JF, Ji H, Liu C, et al. Framelet-based blind motion deblurring from a single image[J]. Image Processing A Publication of the IEEE Signal Processing Society, IEEE Transactions on,2012,21(2):562-572.
BlindMotionDeblurringBasedonSparsePriorandEdgeConstraints
BAO Zongpao, CHEN Huahua
(SchoolofCommunicationEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Concerning the removal problem of motion blur from a single photograph, a novel blind motion deblurring algorithm is proposed. The main idea in this paper is that restore the latent image by nondimensional gaussianity measure regularization, use the T-smooth to extract the salient edge, and use the variational Dirichlet blur kernel estimation to obtain a more accurate motion blur-kernel. For final latent image reconstruction, it combines the merits of both the total variation and super-Laplacian regularization to preserve tiny details. Compared with existing methods, the proposed method is shown to be more effective and robust, leading to a more accurate motion blur-kernel and a better final restored image.
blind deblurring; salient edge; nondimensional gaussianity measure; variation Dirichlet
10.13954/j.cnki.hdu.2017.06.006
2017-01-03
鲍宗袍(1990-),男,浙江温州人,硕士研究生,信息与通信工程.通信作者:陈华华副教授,E-mail:iseealv@hdu.edu.cn.
TN911.73
A
1001-9146(2017)06-0024-06

