大涡模拟中模型系数对方柱绕流的影响
张童伟,聂 欣,陶雪峰
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
大涡模拟中模型系数对方柱绕流的影响
张童伟,聂 欣,陶雪峰
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
采用大涡模拟中3种不同Smagorinsky系数的标准Smagorinsky-Lilly模型和动态模型,对雷诺数为22 000的三维方柱绕流进行数值研究.对计算结果中的特征变量进行了验证与分析;并对不同尺度的涡旋及其相互关系进行研究;同时对流场不同位置处和不同Smagorinsky系数对计算结果的影响及其准确性进行了对比分析.结果表明:不同Smagorinsky系数对流场中的大尺度涡旋以及斯特劳哈尔数的计算结果影响较小;小尺度涡旋的含能量随Smagorinsky值的减小而减小,且较小Smagorinsky系数的模型展现出的小尺度涡旋更多;不同模型的在方柱尾流区不同位置计算准确度存在差异.整体来看,动态模型相比于标准Smagorinsky-Lilly模型更为合适.
大涡模拟;方柱绕流;Smagorinsky系数;动态模型;湍流能谱
0 引 言
方柱绕流广泛存在于环境、海洋、水利、动力机械及建筑等诸多工程领域,其绕流涡旋脱落产生的振动对机械零部件、建筑和桥梁的稳定具有重要影响,涡旋升阻力在海洋方面也得到广泛应用,另外方柱后方的回流现象对泥沙以及污染物的输运起到重要作用.与此同时,由于方柱几何模型简单,且涉及到剪切层的转捩,流动的分离和附着,周期性的涡脱落等复杂的流动现象,因此被广泛应用于实验和数值模拟的研究[1-5].其中大涡模拟作为一种效率高且计算精准的模型被应用于绕流问题的研究.
大涡模拟所用的亚格子模型中Smagorinsky系数一直是研究者们关注的对象.Smagorinsky系数Cs是对亚格子涡粘系数进行描述时引出的一个参数,它与过滤尺寸的乘积称为混合长度.对于Cs系数的确定方法,文献[6]根据经典的局部各向同性湍流理论,在Kolmogorov能谱惯性子区范围内,推导得出的Cs取值范围在0.17~0.21之间;文献[7]通过对一些学者的研究结果进行总结,得出Cs取值范围在0.19~0.24之间;而根据文献[8]对渠道湍流的大涡研究表明,较大的Cs值产生的耗散也大,特别是在近壁区表现得更明显,因此对于内流问题,其建议Cs值在0.1左右较合适;文献[9]采用3种不同的Cs系数来模拟渠道湍流问题,与直接数值模拟DNS的结果比较表明,Cs=0.065时计算结果更准确.近年来的研究表明,Cs不是一个常数,即使对于特定的流动,它也是一个与物理模型和数值计算紧密相关的值,需要在使用中不断调整才能得到合适的结果.而对于绕流问题,文献[10]在进行绕流大涡模拟时采用的Cs值为0.07;文献[11]取Cs为0.12进行计算.而关于Cs系数对三维方柱绕流模拟结果的影响,还没有较为系统的研究.
本文采用不同Cs系数下的标准Smagorinsky-Lilly模型和动态模型对三维方柱绕流进行大涡模拟,计算结果与文献[3-4]的结果进行了对比.研究了方柱下游流场的时均速度、湍流特性及3D流动状态,对比分析了不同Cs系数下Smagorinsky-Lilly模型的差异,同时验证了动态模型在湍流中计算的准确性,对方柱绕流的流动特性进行分析,为湍流问题研究模型的选择和实际工程应用提供有价值的参考.
1 控制方程与模型
1.1 控制方程
运用大涡模拟(Large Eddy Simulation,LES)方法,对连续性和不可压缩流动的Navier-Stokes方程进行滤波,得到如下的控制方程:
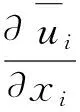
(1)

(2)

(3)
1.2 亚格子模型
要实现大涡数值模拟,必须构造亚格子应力的封闭模式.其中以Boussinesq假设为基础的计算公式如下:
(4)
(5)
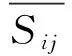
1.2.1 标准Smagorinsky-Lilly模型
标准Smagorinsky-Lilly模型最早是由J. S. Smagorinsky于1963年基于普朗特混合长度模式的原理而提出的[12],将涡粘系数写成以下形式:
(6)

1.2.2 动态Smagorinsky-Lilly模型
动态Smagorinsky-Lilly模型是D. K. Lilly于1992年基于Germano等式提出的动态确定Smagorinsky系数的方法,简称动态模型DCs[13-14].将Germano等式用Smagorinsky模式代入得到:
(7)
采用最小误差法来解决超定问题,对结果进行系统平均得:
(8)

2 数值试验
2.1 算例描述

图1 计算域几何尺寸简图
本文算例以高雷诺数下的方柱绕流为研究对象,采用不同的Smagorinsky系数及动态模型对其进行大涡模拟,计算结果与相关文献的结果进行对比验证.计算区域为20.5D×14D×4D(D为方柱直径),其中方柱上游4.5D,下游15D,如图1所示.入口速度U=0.535 m/s,均匀流动,出口条件为自由流动,四周表面均设为对称边界条件.工作介质为水(密度ρ=998.2 kg/m3,动力粘度μ=1.005×10-3Pa·s),方柱的绕流雷诺数Re=ρUD/μ=22 000.
2.2 网格与计算过程
根据大涡模拟的物理原则,模型第一层网格的y+应小于1.因此,在粘性底层(y+<5)之内,设置了3~5层网格,根据最终计算的收敛结果,壁面处第一层网格y+在0.5~0.9之间.流域截面的网格形态如图2所示,所有模型的网格总数均为320万.采用FLUENT14.0作为求解器,有限体积法离散控制方程,对于压力与速度的耦合采用SIMPLE算法,时间项采用二阶隐式差分,压力项采用二阶迎风格式进行离散,对流和扩散项采用二阶中心差分格式.根据网格尺度和速度尺度设定时间步长,保证每一次迭代都在一个网格范围内[16],此处Δt设置为1×10-3s,每个子步迭代8次后达到所设定的残差值(1×10-3).本算例使用曙光5 000计算机(单节点32核)并行计算.先进行稳态分析,获得较合适的初场后进行瞬态计算,在取样前计算10个的流动周期(以D/U作为一个流动周期),取样后再计算10个以上的流动周期(约为30个涡旋脱落周期),以获得稳定的统计平均结果.其中标准Smagorinsky-Lilly模型的计算时间为140 h,动态模型的计算时间为180 h,由于此模型需要进行二次过滤且在计算过程中不断改变Cs的值,因此需要消耗更多的计算资源,约为标准模型的1.3倍.

图2 计算域网格
3 结果与分析
不同Cs系数和模型下,方柱绕流特征变量的模拟结果与相关文献对比如表1所示,包括时均且展现平均的阻力系数Cd,回流区长度L/D,斯特劳哈尔数St=fD/U,f为通过对升力系数随时间的变化量进行快速傅里叶变换求得的涡旋频率.
从表1可以看出,所有模型的Cd值和实验结果相比都偏大,与前人的研究结果相似,而DCs模型和Cs=0.04时的压力系数值与实验值更接近,其余模型的Cd值随着Cs系数的增加而变大.对于回流区长度的预测,不同的研究者得出的结果有较大差异[1],本文的计算结果与实验值更接近,其中Cs=0.04时的计算结果和实验值对比差异最小,这与阻力系数的值有一定的对应关系.由于亚格子模型只是对小涡进行建模计算,而对涡旋频率起主导作用的大涡在不同Cs系数下的求解方法相同,因此不同模型的绕流St数计算结果基本相同.

表1 特征变量计算结果的对比
3.1 不同模型时均流动特性对比与分析
图3为不同Cs系数和模型下,方柱后方中心线处时均速度u和湍动能K的分布情况.由于在相同网格精度的情况下,亚格子模型的过滤尺度Δ相同,由Cs与Δ的乘积所构成的混合长度值LS不同,使得亚格子的涡粘系数值随Cs值的增大而增大,而较大的涡粘系数会使得流动耗散偏大.因此,在方柱附近位置流动为层流向湍流过渡的区域,应变率张量大而湍流耗散较小[13],较小的Cs值更适合对回流区长度及阻力系数等参数的预测,同时DCs模型在此种流动状态处会自动减小模型系数来修正流动行为[17].从图3中可以看出,Cs=0.04时方柱附近的时均速度与实验值最接近,DCs模型的计算结果也较为精准.由于同时,从回流区最低速度的大小和位置可以看出,不同模型最低速度都位于方柱后方0.85D的距离处,而DCs和Cs=0.04时的最小值分别为-0.098 m/s和-0.009 m/s,与实验值偏差更小.而在远离方柱的位置,由于涡旋的脱落和破碎,湍流耗散较大,此时较大的Cs值更适合此种流动状态.因此对比不同模型在方柱后方较远处的速度恢复值可以发现,Cs=0.18时计算结果与实验值更为接近.
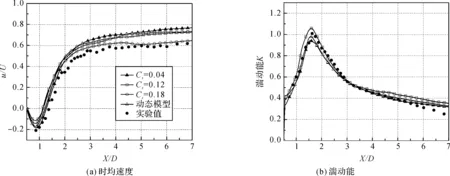
图3 中心线上时均速度和湍动能的分布
从图3明显可以看出,在X/D=1.5的位置存在一个峰值,而此位置为两侧涡旋交替产生的区域,因此速度脉动大.同时,在方柱背面的回流区,由于靠近壁面处的流体以沿壁面的纵向流动为主,在层流底层中由壁面效应而猝发的卷吸涡使得此处速度脉动值较大[18],因此该处的湍动能值也有一个明显的峰值,而Cs=0.18时得到的湍流粘度较大,在此处峰值也更为明显,这与文献[2]和[11]在其他问题的研究中提出的观点类似.综合分析表1中的统计值可以得出,方柱后方较大的速度脉动和较低速度恢复值使得其回流区长度偏小而阻力系数值偏大,从DCs和Cs取0.04和0.12中也可以得到相对应的结论,此结论与文献[2]提出的观点一致.
总之,对于较高雷诺数下方柱绕流的大涡模拟,Cs=0.04时对方柱后方回流区速度场及阻力系数的预测更准确,而较远处的速度恢复值在Cs=0.18时与实验值更吻合,因此,对于局部位置或流动状态较为单一的问题(如渠道流动,管内流动等)进行研究,合理地选择Cs系数对计算结果的精确性至关重要.而对于方柱绕流这种不同位置流动状态差异较大的问题,标准Smagorinsky-Lilly模型很难做到对整个流场的各个位置进行精准预测,此时动态模型更合适.
3.2 方柱绕流涡旋特性分析
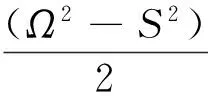

图4 Q准则数分布
在湍流动能输运过程中,大涡占湍动能的绝大部分,因此对数坐标下湍流能谱的含能量主要集中在小波数附近,而小涡占湍动能耗散的绝大部分,在含能区与耗散区之间湍动能通过惯性子区将能量逐级传递下去,此时的湍流能谱函数基本满足波数k的-5/3幂次律[21].特征波数与涡旋尺度及含能量的关系如表2所示,从表2可以看出,大尺度涡旋(小k)在方柱附近位置的含能量最高,随着脱体涡旋的不断发展和破碎,远离方柱的位置,大涡的含能量降低,而小涡整体的含能量增加.由于较小的Cs系数得到的亚格子湍流耗散更小,同时对小尺度涡旋的描述更细致(数量更多),单个涡旋的含能量也会降低,方柱中心线上不同位置的湍流能谱分布情况如图5所示,可以看出小尺度涡的含能量随着Cs系数的减小而减小.而DCs模型的小尺度涡旋含能量在方柱附近位置(X/D=0.5~2.0处)与Cs=0.04相近,在远离方柱位置(X/D=5.0~7.0处)与Cs=0.18相近,这也是DCs模型整体计算结果较为准确的一个重要因素.

表2 特征波数与涡旋尺度、含能量的关系

图5 中心线上湍流能谱的分布
4 结束语
本文通过对大涡模拟中3种不同模型系数Cs的Smagorinsky-Lilly及动态模型对方柱绕流计算结果的影响进行分析得出,不同Smagorinsky系数Cs对流场中的大尺度涡旋以及斯特劳哈尔数St的计算结果影响较小.在流场不同位置出,不同模型对小尺度涡旋及整体计算结果的准确性存在差异.对于方柱绕流这种涡旋尺度与强度变化较大且雷诺数较高的绕流问题,动态模型相比于标准Smagorinsky-Lilly模型更为合适.因此,在今后类似绕流问题的大涡模拟计算中,本文的研究为模型以及模型参数值的选择提供了参考.
[1] RODI W, FERZIGER J H, BREUER M, et al. Status of large eddy simulation: results of a workshop[J]. Journal of Fluids Engineering,1997,119(2):248-262.
[2] SOHANKER A, DAVIDSON L, NORBERG L. Large eddy simulation of flow past a square cylinder: comparison of different subgrid scale models[J]. Journal of Fluids Engineering,1999,122(1):39-47.
[3] LYN DA, EINAV S, RODI W, et al. A laser Doppler velocimetry study of ensemble averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics,1995,304:285-319.
[4] TRIAS FX, GOROBETS A, OLIVA A. Turbulent flow around a square cylinder at Reynolds number 22,000: A DNS study[J]. Computers & Fluids,2015,123:87-98.
[5] ELKHOURY M. Assessment of turbulence models for the simulation of turbulent flows past bluff bodies[J]. Journal of Wind Engineering & Industrial Aerodynamics,2016,154:10-20.
[6] LILLY D K. Representation of small scale turbulence in numerical simulation experiments[J]. Proceedings of IBM Scientific Computing Symposium on Environmental Sciences,1967:195-210.
[7] ROGALLO R S, MOIN P. Numerical simulation of turbulent flows[J]. Annual Review of Fluid Mechanics,1984,16(1):99-137.
[8] DEARDORFF J W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers[J]. Journal of Fluid Mechanics,1970,41(2):453-480.
[9] UDDIN M, MALLIK M S I. Large eddy simulation of turbulent channel flow using smagorinsky model and effects of smagorinsky constants[J]. British Journal of Mathematics & Computer Science,2015,7(5):375-390.
[10] DOOLAN C J. Large eddy simulation of the near wake of a circular cylinder at sub-critical Reynolds number[J]. Engineering Applications of Computational Fluid Mechanics,2014,4(4):496-510.
[11] MURAKAMI S. Overview of turbulence models applied in CWE-1997[J]. Journal of Wind Engineering & Industrial Aerodynamics,1998,74:1-24.
[12] SMAGORINSKY J S. General circulation experiments with the primitive equations, the basic experiment[J]. Monthly Weather Review,1963,91(3):99-164.
[13] LILLY D K. A proposed modification of the Germano subgrid-scale closure method[J]. Physics of Fluids A Fluid Dynamics,1992,4(3):633-635.
[14] GERMANO M, PIOMELLI U, MOIN P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids A Fluid Dynamics,1991,3(3):1760-1765.
[15] 张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008:98-99.
[16] 郑力铭.ANSYS Fluent 15.0流体计算从入门到精通[M].电子工业出版社,2015:43-49.
[17] TU J Y, GUAN H Y, LIU C Q.计算流体力学:从实践中学习[M].沈阳:东北大学出版社,2014:279-281.
[18] 唐鹏,韩省思,叶桃红,等.联合RANS/LES方法数值模拟方柱绕流[J].中国科学技术大学学报,2010,40(12):80-85.
[19] HUNT J C R. Eddies Stream, and Convergence Zones in Turbulent Flows[J]. Center for Turbulence Research CTR-S 88,1988:193-209.
[20] PIOMELLI U, CHASNOV J R. Large-eddy simulations: theory and applications[M]//Turbulence and transition modelling. Springer Netherlands,1996:269-336.
[21] KOLMOGOROV A N. The local structure of turbulence in an incompressible viscous fluid for very large Reynolds numbers[J]. Proceedings of the Royal Society of London,1941,1890(1890):9-13.
LargeEddySimulationofFlowaroundaSquareCylinder:EffectsofSmagorinskyConstants
ZHANG Tongwei, NIE Xin, TAO Xuefeng
(SchoolofMechanicalEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Large eddy simulation of flow around a three-dimensional square cylinder at Re=22000 is performed by using standard model of three Smagorinsky constants and dynamic model, the calculation results of characteristic variable are analysed and validated in this paper. Thus, the different scales vortex and their interrelation are analysed, also the effect of different values of Cs on the calculated result and accuracy is performed in different regions. The results demonstrate that the results of large scale vortex and St number are less affected by the value of Cs, but the energy of small scale vortex decrease with the decrease of the Cs and the model of smaller Cs exhibit more small scale vortex. The calculation accuracy of models is different in different positions of square cylinder. The dynamic model is more appropriate than standard Smagorinsky-Lilly model from overall results.
large eddy simulation; square cylinder; Smagorinsky constant; dynamic model; turbulent spectrum
10.13954/j.cnki.hdu.2017.06.011
2017-05-08
国家自然科学基金资助项目(11472095,50909031)
张童伟(1994-),男,安徽马鞍山人,硕士研究生,流体力学.通信作者:聂欣副教授,E-mail:xin_nie2000@163.com.
O353
A
1001-9146(2017)06-0055-07

