突破一道双层最值检测题的四种视角六种策略
四川省资阳市外国语实验学校 蔡勇全 (邮编:641300)
突破一道双层最值检测题的四种视角六种策略
四川省资阳市外国语实验学校 蔡勇全 (邮编:641300)
1 试题概述
在一次高三数学阶段性检测中,笔者所在的高三备课组以上述题目作为其中的填空压轴题.此题属于双层最值问题,其构思精妙,设计新颖,符合双层最值问题的一贯特征.从评卷结果来看,学生填出正确答案的比例尤其是思维正确率很低,为进一步了解学情,备课组及时做了相应的问卷调查,深入分析后认为,造成这一状况的根本原因是该题表述抽象,学生难以理解求“最值的最值”这样一个循环往复的过程,而且解答所需要的知识面广,方法灵活,技巧性强,具有一定的综合性与难度.本文以该题为例,谈一谈解答此题的四种视角六种策略,供大家参考.
2 求解视角与策略
视角一 借助基本不等式


评述 解法1~3的区别可以从两个方面来看,一是解法1利用了正数条件下的叠乘技巧,而解法2、3利用的是任意实数条件下的叠加技巧,尤其是解法2,还应用了配凑技巧;二是解法1、2分别单独运用了二元、三元基本不等式,而解法3则综合运用了二元、三元基本不等式,从视角一求解对解题者在基本不等式的熟练运用程度方面要求较高.
视角二 化归为“解不等式”的问题
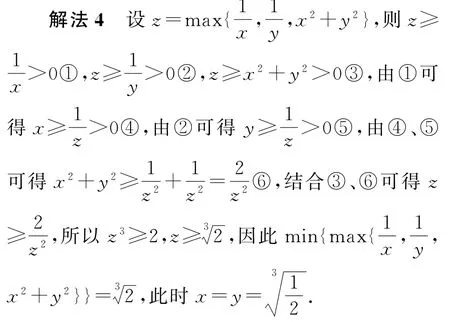
评述 解法4以代数式x2+y2为桥梁,以构造x2+y2所在的范围为立足点,以不等式的传递性为手段,巧妙构造关于z的不等式,对解题者逻辑思维能力要求较高.
视角三 利用“n个正数中的最大(小)值与几何平均数之间的关系”
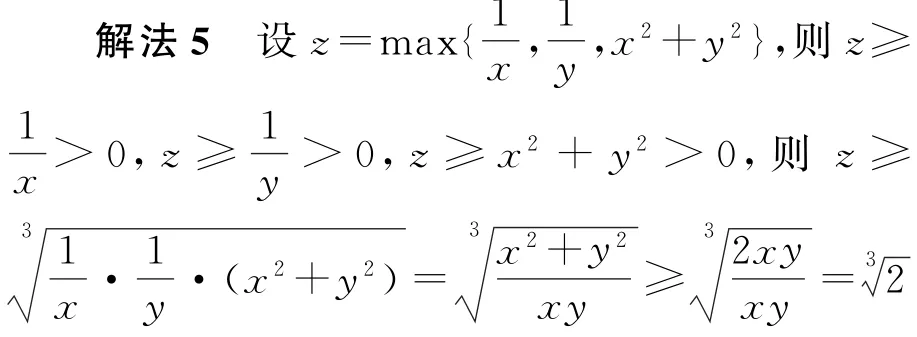
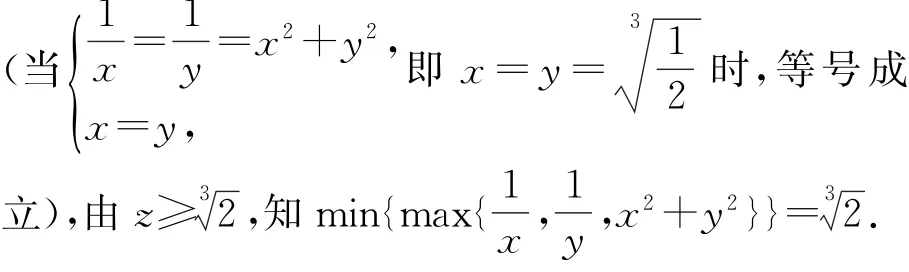
评述 解法5主要应用了“n个正数中的最大(小)值与几何平均数之间的关系”,即“n个正数的最小值不大于这n个正数的几何平均数,n个正数的最大值不小于这n个正数的几何平均数”,对解题者知识面的广博性有一定要求.
视角四 利用分类与整合思想

评述 利用分类与整合思想解决此题,分类对象明确,解题路径清晰,即以最里层的几个研究对象轮流作为最里层的最值进行分析,找出相应条件并在此条件下求出最外层的最值,对解题者思维的缜密性和运算化简能力要求较高.
2017-09-15)

