基于局部最优匹配的斜视SAR子孔径成像算法

孙宁霄 吴琼之 孙 林



基于局部最优匹配的斜视SAR子孔径成像算法

孙宁霄①吴琼之②孙 林*②

①(北京理工大学光电学院 北京 100081)②(北京理工大学信息与电子学院 北京 100081)

斜视合成孔径雷达(Synthetic Aperture Radar, SAR)能够对雷达平台的侧前或侧后方区域进行观测，极大地增加了雷达的探测范围和灵活性。针对斜视SAR子孔径成像，该文提出一种基于局部最优匹配准则的成像算法。该算法在针对某方位频率构造对应的距离徙动校正、2次距离压缩以及方位补偿函数时，以“位于该方位频率处的点目标得到最佳匹配”为准则，不同于传统方法的以“方位中心点获得最佳匹配”为准则，从而能够避免距离方位中心较远的目标的失配，有效地改善了方位边缘区域的聚焦效果。文中通过点目标仿真验证了该算法的有效性。

斜视合成孔径雷达；子孔径成像；局部最优匹配准则

1 引言

本文针对斜视SAR子孔径成像处理，提出一种新的基于局部最优匹配准则的成像算法(Local Optimal Matching Algorithm, LOMA)。该方法首先在方位时域进行距离走动校正，然后基于局部最优匹配准则在方位频域构造徙动校正函数、2次距离压缩函数和方位补偿函数，使得每个目标在其方位频谱中心位置达到最佳校正或补偿，最后利用去斜处理实现方位压缩。该方法可以有效改善方位边缘点目标的聚焦效果。

2 回波信号模型

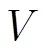
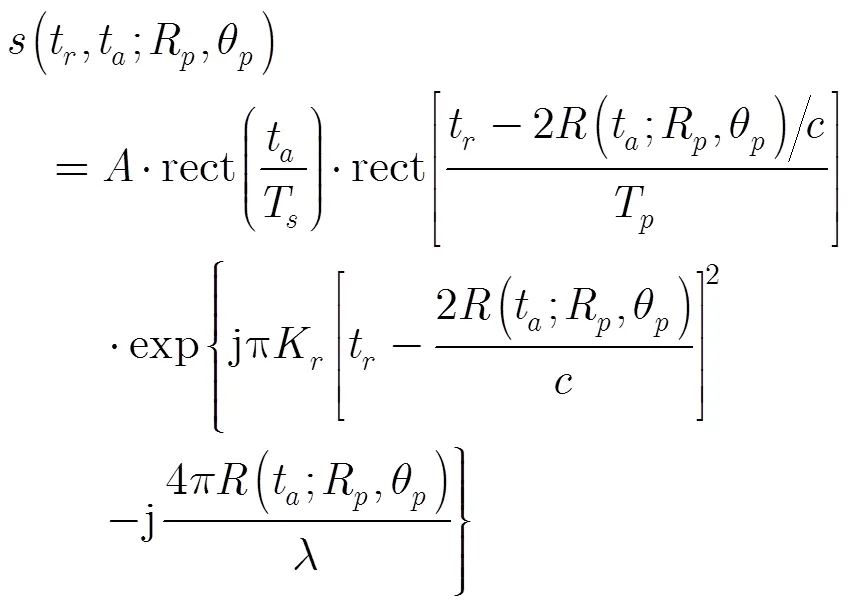
3 LOMA成像算法

LOMA成像算法的处理流程图如图2所示，主要步骤包括距离压缩、方位时域的距离走动校正、方位频域的距离徙动校正及2次距离压缩、方位频域相位补偿以及基于去斜处理的方位压缩，下面对每个成像步骤进行详细介绍。

3.1 距离徙动校正及2次距离压缩

对回波进行距离压缩并采用文献[8]的方法进行距离走动校正后，回波信号的2维频谱可以表示为

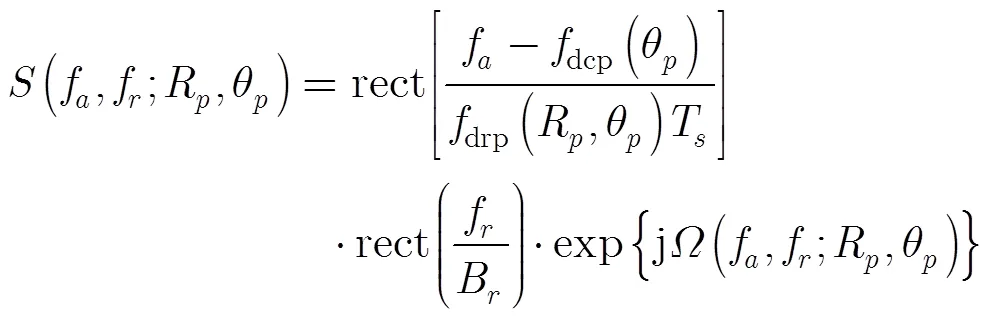
其中，为距离向频率，为方位向频率，为载波频率，为发射脉冲带宽，为点目标的多普勒调频率，为点目标的方位频域支撑域中心频率，支撑域宽度为。和的表达式分别为

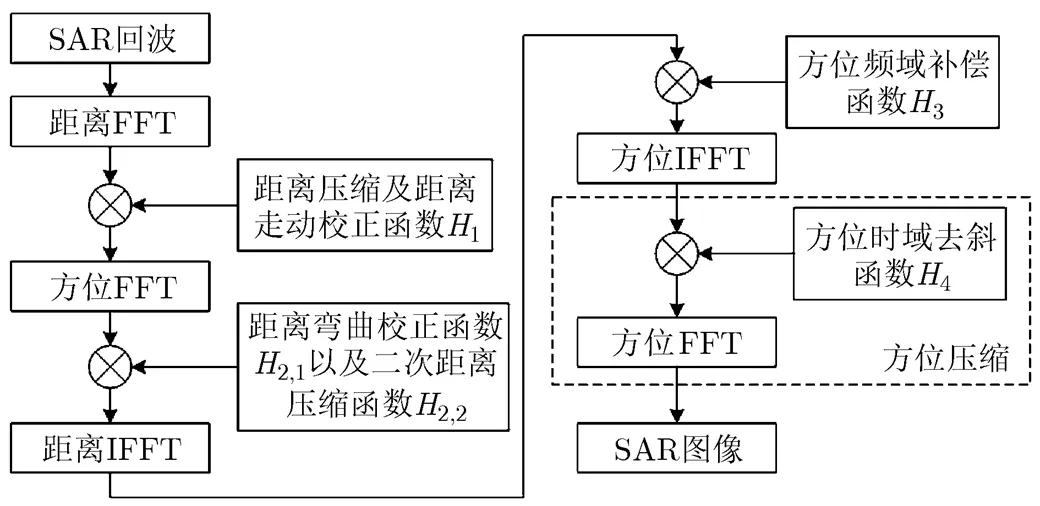
图2 LOMA成像算法的处理流程图

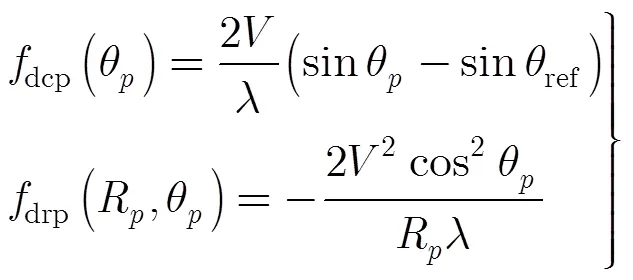
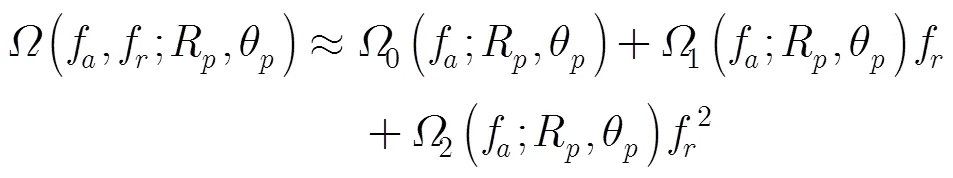
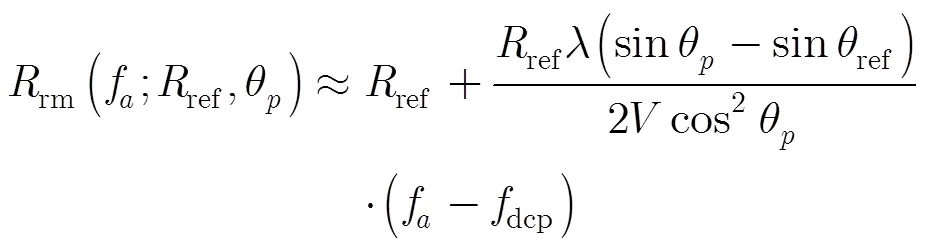
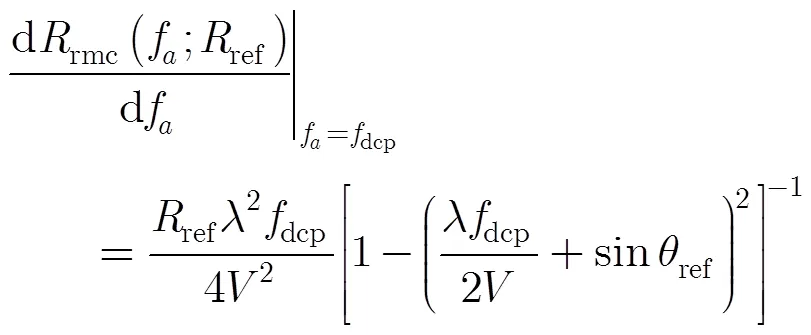
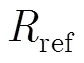
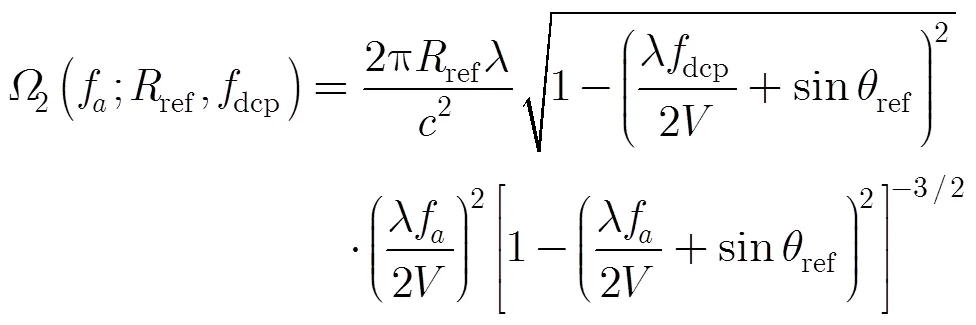
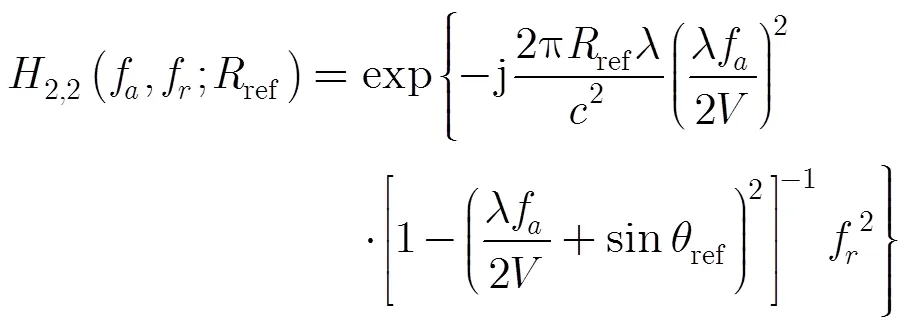
3.2 方位频域补偿

由于是子孔径成像处理，本文采用去斜处理实现方位压缩。如果直接使用SPECAN算法，由于同一距离门内目标的多普勒频率不同，因此部分目标会散焦。如果采用ECS算法中方位压缩方法，由于同一距离门内目标的最短斜距不同，导致匹配函数不同，因此仍会有部分目标散焦。为了实现所有目标的良好聚焦，本文根据局部最优匹配准则构造方位频域补偿函数，使其将该距离门内所有点目标的多普勒调频率修正为相同值，然后再在方位时域采用统一的去斜处理实现压缩。

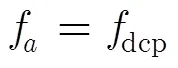
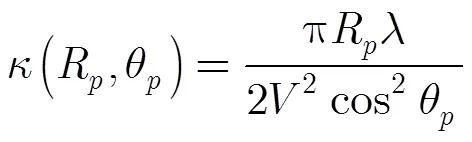
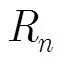
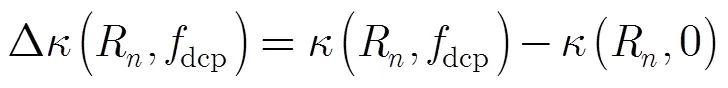
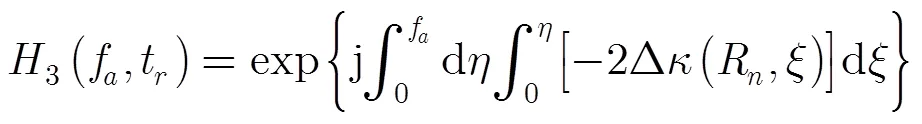
3.3 方位压缩

完成方位频域补偿后，将回波变到方位时域，构造方位去斜函数：

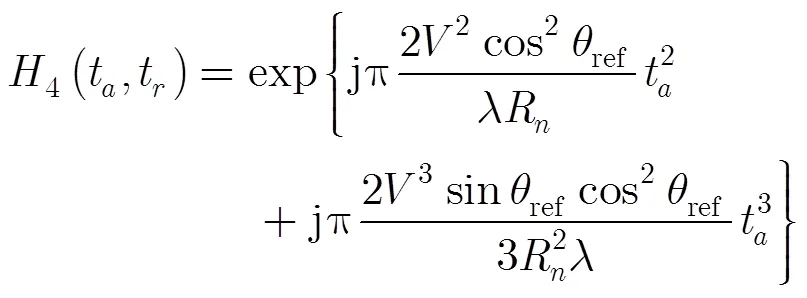
回波乘以去斜函数后，进行方位FFT，完成方位压缩。为了便于理解方位处理的过程，以图1(a)中的3个点目标A, B和C为例，图4直观地给出了LOMA算法方位频域补偿和压缩过程中2次相位的变化。

3.4 算法适用性讨论

任何成像算法都有一定的局限性和算法误差，为了能够在实际应用中选择最佳的成像算法，本小节将对LOMA算法的适用性进行讨论。

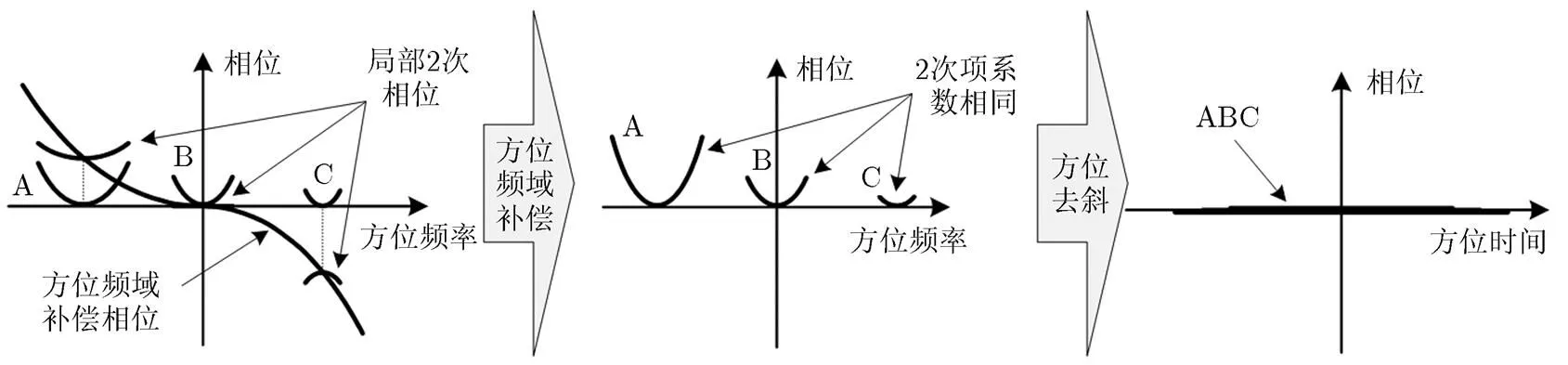
图4 LOMA算法方位频域补偿和压缩过程中2次相位变化示意图

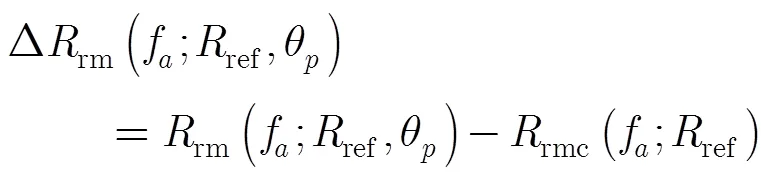
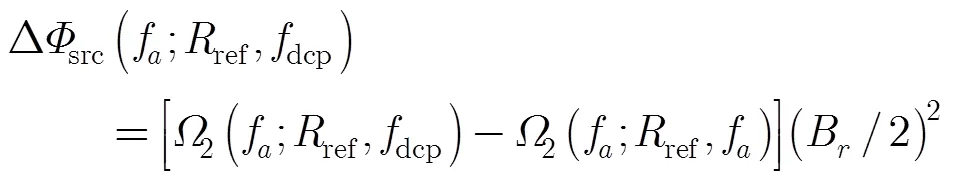
表1斜视SAR子孔径成像处理仿真参数

参数名符号数值 中心斜距20 km 前斜角 速度150 m/s 积累时间6 s 成像区域幅宽3 km 波长0.16 m 带宽65 MHz

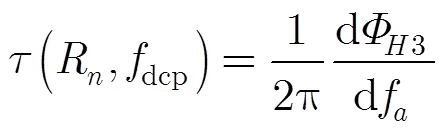
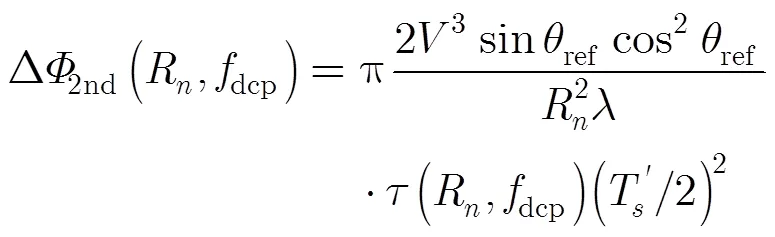
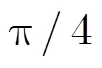
另外，由于子孔径信号已经占满了整个时域支撑域，信号的方位时移会导致信号折叠，在方位FFT时折叠部分的信号无法与未折叠信号相干累加，导致分辨率下降，并产生弱虚假目标。为了解决该问题，需要在方位频域补偿之前，在方位时域补零，扩展时域的支撑域，或者采用类似于文献[15]中方法，通过在方位时域乘以调制相位，影响方位频域补偿函数，将方位时移降低到可接受的范围。

(3)LOMA算法在推导过程中，进行了一些近似，例如忽略了2维频谱中的距离频率3次及更高次相位、方位调制中的3次相位的空变特性以及更高次相位等等。这些近似都会引入一定的相位误差，而且这些误差都会随着分辨率的提高或者成像区域的增加而变大，因此在实际使用LOMA算法时要对这些误差进行分析，以保证其对图像质量的影响在可接受的范围内。

4 仿真结果

4.1 距离徙动校正结果

完成距离压缩和距离走动校正后，3个点目标的距离徙动曲线如图7所示。从图中可以看出，只有方位中心点B的距离走动被校正，位于边缘的A和C则仍有距离走动分量。

为了去除距离走动校正后的残余徙动，在方位频域进行距离徙动校正，图8给出了使用方位中心的距离徙动量进行校正后的结果。从图中看出，点目标A和C大部分距离徙动量都被校正掉了，但是仍没有被完全校直。图9给出了使用本文提出的LOMA算法进行距离徙动校正的结果。从图中可以看出，无论是位于方位中心的点目标B，还是位于方位边缘的点目标A和C，距离徙动曲线都被校直。

4.2 方位压缩结果

图10给出了3个点目标在方位时域的包络和2次相位，其中图10(a)~图10(c)分别为补偿前、ECS算法补偿后、LOMA算法补偿后的包络，图10(d)~图10(f)分别为补偿前、ECS算法补偿后、LOMA算法补偿后的2次相位。在图10(d)中，由于3个点目标的前斜角不同，因此多普勒调频率不同，2次相位的弯曲程度也不同。如果直接进行去斜处理，必然有些点目标会存在残余2次相位，导致方位散焦，所以必须将所有点目标的多普勒调频率修正为同一值，才能进行方位去斜处理。

使用ECS算法进行方位频域补偿后，点目标在方位时域的包络和2次相位如图10(b)和图10(e)所示。从图中可以看出，3个点目标的2次相位的差异变小了，说明ECS算法对多普勒调频率实现了一定的修正，但是仍存在能够产生明显散焦的差异。另外，由于方位频域补偿相位的影响，信号在时域的位置和宽度都有一定的变化。

使用LOMA算法进行方位频域补偿的结果如图10(c)和图10(f)所示。从图中可以看出，点目标的2次相位基本重合，多普勒调频率已被修正为同一值。(这里认为3个点目标仍近似位于同一个距离门，所以多普勒调频率已被修正为同一值。但严格讲，点目标B与其它两个点目标并不在同一个距离门，其多普勒调频率并没有被修正为同一值，存在一定差异，但是差异很小，图中无法显示出来。)

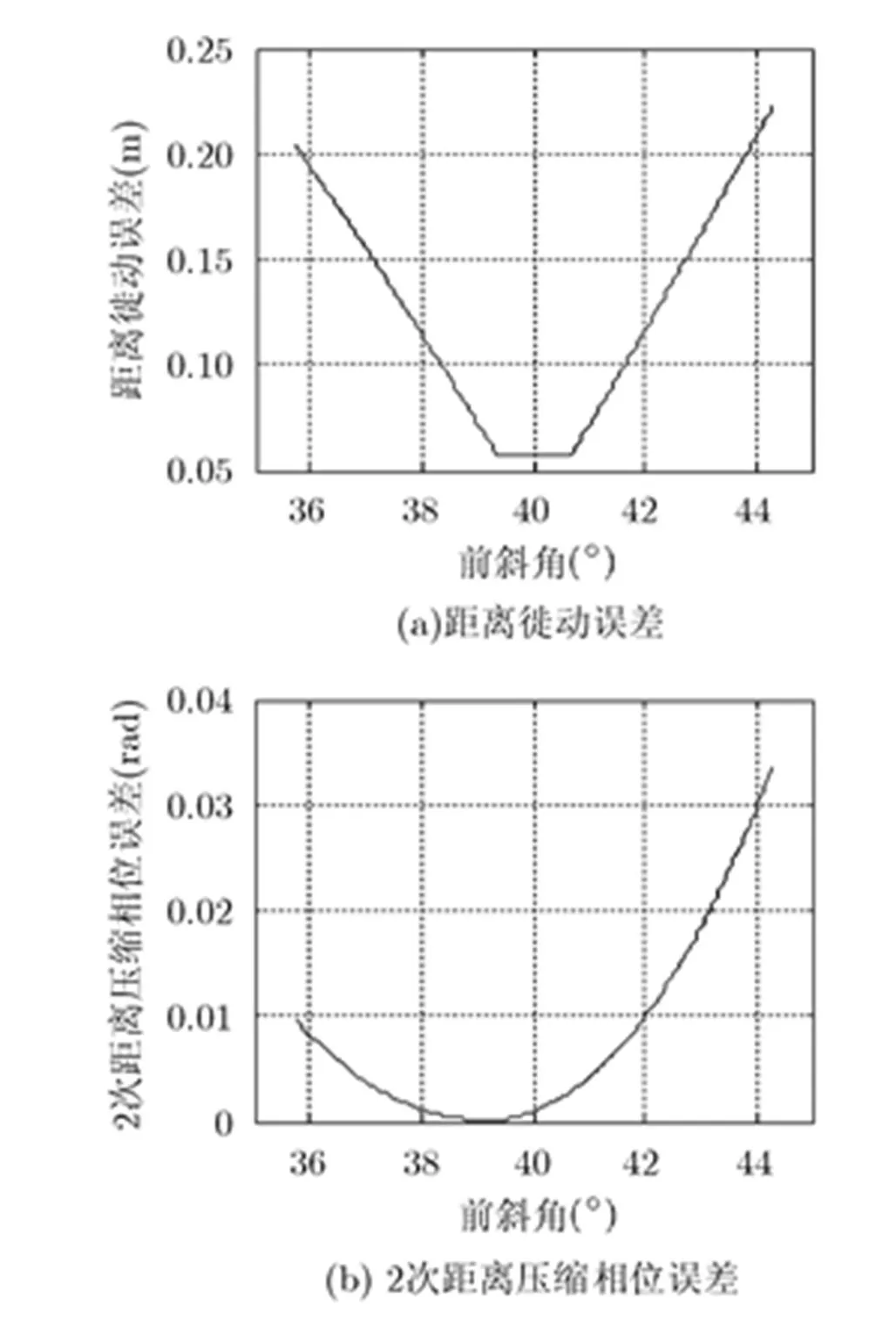
图5 距离徙动误差和2次距离压缩相位误差分析计算结果

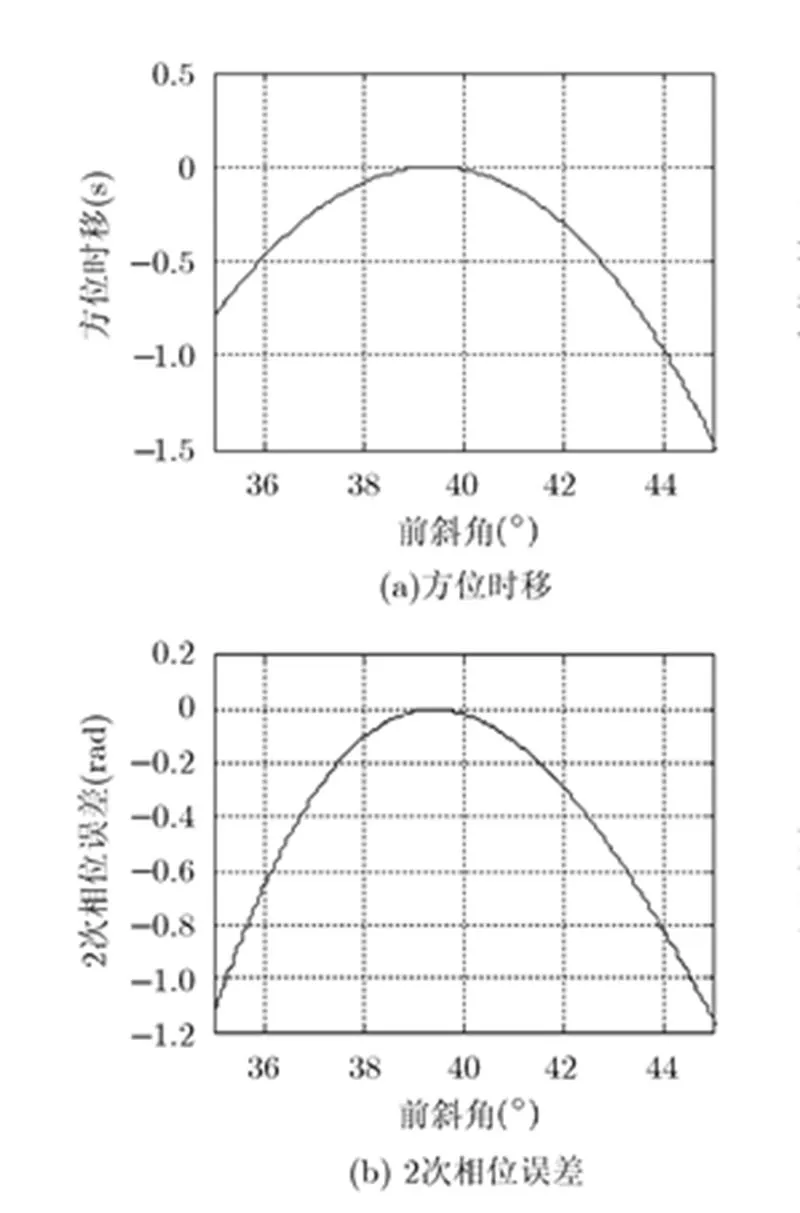
图6 方位频域补偿引起的方位时移和2次相位误差

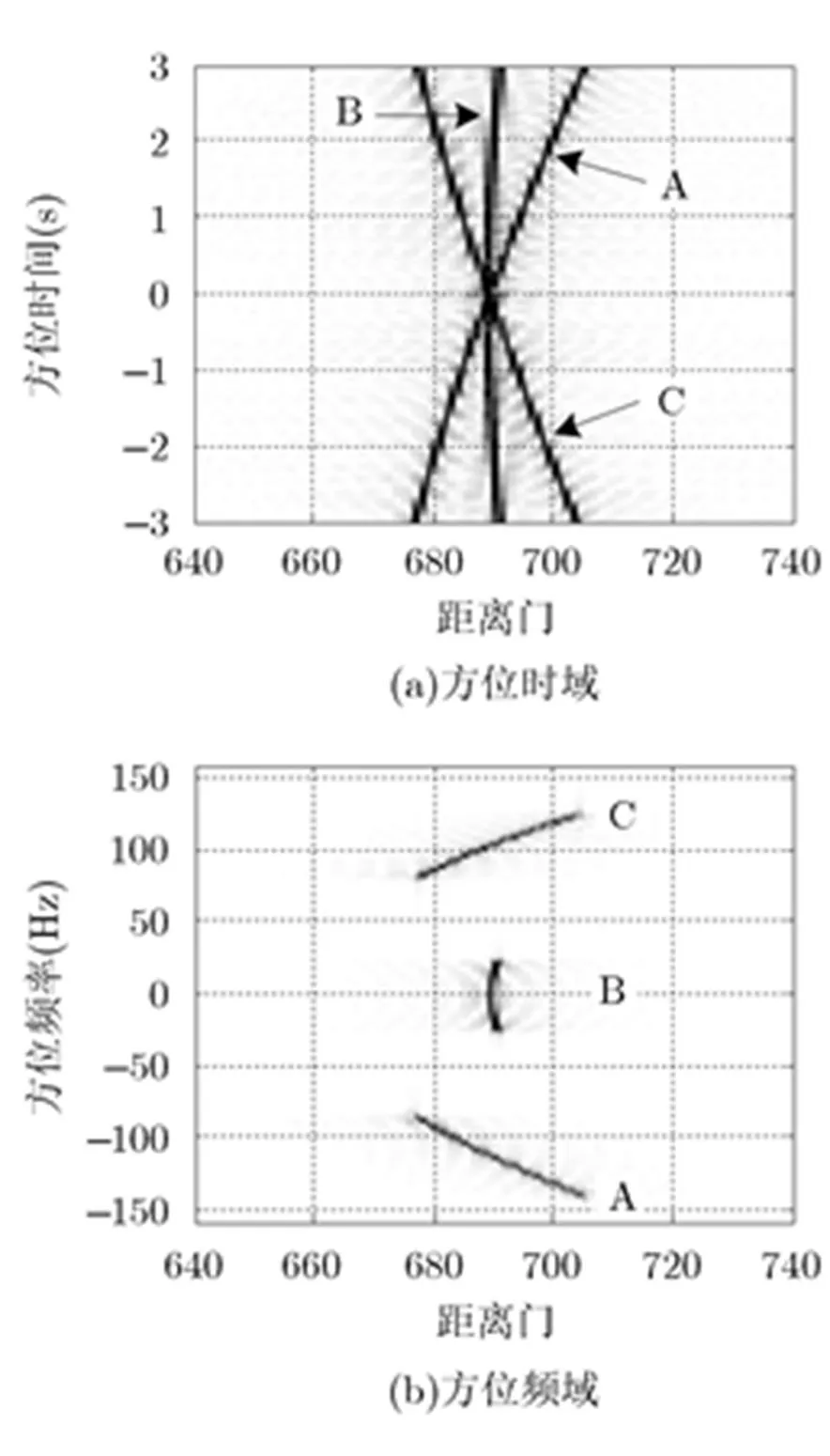
图7 距离走动校正后点目标在方位时域和频域的距离徙动曲线

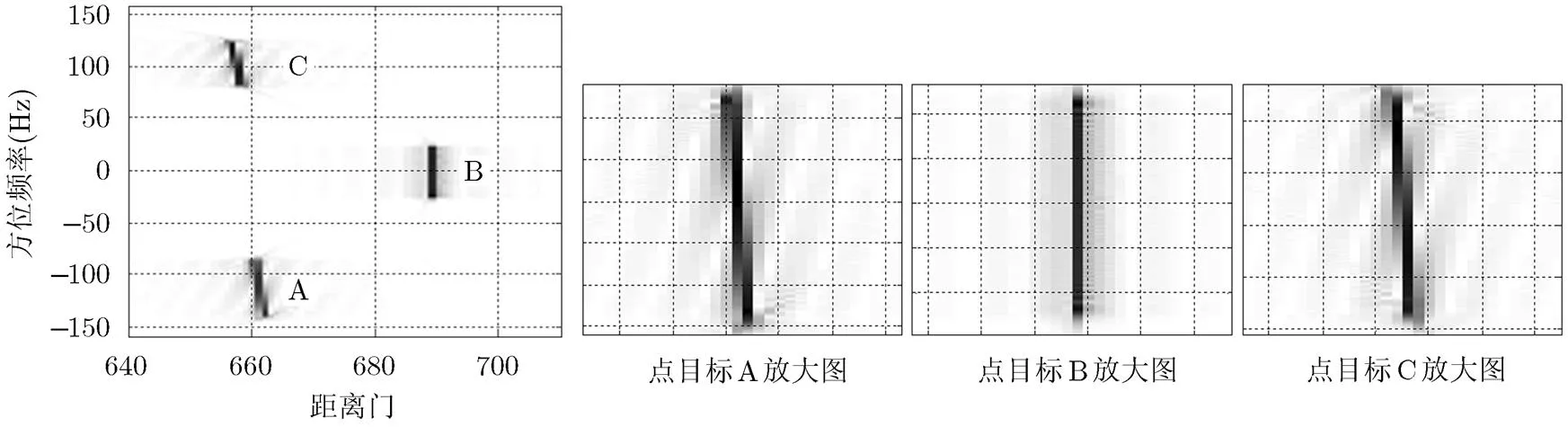
图8 使用方位中心的距离徙动量进行校正后的结果

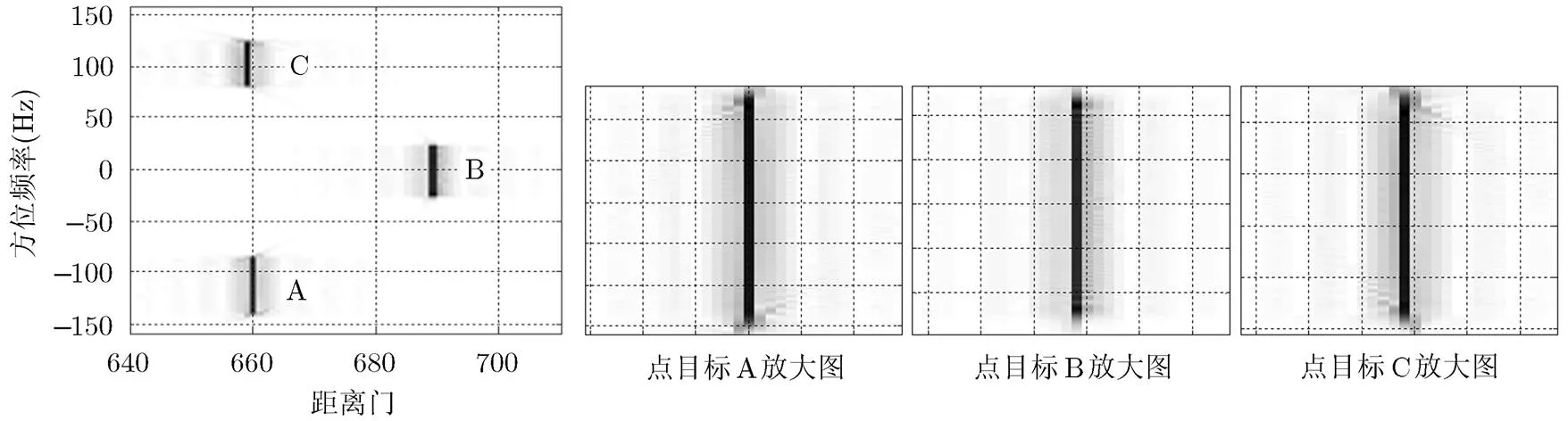
图9 使用LOMA算法的距离徙动量进行校正后的结果

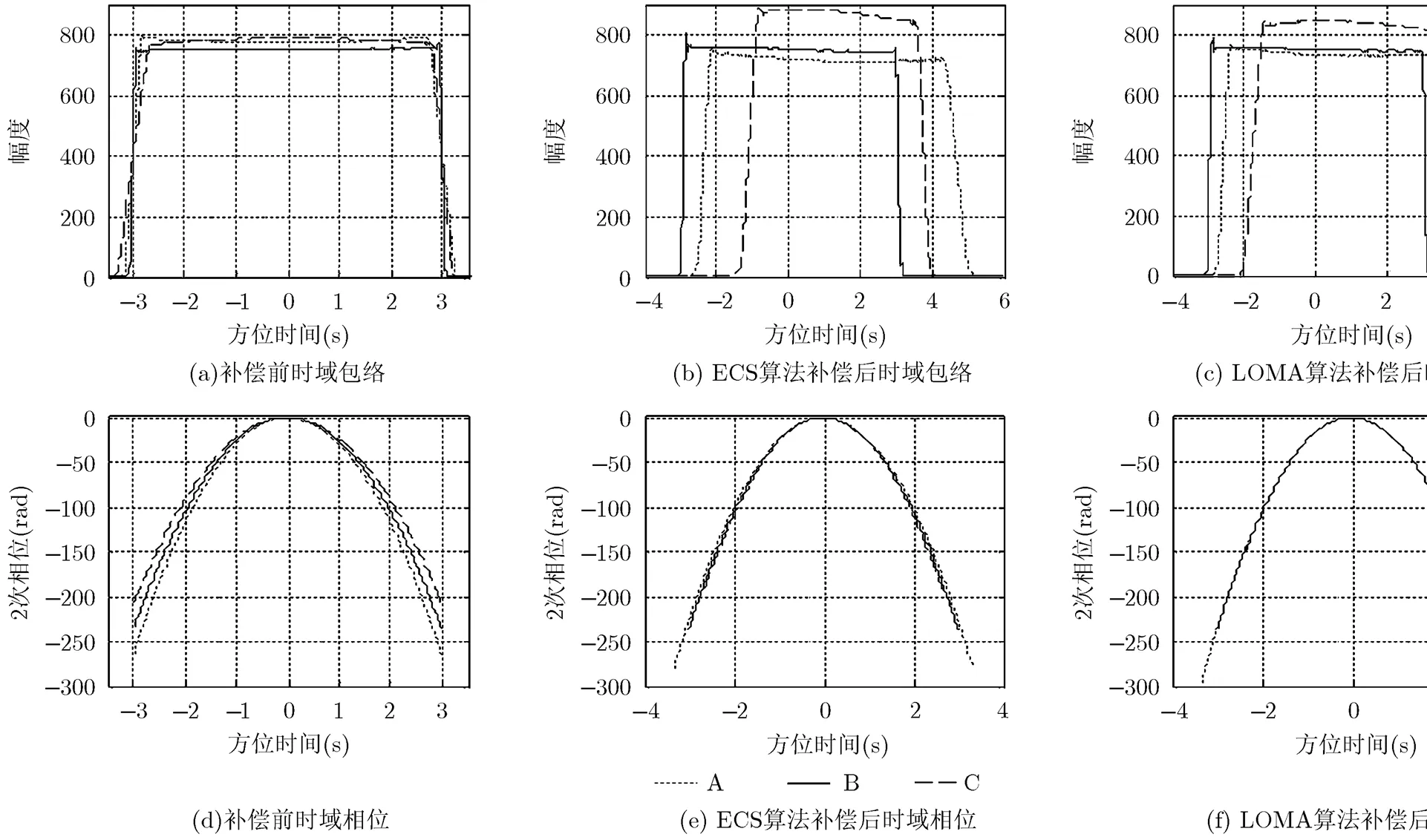
图10 方位频域补偿前后点目标在方位时域的包络和2次相位

图11给出了分别使用ECS算法和LOMA算法获得的点目标地距图像。为了使结果对比更加清晰，图中的点目标图像都进行了升采样处理。从图中可以明显看出，ECS算法方位压缩的结果中，只有方位中心点目标实现了良好聚焦，方位边缘点目标方位向明显散焦，而使用LOMA算法的结果中，方位边缘点目标的聚焦效果得到了明显改善。另外，从图中可以看出点目标的2维旁瓣是相互垂直的，这主要是因为仿真中没有考虑平台高度，多普勒中心不随距离变化，而且方位向采用去斜方式实现聚焦，所以点目标的2维旁瓣是相互垂直的，具体原理可以参考文献[17]中的分析内容。

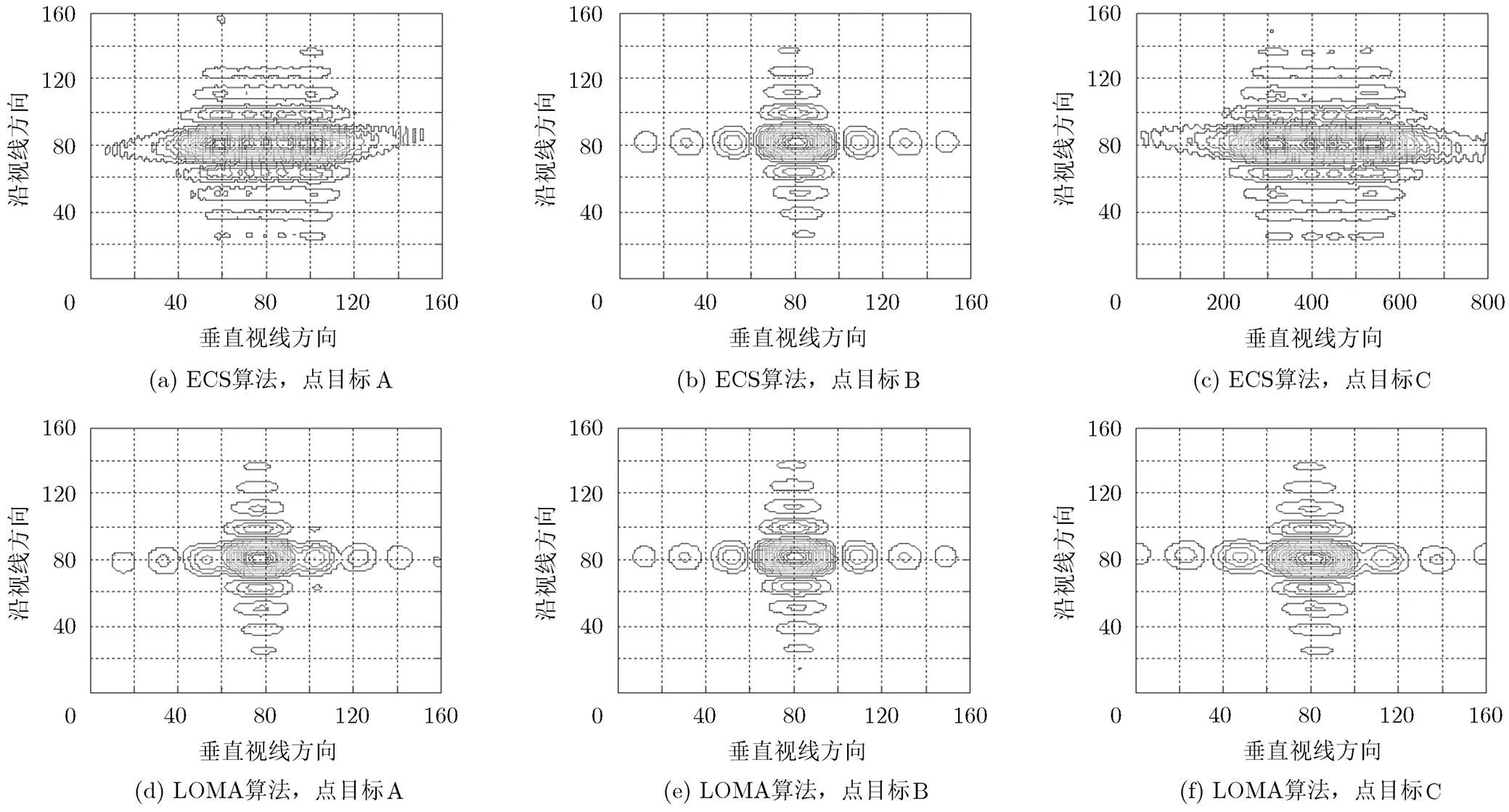
图11 ECS算法和LOMA算法的方位压缩结果对比

对图11中的点目标进行聚焦效果评估(由于ECS算法的点目标A和C散焦太严重，无法进行评估)，地距分辨率、峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)评估结果如表2所示。从表中可以看出，LOMA算法的点目标A和C垂直视线方向有略微散焦，主要原因是方位频域补偿引起的2次相位误差(如图6所示)，点目标的副瓣水平与该2次相位误差相一致。通过减小垂直视线方向的幅宽可以降低该2次相位误差，利用方位加窗处理也可以减弱该2次相位误差对方位聚焦的影响。

5 结束语

本文提出了一种适用于中低分辨率的斜视SAR子孔径成像的LOMA算法，该算法创造性地利用局部最优匹配准则构造成像处理中的匹配函数，能够保证每个目标在其方位频谱中心位置达到距离徙动校正、2次距离压缩和相位补偿的最佳实现，明显改善了方位边缘点目标的聚焦效果。点目标仿真的对比结果验证了LOMA算法的对图像质量的改善效果。本文的LOMA算法之所以能够利用局部最优匹配准则，主要是因为斜视子孔径成像处理具有“同一距离门内点目标在多普勒域支撑域不同”的特点。因此，LOMA算法的适用范围并不局限于斜视子孔径成像，只要具有类似特点的成像模式，例如TOPS (Terrain Observation by Progressive Scans)模式、小子孔径宽波束成像模式等，都可以考虑使用LOMA算法进行成像处理。

表2点目标仿真成像结果评估

成像算法点目标垂直视线方向沿视线方向 分辨率(m)PSLR(dB)ISLR(dB)分辨率(m)PSLR(dB)ISLR(dB) ECSB2.01-13.25-10.212.07-13.21-10.34 LOMAA2.04-10.56-8.502.01-13.56-10.62 B2.06-13.29-10.212.07-13.39-10.40 C2.19-11.62-9.422.06-13.54-10.59

[1] 张澄波. 综合孔径雷达原理、系统分析与应用[M]. 北京: 科学出版社, 1989, 第1章.

[2] CURLANDER C John and MCDONOUGH N Robert. Synthetic Aperture Radar Systems and Signal Processing[M]. New York: John Wiley & Sons, 1991, Chapter 1.

[3] 董祺, 杨泽民, 李震宇, 等. 基于方位空变斜距模型的大斜视机动平台波数域SAR成像算法[J]. 电子与信息学报, 2016, 38(12): 3166-3173.doi: 10.11999/JEIT160785.

DONG Qi, YANG Zemin, LI Zhenyu,Wavenumber- domain imaging algorithm for high squint SAR based on azimuth variation range model [J].&, 2016, 38(12): 3166-3173.doi: 10.11999/JEIT160785.

[4] 聂鑫. 变波门大斜视滑动聚束SAR成像关键技术分析[J]. 电子与信息学报, 2016, 38(12): 3122-3128. doi: 10.11999/JEIT 160812.

NIE Xin. Research on key technique of highly squinted sliding spotlight SAR imaging with varied receiving range bin[J].&, 2016, 38(12): 3122-3128. doi: 10.11999/JEIT160812.

[5] 董祺, 邢孟道, 李震宇, 等. 一种基于坐标轴旋转的俯冲段大斜视SAR波数域成像算法[J]. 电子与信息学报, 2016, 38(12): 3137-3143. doi: 10.11999/JEIT160784.

DONG Qi, XING Mengdao, LI Zhenyu,. Wavenumber- domain imaging algorithm for high squint diving SAR based on axes rotation[J].&, 2016, 38(12): 3137-3143. doi: 10.11999/JEIT 160784.

[6] WONG H Frank and YEO Soon tat. New applications of nonlinear chirp scaling in SAR data processing[J]., 2001, 39(5): 946-953. doi: 10.1109/36.921412.

[7] SUN Guangcai, JIANG Xiuwei, XING Mengdao,. Focus improvement of highly squinted data based on azimuth nonlinear scaling[J]., 2011, 49(6): 2308-2322. doi: 10.1109/TGRS. 2010.2102040.

[8] AN Daoxiang, HUANG Xiaotao, JIN Tian,. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing[J]., 2012, 50(9): 3595-3609. doi: 10.1109/TGRS.2012.2183606.

[9] 刘高高, 张林让, 刘昕, 等. 一种曲线轨迹下的大场景前斜视成像算法[J]. 电子与信息学报, 2011, 33(3): 628-633. doi: 10.3724/SP.J.1146.2010.00575.

LIU Gaogao, ZHANG Linrang, LIU Xin,. Missile-borne large region squint SAR algorithm based on a curve trajectory[J].&, 2011, 33(3): 628-633. doi: 10.3724/SP.J.1146. 2010.00575.

[10] CUMMING G Ian and WONG H Frank. Digital Processing of Synthetic Aperture Radar Data[M]. Norwood MA: Artech House Inc., 2005, Chapter 9.

[11] SACK M, ITO M R, and CUMMING I G Application of efficient linear FM matched filtering algorithms to synthetic aperture radar processing[J].(,), 1985, 132(1): 45-57. doi: 10.1049/ip-f-1:19850006.

[12] MOREIRA Alberto, MITTERMAYER Josef, and SCHEIBER Rolf. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J]., 1996, 34(5): 1123-1136. doi: 10.1109/36.536528.

[13] 李震宇, 梁毅, 邢孟道, 等. 弹载合成孔径雷达大斜视子孔径频域相位滤波成像算法[J]. 电子与信息学报, 2015, 37(4): 953-960. doi: 10.11999/JEIT140618.

LI Zhenyu, LIANG Yi, XING Mengdao,. A frequency phase filtering imaging algorithm for highly squint missile-borne synthetic aperture radar with subaperture[J].&, 2015, 37(4): 953-960. doi: 10.11999/JEIT140618.

[14] 李震宇, 梁毅, 邢孟道, 等. 一种俯冲段子孔径SAR 大斜视成像及几何校正方法[J]. 电子与信息学报, 2015, 37(8): 1814-1820. doi: 10.11999/JEIT141516.

LI Zhenyu, LIANG Yi, XING Mengdao,. New subaperture imaging algorithm and geometric correction method for high squint diving SAR based on equivalent squint model[J].&, 2015, 37(8): 1814-1820. doi: 10.11999/JEIT 141516.

[15] ZENG Tao, LI Yinghe, DING Zegang,Subaperture approach based on azimuth-dependent range cell migration correction and azimuth focusing parameter equalization for maneuvering high-squint-mode SAR[J]., 2015, 53(12): 6718-6734. doi: 10.1109/TGRS.2015.2447393.

[16] 怀园园, 梁毅, 李震宇, 等. 一种基于方位谱重采样的大斜视子孔径SAR成像改进Omega-K算法[J]. 电子与信息学报, 2015, 37(7): 1744-1750. doi: 10.11999/JEIT141383.

HUAI Yuanyuan, LIANG Yi, LI Zhenyu,. Modified Omega-K algorithm for sub-aperture high squint SAR imaging based on azimuth resampling[J].&, 2015, 37(7): 1744-1750. doi: 10.11999/JEIT141383.

[17] LONG Teng, LI Yinghe, and DING Zegang. Interpolation method for geometric correction in highly squint synthetic aperture radar[J].&, 2012, 6(7): 620-626. doi: 10.1049/iet-rsn.2011.0313.

孙宁霄： 男，1987年生，博士，研究方向为合成孔径雷达信号处理及成像算法、极化SAR理论研究与应用.

吴琼之： 男，1977年生，讲师，博士，研究方向为雷达信号处理与存储、合成孔径雷达成像算法.

孙 林： 男，1987年生，助理实验师，硕士，研究方向为合成孔径雷达系统设计、合成孔径雷达实时成像处理.

Local Optimal Matching Algorithm for Subaperture Imagingof Squint Synthetic Aperture Radar

SUN Ningxiao①WU Qiongzhi②SUN Lin②

①(,,100081,)②(,,100081,)

Squint Synthetic Aperture Radar (SAR) can observe the side-front or side-rear scene of the platform. The squint mode improves the observation area and flexibility of SAR greatly. For subaperture imaging of squint SAR, a Local Optimal Matching Algorithm (LOMA) is proposed in this paper. In the algorithm, a new criterion is used in the presentation of the functions for range cell migration correction, secondary range compression and compensation in azimuth frequency domain. The criterion is that the target located at the azimuth frequency is matched optimally. It is different from the traditional algorithm, whose criterion is that the target at the azimuth center is matched optimally. Based on the new criterion, the proposed algorithm is able to avoid the mismatching and improve the focusing of the targets far from the azimuth center. The validity of the proposed algorithm is illustrated by the simulation results.

Synthetic Aperture Radar (SAR); Subaperture imaging; Local Optimal Matching Criterion (LOMC)

TN957.52

A

1009-5896(2017)12-2851-09

10.11999/JEIT170466

2017-05-16；

2017-10-07；

2017-10-27

通信作者：孙林 sunlinrapid@bit.edu.cn