基于内部谐振的弱信号补偿介电目标重构算法
周丽军 欧阳缮 廖桂生 晋良念
基于内部谐振的弱信号补偿介电目标重构算法
周丽军①欧阳缮*①②廖桂生②晋良念①
①(桂林电子科技大学宽带与智能信息技术中心 桂林 541004)②(西安电子科技大学电子工程学院 西安 710071)
对断裂或下沉路基等电大尺寸异质体目标重构其几何特征(如位置,形状,尺寸等),在环境地质等工程应用及市政基础设施维护中尤为重要。然而由于电磁波在目标体内部的衰减,使得目标下表面反射回波很弱。对此该文提出一种基于内部谐振的弱信号补偿目标重构算法。由于有限目标边界的限制,电磁波在目标体内部沿传播方向产生多次反射,此现象在采样时间记录信号上体现为周期谐振。分析了谐振周期与目标宽度的关系并由此估计目标下表面的位置,结合去除虚像以后的目标前表面位置,重构目标形状。实验结果验证了提出方法的有效性以及对噪声的鲁棒性。
目标重构;内部谐振;信号补偿
1 引言
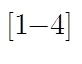
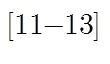
文献[14]分析了埋地倾斜电大尺寸目标在雷达扫描过程中遇到的虚像问题,目标被包裹在虚像中,难以通过曲线位置判断目标真实位置。此外,电磁波穿过介电目标会产生能量衰减,使得目标后表面形成的回波能量很弱,不易被检测到,对此提出一种基于超前/滞后的弱信号补偿方法,对目标后表面回波能量进行补偿,以获取完整的目标几何参数估计。但是此方法只能适用于目标层与其下一层的交界面在探测时间窗范围内的情况,若目标层较厚,在雷达探测时间窗内无法观测到与下一层的交界面,则无法观测到超前/滞后现象。针对此问题,本文提出一种基于内部谐振的弱信号补偿方法,以重构埋地倾斜电大尺寸目标。
2 埋地电大目标扫描机制
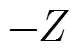
考虑到通常地质探测使用的雷达系统为地表穿透雷达(GPR)系统,而GPR天线辐射电磁波能量会产生一定角度的波瓣,有的主波瓣甚至能达到90°[15]。GPR系统在其位置的正下方采样时间轴上记录接收到的信号,如图1中的点划线即为GPR系统记录信号的采样时间轴。如果没有波瓣,或者将发射电磁波看成是一根射线,那么GPR系统所在位置记录的信号能够反映其位置正下方目标的位置信息,但是因为波瓣(此实验中约为60°)的存在,GPR系统所在位置的采样时间会采集到波瓣范围内的所有信号,这些信号与GPR系统位置下方的目标信号会同时记录到采样时间轴上,使得采集信号会“领先”或“落后”于目标位置。因此,对于一个电小尺寸的目标,这样的扫描机制会在B-scan图像中形成一个顶点在上的双曲线,通过检测双曲线顶点获得目标位置。
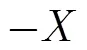
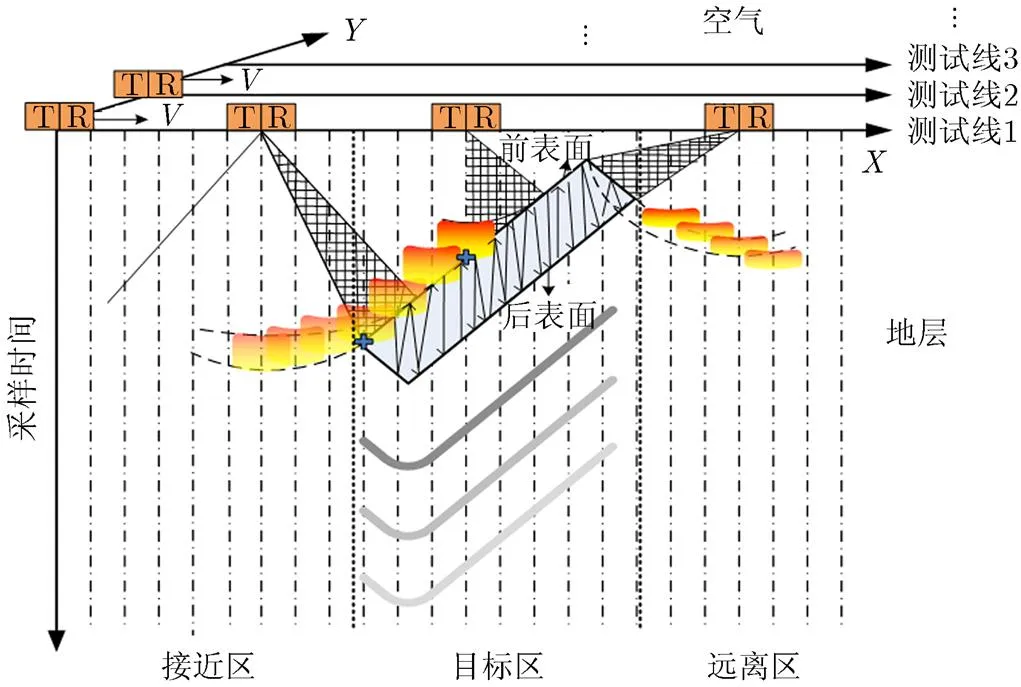
图1 埋地倾斜电大目标回波扫描模型
根据上述分析,对电大倾斜目标的扫描会产生真实目标被干扰散射中心较强能量图像包围的现象,使得目标位置偏离其真实位置,我们称这种干扰图像为虚像。显然为了获取目标的几何信息,需要移除虚像。
此外,对于可穿透的介电目标,电磁波除了从目标的前表面反射回接收天线,还会透射到目标内部从目标后表面反射回接收天线。由于几何扩散,从后表面反射的回波能量非常弱,为了获得整体目标信息,需要增强微弱回波信号。电磁波入射到目标体内部,由于目标体边界的限制,电磁波在目标前表面与后表面来回反射,直至能量衰竭[17],这就导致在采样时间记录信号上形成逐渐衰减的振荡谐波,如图1所示,电磁波在目标体内前表面与后表面之间来回振荡一次,在采样时间上出现2倍目标厚度的谐波,来回振荡两次,出现4倍目标厚度的谐波,如此依次进行,随着电磁波在目标体内振荡次数越多,回波能量越小,而采样时间上出现的谐波周期揭示了目标的厚度信息。
3 目标重构算法
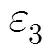
算法步骤如下:
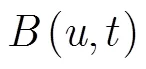
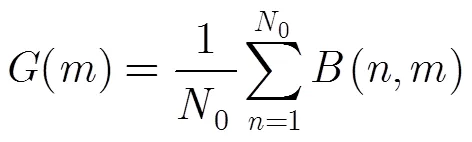
需要注意的是为了保证能提取背景信息,扫描过程中目标不能出现在B-scan的起始位置,通常0=/10。事实上()是前0个A-scan数据的均值;
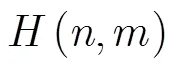
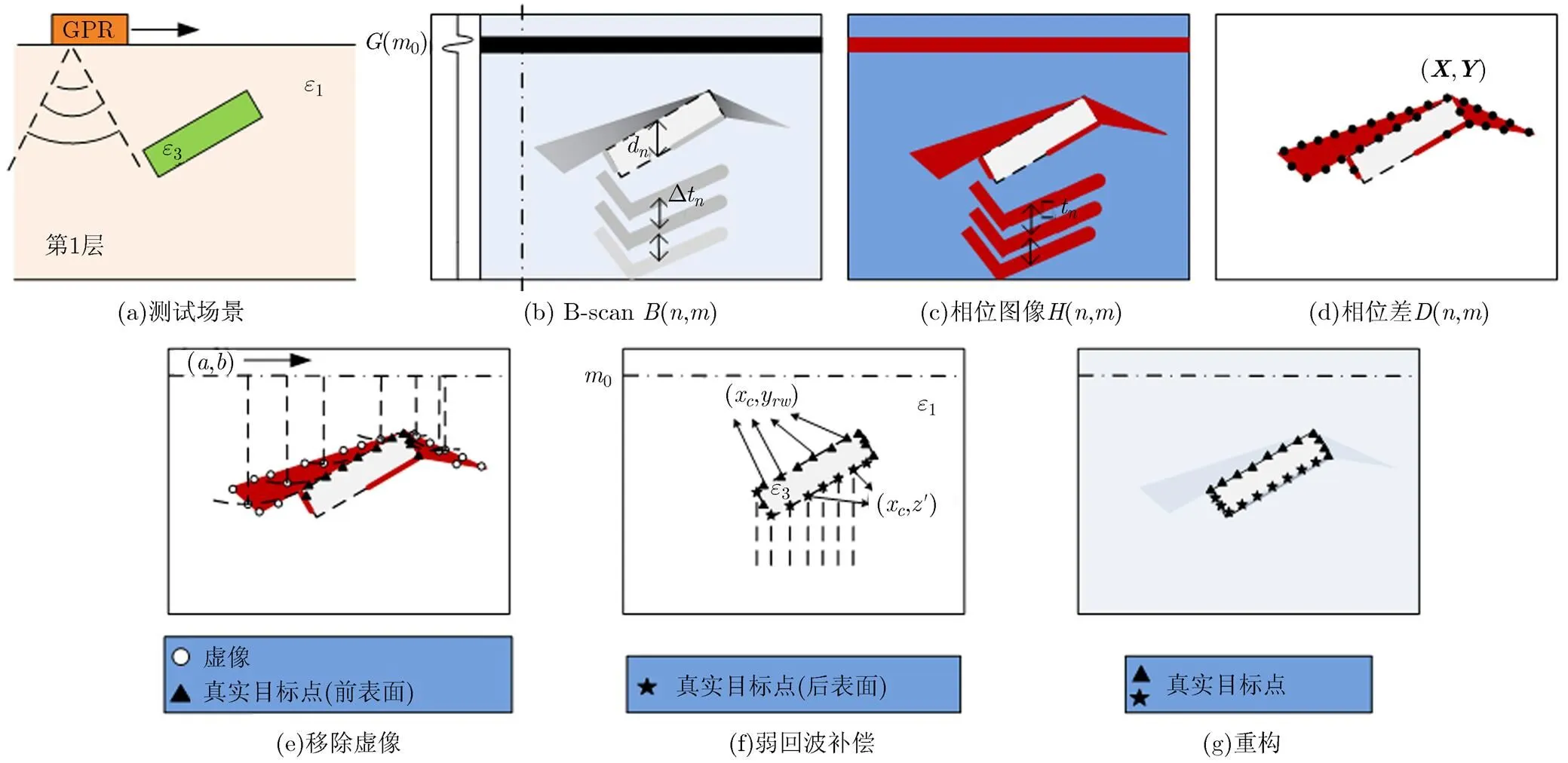
图2 基于介质体目标内部谐振的弱信号补偿方法流程图
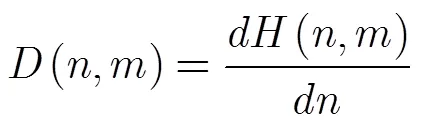
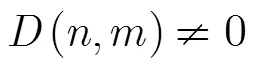
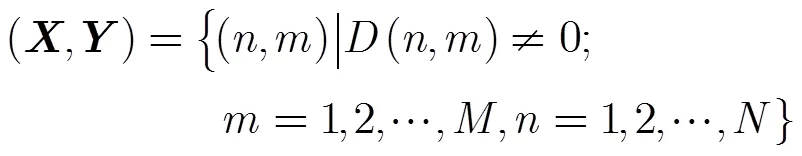
第4步 根据GPR系统的运动轨迹,虚像应该首先出现在接近区,然后出现在目标区,最后出现在远离区,如图1所示。
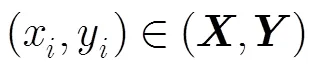
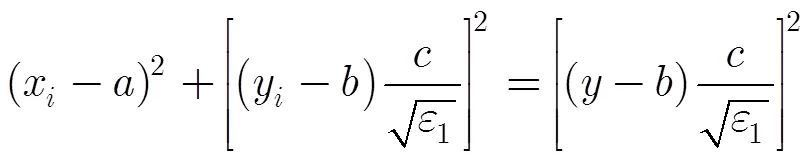
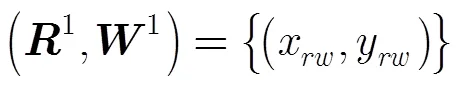
第5步 根据内部谐振与目标厚度的关系,在此给出估计式(5):
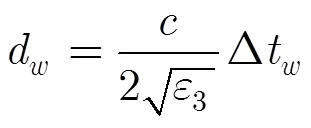
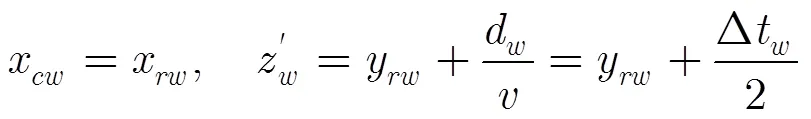
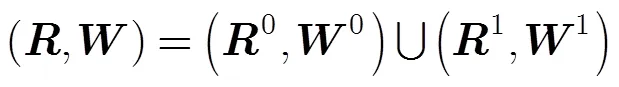
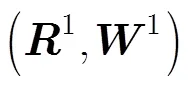
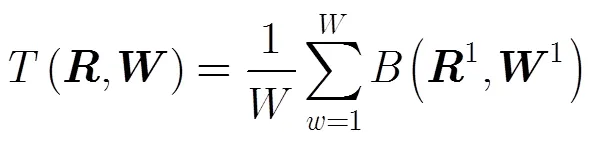
为了移除虚像点,可以将虚像能量赋值为第1步中的背景能量值,即
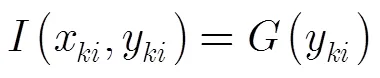
4 实验结果分析
实验在装满干沙的沙坑进行,干沙的相对介电常数为4.25。大小为50.0 cm×45.5 cm×10.0 cm 的水泥板倾斜埋在沙里,如图3所示水泥板的相对介电常数为13.35,详细的参数在图4中给出。单站GPR雷达系统为GSSI公司的SIR-20系列地耦合雷达。天线发射中心频率为400 MHz的瑞克子波,脉冲宽度为2.5 ns。扫描平面被划分为与方向,其中在方向有21条测试线,每条测试线间隔5 cm, GPR系统沿着方向的测试线以1 cm为间隔运动。一个B-scan包含了195个A-scan数据,每个A-scan数据采样256个点。以第11条测试线的B-scan扫描图像为例进行分析。
图5(a)显示了从GPR系统中采集的B-scan能量图像,从图中可以看出,仅从幅值强度很难判断目标的位置,因为有大量虚像点将目标包围,在虚像方框中圈出的较强能量图像往往被误认为是目标的位置,同时在目标下方出现周期谐振。根据第2步与第3步,用希尔伯特变换获取相位信息并进一步根据式(2)提取相位差,如图5(b)中“*”所示。

图3 实测场景
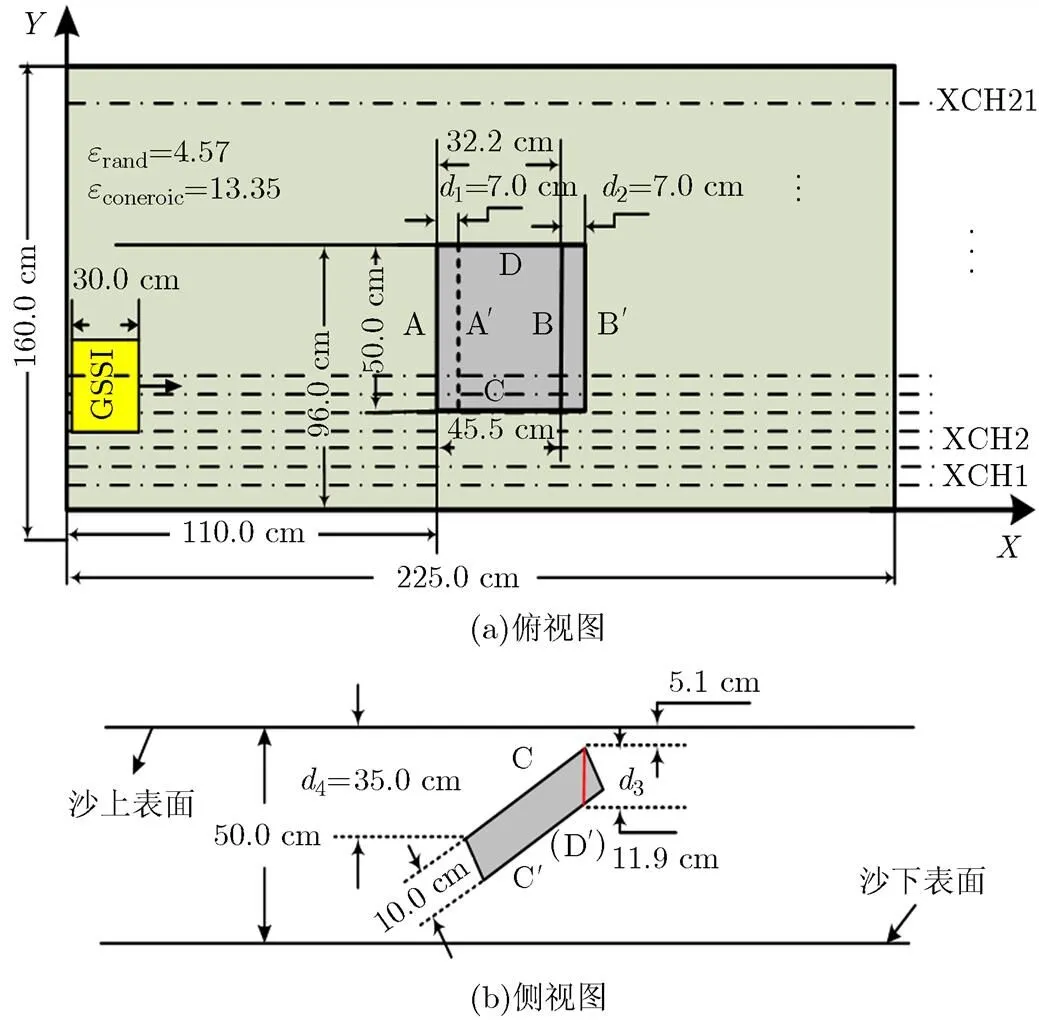
图4 实验场景参数
利用第4步的方法,虚像点与真实目标点能够被区分开,如图5(c)中的“○”与“*”所示。正如所期望的,图5(a)中方框里的强能量图像在图5(c)中被证明是虚像。注意在实验场景中会存在由诸如表面粗糙,非均匀背景,其它散射体等引起的杂波干扰。这些干扰将会在虚像点与真实目标点中产生不合理的点。为了去除这些不合理的干扰点,可以先确定目标所在位置的大致范围。首先,扫描图像中谐振有明显的横向边界,尤其是转换成相位图像以后,更突出了谐振的位置信息,根据谐振出现的横向范围与目标出现的纵向范围可以大致确定整体目标的边界,如图5(c)中黑色虚线方框所示。那么方框外的点则被认为是不合理的点,可以被移除。此外,后表面的补偿点如“★”应该在虚像方框内部。因此,在方框外部的后表面补偿点以及相应的前表面目标点(如图5(c)中的圆圈a, b, c所示)都应被移除。假设分离出的所有真实目标点被看作是目标前表面的点,那么被补偿的应是后表面的点,即使一些后表面的点能够在第4步中被检测到,如图中圆圈d所示。事实上,由其前表面计算得到的补偿点与检测到的d点很接近,几乎重合。这种情况下,检测到的点d也被认为是不合理点而被移除以避免重复。
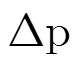
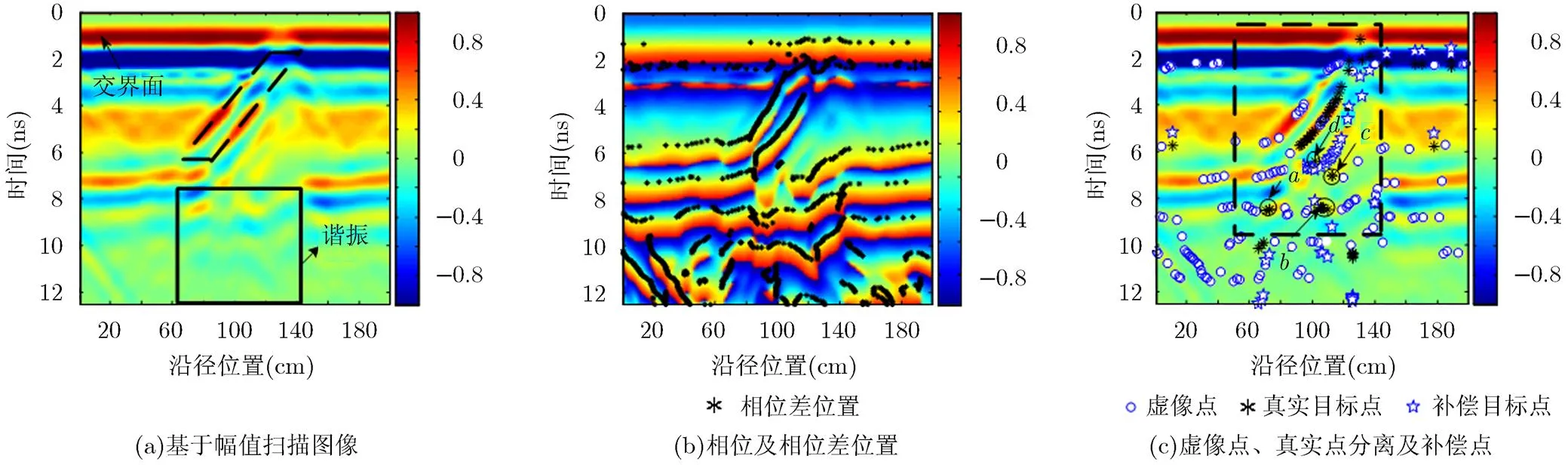
图5 算法第1-第4步结果图像
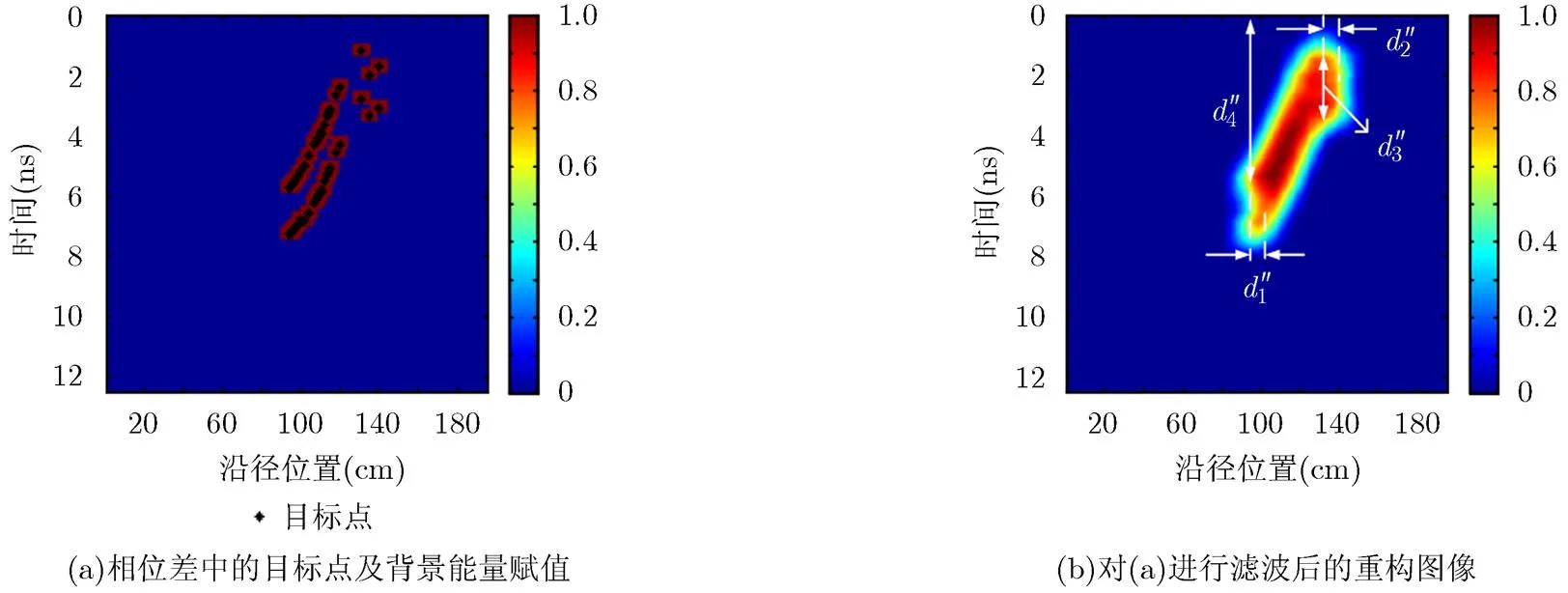
图6 算法第5,第6步处理结果
表1参数重构值与实验值(cm)

1234 真实值7.07.011.935.0 文献[14]中估计值8.08.09.238.8 图6(b)中估计值8.08.013.937.4
5 结束语
本文针对地下深层电大尺寸介电目标的重构问题,在没有目标层与下一层交界面做参考的情况下,提出基于介质体内部谐振弱信号补偿方法。首先利用希尔伯特变换获取幅值扫描图像的相位信息,并进一步得到相位差,从而突出了背景中的变化位置,又消除了背景,将幅值能量扫描图像转换成相位差位置信息。针对虚像问题利用记录信号与来自于目标前或目标后回波之间的几何关系区分真实目标点与虚像点。根据电磁波在目标体内部沿传播方向的多次反射在采样时间记录信号上的谐振表示,分析谐振周期与目标厚度的关系,结合前表面真实目标点位置补偿后表面的弱信号,由此得到完整目标点位置。对利用相位差点表示的完整目标点进行能量赋值,为了平滑背景与目标之间的尖锐边缘,对得到的幅值图像进行多维滤波处理,得到重构目标。通过比较重构目标的几个特殊距离参数与实验设置真实参数,验证了提出的算法的有效性与鲁棒性。
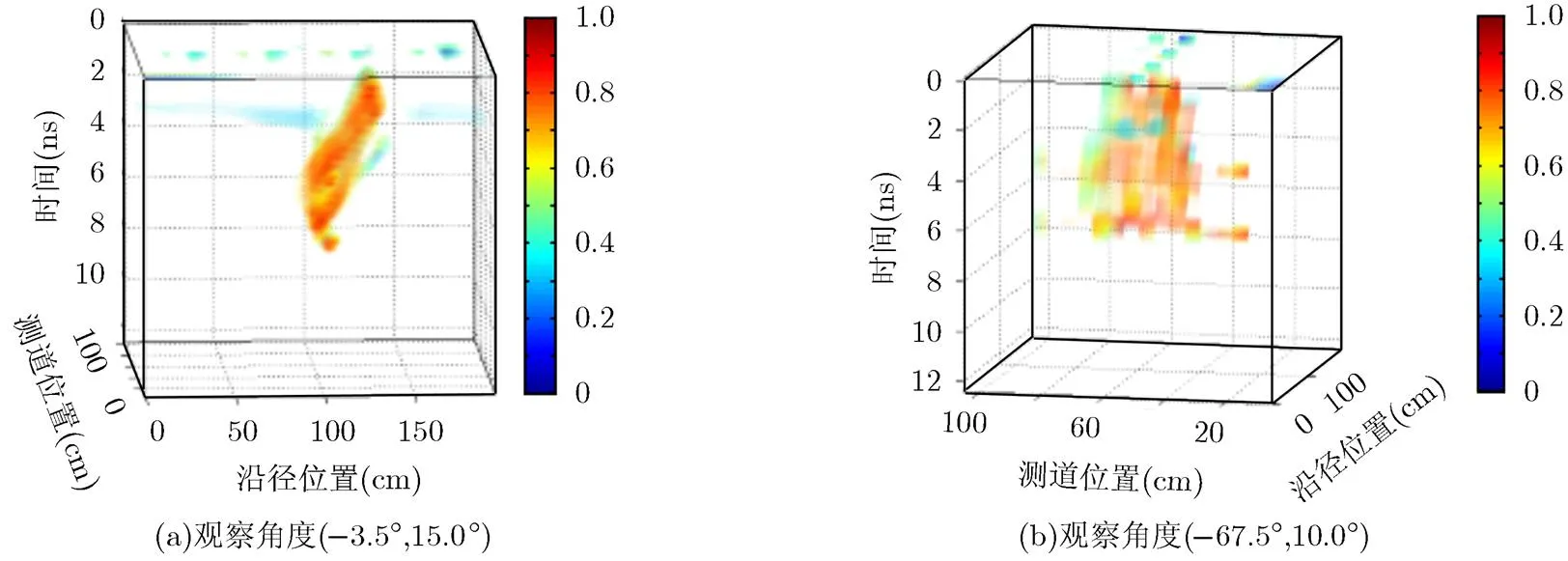
图7 埋地水泥板3D重构图像
[1] DANIELS D J. Ground Penetrating Radar[M]. 2nd Ed., London: The Institution of Electrical Engineers, 2004: 4-5.
[2] WALTON G, LATO M, ANSCHUTZ H,. Non-invasive detection of fractures, fracture zones, and rock damage in a hard rock excavation-experience from the Aspo Hard Rock laboratory in Sweden[J]., 2015, 196: 210-221. doi: 10.1016/j.enggeo.2015.07.010.
[3] SUN M, BASTARD C, PINEL N,. Road surface layers geometric parameters estimation by ground penetrating radar using estimation of signal parameters via rotational invariance techniques method[J].,&, 2016, 10(3): 603-609. doi: 10.1049/iet-rsn.2015.0374.
[4] TETIK E and AKDUMAN I. 3D imaging of dielectric objects buried under a rough surface by using CSI[J]., 2015, 2015: 1-8. doi; 10.1155/2015/179304.
[5] CATAPANO I, CROCCO L, and ISERNIA T. On simple methods for shape reconstruction of unknown scatterers[J].,2007, 55(5): 1431-1436. doi: 10.1109/TAP.2007.895563.
[6] VALERIO G, SOLDOVIERI F, BARONE P M,. Shape reconstruction of scatterers by suitable inverse processing of GPR data[C]. The 6th European Conference on Antennas and Propagation, Prague, 2012: 2209-2211. doi: 10.1109/ EuCAP.2012.6206268.
[7] NOMURA Y, KATO N, NAGANUMA Y,. A geometrical analysis of buried flat-plates on ground penetrating radar images[C]. IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, 2011: 3317-3322. doi: 10.1109/ICSMC.2011.6084181.
[8] SUGAK V and SUGAK A. Phase spectrum of signals in ground-penetrating radar applications[J]., 2010, 48(4): 1760-1767. doi: 10.1109/TGRS.2009.2036163.
[9] HUUSKONEN E, MIKHNEV V, and OLKKONEN M. Discrimination of buried objects in impulse GPR using phase retrieval technique[J]., 2015, 53(2): 1001-1007. doi: 10.1109/TGRS. 2014.2331427.
[10] SOLDOVIERI F, BRANCACCIO A, LEONE G,. Shape reconstruction of perfectly conducting objects by multiview experimental data[J]., 2005, 43(1): 65-71. doi: 10.1109/TGRS.2004. 839432.
[11] MIKHNEV V, OLKKONEN M, and HUUSKONEN E. Identification of buried objects in GPR using phase information extracted from transient response[C]. Proceedings of the 9th European Radar Conference, Amsterdam, 2012: 322-325.
[12] NI X and HUO X. Statistical interpretation of the importance of phase information in signal and image reconstruction[J].&, 2007, 77: 447-454. doi: 10.1016/j.spl.2006.08.025.
[13] PARRELLA G, HAJNSEK I, and PAPATHANASSIOU K P. On the interpretation of polarimetric phase differences in SAR data over land ice[J]., 2016, 13(2): 192-196. doi: 10.1109/LGRS. 2015.2505172.
[14] ZHOU Lijun, OUYANG Shan, LIAO Guisheng,. A novel reconstruction method based on changes in phase for subsurface large sloped dielectric target using GPR[J]., 2016, 134: 36-43. doi: 10.1016/j.jappgeo.2016.08.013.
[15] SKOLNIK M. Radar Handbook[M]. 3rd Ed., New York: Mc Graw Hill, 2008: 3.13-3.15.
[16] SCHOFIELD J, DANIELS D, and HAMMERTON P. A multiple migration and stacking algorithm designed for land mine detection[J]., 2014, 52(11): 6983-6988.doi: 10.1109/ TGRS.2014.2306325.
[17] WANG Z, ZHANG S, and WYROWSKI F. Modeling laser beam propagation through components with internal multiple reflections[C]. Components and Packaging for Laser Systems, California, 2015: 16-1-16-8. doi: 10.1117/12. 2079562.
[18] LU Y and DO M N. Multidimensional directional filter banks and surfacelets[J]., 2007, 16(4): 918-931. doi: 10.1109/TIP.2007.891785.
周丽军: 女,1984年生,博士生,研究方向为超宽带雷达瞬态信号处理、超宽带雷达隐藏目标识别.
欧阳缮: 男,1960年生,教授,博士生导师,主要研究方向为雷达信号处理、自适应信号处理以及通信信号处理等.
廖桂生: 男,1963年生,教授,博士生导师,主要研究方向为自适应信号处理、阵列信号处理、信号检测与估计以及智能天线信号处理技术等.
晋良念: 男,1974年生,副教授,博士,主要研究方向为自适应信号处理、超宽带雷达隐藏目标成像与识别. 收稿日期:2017-04-01;改回日期:2017-09-15;
Target Reconstruction Method for Weak Signal CompensationBased on Internal Resonances
ZHOU Lijun①OUYANG Shan①②LIAO Guisheng②JIN Liangnian①
①(,,541004,)②(,,’710071,)
The geometric characteristics (such as position, shape, size, etc.) of a large size target such as the broken or sinking subgrade are particularly important in engineering applications and municipal infrastructure maintenance. Due to the attenuation of the electromagnetic wave inside the target, the reflection from back surface of the target is too weak to be detected. In this paper, a target reconstruction algorithm for weak signal compensation based on internal resonances is proposed. Due to the limited target boundary, the electromagnetic wave will produce multiple reflections along the propagation direction inside the target. This phenomenon is reflected as periodic resonances in the recording signal. The relationship between the resonant period and the target width is analyzed and the position of the back surface of the target is estimated. The virtual image around the front surface of target is removed by means of phase difference. The whole target shape is reconstructed according to the front surface and back surface of the target. The experimental results verify the effectiveness of the proposed method and the robustness to noise.
Target reconstruction; Internal resonances; Signal compensation
TN957.52
A
1009-5896(2017)12-2844-07
10.11999/JEIT170287
2017-04-01;
2017-09-15;
2017-10-27
通信作者:欧阳缮 hmoysh@guet.edu.cn
国家自然科学基金(61371186, 61162007),广西自然科学基金(2013GXNSFFA019004)
: The National Natural Science Foundation of China (61371186, 61162007), The Guangxi Natural Science Foundation (2013GXNSFFA019004)

