基于自适应趋近律的采摘机器人关节滑模控制研究

袁玉霞，朱小会

(郑州科技学院,郑州 450064)



基于自适应趋近律的采摘机器人关节滑模控制研究

袁玉霞，朱小会

(郑州科技学院,郑州 450064)

利用离散趋近律设计的滑模控制可有效抑制滑模控制中的抖动现象，但其抑制抖动的效果与离散趋近律的设计参数及系统的采样时间有着密切的关系。为此，在分析指数趋近律抖动的基础上，提出了一种自适应滑模控制器，MatLAB能够进一步的提高基于趋近律的滑模控制器的抖动抑制能力。为了验证本文所提出方法的有效性，在MatLAB中实现了该算法，并利用其来控制采摘机器人关节的伺服电机。仿真结果表明：本文所提的算法具有较好的位置跟踪能力，进一步地抑制了指数趋近律滑模控制中存在的抖动现象，提高了系统的性能。

离散趋近律;自适应滑模;采摘机器人;位置跟踪;抖动

0 引言

采摘机器人收获水果和蔬菜所用自动化装置，具有降低工人劳动强度、提高劳动舒适性、提高果蔬采摘的质量、降低采摘成本、提高劳动生产率等特点,因此受到学者们的广泛关注[1-5]。

采摘机器人机械臂建立的控制模型中包含非线性不确定项和未知外界干扰等因素，会影响到系统的控制性能和稳定性。为了解决这一问题，学者们对其进行了深入的研究，并提出了许多行之有效的解决措施[6-9]。

近年来，由于滑模控制具有算法简单、鲁棒性强、可靠性高和响应速度快等特性，被广泛的应用于伺服电机的控制中[10]。但是，由于开关的时间滞后、开关的空间滞后及系统惯性等因素的存在，使得滑动控制在滑模运动中伴随着高频振动[11]，不仅会影响到系统的性能，增加能量的消耗，严重的会破坏系统的元器件[12]。为了抑制系统中存在的抖动现象，学者们进行了深入的研究，常见的方法有趋近律[13]、基于智能算法的滑模控制[14]、观测器法[15]、准滑模控制[16]、动态滑模控制[17]、基于滤波器的滑模控制[18]及切换增益法[19]等方法。利用离散趋近律设计的滑模控制可有效抑制滑模控制中的抖动现象，但其抑制抖动的效果与离散趋近律的设计参数及系统的采样时间有着密切的关系。

本文在分析指数趋近律抖动的基础上，提出了一种自适应滑模控制器，并将其用于采摘机器人关节的伺服电机轨迹控制中，该控制器能够进一步提高基于趋近律的滑模控制器的抖动抑制能力，从而提高系统的性能。

1 草莓采摘机器人结构

本文设计了一种具有五自由度关节型草莓采摘机械手臂，主要包括腰转、肩转、肘转、腕转和腕摆，机器人本体的设计采用跨垄四轮行走机构，动力装置采用伺服电机，如图1所示。在四轮行走机构上安装五自由度机械手臂，用伺服电机作为动力源，使机械手臂达到指定位置。

图1 关节型草莓采摘机械手臂

2 滑模控制器设计

2.1 趋近律

我国高为炳院士提出在确保滑模存在条件的情况下，可利用趋近律的方法来抵制滑模控制中存在的抖动问题，常见的趋近律有等速趋近律、指数趋近律、幂次趋近律及一般趋近律4种，而于指数趋近律而言是应用最为广泛的，则有

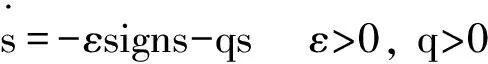
(1)

其中，滑模的趋近速度与参数ε有着密切的关系，趋近速度从一个较大的值逐步变为0 ，使得到切换面时的运动速度很小，从而抑制了控制中存在的抖动。调整参数ε不仅可以保证系统的控制品质还可以减少控制信息中的高频变化。但是，对于离散指数趋近律而言，其不能收敛于零点而是在零点附件来回穿越从而形成抖动。因此，本文针对离散指数趋近律，在分析产生抖动的原因后，提出相应的改进算法。

2.2 指数趋近律抖动分析

如果采样时间非常的小(T<<1.0)，那么指数趋近律的离散形式为

s(k+1)=(1-qT)s(k)-εTsgn(s(k))

(2)

(3)

联合式(2)和式(3)可得

|p|

(4)

针对式(3)所示的趋近律，可分以下3种情况来讨论其收敛性。

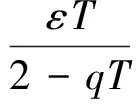
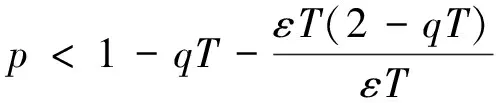
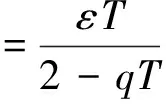
综合上述在各情况的分析，可以得到要使s(k)收敛的充分条件为

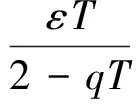
(5)

由上述分析可知，当参数k→∞时,滑模控制的稳态振动幅值为

(6)

从式(6)可以看出：滑模控制进入稳态振动阶段发后，其稳态振动幅的大小与参数ε,q,T有着密切的关系,特别是参数ε,T对其的影响较大。

3 自适应滑模控制器设计

如式(1)所示的离散形式，其参数ε对其影响相当的大，减少ε的值可以降低滑模控制的抖动，但会影响到滑模控制的收敛时间；增大ε可以加大滑模控制的收敛，但在接近滑模面时因速度过快，会引起抖动。因此，理想的ε的值应该是一个变 化的，但运动初期可以拥有一个较大的值，以加快其运动速度，当接近滑模时ε的值应该降低。

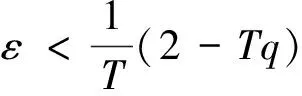
(7)

设计参数为

ε=|s(k)|/2

(8)

如果采样时间能够满足下式

(9)

那么式(7)必须成立。

由式(2) 和式 (8),改进的离散趋近律为

(10)

对于离散系统x(k+1)=Ax(k)+Bu(k)而言,如果CB≠0成立，那么其控制律应该为

(11)

其中，s(k)=Cx(k)。

改进控制算法稳定性分析，则有

(12)

(13)

由式(12)和式(13)可知，改进后的指数趋近律是稳定的。

4 数字仿真

为了验证本文所提出方法的有效性，在MabLab中实现了该算法，并利用其来控制并联机床的支路中的伺服电机。伺服电机的离散状态空间方程为

x(k)=Ax(k-1)+B(u(k-1)+d(k-1))

(14)

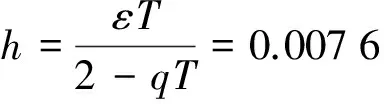
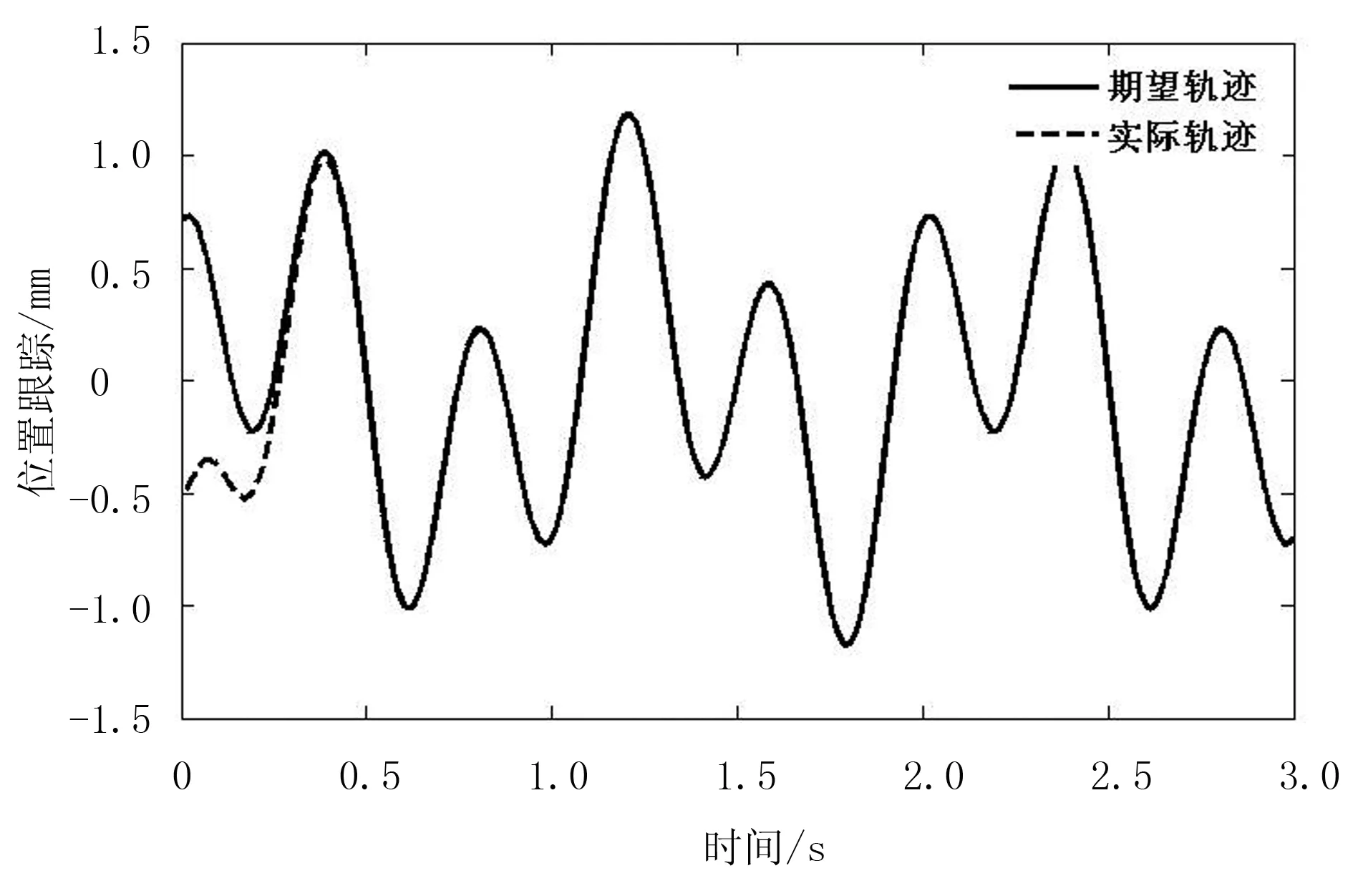
图2 指数趋近律滑模控制位置跟踪

Fig.2 Position tracking of sliding mode control with exponential reaching law

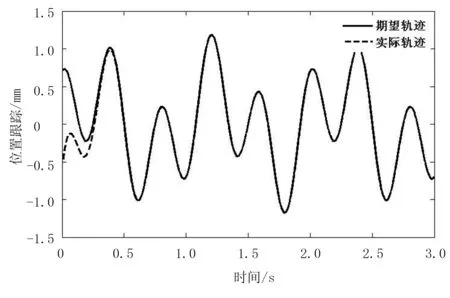
图3 本文算法制位置跟踪

图4 指数趋近律滑模控制控制输入

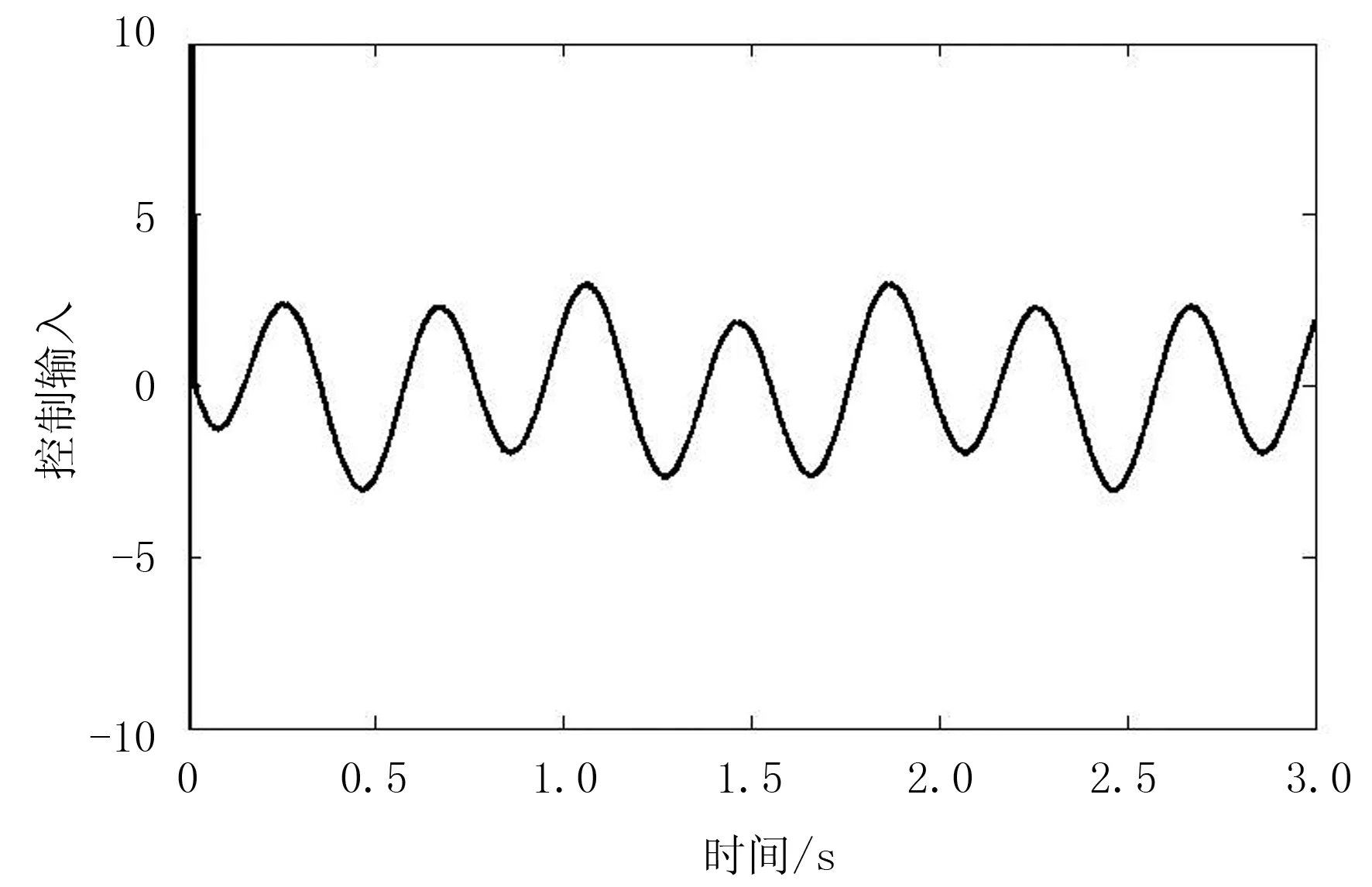
图5 本文算法控制输入

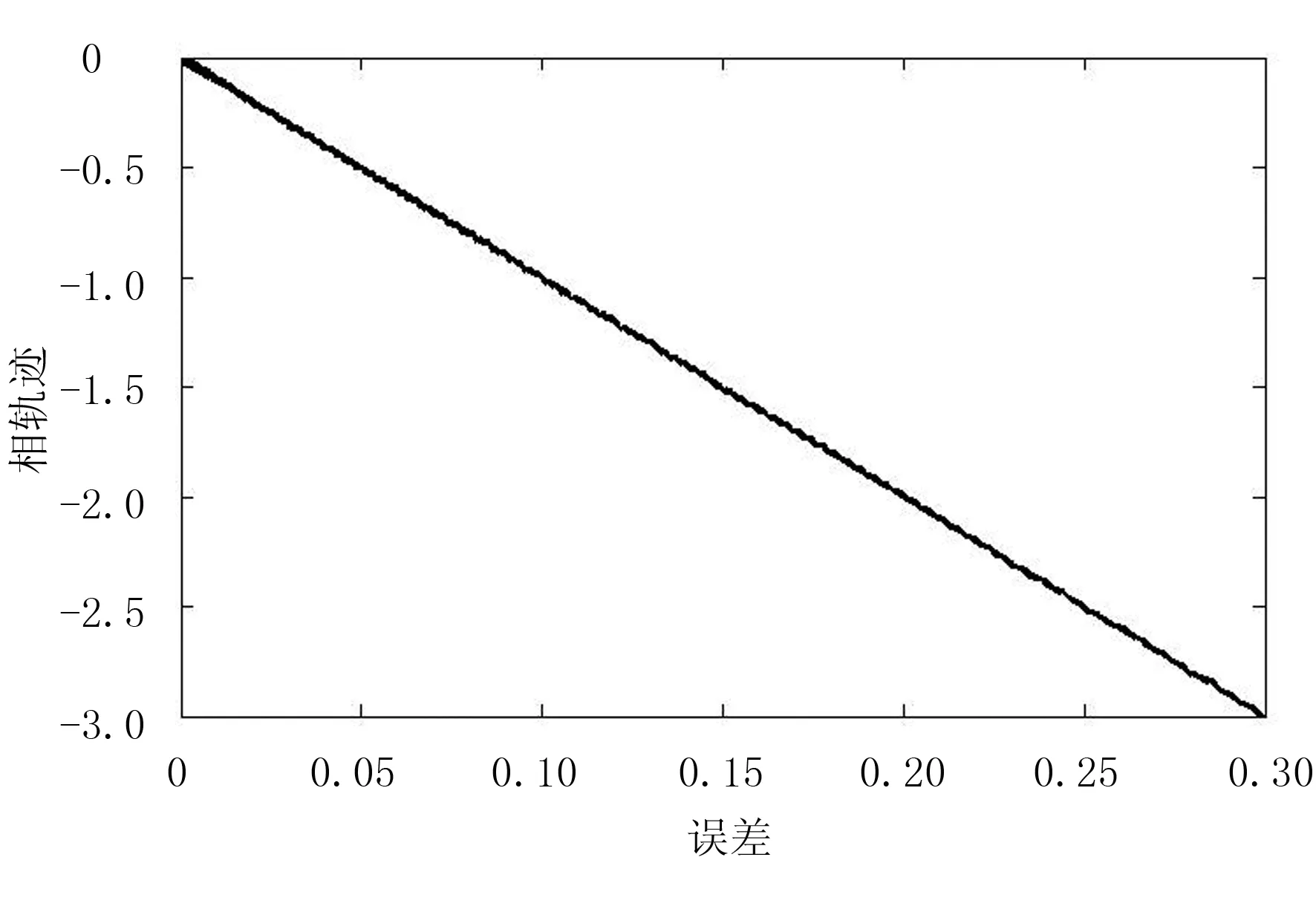
图6 指数趋近律滑模控制相轨迹

Fig.6 Phase trajectory of sliding mode control with exponential reaching law

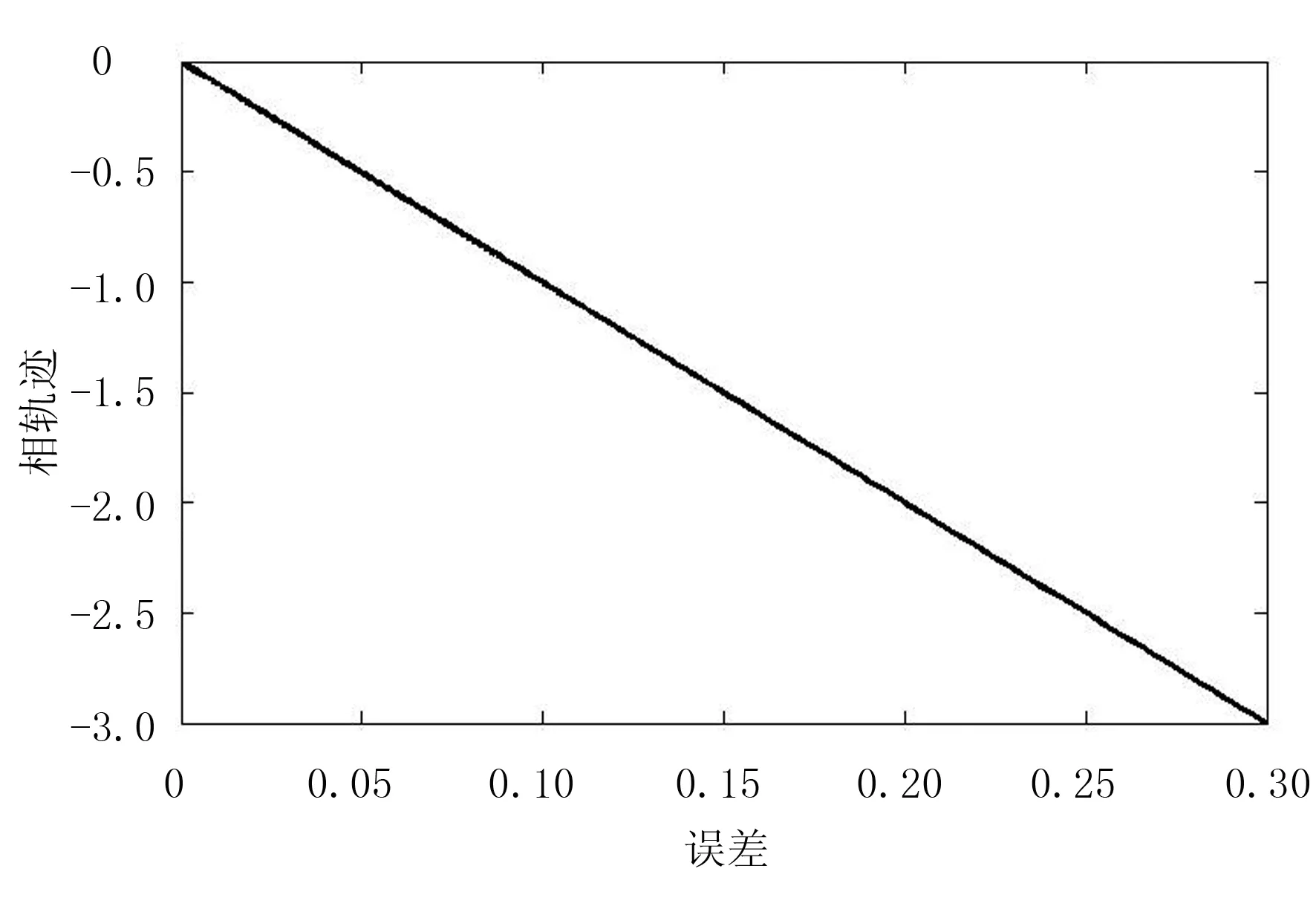
图7 本文算法相轨迹

5 结论

为有效地解决劳动力不足、提高果蔬采摘的质量、降低采摘成本，设计了一种草莓采摘机器人。考虑到草莓采摘机器人各关节均采用电机驱动，伺服系统中存在的非线性、扰动及不精确建模都会影响到其控制的品质，提出了利用滑模控制来控制草莓采摘机器人的各关节伺服电机，并对滑模控制进行改进以抑制其系统中存在的抖动现象。为了验证其有效性，在MatLab中对其进行仿真，仿真结果表明：所设计的控制算法具有良好的抗外部干扰能力和位置跟踪能力；改进后的滑模控制进一步抑制了指数趋近律滑模控制中存在的抖动现象，提高了系统的性能，减少了系统被破坏的概率。

[1] 宋健，张铁中，徐丽明，等．果蔬采摘机器人研究进展与展望[J].农业机械学报，2006，37(5) :158-162．

[2] 陈磊，陈帝伊，马孝义．果蔬采摘机器人的研究[J].农机化研究，2011，33(1) :224-231．

[3] Edan Y, Gaines E. Systems engineering of agricultural robot

design [J]. IEEE Transactions on Systems,Man, and Cybernatics, 1994,24(8): 1259-1265.

[4] Van Henten E J, Schenk E J. Van Willigenburg L G.,et al. Collision-free inverse kinematics of the redundant seven-link manipulator used in a cucumber picking robot[J].Biosystems Engineering, 2010,106 (2):112-124.

[5] 张洁,李艳文.果蔬采摘机器人的研究现状、问题及对策[J].机械设计,2010,27(6): 1-4.

[6] 冯青春，纪超，张俊雄，等．黄瓜采摘机械臂结构优化与运动分析[J].农业机械学报，2010，41( S1) : 244-248．

[7] 李伟，李吉，张俊雄，等．苹果采摘机器人机械臂优化设计及仿真[J].北京工业大学学报，2009， 35( 6) : 721-726．

[8] 唐志国，李元春，姜日花.机械臂协调操作柔性负载自适应模糊滑模控制[J].吉林大学学报：工学版，2011，41(2):484-490．

[9] 陈辛． 机械臂的动力学研究[D].哈尔滨: 哈尔滨工程大学，2007．

[10] Z M C,J G Z,Z Y W.Sliding Mode Control of Manipulator Based on Neural Network Reaching Law[C]//IEEE International Conference on Control and Automation，2008:370-373.

[11] Z M C,W J M,J G Z.Fuzzy Reaching Law Sliding Mode Control of Robot Manipulators[J].Proceedings of 2008 Pacific-Asia Workshop on Computational Intelligence and Industrial Application，2008(2):393-397.

[12] Y Niu,D W C Ho,Z.Wang.Improved Sliding Mode Control for Discrete-Time Systems via Reaching Law[J].Control Theory&Applications,IET，2010，4(11):2245-2251.

[13] 毛亮亮,周凯,王旭东.永磁同步电机变指数趋近律滑模控制[J].电机与控制学报,2016(4):106-111.

[14] 于林科,郑建明.开关磁阻电机直驱电液位置伺服系统模糊滑模控制仿真[J].哈尔滨理工大学学报,2011,16(5):76-80.

[15] 陈雪飞,李红梅,王晓晨,等.基于自适应滑模观测的无速度传感器感应电机间接磁场定向滑模控制[J].微电机,2011,44(1):46-49,54.

[16] 于双和,强文义,傅佩琛.无抖振离散准滑模控制[J].控制与决策,2001,16(3):380-382.

[17] 陈福红,马大为,乐贵高,等.火箭炮交流伺服系统动态滑模控制[J].南京理工大学学报：自然科学版,2012,36(4): 612-617.

[18] 高雅,刘卫国.基于卡尔曼滤波的永磁同步电动机滑模控制[J].微特电机,2011,39(6):41-43,47.

[19] 金宁治,张忠民,刘端增.具有增益调度切换增益的永磁同步电机滑模控制[J].电气传动,2015,45(4):3-7.Abstract ID:1003-188X(2017)07-0214-EA

Adaptive Sliding Mode Control Law for Picking Joint Eobot

Yuan Yuxia， Zhu Xiaohui

(Zhengzhou Science College, Zhengzhou 450064, China)

Using the discrete reaching law to design the sliding mode control can effectively reduce chattering phenomenon of the sliding mode control, but the effects of chattering inhibition has close relation with the sampling time and the discrete reaching law parameters. In this paper, an adaptive sliding mode controller was proposed based on the chattering analyzing of the exponential reaching law, this controller can further inhibit the chattering sliding mode controller with reaching law. In order to verify the effectiveness of the proposed method in this paper, the algorithm has been realized in the MATLAB platform, and it was used to control the harvesting robot, the simulation results show that the proposed algorithm has good position tracking ability, and the chattering phenomenon existing in the sliding mode control has been reduced, and the performance of the system has been improved.

discrete reaching law; adaptive sliding mode; harvesting robot; position tracking； Chattering

2016-05-29

河南省科技攻关计划项目(152102210002)

袁玉霞(1982-)，女，河南开封人，讲师，硕士，(E-mail) yuanyx1982@126.com。

朱小会(1982-),女，河南周口人，讲师,硕士，(E-mail) zhxh1983@yeah.net。

S225;TP242

A

1003-188X(2017)07-0214-04