沙棘果实-果柄系统振动采收机理分析与仿真
彭 俊,孙世鹏,冯亚利,杨有刚,傅隆生
(西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100)
沙棘果实-果柄系统振动采收机理分析与仿真
彭 俊,孙世鹏,冯亚利,杨有刚,傅隆生
(西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100)
沙棘在西部广泛种植,用于水土保持和防风固沙。其果实营养丰富、有较高经济价值,但采收非常困难,影响其经济价值。为改变人工采摘的状况,有必要进行沙棘的机械化采收研究。为此,研究了沙棘果实与果柄脱离的振动采摘机理,建立了双自由度受迫振动物理模型,推导出动力学方程,并采用数理微分方程求解得到沙棘果实-果柄系统稳态受迫振动输出解及采摘惯性力。同时,通过贝塞尔函数曲线模拟果实的几何形状,得出果实几何轮廓曲线方程,并利用Pro/E的函数功能画出沙棘果实的三维模型,将模型导入有限元分析软件ANSYS进行了模态分析。结果表明:理论计算的果实-果柄系统的位移、速度和加速度响应与有限元仿真分析的结果比较相符,频率在18~46Hz范围内时,果实部分产生共振且主振型最大,故果实的最佳采摘频率范围可确定为18~46Hz。该研究为沙棘振动采摘装备的开发提供理论基础。
果实-果柄;振动采收;有限元方法;模态分析
0 引言
沙棘(sea buckthorn)属胡颓子沙棘属,为落叶灌木,其果实为浆果。沙棘是优良的水土保持树种,因此在中国西部被广泛的种植,面积约为266.7hm2,占到世界沙棘资源储量的95%以上。沙棘果实富含维生素和酚类化合物,在世界上的某些地区作为药材和食品[1-2];但沙棘果小、柄短,且树枝有刺,难以采收。在加拿大,收获4hm2的沙棘所需的劳动力成本占生产总成本的58%。在亚洲,收获仍主要依靠手工或使用简单的手持工具,需要大约1 500工时/hm2[3]。因此,机械或其他沙棘果实收获技术的发展已经引起了相当大的关注。
果树的机械特性随着树种、品种和树的几何结构的变化而差异很大,但果实-果柄结构的机械特性变化不是很明显[4],故本文将沙棘果实-果柄作为沙棘树的一个基础系统来研究其振动采摘机理,为沙棘的机械振动采收提供一定的理论基础。
1 沙棘果实果柄系统振动机理研究
1.1 果树系统建模
为了解果树结构在振动激励下的动态响应,Savary等建立了柑橘的主干侧枝有限元模型,分析了模型在冲击激励下的加速度值。其仿真结果与实验结果比较吻合,两种方法得出的数据都表明了同一结论:激振频率越高,果树的加速度越大[5]。Láng建立了基于树干-主根的单自由度结构模型,研究表明:当振动位置靠近根部时,旋转式偏心振子激振器更有效,而激励作用点靠近树枝时,曲柄滑块式激振器更有效[6]。Upadhyaya等将树叶和树干上的小枝忽略,把主干分成许多个近似均匀的单元,采用Timoshenko梁理论进行计算,所得结果与测试结果比较接近[7]。Yung和Fridley将果树简化为由树干-树枝、树枝-树叶、果实-果柄3种具有不同力学特性的单元构成,并利用有限元方法分别对3种单元体的动力学模型进行了模拟,模拟分析结果与计算结果一致[8]。
1.2 果实-果柄系统采摘条件及受力模型建立
在振动过程中,当振动使果实产生的惯性力大于果实-果柄的连结力时,果实才能脱离下来。因此,可以将果实-果柄结构作为树的一个基础系统来研究,以确定最佳的振动频率和收获成熟果实的效率。当振动激励作用于树枝时,树枝和果实做强迫振动,振动响应X(t)为瞬态响应和稳态响应之和,即
X(t)=xT(t)+xS(t)
(1)
其中,xT(t)为沙棘树枝果实的瞬态响应;xS(t)为沙棘树枝果实的稳态响应。
由式(1)得受迫振动沙棘果实所受惯性力F(t)为
(2)
其中,m2为沙棘果实的质量。由于瞬态振动xT(t)是衰减振动,只在振动开始的很短时间内才有效,一般情况都不考虑[10],主要研究输出稳态响应xS(t)下的惯性力。若果实与树枝的连结力为F0,则实现振动采摘的条件为:振动产生的惯性力F(t)≥F0。以果实和树枝为研究对象,建立沙棘树枝果实的几何模型与力学模型,求解振动采摘过程中果实的动态响应,如图1所示。
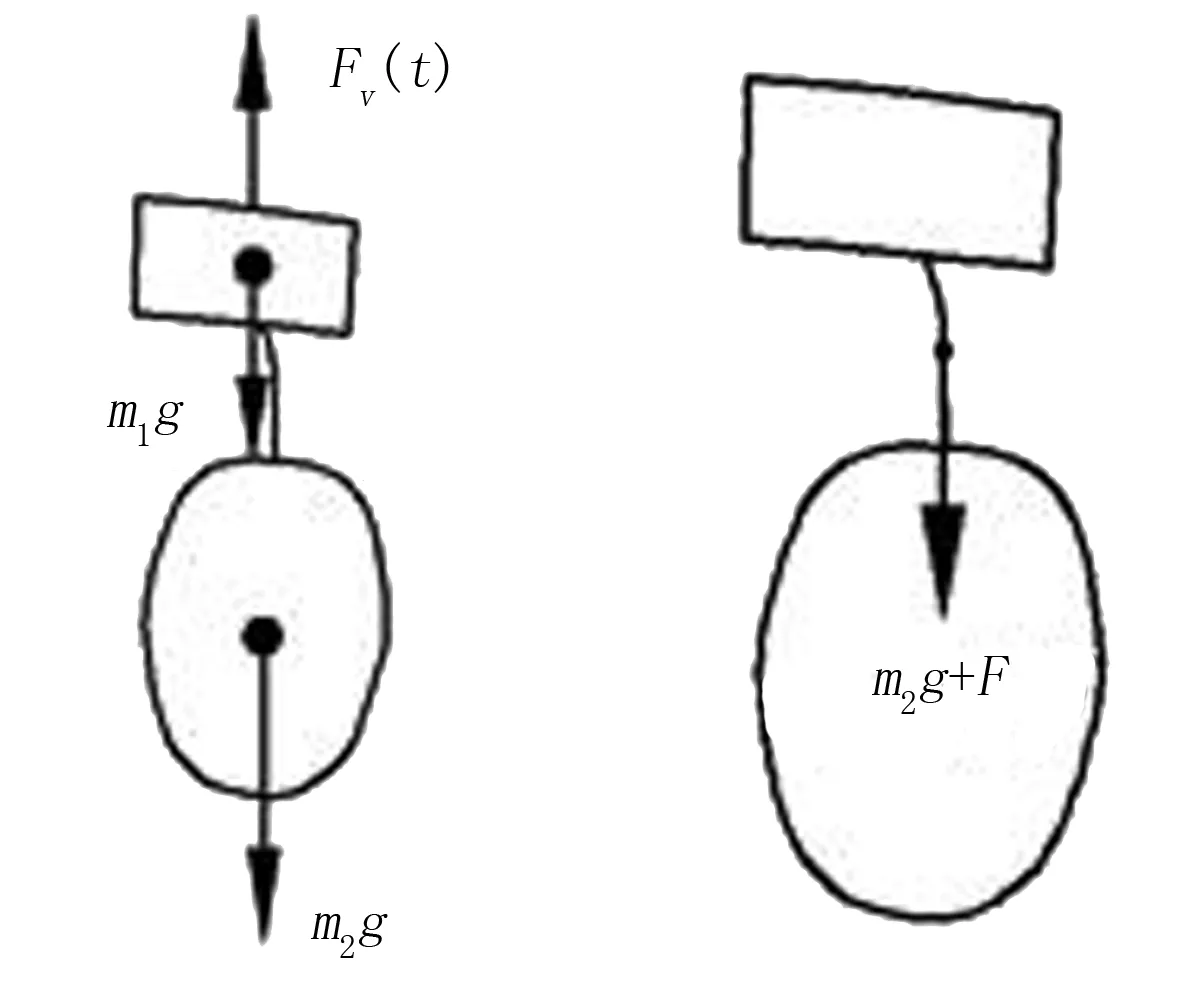
(a)
(b)
1.3 果实-果柄系统振动物理模型建立与求解
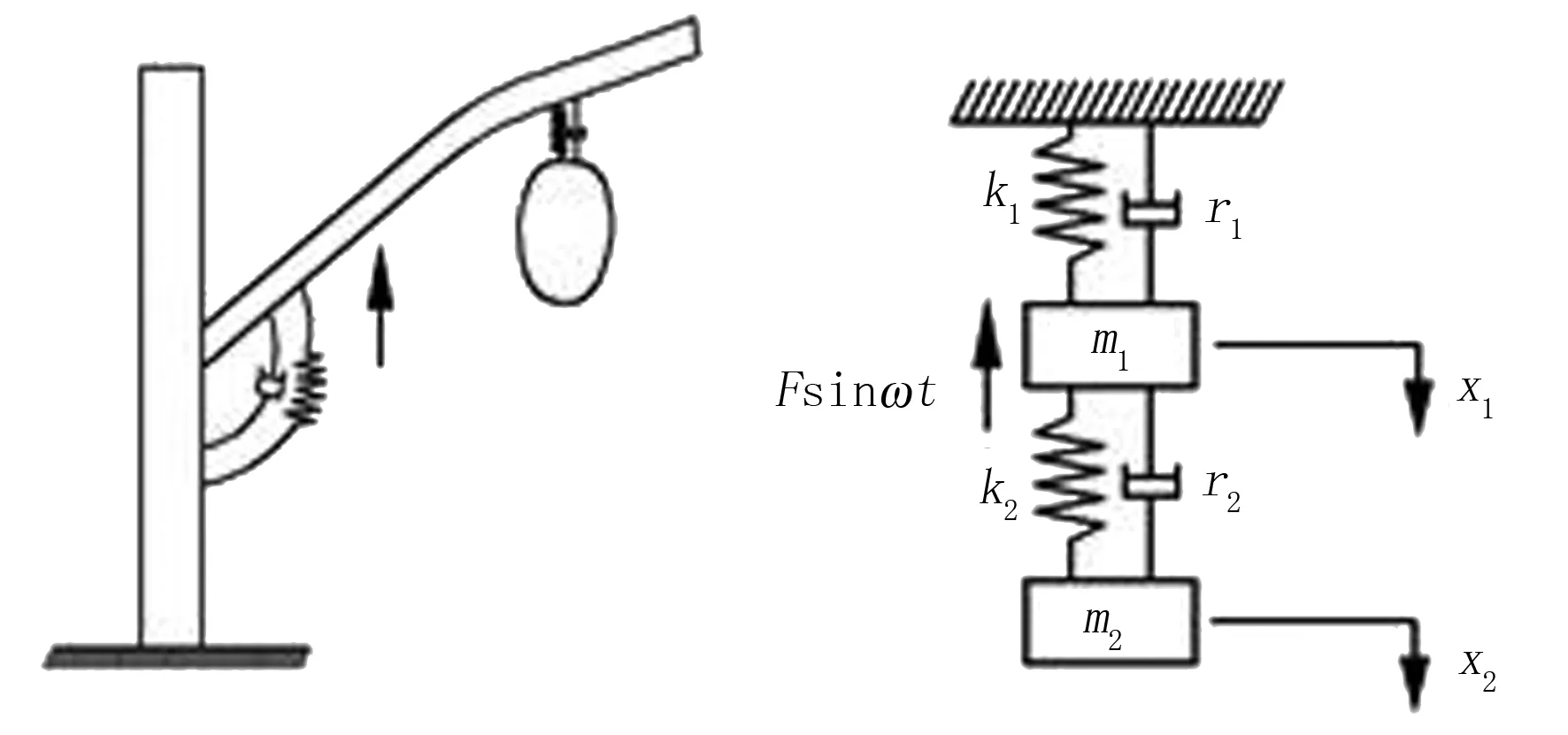
当沙棘树枝受到采摘激振力Fsinωt时,树枝整体会产生振动响应,沿树枝方向每个单位长度的树枝在振动响应下都会产生惯性力F(t)。沙棘的果柄很短,直径也很小,故其质量相对于树枝和果实的质量可以忽略不计。根据振动理论,可以将树枝果实系统看作二自由度的弹簧质量块振动系统,如图2所示。系统振动微分方程为
(K1+K2)x1-K2x2=Fsinωt
(3)
(4)
其中,x1、x2分别为树枝的位移和果实的位移;K1、K2分别是树枝和果柄的等效刚度。
树枝振动时,可将其看作是与主干连接处为固定端的悬臂梁,当受到外力时发生弯曲变形,树枝弯曲等效刚度K1,果柄可以近似为圆柱体,其等效拉伸刚度K2,则有
K1=3EJ/L13,K2=EA/L2
(5)
其中,E为材料弹性模量;J为截面惯性矩;L1为树枝长度;A为果柄截面积;L2为果柄长度。
其受迫振动的位移响应为
x1=A1ei(ωt-φ),x2=A2ei(ωt-φ)
(6)
其中,A1、A2分别为树枝的位移和果实的位移的振幅。将式(6)代入得
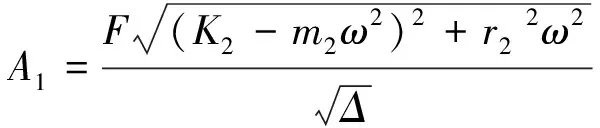
(7)
Δ=[K1K2+
(m1m2ω4-r1r2ω2-K1m2ω2-K2m1ω2-K2m2ω2)]2+
(K1r2ω-m2r1ω3-m2r2ω3-m1r2ω3+K2r1ω)2
(8)
由于系统的阻尼对系统固有频率的影响很小,故系统的固有频率可表示为
(9)
2 果实果柄系统有限元分析
2.1 果实树枝物理参数测定
J. Khazaei等[11]研究了不同温度和载荷对沙棘果实的机械特性及应力松弛的影响。对浆果进行了穿刺实验,对不同温度下的大果沙棘的密度、弹性模量及泊松比进行了测试。树枝样本取材于新疆青河县大果沙棘良种基地,密度用排水法测量。
尚大军等对沙棘木材的力学性能进行了测定,实验结果表明:应力波测得未经处理的中国沙棘木材弹性模量与超声波测得结果相差不大[12]。张厚江等用两点悬挂振动测定了木材的动态弹性模量[13]。刘镇波等采用基于打击音的快速傅里叶变换(FFT)频谱分析法测量了木材弹性模量[14]。贺磊盈在研究山核桃树枝干的结构参数时,采用了悬臂梁振动实验测得树枝的动态弹性模量[15]。动态弹性模量为
(10)
由于木材粘弹性的存在,振动过程中不可避免地存在阻力,因而在一定时间内振动会逐渐衰减而停止。阻尼的种类很多,通常都以粘性阻尼为基本模型来分析有阻尼的振动,对于非粘性阻尼可以引进等效粘性阻尼来近似计算[16-17]。陈守谦用衰减振动法对木材的阻尼比进行了测定,通过测得木材自由衰减振动的对数衰减率δ,再通过阻尼比ζ与δ的关系求出阻尼比[18-19]。阻尼比ζ与对数衰减率δ的关系式为
(11)
其中,A1和A1+N分别表示振动信号的第1个波峰幅值和第1+N个波峰幅值。
采用悬臂梁振动实验,实验材料包括:沙棘树枝,固定树枝的虎钳,施加激励的激振锤(京仪北方测振仪器分公司,LC-1),加速度计(KYOWA公司的AS-2GB)。将树枝加工成圆柱形,用虎钳夹住一端并安装加速度计,另一端用激振锤敲击,记录树枝振动的加速度。对振动加速度信号进行快速傅里叶变换(FFT),提取1阶共振频率信号,如图2所示。实验测得树枝具体参数如表1所示。
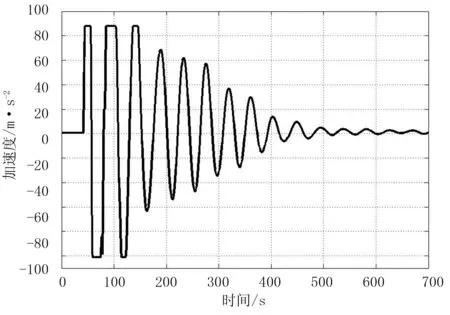
(a) 振动加速度时域响应

(b) 振动加速度频域响应
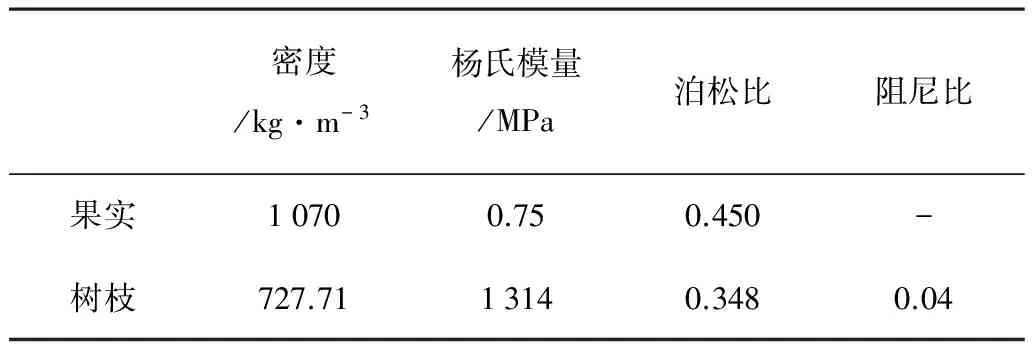
密度/kg·m-3杨氏模量/MPa泊松比阻尼比果实10700.750.450-树枝727.7113140.3480.04
2.2 果实几何模型的建立
沙棘果实近似为椭圆形状,为了建立精确的果实几何模型,用贝塞尔曲线来模拟果实的轮廓。贝塞尔曲线法是建立曲线特征多边形,只要移动多边形顶点的位置,就能够方便地改变曲线的形状,使曲线很快收敛于要求的形状[20]。它通过控制曲线上的4个点来编辑图形,所以能较为精准地模拟果实轮廓。贝塞尔曲线方程为
B(t)=p0(1-t)3+3p1t(1-t)2+
3p2t2(1-t)+p3,t∈[0,1]
(12)
其中,p0、p1、p2、p3分别为4个控制点的坐标。为了得出果实轮廓的曲线方程,先将沙棘果实图片导入软件AutoCAD中,用样条曲线控制点方式模拟外轮廓得出曲线的12个控制点坐标,然后把坐标代入方程(12)得到每段轮廓曲线的函数方程。运用三维建模软件Pro/E的函数功能创建已知轮廓曲线的三维果实模型,沙棘果实样本来自新疆青河县林管站国家大果沙棘良种基地,品种为俄罗斯大果沙棘“楚依”。选取了20个果实样本,其中3个样本的三维模型图如图3(a)所示。

(a) (b)
2.3 果实果柄系统模态分析
模态分析是研究结构动力特性一种近代方法,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析[21]。模态分析的目的是描述系统的动态特性,在时域里,系统的模态参数是独立于外部条件的。
为了更加真实地模拟果实果柄系统,将果实和果柄分割为两个实体,再用不同的材料划分网格,第1个果实模型的网格划分与约束如图3(b)所示。模态分析采用Block Lanczos法,在树枝下端施加了零位移约束。此有限元模型由23 453个单元和5 032个节点组成的多自由度结构,所以其有多个固有频率和模态振型。而在振动采收时频率太高会造成树体的损伤,故提取了前6阶低阶固有频率。
3 结果与分析
3.1 模态振型图分析
振型是指体系的一种固有的特性,与固有频率相对应。每一阶固有频率都对应一种振型。振型对应于频率而言,一个固有频率对应于一个振型,其中前6阶模态振型图如图4所示。沙棘果实脱落一般是从果柄与树枝的连接处脱落,所以振动能量主要集中在果柄区域或果实上部,才有可能使果实脱落。由以上模态振型图可以看出:第3阶模态的变形能量主要集中在果实中间的大部分区域,第4阶和第5阶模态振型图的变形能量主要集中在果实的上部,而其余阶模态都集中在离果柄比较远的区域,故第3~5阶频率被作为振动收获的可行性区域。
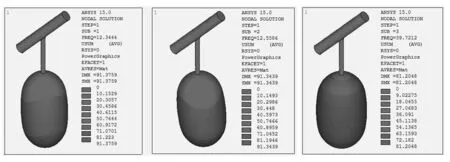
(a) 第1阶 (12.34Hz) (b) 第2阶 (12.56Hz) (e) 第3阶 (39.72Hz)

(f) 第4阶 (246.79Hz) (g) 第5阶 (299.02Hz) (h) 第6阶 (300.30Hz)
3.2 系统固有频率回归分析
20个样本模型的固有频率如表2所示。从表2可以看出:每个样本的固有频率都不一样,因为每个果实几何结构都不一样。果实几何参数主要有果柄长度、果柄直径及果实体积。为了寻找果实频率与果实体积、果柄长度、果柄直径之间的关系,为以后进一步分析提供预测,建立回归模型。
设系统固有频率为y,果实长度为x1,果柄直径为x2,果柄直体积x3,分别建立第3~5阶频率的三元回归模型如下:
第3阶y3=10.04+1.09x1+51.67x2-0.03x3
第4阶y4=202.85+3.11x1+121.05x2-0.16x3
第5阶y5=220.77-18.59x1+336.88x2-0.17x3

表2 果实样本模型尺寸参数与固有频率回归模型误差分析表
由表2可以得出:第3阶、第4阶、第5阶固有频率的计算值和回归模型获得的值都相差不大,相互之间没有显著性差异,且回归模型获得的值与计算值的平均绝对百分误差也比较小;第3阶回归模型的百分误差相对较大为8.62%,其他两阶模型的误差都在3%左右。
4 结论
分析果实-果柄系统的受迫振动稳态解可知:果实的振动幅度随着树枝所受的采摘惯性力和采摘频率的增大而增大,树枝的振动幅度随着果实质量的增加而减小。结合有限元模态分析得出的振型图可知:在第3阶共振频率时,果实整体的振动幅度最大;在第4阶和第5阶共振频率时,果实靠近果柄处的振动幅度比较大,但其对应的频率比较高而不适合机械收获。因此,在实际收获中可选择第3阶频率。
以果柄长度、果柄直径及果实体积为变量的回归模型的平均绝对百分误差都在9%以内,因此对于不同几何参数的果实均可通过此回归模型初步预测果实果柄系统的固有频率。
[1] 宋自娟,徐怀德,高锦明,等.加工过程中冷打浆沙棘浓缩浊汁理化特性的变化[J].农业工程学报,2014,30(3):264-270.
[2] L M Bal, V Meda, S Naik, et al. Sea buckthorn berries:A potential source of valuable nutrients for nutraceuticals and cosmoceuticals[J].Food Research International, 2011, 44(7):1718-1727.
[3] 梁建平,慕后春,杨浩生.沙棘果实采收技术及装备现状分析[J].沙棘,2008,21(4):17-20.
[4] H A Tinoco, D A Ocampo, F M Pea, et al.Finite element modal analysis of the fruit-peduncle of Coffea arabica L. var. Colombia estimating its geometrical and mechanical properties[J]. Computers and Electronics[J]. Agriculture, 2014,108: 17-27.
[5] S K J U Savary, R Ehsani, J K Schueller, et al. Simulation study of citrus tree canopy motion[J].Transac.ASABE, 2010, 53(5): 1373-1381.
[6] Z Láng.A one degree of freedom damped fruit tree model[J].Transactions of the ASABE, 2008, 51(3):823-829.
[7] S K Upadhyaya, J R Cooke, R H Rand. Limb Impact Harvesting, Part I: Finite Element Analysis[J].Transactions of ASAE, 1981, 24(4): 856-863.
[8] R Fridley, C Yung. Computer analysis of fruit detachment during tree shaking[J].Transactions of the ASAE, 1975, 18(3):409-415.
[9] 李有堂.机械振动理论与应用[M].北京:科学出版社,2012.
[10] J Khazaei, D D Mann. Effects of Temperature and Loading Characteristics on Mechanical and Stress Relaxation Properties of Sea Buckthorn Berries. Part 2. Compression Tests[J].Agricultural Engineering International: CIGR Journal, 2004.
[11] 尚大军,段新芳,杨中平,等.两种无损检测方法对CCA处理材的性能评价比较[J].木材工业,2008,22(2): 17-19.
[12] 张厚江,申世杰,崔英颖,等.振动方式测定木材弹性模量[J].北京林业大学学报,2005(6):91-94.
[13] 刘镇波,刘一星,于海鹏,等.实木板材的动态弹性模量检测[J].林业科学,2005(6):129-134.
[14] 贺磊盈.面向振动采收的果树枝干三维重建方法及其动力学特性研究[J].杭州:浙江理工大学,2014.
[15] 清华大学固体力学教研组.机械振动[M].北京:机械工业出版社,1980.
[16] 阮锡根,余观夏.木材物理学[M].北京:中国林业出版社,2005.
[17] 陈守谦.用衰减振动法测定木材的阻尼参数[J].林业科技,1990(4):31-33.
[18] 陈守谦,张晓兵.受迫振动时木材阻尼参数的研究[J].林业科技,1992(2):36-38.
[19] 张祖媛.贝塞尔曲线的几何构型[J].四川工业学院学报,1998(4):33-36,45.
[20] X Tang, J Ren,C Liu, et al, Simulation of Vibration Harvesting Mechanism for Wolfberry, ASABE Annual International Meeting[C]//2011 Louisville Kentucky USA,2011.
Mechanism Analysis and Simulation of Vibration Harvesting of the Sea Buckthorn Fruit-stalk System
Peng Jun, Sun Shipeng, Feng Yali, Yang Yougang, Fu Longsheng
(College of Mechanical and Electronic Engineering, Northwest A&F University, Yangling 712100 China)
Sea buckthorn is an ideal plant for ecological management and was thus planted widely in the western of China. Its fruit is rich in nutrition, and has high economic value, but sea buckthorn fruit is very difficult to be harvested. In order to change the situation mainly by manual picking, it is necessary to study the mechanized harvesting of sea buckthorn. In this paper, the mechanism of fruit-stalk detachment by vibration was studied, and a two degree of freedom forced vibration physical model is established and derive the kinetic equation. The steady forced vibration solution and the inertia detachment force of the fruit-stalk system were obtained by solving mathematical differential equations. Meanwhile, the geometric outline of fruit, of fruit is simulated by Bessel's function curve, and the geometric curve equation of the fruit were used to draw the 3D model of the fruit in Pro/E. Afterwards, the fruit model was introduced into the finite element analysis software ANSYS to carry out Modal analysis. The results show that the displacement, velocity and acceleration of the fruit-stalk system were in conformity with the results of finite element simulation analysis. When the frequency is in the range of 18~46Hz, the part of the fruit is resonant and the main mode is the largest. This will provide the theoretical basis for the development of the vibration picking equipment for sea buckthorn fruit.
fruit-stalk; vibration harvest; finite element; model analysis
2007-06-07
国家自然科学基金项目(31301242);中国博士后科学基金项目(2015M572602);陕西省自然科学基础研究计划-青年人才项目(2015JQ3065);教育部留学归国人员科研启动基金项目(K308021401)
彭 俊(1991-),男,陕西安康人,硕士研究生,(E-mail)jxpengjun@nwsuaf.edu.cn。
傅隆生(1984-),男,江西吉安人,副教授,博士,硕士生导师,(E-mail)fulsh@nwsuaf.edu.cn。
S225.93
A
1003-188X(2017)07-0028-06

