基于信号采样自相关的步进宽带频谱感知方法

2017-12-15 01:25伍小芹

数据采集与处理 2017年5期

关键词：检测时间虚警门限

陈露伍小芹白勇

(海南大学南海海洋资源利用国家重点实验室，海口，570228)

基于信号采样自相关的步进宽带频谱感知方法

陈露伍小芹白勇

(海南大学南海海洋资源利用国家重点实验室，海口，570228)

采用步进频域能量检测法可以提高在软件无线电平台的频谱感知的带宽范围，但能量检测法易受噪声不确定性的影响，而信号采样自相关检测法对噪声不确定性有很好的鲁棒性。为进一步提高软件无线电的检测性能，提出了基于信号采样自相关的步进宽带频谱感知方法。首先阐述了信号采样自相关检测的原理，然后对基于该原理的步进宽带检测方法的流程进行了分析，最后利用MATLAB软件仿真其检测性能。仿真结果表明，在信噪比(Signal-noise-ratio, SNR)不同的情况下，基于信号采样自相关的步进宽带频谱检测方法能达到所要求的检测性能。此外，为了兼顾频谱感知的检测速度和频带带宽分辨率之间的关系，进一步提出了在原本固定步进值的步进宽带信号采样自相关的频谱感知方法中采用可变步进值的两阶段检测方法，该方法可以获得较高的频带带宽检测分辨率和较短的检测时间。

软件无线电；频谱感知；采样自相关；信号检测；检测性能

引言

随着无线通信技术的不断发展，新兴的无线通信业务需要大量的频谱资源来支撑其发展。但是目前可分配使用的频谱资源却越来越稀少；再者，静态(固定)分配频谱的方式是当前大多数国家和地区都在采用的频谱管理模式，但该频谱管理方式会降低频谱资源的利用率。利用软件无线电(Software defined radio, SDR)和认知无线电(Cognitive radio, CR)技术可以在感知空闲频谱的基础上采用动态的频谱接入方式来充分利用空闲频谱资源，从而改善频谱资源紧缺和频谱利用率低的问题。

目前，主要的频谱检测算法包括能量检测法(Energy detect, ED)[1-3]、匹配滤波法(Matched-filtering)[4]、平稳循环法(Cyclo-stationary)[5]以及特征值法(Eigenvalue)[6]等。ED是由著名学者H.Urkowitz在1967年提出的信号检测算法，它不需要任何先验信息，并且检测时间短，是目前应用比较广泛的检测算法。但是，噪声的不确定性[7]直接影响了其性能。

新加坡学者Zeng和Liang等[8，9]提出利用统计协方差矩阵的特性进行信号检测可以克服噪声不确定性的影响。该方法利用授权主用户(Licensed primary user, PU)信号与白噪声这两者的自相关矩阵的不同特性，来判断PU信号是否存在。与特征值检测法不同，理论得出的检测门限值的表达式相对简单。同时，该算法能在信号、信道以及噪声等先验信息未知的情况下进行信号检测，是一种盲检测算法[10]。

文献[11]中提出可以利用多频带联合检测的方式来实现固定宽带频谱感知，但是只考虑了固定带宽的情况。而在实际的频谱检测中，设备的最大检测带宽小于需要检测的带宽时，设备不可能一次性就完成对全频段的检测，利用软件无线电平台(如 GNU radio)可实现宽带频谱感知功能。文献[12]中，作者提出的利用步进的方法来实现频域能量检测的宽带频谱感知法可以提高无线电系统的频谱感知的带宽范围。但是ED对噪声功率不确定性非常敏感，特别是信噪比较低时，其检测性能显著下降。

在前文分析讨论的基础上，为了进一步提高无线电系统在实际应用中的频谱检测性能，本文提出了基于信号采样自相关的步进宽带频谱检测算法，以避免噪声功率的不确定性对检测性能带来的严重影响。首先分析了基于信号采样自相关的频谱检测算法的原理和其宽带频谱感知的流程，然后利用MATLAB仿真软件仿真了信号采样自相关的步进宽带频谱检测算法的检测性能。结合仿真结果讨论了影响信号采样自相关检测的判决门限的相关因素，包括研究判决门限与检测性能(虚警概率和检测概率)以及相关影响因素(如平滑因子，信噪比和检测时间等)之间的关系。仿真结果表明，在信噪比不同的情况下，本文提出的算法能达到所要求的检测性能。另外，为了平衡检测时间(检测速度)和频带带宽分辨率之间的矛盾，提出了改变步进值的进宽带采样自相关的方法，由此改进原来的固定步进值的步进宽带信号采样自相关的检测算法，不仅可以获得较高的频带带宽分辨率，而且缩短了检测时间。

1 信号采样自相关检测算法

1.1 检测原理

信号采样自相关检测算法是一种基于广义似然比(Generalized likelihood ratio test，GLRT)准则的检测算法[13]，能产生一个与噪声功率无关的检验统计量来完成信号检测，因而对噪声功率的不确定性具有很好的鲁棒性。

一般由二元假设检验来建立频谱检测模型。在H0和H1两种假设检验下，接收信号采样后的表达式为

H0:y(n)=η(n)

(1)

H1:y(n)=s(n)+η(n)

(2)

式中：H0假设表示不存在PU信号；H1假设表示存在PU信号；x(n)为检测信号采样；η(n)为噪声采样；y(n)为接收信号采样；s(n)表示一个经过衰落与多径影响的无线传输后的信号采样；N代表总采样数(其检测时间为T);n=1,2,…,N。

从y(n)，s(n)和η(n)的离散采样序列可知，选择合适的矩阵长度L(平滑因子)进行连续的采样并定义为

式中:n=0,1,…,N-1；[·]T表示矩阵转置。定义自相关矩阵为

(6)

(7)

(8)

根据矩阵性质，可得

Ry=Rs+Rη

(9)

(10)

(2) H1假设下，s(t)≠0且信号采样自相关，那么矩阵Rs以及Ry中非对角线上的元素不全为0。实际中，由于观测样本数量有限，自相关矩阵只能通过一次观测样本来得到样本自相关矩阵Ry(Ns)，然后近似等于统计自相关矩阵Ry。选择合适的采样因子L，定义采样自相关矩阵Ry(Ns)为

(11)

式中:Ns为计算信号采样自相关系数时的个数，接收信号y(n)的采样自相关的表达式为

(12)

信号采样自相关矩阵是对称的Toeplitz矩阵。由上述分析可得，在H0和H1假设下，根据自相关矩阵中对角线元素和非对角线元素的不同特性，来判断主用户信号是否存在。因此，定义自相关矩阵中对角线元素和非对角线元素的比值为检验统计量，并与判决门限进行比较，来确定PU信号是否存在。定义rij为Ry(Ns)的元素，令γ为检测门限值，可得本文的采样自相关检测算法的检验统计量T为

(13)

(14)

T=Tall/Tdiag

(15)

由于λ(l)是Ns个随机变量的线性求和运算，根据中心极限定理，当Ns→∞时，λ(l)近似服从于高斯分布，则Tall和Tdiag也都近似于高斯分布，因此有

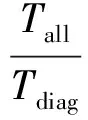
(16)

式中：[Tall(Ns)]和[Tdiag(Ns)]分别表示Ry矩阵经过一次Ns个采样点后得出的Tall和Tdiag。

该二元检测方法的表达式为：若T>γ，则主用户信号存在；否则，主用户信号不存在。信号采样自相关算法的成立隐含了一个先决条件：噪声总是独立不相关的，而接收信号具有相关性。在实际中，由于发射信号本身具有相关性以及信道存在多径效应等原因，接收信号总是有相关性的。此外，还可以通过过采样处理使得信号具有相关特性。

在实际通信环境中，噪声不确定性始终存在，它对能量检测算法的影响不能忽视，特别是在SNR较低时，能量检测算法的检测性能显著下降。而信号采样自相关检测算法不需要PU信号、噪声以及信道的先验信息，且对噪声不确定性有很好的鲁棒性，这就是信号采样自相关检测算法相比能量检测算法的优势所在。

1.2 检测门限确定的方法

在信号检测中，检测概率和虚警概率是衡量信号检测算法优劣最重要的指标。选取合理的门限值，可以使虚警概率最小和检测概率最大，因此，检测门限值的选取是提高算法检测性能的关键。文献[14]指出降低总的错判概率可以提高检测性能，文献[15]综合考虑检测概率和虚警概率，推导出基于最小错判概率判决准则的门限。本文将根据一定的虚警概率和检测概率来选取合适的判决门限值。在主用户检测中，检测门限一般可由两种方法来确定[10]。

(1)理论推导，通常依据Newman-Pearson准则来推导出虚警概率和检测门限之间的关系。

结合式(15)得出的检验统计量，在H0条件下，根据虚警概率的定义可得

Pfa=P(Tall/Tdiag>γ|H0)

(17)

[8，9]，可得出H0假设下的均值E[Tall(Ns)]和E[Tdiag(Ns)]之比为

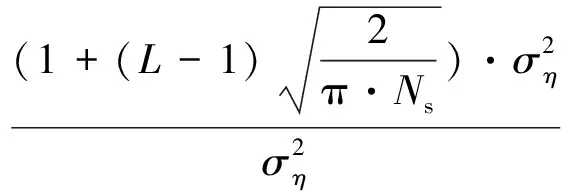
(18)

(19)

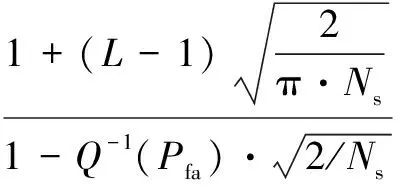
(20)

在Newman-Pearson准则下，根据预先设定的虚警概率值得到检测门限值。值得注意的是，上述的理论门限公式的推导是在接收信号不经过滤波器处理的前提下得出的。若是信号需要经过滤波器处理，该理论门限公式将无法适用[16]。

(2)实验仿真，即根据一定检测性能的要求，通过实验仿真来确定检测门限值。

上述理论门限公式是新加坡学者Zeng和Liang推导得出的，但推导过程中作了假设和简化，其门限并不能反映设定的虚警概率。同时，由于检测概率对检测门限的选取同样重要，若只是单纯依靠虚警概率来确定门限值是不全面的。除此之外，式(20)的理论门限值在经过一个接收滤波器之后，该理论门限值就无法适用。而本文提出的基于信号采样自相关的步进宽带检测算法，需要经过滤波器处理来得到步进检测信号，因此上述公式不适用。本文将通过分析影响判决门限的相关因素，结合实验仿真，依据一定的检测概率和虚警概率要求合理地选取判决门限，使得检测概率尽可能大，虚警概率尽可能小，从而达到提高检测性能的目的。

根据802.22协议草案中的标准，规定Pfa=0.01～0.1，Pd=0.9～1.0。在一定的检测概率和虚警概率的要求下，合理地选取判决门限值。预先设定Pd≥0.9和Pfa≤0.1。首先，信号源采用带宽为2 MHz的sinc基带信号进行BPSK调制，信号周期为0.5 μs；调制到中心频率为6 MHz和16 MHz的频带上。总的频谱检测范围为20 MHz,采样频率为40 MHz。假设噪声为高斯白噪声(均值为0，方差为1)。本文采用通带频率为200 kHz和阶数为500的Kaiser窗设置带通滤波器。仿真中信噪比不同时，噪声功率保持不变，改变信号功率，接收码元个数N=2 000，最后得到带宽为200 kHz的单个窄带信号采样自相关检测的门限值。

在平滑因子L分别为7和10的情况下，检测概率和判决门限的关系如图1所示。随着信噪比从-5 dB逐渐增大到5 dB，为了满足检测概率Pd≥0.95，当平滑因子L=7时，所需的检测门限最小值从8.5增大到8.7；当L=10时，所需的检测门限最小值从10.3增大到10.5。

在平滑因子L分别为7和10的情况下，检测门限与虚警概率的关系如图2显示。为了满足虚警概率Pfa≤0.05，当L=7时，所需的检测门限最大值从6.7增大到7.0；当L=10时，检测门限最大值从8.5增大到8.6。

图1 不同平滑因子L下检测门限与检测概率的关系(Ns=20 000) 图2 不同平滑因子L下检测门限与虚警概率的关系(Ns=20 000)Fig.1 Detection probability versus decision threshold with different L(Ns=20 000) Fig.2 False-alarm probability versus decision threshold with different L(Ns=20 000)

结合图1和图2的仿真结果可知，当平滑因子相同时，随着信噪比从-5 dB增大到5 dB，所需的检测门限值增大0.2左右，变化不大。本文主要考虑采样因子L不同时，满足Pd≥0.95以及Pfa≤0.05时的检测性能来共同确定可选门限值。根据实际需要在该区间内任意选择一个门限值与检验统计量进行比较，来完成信号检测的任务。具体推导过程为：在L=7的情况下，当Pd≥0.95时，需要的检测门限约小于8.5；当Pfa≤0.05时，需要的检测门限约大于7.0。因此，在L=7时，选取区间(7.0, 8.5)中的任一值作为此时的判决门限值均可满足Pd≥0.95和Pfa≤0.05的要求。在L=10的情况下，当Pd≥0.95时，需要的检测门限约小于10.3；当Pfa≤0.05时，需要的检测门限约大于8.6。因此，在L=10时，选取区间(8.6,10.3)中的任一值作为此时的检测门限值，均可满足Pd≥0.95和Pfa≤0.05的性能要求。

2 基于信号采样自相关检测的步进宽带频谱感知算法流程

在宽带频谱检测模型中，首先进行符合采样定理的时域连续采样，然后采样信号经过带通滤波器得到窄带采样信号，再进行信号采样自相关检测，得出该窄带内是否存在PU信号的检测结果。上述过程可看成是一单独的子带检测过程。对于宽带检测，本文采用多子带的逐个判决方式，即每段窄带进行采样自相关检测后，计算检测统计量与检测门限值比较，判断此窄带内主用户信号是否存在；再通过连续多个窄带检测直到整个宽带全部被检测完；最后，综合所有判决结果得到占用频谱和空闲频谱的准确范围。

在信号采样自相关的宽带频谱检测中，对每一步进的窄带信号的判决都是一个二元假设检验问题。假设连续采样的次数为n，则宽带频谱检测的检测统计量Tn可表示为

(21)

图3 基于信号采样自相关的步进宽带频谱感知方法流程Fig.3 Procedure of step-by-step wideband spectrum sensing based on signal sample autocorrelation detection

软件无线电平台(如GNU radio)可实现宽带频谱感知功能。当系统需要检测的频带范围大于设备的最大检测带宽时，可采用连续多次的步进方法来进行窄带检测，并对步进检测结果进行综合统计，从而实现大范围的宽带频谱感知[16]。本文采用带通滤波器来实现步进宽带的检测过程，通过多次改变带通滤波器的中心频率来实现多次步进的窄频带检测，算法步骤为：(1)设置初始参数如第一次单步检测的频段、整个宽带检测范围和相对较大的步进值等；(2)进行单步信号采样自相关检测，经过采样、滤波后选择合适的矩阵长度L，得到接收信号自相关矩阵；(3)计算统计检验量T，并与检测门限进行比较，得出判决结果。如果检验统计量大于判决门限，则可判断该频谱没有PU信号存在；(4)最后判断该频段是否超出宽带检测范围，若没有，则进入下一个检测频带，回到单步信号采样自相关检测，进入循环判决。直到超出设置的宽带检测范围时感知结束。软件无线电设备通过多次步进方法实现宽带检测的流程图如图3所示(不包括虚线框的内容)。

在采用步进原理的频谱检测算法中，检测时间(检测速度)和频带带宽分辨率之间相互制约，它们都受到选定的步进值大小的影响。若选定的单个步进值越小(如200 kHz，400 kHz)，频带带宽分辨率也会增加，但检测时间增多；若采用相对较大的步进值(如1 MHz，2 MHz)则会减少检测时间，但会降低频带带宽分辨率。原有的检测算法采用单一固定的步进值，难以平衡检测时间和频带带宽分辨率之间的矛盾关系。因此，本文在原来固定步进值的步进宽带频谱检测算法的基础上，提出改变步进值的步进宽带频谱检测算法。该检测方法如图3所示(包括虚线框的内容)。其检测步骤为：(1)设置参数如第一次单步检测的频段、宽带频谱检测范围和相对较大的步进值(如2 MHz)；(2)进行单步窄带信号采样自相关检测，得到检验统计量，并与检测门限进行比较：如果检验统计量T小于检测门限值，可判断此窄带空闲；如果T大于检测门限值，则可判断此步进的窄带被PU信号占用；(3)对于占用频带，采用相对较小的步进值在此频段内进行连续多次的单步信号采样自相关检测，直到检测完整个宽带频谱的范围。改进的算法改善了原有算法的宽带检测性能，缓解了检测时间与频带带宽分辨率之间的矛盾关系，适应性更广。

3 仿真与分析

以软件无线电平台GNU radio的参数为例，利用MATLAB软件来仿真步进宽带信号采样自相关检测的算法。

首先，产生BPSK调制信号来模拟接收信号(与1.2节中的参数相同)。采用带宽为2 MHz的sinc基带信号(信号周期为0.5 μs)，再调制到中心频率为6 MHz和16 MHz的频带上。调制后的信号所占频谱是5～7 MHz和15～17 MHz。总的频谱检测范围为20 MHz，采样频率为40 MHz。同样假设噪声为高斯白噪声(均值为0，方差为1)。最后，采用带通滤波器来实现步进方法的宽带检测过程。采用阶数为500、通带频率为200 kHz的kaiser窗来设置带通滤波器，接收码元个数N=20 00。Ns=40 000。步进值设置为200 kHz，通过多次改变带通滤波器的中心频率来实现步进方法的宽带采样自相关检测。需要得到每个200 kHz的窄带采样自相关检测的门限值。在本文的仿真中，信噪比不同时，噪声功率不变，只改变信号功率。

表1 不同采样因子下的可选门限值

由图1和图2可知，选择不同的检测门限对检测性能(Pd和Pfa)是有影响的。同时，在信噪比一定的情况下，为达到一定检测性能的要求，门限值随着采样因子L的增大而变大。SNR对检测门限的选取有一定的影响，但在本文中影响不大。在单次步进200 kHz的窄带信号采样自相关检测中，在同一L下，满足Pd≥0.95以及Pfa≤0.05的条件下，当信噪比从-5 dB增大至5 dB时，可跟据图1和图2的仿真结果来选择门限值，如表1所示。

图4为L=7的情况下SNR=5 dB的检测整个宽带为20 MHz的频谱检测图(单个窄带的检测带宽为200 kHz，执行100次)。依据以上分析，选取8.0做为检测门限。由图4可知，在20 MHz的宽带检测范围内，检验统计量T的值连续大于选定的门限值8.0的为5～7 MHz和15～17 MHz这两段频谱，这两段频谱均存在PU信号，其余的是不存在PU信号的空白频段。

图5给出了L=10的情况下SNR=-5 dB时检测整个宽带为20 MHz频谱检测图(需要执行100次的单个窄带为200 kHz的信号检测)。选取9.0做为检测门限，由图5可知，检验统计量T连续大于选定的门限值9.0的为5～7 MHz和15～17 MHz两处频段，这两段频谱均被PU信号占用；其余的频段都不存在PU信号，属于空闲频谱。

从信号采样自相关矩阵的公式可以看出，决定采样自相关矩阵的主要因素有L和Ns。在Ns不变的情况下，随着L的增加，采样自相关矩阵的阶数也随之增加，而检测概率则随着采样自相关矩阵的阶数的增大而增大，如图2所示。平滑因子在一定程度上决定了该算法的复杂程度。在满足一定检测性能的实际检测条件下，应该选择一个相对较小的L来减少算法的复杂度，本文仿真中选择L≤20。

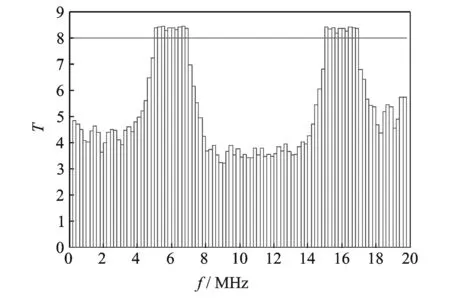
图4 基于信号采样自相关的步进宽带频谱检测图(SNR=5 dB，L=7)Fig.4 Detected diagram of step-by-step wideband spectrum sensing based on signal sample autocorrelation (SNR=5 dB，L=7)

图5 基于信号采样自相关的步进宽带频谱检测图(SNR=-5 dB，L=10)Fig.5 Detected diagram of step-by-step wideband spectrum sensing based on signal sample autocorrelation (SNR=-5 dB，L=10)

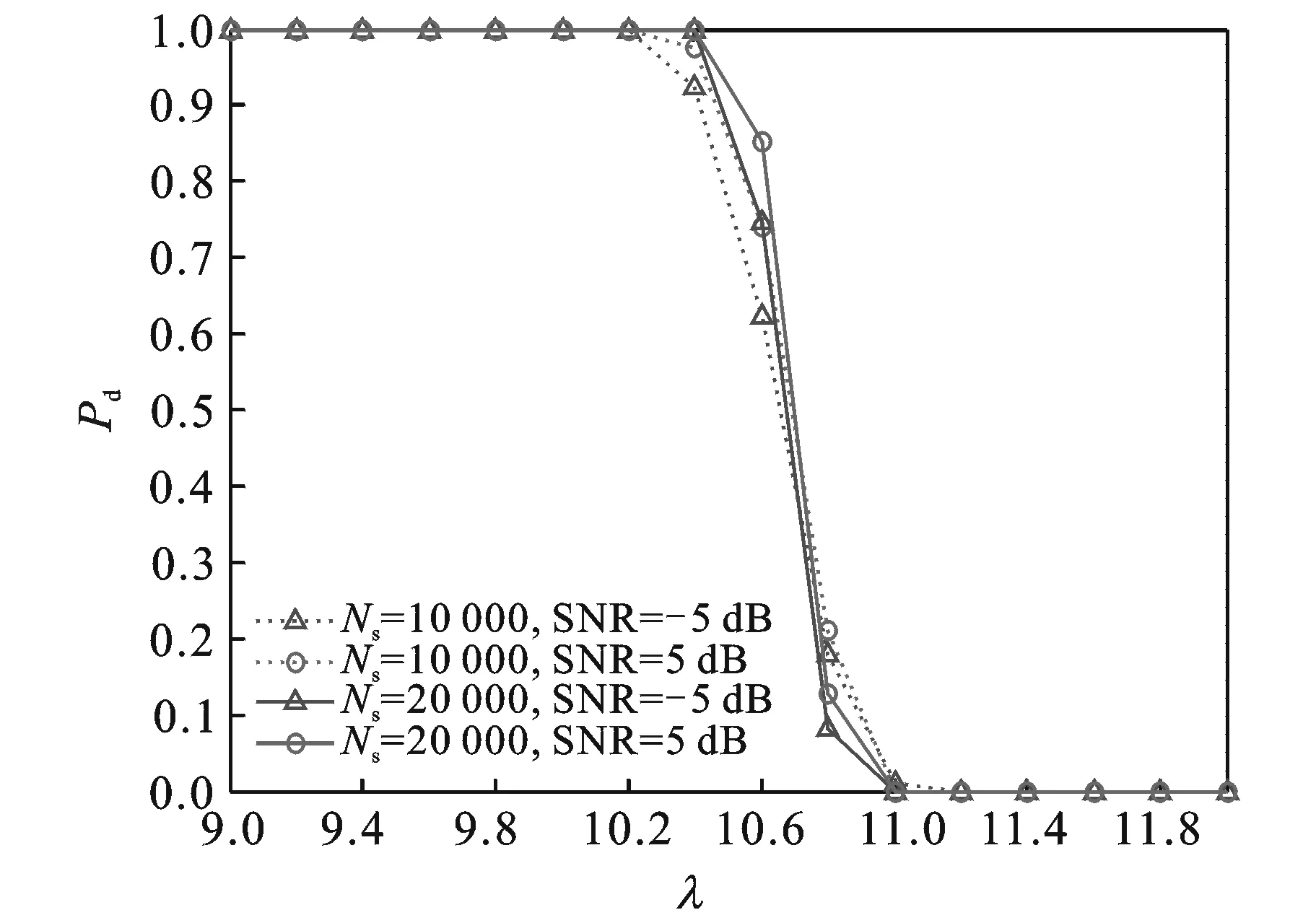
图6 不同Ns下检测门限和检测概率的关系(L=10)Fig.6 Detection probability versus decision threshold with different Ns (L=10)

同样地，Ns也会影响采样自相关检测算法的性能。图6仿真了不同信噪比下，Ns与检测性能的关系。由图6可知，随着Ns从10 000增加到20 000时，为了满足检测概率Pd≥0.95，检测门限的最大值从10.0增加到10.5。在信噪比固定不变时，Ns变化对门限值的选取有一定的影响，同样在一定程度上也决定了算法的复杂程度。实际中，在满足一定检测性能的条件下，应选择一个相对较小的Ns。本文仿真中，Ns大于40 000。

单步信号采样自相关检测算法的计算复杂度：接收信号的自相关运算的加法和乘法均为LNs，计算Tall和Tdiag需要L2次乘法，因此算法总体的乘法和加法约是LNs+L2次。以目前的软件和硬件处理能力而言，加法运算所耗费的时间可忽略不计。因而，在满足一定检测性能的要求下，尽可能选取小的L和Ns可以减少信号采样自相关检测算法的复杂度。

在频谱检测中，若检测时间过长，虽然检测性能可能提高，但是传输数据的时间就会大大缩短，不利于数据传输。因此检测时间对检测性能的影响也是需要考虑的因素之一，下面仿真检测时间与检测性能的关系。在每200 kHz的窄带信号采样自相关检测中，设置N=3 000，代替前面仿真中设置的N=2 000。

在N=3 000时，SNR分别为-5 dB和5 dB的情况下，检测门限与检测概率之间的关系如图7所示。在相同的SNR下，为了使检测概率Pd≥0.95，随着平滑因子从7增大到10，所需的检测门限值从9.0增加到11.0左右；与图1中N=2 000的仿真结果相比，为了满足同样的Pd条件，N=3 000所需的检测门限值增大。

在N=3 000且SNR分别为-5 dB和5 dB的情况下，检测门限与虚警概率之间的关系如图8所示。在同样的SNR下，为了使Pfa≤0.05，随着平滑因子从7增大到10时，所需的检测门限值从7.0增加到9.0左右，与图2中N=2 000的仿真结果相比，满足同样的Pfa的条件，N=3 000时所需的检测门限值增大。

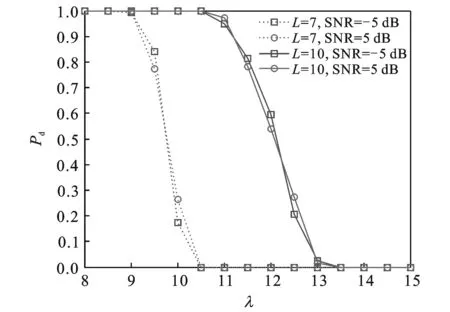
图7 不同平滑因子L下检测门限与检测概率的关系(N=3 000)Fig.7 Detection probability versus decision threshold with different L (N=3 000)

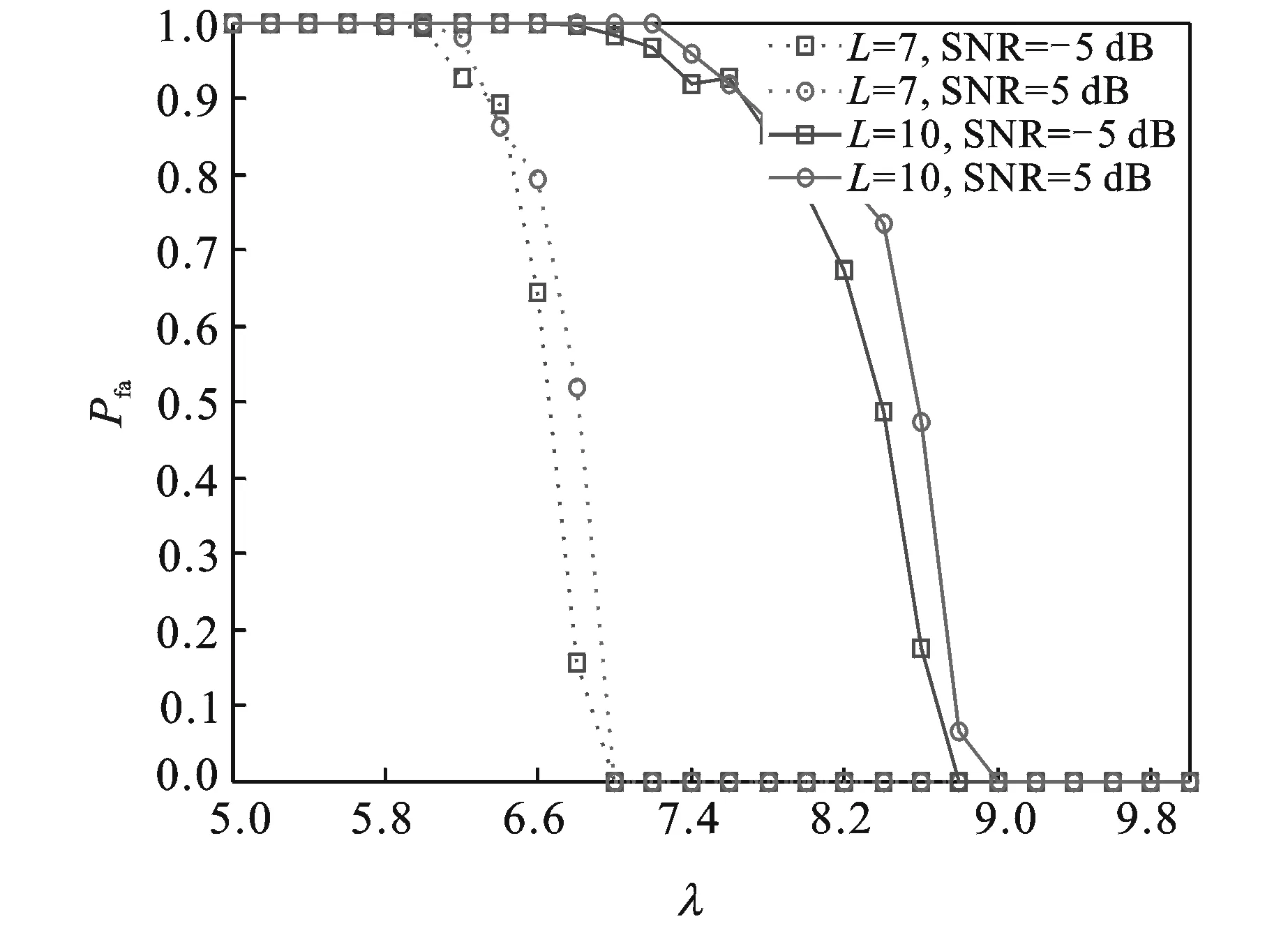
图8 不同平滑因子L下检测门限与虚警概率的关系(N=3 000)Fig.8 False-alarm probability detection versus decision threshold with different L (N=3 000)

在采用步进方法的检测中，若是采用较大的步进值(如2 MHz)进行检测，那么检测算法只能对(0, 2 MHz)，…，(18 MHz, 20 MHz)这10个窄带范围内的信号进行检测，能检测到4～8 MHz和14～18 MHz两个频段，而本文采用较小的步进值(如200 kHz)的算法能检测到5～7 MHz和15～17 MHz这两个频段。可以看出，采用较大步进值的步进检测算法的准确性将大大降低。而采用较小步进值的检测算法的准确性更高，但检测时间会变长。因此，结合较小步进值和较大步进值的宽带频谱检测算法可以获得较高的频带带宽检测的准确性，同时也缩短了GNU radio现有步进检测方法的检测时间。

4 结束语

当需要检测的带宽范围大于硬件设备的最大检测带宽时，设备不能一次性完成整个宽带频谱的检测，而采用步进宽带的能量频谱检测法可以提高在软件无线电平台的宽带频谱感知的带宽范围，但是能量检测算法易受噪声不确定性的影响。本文提出基于信号采样自相关的步进宽带频谱检测算法，不仅对噪声不确定性有很好的鲁棒性，而且能准确得出空白频谱和占用频谱的带宽位置。首先介绍了信号采样自相关检测的原理，并描述了基于信号采样自相关的步进宽带频谱检测流程，然后利用 MATLAB仿真得出其检测性能，结合仿真结果讨论影响其判决门限的相关因素。仿真实验中兼顾一定要求下的检测概率和虚警概率来选定单步的信号采样相关检测的判决门限值。仿真实验表明，选取不同的判决门限会影响检测概率和虚警概率。信噪比不变时，为达到一定的检测概率和虚警概率的要求，所需的判决门限值随着平滑因子L的增大而增大。而在平滑因子相同的情况下，改变信噪比时，所需的判决门限值也随之变化，但变化不大。由仿真实验可得，本文提出的算法能达到所要求的检测性能。此外，步进值越小，检测精度越高，但检测时间越长。当占用带宽何占用位置均未知时，合适的步进值不易选取。本文提出改变步进值的信号采样自相关的步进宽带频谱检测算法算法，结合较大步进值和较小步进值两阶段的频谱检测，可以提高频带带宽的分辨率，同时也缩短了检测时间。

参考文献:

[1] Cabric D, Mishra S M, Brodersen R W. Implementation issues in spectrum sensing for cognitive radios [C]//In Proc The Thirty-Eighth Asilomar Conference. Pacific Grove, CA, USA: IEEE， 2004:772-776.

[2] Sonnenschein A, Fishman P M. Radiometric detection of spread-spectrum signals in noise of uncertainty power[J]. IEEE Trans Aerosp Electron Syst, 1992,28(3):654-660.

[3] Tandra R, Sahai A. Fundamental limits on detection in low SNR under noise uncertainty[C]//In Proc Wireless Com. Maui, HI,USA:IEEE,2005:464-469.

[4] Cabric D, Tkachenko A, Brodersen R W. Spectrum sensing measurements of pilot, energy, and collaborative detection[C]//In Proc Military Communications Conference (MILCOM). Washington, DC,USA:IEEE,2006:1-7.

[5] Gardner W A. Exploitation of spectral redundancy in cyclostationary signals[J]. IEEE Signal Processing Magazine, 1991,8(2):14-36.

[6] Zeng Yonghong, Liang Yingchang. Eigenvalue based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications, 2009,57(6):1784-1793.

[7] Digham F F, Alouini M-S, Simon M K. On the energy detection of unknown signals over fading channels[C]//Int Conf on Commun. New York,USA:IEEE,2003:3575-3579.

[8] Zeng Yonghong, Liang Yingchang. Covariance based signal detections for cognitive radio[C]//2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks. Dublin, Ireland: IEEE, 2007:202-207.

[9] Zeng Yonghong, Liang Yingchang. Spectrum-sensing algorithms for cognitive radio based on statistical covariances[J]. IEEE Transactions on Vehicular Technology,2009,58(4):1804-1815.

[10] 李彬.基于信号采样自相关的频谱检测技术研究[D].云南:云南民族大学,2011.

Li Bin. Signal detection based on sample autocorrelation in Rayleigh fading channel[D]. Yunnan: Yunnan Minzu University, 2011.

[11] Quan Z, Cui S, SAYED A H, et al.Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J]. IEEE Trans Signal Process, 2009,57(3):1128-1140.

[12] 董淑雅,伍小芹,白勇.基于步进频域能量检测的宽带频谱感知方法研究[J].海南大学学报(自然科学版),2016,34(3):215-220.

Dong Shuya,Wu Xiaoqin,Bai Yong. Wideband spectrum sensing method based on step by step frequency domain energy detection[J]. Natural Science Journal of Hainan University, 2016,34(3):215-220.

[13] 石磊.认知无线电中空闲频谱检测技术的研究[D]. 哈尔滨:哈尔滨工业大学,2010.

Shi Lei. Research on idle spectrum detection technologies in cognitive radio[D]. Harbin: Harbin Institute of Technology, 2010.

[14] Liu Y, Zeng C, Wang H, et al. Energy detection threshold optimization for cooperative spectrum sensing[C]//Advanced Computer Control(ICACC). Shenyang, China: IEEE, 2010,4(27-29):566-570.

[15] 刘子扬,彭涛,郭海波，等.干扰系统先验信息未知的宽带能量检测[J].北京邮电大学学报, 2012,35(5):31-35.

Liu Ziyang, Peng Tao, Guo Haibo, et al. Energy detection about broadband signal without priori information of interference system[J]. Journal of Beijing University of Posts and Telecommunications, 2012,35(5):31-35.

[16] 孙哲.特征值频谱感知算法的研究及改进[D].西安:西安电子科技大学,2014.

Sun Zhe. Research and improvement on eigenvalue based spectrum sensing algorithm[D].Xi′an: Xidian University, 2014.

Step-by-StepWidebandSpectrumSensingMethodBasedonSignalSampleAutocorrelation

Chen Lu， Wu Xiaoqin， Bai Yong

(State Key Lab of Marine Resource Utilization in South China Sea, Hainan University, Haikou, 570228, China)

The bandwidth of spectrum sensing can be enlarged in software radio platform by using multi-step frequency domain energy detection. Nevertheless, the energy detection is sensitive to noise uncertainty, and signal sample autocorrelation method is robust to it. To improve the detection performance of software radio, a step-by-step wideband spectrum sensing method based on signal sample autocorrelation is proposed. Firstly, the principle of signal sample autocorrelation and a step-by-step wideband spectrum sensing procedure based on it are described. Then, the whole procedure for wideband spectrum sensing using MATLAB is simulated. The simulation results demonstrate that our proposed method can achieve the required detection performance under different signal-noise ratio (SNR). In addition, to balance the bandwidth resolution and the detection speed, we further propose to apply variable step values in two stages of wideband spectrum sending based on signal sample autocorrelation detection, which can obtain higher detection resolution of the frequency bandwidth and shorter detection time.

software radio; spectrum sensing; sample autocorrelation; signal detection; detection performance

国家自然科学基金(61561017，61261024)资助项目；海南省自然科学基金(ZDKJ2016015)资助项目。

2016-09-18；

2017-05-04

TN92