利用时差的单站无源相干定位最大似然算法

赵勇胜 宋 艳 赵拥军 赵 闯

(1. 解放军信息工程大学导航与空天目标工程学院，郑州，450001；2. 河南广播电视大学机电工程学院，郑州，450008)

利用时差的单站无源相干定位最大似然算法

赵勇胜1宋 艳2赵拥军1赵 闯1

(1. 解放军信息工程大学导航与空天目标工程学院，郑州，450001；2. 河南广播电视大学机电工程学院，郑州，450008)

针对利用单个观测站接收多个第三方辐射源信号来估计目标位置的无源相干定位问题，提出了一种基于最大似然的时差定位算法。首先根据时差测量与目标位置之间的函数关系，构建目标位置的似然函数;然后采用牛顿迭代算法求解非线性似然函数的全局极大值，从而得到目标位置估计；推导了目标位置的最小二乘解，并将其作为牛顿迭代的初始解，从而保证算法的收敛性；最后还推导了算法的理论误差和克拉美罗界，并证明两者相等。仿真结果表明，算法的定位精度优于现有算法，且在测量误差适中时，定位精度可以达到克拉美罗界。通过几何精度因子图，分析了目标位置、外辐射源数量和位置等因素对定位精度的影响。

最大似然；单站；无源定位；时差；牛顿迭代；最小二乘

引 言

无源雷达利用环境中现有的第三方辐射源来探测和定位目标。由于自身不需要辐射电磁波，因此具有成本低、隐蔽性高和不占用频谱资源等优点，并且由于收发分置的工作模式和较低的工作频段，无源雷达还具有探测隐形目标的能力[1]。基于此，无源雷达可以与传统主动雷达形成优势互补，从而建立起可靠、高效的探测预警网络。

无源雷达工作的基本原理是通过接收第三方辐射源的直达波信号和经过目标反射后的回波信号，并比较两路信号的到达时间差(Time difference of arrival, TDOA)，从而确定目标的位置[2]。相比于传统的多站被动定位系统[3]，单站定位系统具有机动性高、不存在多站同步问题等优势[4]。随着环境中可用辐射源数量的日益增多[5-9]，单部接收机往往可以同时接收到多个辐射源的信号，而辐射源数量的增加意味着定位精度的提高[10]。因此，研究基于单站多外辐射源的无源定位方法具有重要意义。然而，要通过对目标的一次时差测量来确定目标的位置并不容易,原因在于时差测量关于目标的位置是高度非线性的，难以得到目标位置的解析解。对于非线性定位问题，传统的泰勒迭代方法可以较小的计算量得到接近克拉美罗界(Cramer Rao lower bound, CRLB)精度的解[11]。但泰勒迭代方法需要给定较为准确的初始解，否则难以收敛至全局最优解。文献[12]针对利用单站多外辐射源的时差定位模型，提出了一种基于正则化约束总体最小二乘(Regularized constrained total least square, RCTLS)的时差定位算法。在测量误差较小时，算法的定位精度可以达到CRLB，但该算法在理论上是一种有偏估计算法，在TDOA测量误差较大时，定位误差会迅速偏离CRLB。

最大似然估计(Maximum likelihood estimator, MLE)理论上是最优估计算法[13]。本文针对单站多外辐射源条件下的时差定位问题，提出了一种基于最大似然的目标位置估计算法。针对建立的似然函数关于目标位置非线性的问题，利用牛顿迭代方法得到似然函数全局极大值对应的目标位置估计。牛顿迭代算法具有良好的收敛性，但考虑到其本质上仍是一种局部最优算法，推导了目标位置的最小二乘解，并将其作为牛顿迭代的初始解，从而保证了算法能够收敛至全局最优解。

1 定位场景

本文考虑的无源雷达定位模型如图1所示,场景中存在N个第三方辐射源，1个目标和1个观测站。观测站上布设了两副天线，分别用于接收直达波信号和目标回波信号[14]。

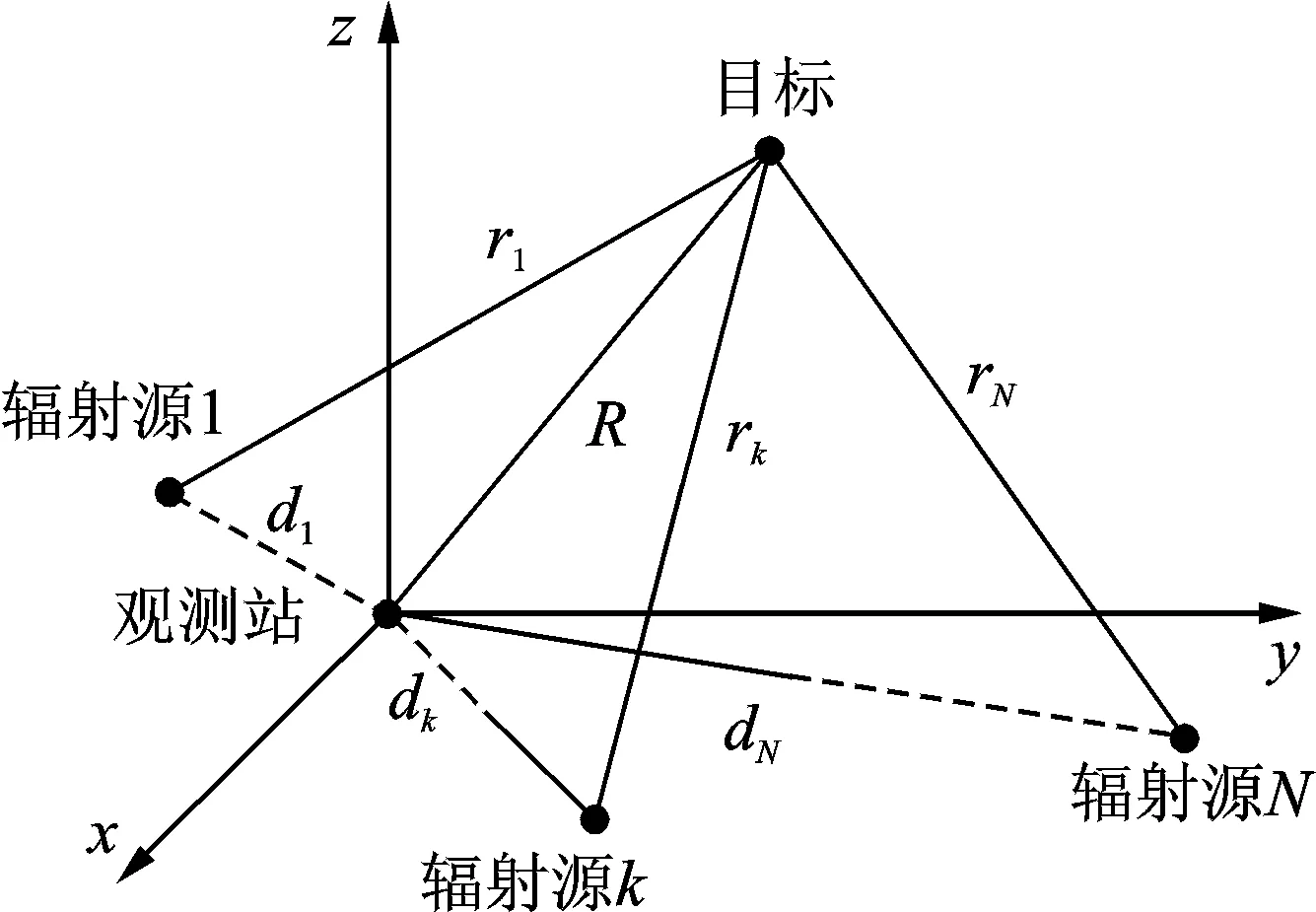
图1 单站多外辐射源定位模型 Fig．1 Single-observer multi-illuminators localization

假设将观测站作为原点，第k个辐射源位于Xk=(xk,yk,zk)T(k=1,2,…,N)，目标位于X=(x,y,z)T。由于待估计的目标位置参数共有3个，因此本文单站多外辐射源定位系统至少需要3个辐射源，以构造3个时差方程，从而实现对目标位置的估计。

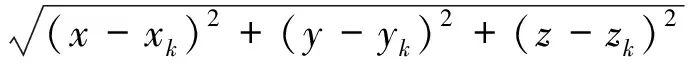
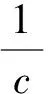
(1)

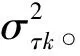
联合场景中的全部N个辐射源，得到矩阵形式的观测方程为

(2)

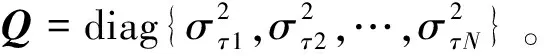
2 定位算法

2.1 最大似然估计

(3)

需要强调的是，实际应用中协方差矩阵Q可能并非对角矩阵，但对于算法的成立不会造成影响。

对式(3)取对数，并去掉与目标位置参数X无关的常数项，从而得到X的对数似然函数为

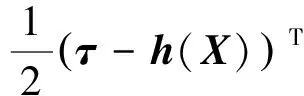
(4)

那么X的最大似然估计为

(5)

显然，L(X)全局极大值所在的位置即为X的最大似然估计。

2.2 牛顿迭代

式(4)中的似然函数L(X)关于X是非线性的，因此难以通过解析解的方式得到其全局极大值，本文采用牛顿迭代算法来得到似然函数的全局极大值。

首先，根据L(X)，构造牛顿迭代的目标函数为F(X)=0.5[τ-h(X)]TQ-1[τ-h(X)]。假设目标位置的初始解为X0，将F(X)在X0处展开，并忽略三阶及以上的误差项，得

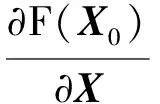
(6)

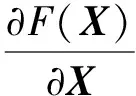
(7)

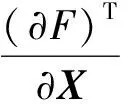
(8)

(9)

假设bij为B中的第i行第j列元素，Xi为X的第i个变量，则

(10)

从式(7)可得

X=X0-B-1A

(11)

牛顿迭代算法具有二阶收敛性，但从式(11)可以看出，其迭代过程需要给定初始解。为此，本文推导目标位置的最小二乘解，并将其作为迭代的初始解。

2.3 最小二乘定位

首先，假设不存在测量误差，那么将式(1)移项整理，可得

R+rk=cτk+dk

(12)

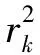
(13)

将式(12)代入式(13)，整理可得

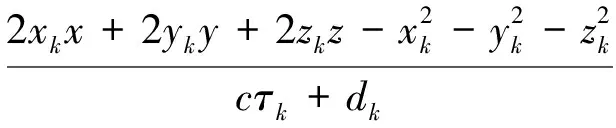
(14)

将式(12，14)相加，可得

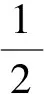
(15)

经过上述转化，式(1)中非线性的时差方程被转化为了式(15)中的线性形式,表示成矩阵形式为

HX=b

(16)

式中

(17)

(18)

显然，式(16)的最小二乘解为

(19)

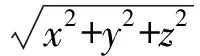
由于忽略了测量误差的影响，式(19)得到的最小二乘解并不是全局最优解，但将其作为初始解，经过牛顿迭代后，可收敛至全局最优解。

3 性能分析

3.1 克拉美罗界

CRLB是无偏估计算法估计精度的理论极限，将其作为参考，可以评估算法的估计性能。根据CRLB的定义，对式(3)中PDF取对数，并关于X求导，可得

(20)

式中:Xi表示向量X中的第i个变量。设J(X)为系统的Fisher信息矩阵(Fisher information matrix, FIM)。根据定义，J(X)可表示为

(21)

将式(20)代入式(21)，得到J(X)矩阵中的各元素为

CRLB为FIM矩阵的逆。于是对式(21)取逆矩阵，得

CRLB (X) =J-1(X)=[G(X)TQ-1G(X)]-1

(22)

则算法定位的均方误差MSE应当满足

(23)

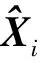
3.2 理论误差

假设算法的定位误差为ΔX，那么

(24)

算法得到最大似然解的必要条件为一阶偏导为0,将式(24)代入式(8)，并在真实值X处进行一阶泰勒展开，即

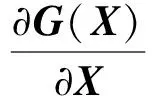
(25)

忽略式(25)中的二阶误差项，可得

[G(X)]TQ-1[v-G(X)ΔX]=0

(26)

从式(26)中可得

ΔX=[G(X)TQ-1G(X)]-1G(X)TQ-1v

(27)

由式(27)可得算法估计误差的协方差矩阵为

cov(ΔX)=[G(X)TQ-1G(X)]-1

(28)

比较式(28)中算法的理论误差与式(22)中CRLB。显然，算法的理论误差可以达到CRLB。

4 仿真实验

通过设置仿真定位实验，来检测算法的定位性能。实验场景设置如下：假设空间中有8个第三方辐

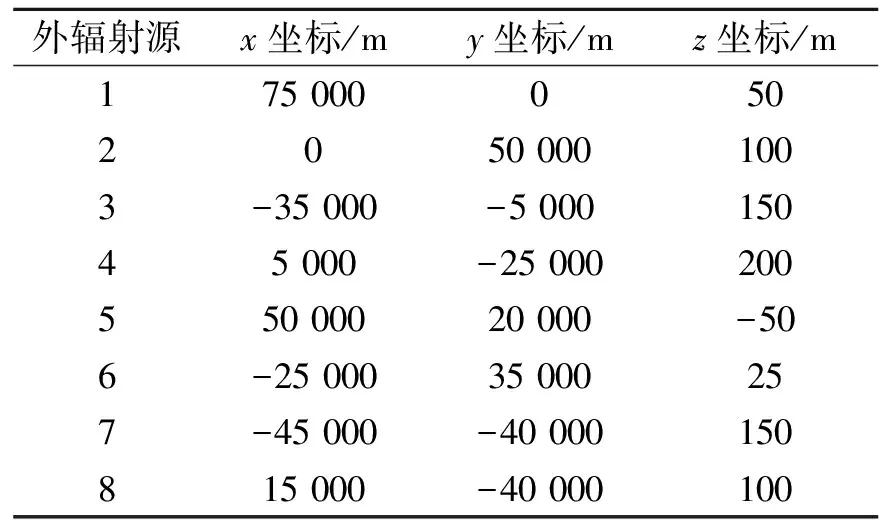
表1 外辐射源位置

射源，位置如表1所示。目标位于[10 000,10 000,10 000]Tm。根据文献[15]，将时差的测量误差统一设置为1～1 000 ns。通过统计算法的均方根误差和偏差，来评估算法的性能。

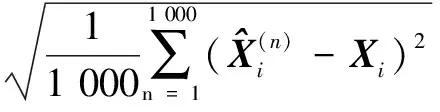
(29)

(30)

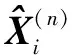
4.1 不同的时差测量误差条件下算法的定位误差(仿真1)

在不同时差测量误差的条件下，利用本文算法进行仿真定位实验，统计算法的RMSE和Bias，并将本文算法的定位结果与文献[12]中的算法及CRLB对比。外辐射源选取表1中的第1～4个外辐射源。图2和图3分别给出了时差测量误差为1～1 000 ns时，算法定位的均方根误差和偏差。

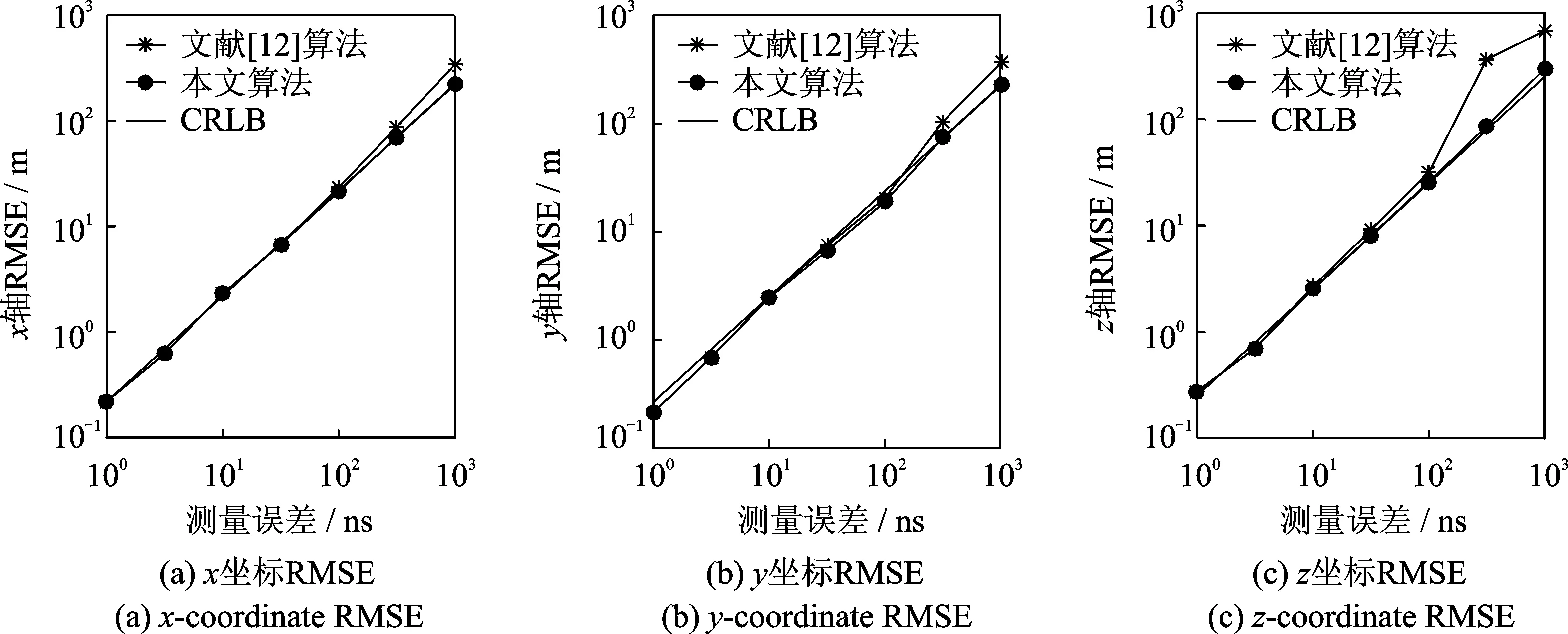
图2 不同时差测量误差条件下算法的均方根误差Fig．2 RMSE of the proposed algorithm for different TDOA measurement errors

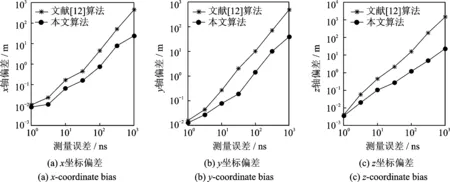
图3 不同时差测量误差条件下的算法偏差Fig．3 Bias of the proposed algorithm for different TDOA measurement errors

由图2可以看出，本文算法的定位RMSE逼近CRLB。与文献[12]算法相比，文献[12]算法在时差测量误差小于30 ns时可以逼近CRLB，而当时差测量误差大于30 ns时，算法的估计误差开始迅速偏离CRLB，而在此测量误差条件下，本文算法仍能给出达到CRLB精度的位置估计。由图3可以看出，由于文献[12]算法是一种有偏估计算法，因此其偏差始终高于本文算法，并且随着时差测量误差的增加，文献[12]算法的偏差增大的速度也快于本文算法。

4.2 系统几何精度因子图分析(仿真2)

通过计算系统几何精度因子(Geometric dilution of precision, GDOP)来分析目标处于不同位置时算法的定位性能。GDOP的定义为

(31)

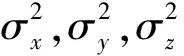
PX=E(ΔXΔXT)= [G(X)TQ-1G(X)]-1

(32)

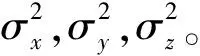
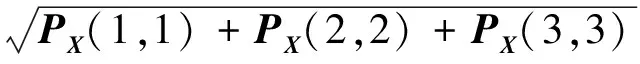
(33)

图4给出了目标高度分别为2 000 m和20 000 m及外辐射源数量分别为4个和8个时，系统的GDOP图，其中黑色三角形为外辐射源所在位置。比较图4(a)和图4(b)，可以分析出在4个外辐射源条件下，不同的目标高度对GDOP的影响：在x,y坐标相同时，目标高度越高，定位误差越小;目标位于外辐射源和观测站所在的中央区域上方时，定位误差最小，随着目标远离该中心区域，定位误差增大。而从图4(b)和4(c)的对比可以看出，在目标位置相同时，外辐射源数量越多，定位精度越高。

图4 在不同的目标高度和不同的外辐射源数量条件下系统的GDOP图(时差测量误差10 ns)Fig．4 GDOP figures for different target heights and different illuminator numbers (TDOA measurement error with 10 ns)

5 结束语

本文研究了如何利用单个观测站接收多个外辐射源的信号，从而实现对目标定位的问题。以外辐射源直达信号和目标回波信号到达观测站的时差作为观测量，得到了目标位置的最大似然估计。根据时差与目标位置之间的函数关系推导了目标位置的似然函数；利用牛顿迭代方法求解非线性似然函数，得到目标位置的最大似然估计；将时差方程伪线性化处理，推导了目标位置的最小二乘解，并将其作为牛顿迭代的初值；推导了算法的理论误差和CRLB，并从理论上证明了本文算法的理论误差可以达到CRLB。通过仿真实验表明，本文算法的定位误差低于文献[12]算法，在时差测量误差较大时仍能达到CRLB。

[1] He Qian, Rick S B. The significant gains from optimally processed multiple signals of opportunity and multiple receive stations in passive radar[J]. IEEE Signal Processing Letters, 2014, 21(2): 180-184.

[2] Subedi S, Zhang Y D, Amin M G, et al. Motion parameter estimation of multiple ground moving targets in multi-static passive radar systems[J]. Eurasip Journal on Advances in Signal Processing, 2014, 1(157): 1-14.

[3] Lin L, So H C, Chan F K W, et al. A new constrained weighted least squares algorithm for TDOA-based localization[J]. Signal Processing, 2013， 93(11): 2872-2878.

[4] 黄耀光, 高博, 李建新, 等. 基于平方根UKF双向滤波的单站无源定位算法[J]. 数据采集与处理, 2013, 28(2): 207-212.

Huang Yaoguang, Gao Bo, Li Jianxin, et al. Single-observer passive location algorithm based on square-root UKF with forward-backward filtering[J]. Journal of Data Acquisition and Processing, 2013, 28(2): 207-212.

[5] Wang H, Wang J, Zhong L. Mismatched filter for analogue TV-based passive bistatic radar[J]. IET Radar, Sonar and Navigation, 2011, 5(5): 573-581.

[6] Zhu Jiabing, Tao Liang, Hong Yi. Study on moving target detection to passive radar based on FM broadcast transmitter[J]. Journal of Systems Engineering and Electronics, 2007, 18(3): 462-468.

[7] Michael E, Alexander S, Fabienne M. Design and performance evaluation of a mature FM/DAB/DVB-T multi-illuminator passive radar system[J]. IET Radar, Sonar and Navigation, 2014, 8(2): 114-122.

[8] Sun H, Tan DKP, Lu Y, et al. Applications of passive surveillance radar system using cell phone base station illuminators[J]. IEEE Aerospace and Electronic Systems Magazine, 2010, 25(3): 10-18.

[9] Colone F, Falcone P, Bongioanni C, et al. WiFi-based passive bistatic radar: Data processing schemes and experimental results[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1061-1079.

[10] 李晶, 李冬海, 赵拥军. 利用角度和时差的单站外辐射源定位方法[J]. 武汉大学学报(信息科学版), 2015, 40(2): 227-232.

Li Jing, Li Donghai, Zhao Yongjun. Single-observer passive coherent location estimation based on DOA and TDOA[J]. Geomatics and Information Science of Wuhan University, 2015, 40(2): 227-232.

[11] Foy W H. Position-location solutions by Taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(2): 187-194.

[12] Li Wanchun, Wei Ping, Xiao Xianci. A robust TDOA-based location method and its performance analysis[J]. Science in China Series F: Information Sciences, 2009, 52(5): 876-882.

[13] Wang Gang, Chen Hongyang. An importance sampling method for TDOA-based source localization[J]. IEEE Transactions on Wireless Communications, 2011, 10(5): 1560-1568.

[14] He You, Zhang Caisheng, Tang Xiaoming, et al. Coherent integration loss due to pulses loss and phase modulation in passive bistatic radar[J]. Digital Signal Processing, 2013, 23(4): 1265-1276.

[15] Li Jing, Zhao Yongjun, Li Donghai. Passive multipath time delay estimation using MCMC methods[J]. Circuits System Signal Process, 2015, 34(12): 3897-3913.

MaximumLikelihoodAlgorithmforSingle-ObserverPassiveCoherentLocationUsingTDOAMeasurements

Zhao Yongsheng1, Song Yan2, Zhao Yongjun1, Zhao Chuang1

(1. School of Navigation and Aerospace Engineering, PLA Information Engineering University, Zhengzhou, 450001, China;2. School of Mechanical and Electrical Engineering, Henan Radio and Television University, Zhengzhou, 450008, China)

To solve the single-observer passive location estimation using multiple illuminators of opportunity, a time difference of arrival(TDOA) location algorithm based on maximum likelihood is proposed. Firstly, according to the functional relationship between the TDOA measurements and the target location, the likelihood function of the target location is constructed. Then Newton′s method is applied to obtain the global maximum of the nonlinear likelihood function and determine the target position. The least squares solution of the target location is derived and used as the initial guess of the Newton′s method. Finally, the theoretical error and the Cramer Rao Lower Bound (CRLB) are also derived and proved to be equal. Simulation results demonstrate that the proposed algorithm outperforms existing algorithms and achieves the CRLB at moderate noise level. Moreover, from the geometric dilution of precision figure, the influence of target position, illuminator number and position on the localization accuracy is analyzed.

maximum likelihood (ML);single-observer; passive location; time difference of arrival (TDOA); Newton′s method; least squares (LS)

国家自然科学基金(61401469)资助项目；国家高技术研究发展计划(2012AA7031015)资助项目。

2015-10-29；

2016-05-03

TN971

A

赵勇胜(1990-)，男，硕士研究生，研究方向: 无源定位,E-mail:alwayswinzys@163.com。

赵闯(1978-)，男，博士研究生，讲师，研究方向：雷达信号处理,E-mail:rushzhaotg@163.com。

宋艳(1985-)，女，硕士，助教，研究方向：电子设计自动化,E-mail:songxiaoyuner@163.com。

赵拥军(1964-)，男，教授，博士生导师，研究方向：雷达信号处理、阵列信号处理,E-mail:zhaoyongjuntg@126.com。