基于灰度直方图的MR脑组织的提取方法

，，，,2

(1.中国计量大学 信息工程学院，杭州 310018; 2. 北卡罗来纳大学教堂山分校 医学院，美国)

基于灰度直方图的MR脑组织的提取方法

朱冠菲1，徐永秋1，米红妹1，朱建明1,2

(1.中国计量大学信息工程学院，杭州310018; 2.北卡罗来纳大学教堂山分校医学院，美国)

根据脑磁共振图像(magnetic resonance imaging，MRI)的灰度直方图中不同峰值对应不同的脑组织灰度分布的特点，提出了一种基于灰度直方图提取MR图像中脑组织的方法；首先，为了克服传统方法主观选择门限阈值等方面的不足，利用多项式曲线拟合灰度直方图获取区域生长门限阈值确定最优种子点，并结合形态学重构方法进行颅骨分离，对脑MR图像进行了预处理；然后，结合K均值聚类算法通过对灰度直方图多峰值的选取确定初始聚类中心，将颅骨剥离后的脑组织图像高效、精确地细化分割出脑脊液、灰质、白质；文中分别使用了模拟脑MRI数据以及真实脑部MRI数据进行测试，对分类结果进行定性、定量的分析，并与模糊C均值算法进行比较；结果表明，该方法提高了提取脑组织的工作效率和准确度。

灰度直方图；曲线拟合；区域生长；K均值；脑组织提取

0 引言

核磁共振图像(magnetic resonance imaging，MRI)脑组织提取在神经图像分析中是配准、脑组织分类等的预处理步骤，起着重要作用[1]。在实际应用中，受图像噪声、灰度不均匀性等影响，给脑MR图像的精准分割造成困难和挑战[2-3]。

目前，脑组织分类和提取有大体可以分为三类：基于活动轮廓模型，基于形态学和基于图像灰度。基于活动轮廓的有：Sudipta R[4]等使用水平集产生递阶结构进行脑组织的三类分割和提取。基于形态学的有：陈筱[7]等和王大溪[8[9]等开发了非局部均值扩散(nonlocal means diffusion,NLD)算法, 进行组织灰度相似性统计，田换[10]等提出图割和K均值相结合的算法对脑MRI图灰度不均匀性进行了处理并细化达到分割脑白质和脑灰质的目的。其中基于灰度分割的主流方法是上述的聚类方法。传统的模糊C均值(Fuzzy C Means, FCM)算法对参数初始值十分敏感，随机产生初始聚类中心，用户选定的种子点主观性强，导致脑MR图像分割结果不稳定。为了克服FCM对参数初始值敏感的问题，本文提出了一种基于灰度直方图的提取磁共振图像脑组织的方法。首先，对磁共振脑图进行交互式操作，利用多项式曲线拟合灰度直方图得到选取区域生长全局阈值以确定最优种子点进行颅骨剥离，并记录各峰谷值，再通过对灰度直方图多峰值的选取确定初始聚类中心，最后采用K均值聚类方法达到分割脑白质、脑灰质和脑脊液的目的。实验表明，该算法能有效准确的从脑MRI图中分割出脑白质、脑灰质和脑脊液。

1 基于灰度直方图的图像预处理

直方图在医学处理中有广泛的应用，MR脑图中多个峰值对应不同的脑组织灰度分布[11]。图像的灰度直方图作为对图像各灰度值进行统计所得到的关于灰度值的函数，反映了图像中每种灰度值出现的频数。最简单直接的阈值分割是根据灰度直方图不同峰值进行初步预选，主观性强。脑组织主要包括脑白质、脑灰质以及脑脊液，3种组织在图中的灰度差异比较明显。一幅典型无噪声T1加权脑MRI图(见图1)的灰度直方图如图2所示。可见除去背景为零的峰，有3种峰值灰度差异较大，其相对应脑白质、脑灰质以及脑脊液3种脑组织。

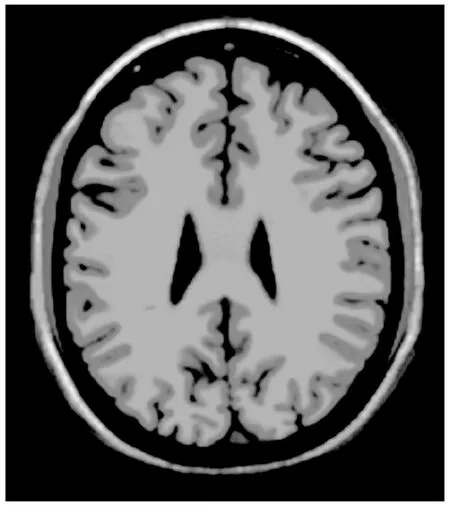
图1 无噪声T1加权模拟脑MRI图

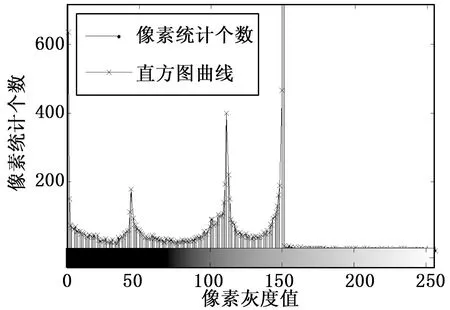
图2 图1脑MRI图对应的灰度直方图

1.1 颅骨分离

由于一幅脑MRI图像除了要分割的组织成分外，还包含颅骨和头皮等成分，这些非脑组织的成分会直接影响脑组织的分割效果，所以需要进行颅骨剥离。采用区域生长法可分割出颅骨外皮脂和颅内脑组织，该算法判定准则中需要考虑的像素与初始种子点的像素灰度值差的绝对值小于某个门限值，即全局阈值。所以全局阈值的选取非常重要。本文在得到最佳全局阈值后，结合区域生长函数及形态学处理，将颅骨去除后的脑组织图像作为先验信息，为后续提取分类脑组织做准备。

1.1.1 最佳全局阈值获取

灰度直方图存在多个峰谷，主观选取单一阈值难以达到分割的最好效果，熊平[12]等提出了一种根据CT图像的灰度直方图进行曲线拟合得到局部极小值对应的最大阈值对CT图像分割。据此，本文提出多项式曲线拟合获取局部极大值作为最佳全局阈值。最小二乘法多项式曲线拟合，是根据给定的m个像素点,并不要求这条曲线精确地经过这些点。通过给定数据点pi(xi,yi)，其中xi为像素灰度，yi为像素统计个数，i为下标，i=1,2,...,m，m为像素点个数，pi(xi,yi)即为灰度直方图上横轴灰度与纵轴统计个数所对应的点，求近似曲线y=f(x)。设拟合多项式为：

y=a0+a1x+...+akxk

(1)

式中，ai是系数，k为幂次。按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法，得到多项式系数ai，同时我们就得到了拟合曲线。

拟合函数f(x)为一连续函数且可导。令f(x)′=0一阶导便可求得像素灰度分布的局部极值。再根据二阶导f(x)′原理及其凹凸性，判断局部极大值。由系数矩阵ai求得f(x)′=0时对应的灰度x值，作为区域生长函数的最佳全局阈值。

1.1.2 基于区域生长和形态学的颅骨剥离

为了得到颅骨剥离得到脑组织的先验信息，提出结合区域生长和形态学方法对整幅脑MRI图像进行颅骨剥离。

区域生长是根据预先定义的生长准则来把像素或子区域集合成较大区域的处理方法。我们先将获取的最佳全局阈值结合区域生长方法应用到脑MRI图上。图像区域内像素的相似性度量以像素灰度为准，以|Zi-S|≤T为生长准则[13]，进行不同成分之间的区域分割。Zi是被处理脑MR图的像素灰度值，参数S这里定义为颅骨外某皮脂像素的像素值，T为1.1.1章节得到的全局阈值，此原则用来测试图像中的像素是否与皮脂像素灰度(种子点)足够相似。由于骨质中无氢原子，颅骨外的皮脂等对病理研究没有意义，所以在本文算法中，颅骨与脑组织之间最大类别差值即为图像中有着该像素值的点的种子。生长分割完毕，转化为二值图像，再利用形态学重构进行脑组织提取。

数学形态学中，二值图像F=f(x,y)与结构元素B都是定义在二维笛卡尔网格上的集合。形态学算子有腐蚀、膨胀、开运算和闭运算4种[14]。利用各算子的形态学处理和阈值分割，找到脑部MRI图像除背景之外的最大的连通区域，结合区域生长方法，进行组织分割及形态学重构。重构操作需要一个标记(marker)图像h、一个掩模(mask)图像g和一个结构元素B，其中标记图像h必须是掩模图像g的子集。使用8邻域连通分量，得到模板二值图像图像J，对原图像f(x,y)进行点乘运算，便可得到颅骨分离后的脑组织图像temp。

1.2 多峰值选取

K均值的算法将图像中的像素分割成k个簇，根据某种距离原则，再分配到相似的有限元中。K均值的k个聚类单元影响整个算法的计算结果，所以找到合适的k个初始聚类中心十分重要。3种不同的脑组织的“波峰”不同，选取灰度直方图的“波峰”作为K均值的初始聚类中心方法[15]，据此，我们提出使用双边滤波及高斯分布方法[16]判断并找出图像灰度直方图的峰值与谷值。采用相似性滤波核函数Sa[16]：

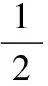
(2)

其中，p为随机给定的某像素点位置，q点为核函数对应的像素点位置，Ip为q点对应的像素值大小，Np为高斯分布中最近的峰值，σp为峰值和谷值之间的一半距离(高斯分布95%的置信区间)。循环比较各像素点灰度值与峰值对应灰度值大小，控制高斯分布参数中心和标准偏差，实现找到图像局部极值目的。除去背景的峰值，所得到的3个峰值对应3种MR脑组织。因此，我们将得到的3种峰值作为K均值的3个初始聚类值进行聚类计算。

2 基于K均值聚类算法的脑组织分类提取

K均值聚类算法由J.B.MacQueen于1967年提出的一种基于划分的经典聚类算法，算法简单高效、收敛速度快[17]。该方法可以应用在不同的领域，通常用于数据挖掘，包括图像处理，它可以用来作为基于聚类的图像分割方法。

各部分峰值为K均值算法的输入值。将1.2章节得到的局部最大峰值设定为“波峰”，作为K均值算法的初始聚类中心，并将经过颅骨分离的预处理后的脑组织图temp作为输入对象，进行脑组织的分类和提取。基于K均值聚类算法的脑组织分类提取的基本步骤描述如下：

第1步：自动获取阈值进行颅骨剥离的脑组织图temp，并得到各“波峰”对应的灰度值R(k)；

第2步：将峰值从小到大排列，作为k个数据对象依次对应的初始聚类中心；

第3步：分别计算各个数据对象即二维脑MRI灰度图到各个聚类中心的曼哈顿距离(Manhattan Distance)，根据最近邻原则min赋值逐个划分到最近的聚类中心所代表的簇中，计算误差平方和准则函数E值，即均方差总和；曼哈顿距离又称绝对距离，数学定义为：

(3)

式中，d(xi,yj)表示数据对象xi,yj之间的距离，p表示数据空间中相应的一个数据点，每个数据对象有p个属性，k=1,2,…,p。

误差平方和准则函数E定义为：

(4)

其中：E表示数据集中所有数据对象的均方差总和，mi为聚类子集xi的聚类中心点。

第4步：分别计算各个簇中所有数据对象的平均值作为新中心，重新分配数据对象，并重复2、3步骤，直到计算得到的E值和前一次得到的E值小于等于预先设定的阈值，则收敛。

第5步：输出满足终止条件的结果，即脑灰质、脑白质以及脑脊液的图。

3 实验结果与分析

本文分别使用模拟数据以及真实脑部MRI数据进行测试，软件实验平台采用Matlab2013b，算法测试硬件配置为酷睿i3处理器，2G内存。

3.1 模拟数据实验

本实验对来自BRAINWEB[18]数据库的仿真T1加权模拟脑图进行分割和组织提取。体素大小为181×217×181，无噪声和偏移场作用，层厚1 mm。选取其中一片作为示例(即原模拟脑图图1)进行灰度直方图的多项式曲线拟合并进行颅骨分割以提取脑组织，其灰度直方图多项式拟合曲线、峰值分布如图3和图4。

图3 模拟脑MRI(图1)多项式拟合曲线图

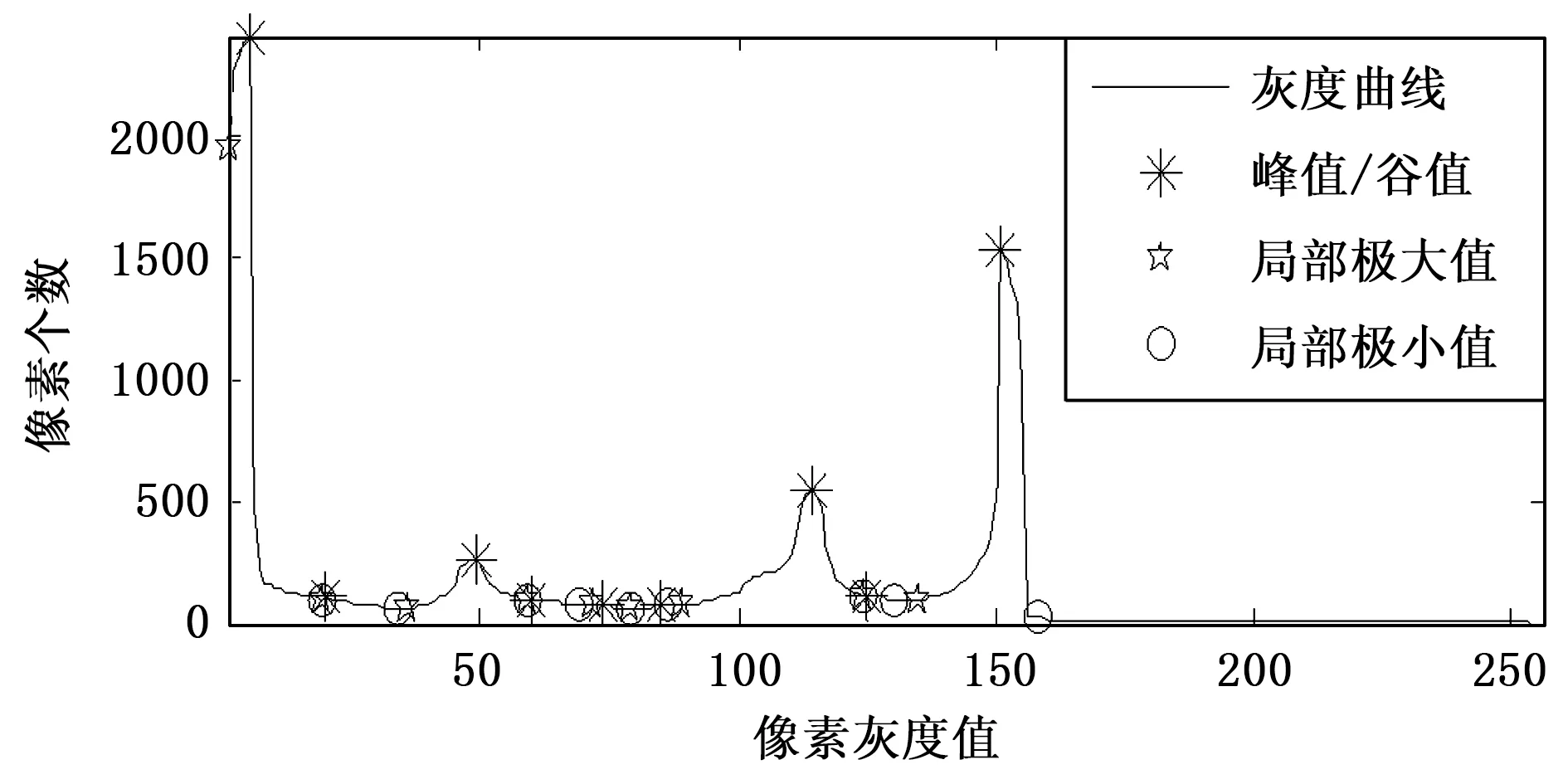
图4 模拟脑MRI图(图1)峰值分布

多项式拟合全局阈值结果以及各峰值见表1：

表1 模拟脑MRI图(图1)的灰度值参数

全局阈值代入生长函数后并进行形态学重构(详见1.1.2章节)得到剥离颅骨的脑组织图像temp，如图5(a)。将各峰值作为输入数据，灰度直方图拟合曲线得到的系列极值进行顺序排列并作为k个输入初始聚类中心，得到3种脑组织如图5(b)(c)(d)。

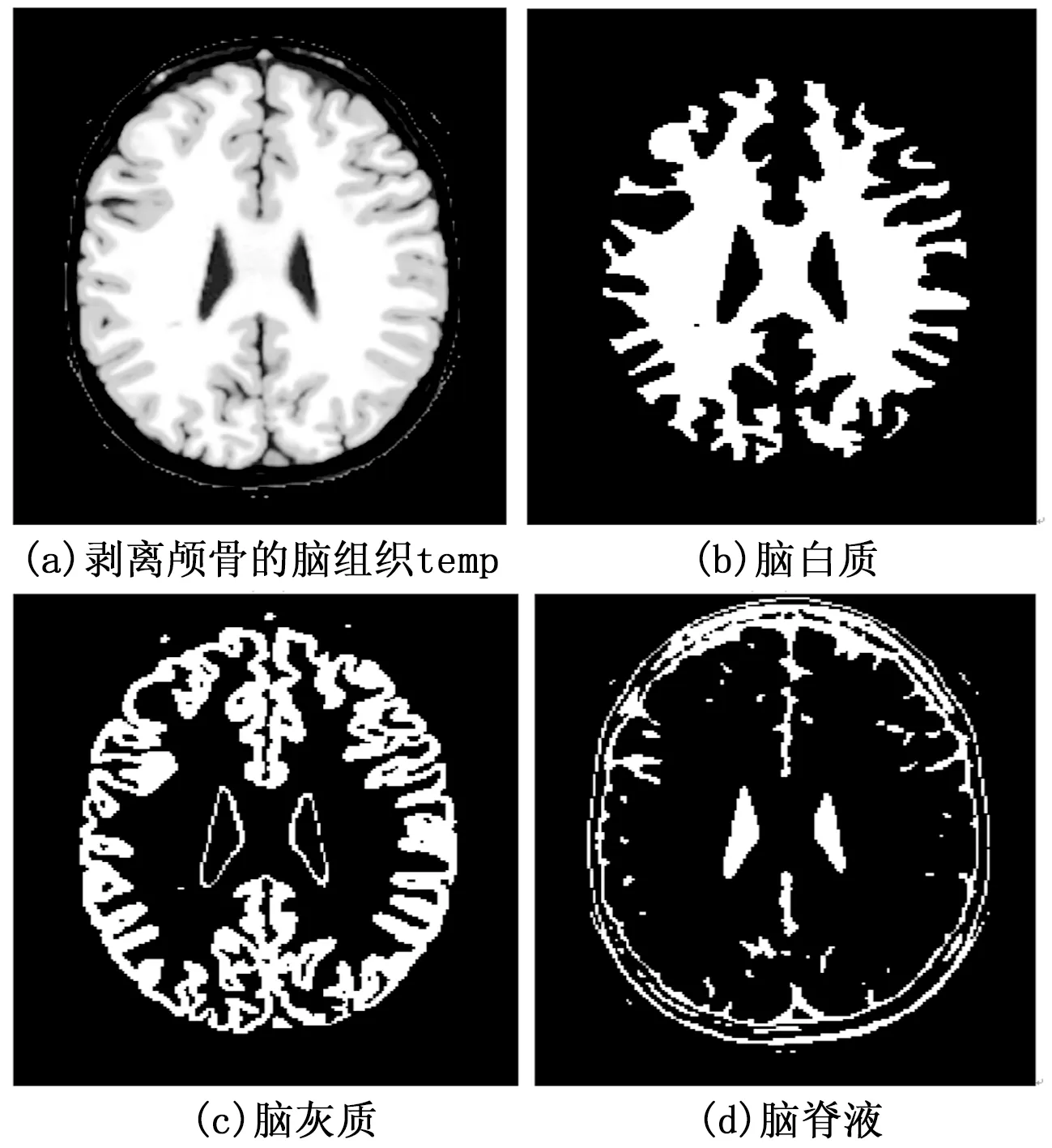
图5 MRI脑原图(图1)颅骨剥离后的脑组织部分

3.2 真实数据实验

测试真实脑MRI图像数据为医院收集的15组病人脑部磁共振T1加权图，扫描序列为快速自旋回波，1.5T的通用GE系统采集，空间分辨率为512×512。

真实脑MRI图一定存在噪声。强场越高，噪声越少。磁共振图像大多符合瑞利分布的加性噪声[19]。所以，首先对这一些列测试数据进行平滑预处理，本文采用常用的中值滤波，3×3模板进行预处理。图6展示了其中一组序列中某一病人经室间孔的横断层面，对去噪前后进行了定性对比。

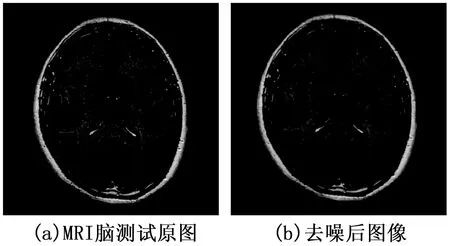
图6 某一病人经室间孔的横断层面

本文同时对去噪预处理的效果进行了定量评价。均方误差(Mean Squared Error, MSE)是衡量“平均误差”的一种较方便的方法，可以评价图像数据的变化程度。峰值信噪比(Peak Signal to Noise Ratio, PSNR) 是最普遍，最广泛使用的评鉴画质的客观量测法。均方误差越小，归一化均方误差(Normalized Mean Square Error，NMSE)[20]越小，峰值信噪比越大，说明图像质量越好，实验数据具有更好的精度。从15组病人选取出共30张经室间孔的横断层面的脑MR图进行中值滤波操作，得到的实验数据去噪后具体评价指数见表2。

表2 去噪后评价指数

由表2可知，去噪后MRI脑图的均方误差约4.2，归一化均方误差极小，而峰值信噪比达到71，由均方误差越小，峰值信噪比越大，说明图像质量越好可知，中值滤波去噪效果良好。

去噪后得到的灰度直方图、多项式拟合曲线图如图7所示，各峰值分布图如图8所示。

图7 真实脑MR图(图6(a))灰度直方图及拟合曲线 图8 真实脑MR图(图6(a))峰值分布

图6(a)真实脑MR数据的全局阈值及各峰值见表3。

表3 真实脑MR图(图6(a))灰度值参数

同模拟实验步骤，将全局阈值作为输入数据，得到二值模板J和颅骨剥离后脑组织分别如图9(a)、(b)。

本文采用商业软件SPM分割的图作为金标准(专家医生手动分割的结果 )并增加了结合传统的FCM经典算法作为对比，3种方法对图6(a)提取并分类脑组织的结果分别如图10～12。

在进行颅骨剥离等预处理操作后，将图9中提取的脑组织图(b)作为输入数据，得到的各峰值作为k个输入初始聚类中心，结合K均值算法进行脑组织的分类提取。

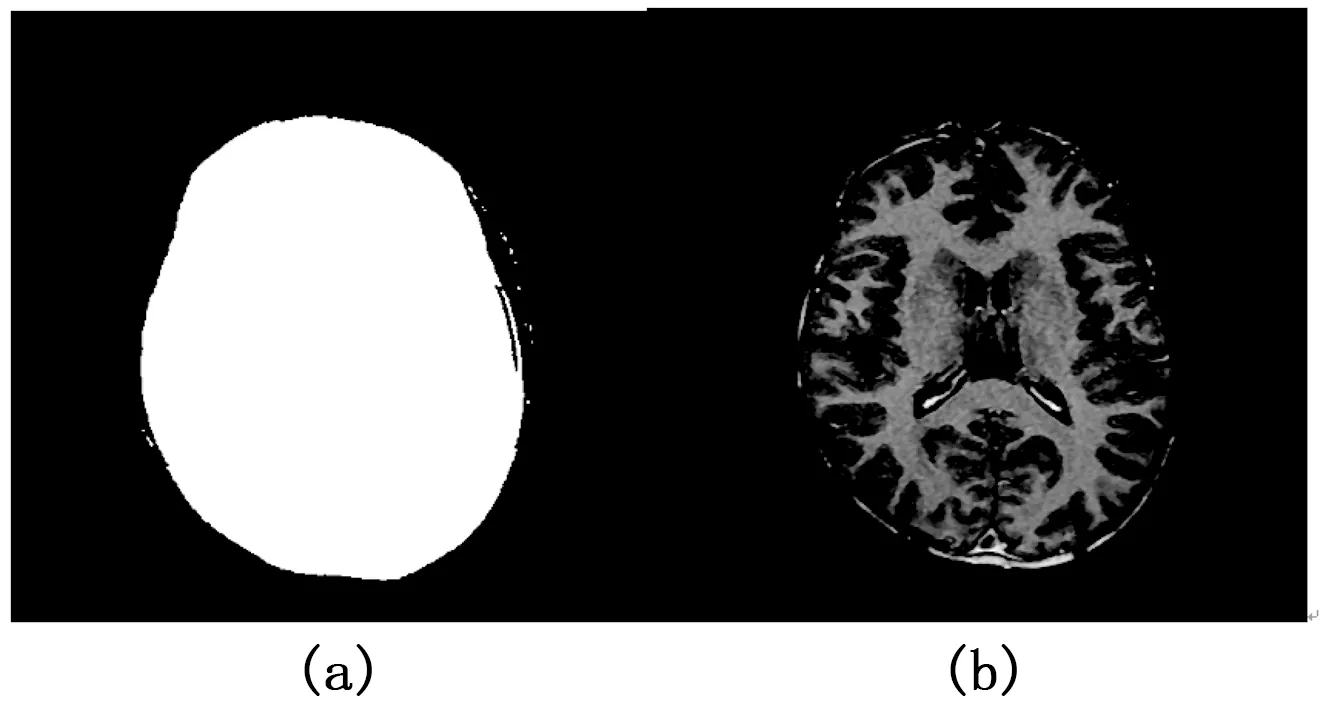
图9 真实脑MR图(图6(a))的二值模板J(a)，提取出的脑组织部分(b)

为了对本文算法的分割效果进行质量评估，使用相似性测度KI ( Kappa index ) 指数[21-22]来定量地评价算法的分割性能，KI 指数的定义如下：

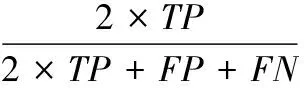
(5)

图10 SPM软件分割的脑MR图分割提取后的 图11 结合FCM算法脑MR图分割提取后的 图12 本文方法脑MR图分割提取后的

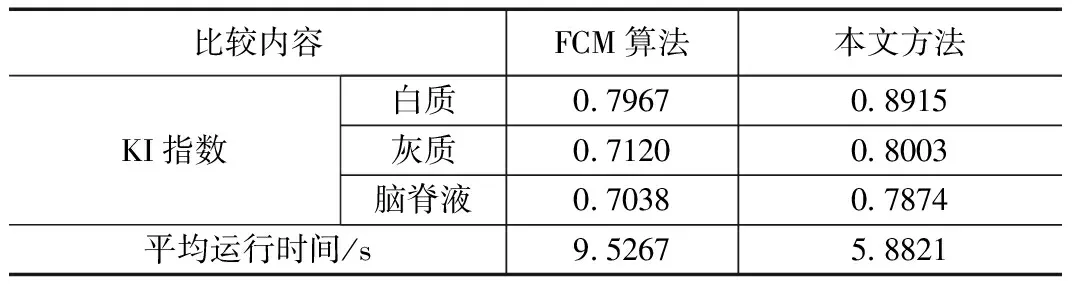
表4 算法性能对比

由表4定量分析，可以看出结合K均值的方法进行提取分类脑白质，脑灰质和脑脊液的KI指数均比结合传统FCM算法高，尤其是脑白质的分类效果上尤为显著。另外，不考虑颅骨剥离等图像处理操作情况下，在后处理运行时间上，K均值方法较于FCM算法平均时间快了近百分之三十八，本文方法在精度和效率上都提高了。

4 结束语

本文提出了一种基于灰度直方图的提取磁共振图像脑组织的方法。利用多项式曲线拟合灰度直方图得到自适应选取区域生长最优种子点并结合了形态学二值化模板，对脑组织进行提取，并优化k均值聚类方法细化分类达到分割脑白质、脑灰质和脑脊液的目的。与传统模糊C均值算法对比，具有计算时间快，精确度高的优点。本文算法也存在一些缺陷，由于受噪声等影响，颅骨剥离提取脑组织的图像边缘还是存在一些毛刺，稳定性不高，分割精度会降低；此算法针对非眼球部位的脑组织有广泛适用性，但是对于包含眼球的脑MRI图具有局限性，需要进一步深入研究。

[1] Zhang Haiyan, Li Haiyun. Automated MRI brain tissue extraction method[J].Computer Engineering and Applications, 2014,50(16): 168-172.

[2]Parogios N, Deriche. Geodesic active regions and level set methods for supervised texture segmentation[J]. International Journal of Computer Vision, 2002,46(3): 223-247.

[3]Ginneken B, Alejandro F. F, Joes J. Active shape model segmentation with optimal features[J]. IEEE Transactions on Medical Imaging,2002,21(8): 924-933.

[4]Sudipta Roy, Samir Kumar B. A new method of brain tissues segmentation from MRI with accuracy estimation[J]. Procedia Computer Science,2016,85: 362-369.

[5]陈志彬, 邱天爽. 一种基于FCM和Level Set 的MRI医学图像分割方法[J].电子学报.2008,36(9): 1733-1736.

[6]王 克. 基于支持向量机和水平集方法的核磁共振脑图像分割[D].西安:西安理工大学,2011.

[7]陈 筱. 基于区域生长和数学形态学的MRI图像处理研究[D]. 武汉:中南民族大学,2012.

[8]王大溪. 基于形态学的脑部MRI图像颅骨剥离算法[J]. 计算机技术与发展,2015,25(12): 206-209.

[9]Xing Xiuxi, Zhou Youlong, Jonathan S, et al. PDE based spatial smooting : a practical demonstrations of impacts on MRI brain extraction, tissue segmentation and registration[J]. Magnetic Resonance Imaging, 2011, 29: 731-738.

[10]田 换,覃 晓,元昌安,等. 基于K-means和图割的脑部MRI分割算法[J].数据采集与处理,2016,31(5): 974-982.

[11]罗述谦, 周果宏. 医学图像处理与分析[M]. 北京:科学出版社,2003.

[12]熊 平, 黎 妲, 徐 平.一种基于MATLAB的CT脑组织图像提取方法[J].生物医学工程学进展,2009,30(1): 17-19

[13]冈萨雷斯. 数字图像处理( matlab版)[M]. 北京:电子工业出版社,2005.

[14]杨 杰. 数字图像处理及MATLAB实现(第2版) [M]. 北京:电子工业出版社,2013.

[15]兆 学, 喻海中, 陈 浩. 基于灰度直方图多峰值选取的脑组织MRI图像K-means聚类分割方法研究[J]. 生物医学工程学杂志,2013,30(6): 1164-1170.

[16]De Silva, Fernando, Kodikaraarachchi, et al.Adaptive sharpening of depth maps for 3D-TV[J]. Electronics Letters, 2010,46(23): 1546-1548.

[17]Milan J, Petr S, Tomá? K, et al. Implementation of K-means segmentation algorithm on Intel Xeon Phi and GPU: Application in medical imaging[J]. Advances in Engineering Software, 2017,10(3): 21-28.

[18]Brain Web:Simulated Brain Database[DB/OL].http://brainweb.bic.mni.mcgill.ca/cgi/brainweb1.

[19]Crum WR, Camara O, Hill DL. Ceneralized overlap measures for evaluation and validation in medical image analysis[J]. IEEE Transactions on Medical Imaging,2006, 25(11): 1451-1461.

[20]陈蓝钰,常 严,王 雷,等.基于正则化迭代的并行磁共振图像重建算法[J]. 计算机测量与控制,2015,23(12): 4177-4179.

[21]陈志彬. 非参数变形模型结合模糊技术的MRI图像分割[D]. 大连:大连理工大学,2010.

[22]王新宁, 林相波, 袁 珍. 基于FCM聚类算法的MRI脑组织分割方法比较研究[J].北京生物医学工程,2015,34(3): 221-228.

GrayHistogram-basedMethodofMRBrainTissueExtraction

Zhu Guanfei1, Xu Yongqiu1,Mi Hongmei1,Zhu Jianming1,2

(1.Department of Information Engineering, China JiliangUniversity, Hangzhou 310018, China; 2. College of Medicine, University of North Carolina(Chapel Hill), North Carolina,USA)

This paper presents a tissue segmentation method based on the fact that the peak distribution of gray scale histogram in MR brain images corresponds to different brain tissue distribution. Firstly, in order to separate the skull, we propose a method which combines optimal threshold selection and adaptive regional growing algorithm. The optimal threshold is obtained by using polynomial curve fitting to histogram data, overcoming the drawbacks of subjective threshold selection associated with traditional methods. We then apply adaptive regional growing algorithm to complete the separation of the skull. Secondly, the initial cluster centers are determined by selecting the peak values of gray histogram, and then the K-means clustering algorithm is used to refine the segmentation of cerebrospinal fluid, gray matter, white matter. Finally, this method is tested on both simulated MRI data and human brain MRI images. We perform both qualitative and quantitative analyses in comparison with other image segmentation algorithms. Results show that the proposed algorithm can improve the efficiency and accuracy brain tissue segmentation.

gray histogram; curve fitting; region growing; K- means; brain tissue extraction

2017-04-24；

2017-05-15。

朱冠菲(1992-)，女，安徽安庆人，硕士研究生，主要从事医学图像处理方向的研究。

朱建明(1963-)，男，美籍华人，博士，教授，主要从事医学图像处理、信号处理方向的研究。

1671-4598(2017)11-0170-04

10.16526/j.cnki.11-4762/tp.2017.11.043

TP391;R445.2

A