基于单应性矩阵的大尺寸零件视觉测量图像拼接方法
,吴明,, ,
(广东工业大学 机电工程学院,广州 510006)
基于单应性矩阵的大尺寸零件视觉测量图像拼接方法
黎欣,吴黎明,王桂棠,熊峰,陈宇俊
(广东工业大学机电工程学院,广州510006)
针对视觉检测技术对大尺寸复杂零件测量精度低的问题,提出一种基于单应性矩阵的大尺寸零件视觉测量图像拼接方法;首先建立世界坐标系→相机坐标系→投影坐标系→图像坐标系之间的归一化模型,提炼出简单易懂的坐标变换表达式H;然后对摄像机进行多次标定,确定像素当量、拍摄视场及焦距;再获取零件图像,利用前面得到的最简坐标表达式H得到拼接图像之间的配准,最后完成若干副图像的拼接,把拼接结果和SURF特征点方法及向后映射模型归一化的拼接结果进行比较;结果表明,该方法可以大大减少大尺寸零件拼接的时间,较SURF特征点方法和向后映射拼接用时分别降低86.55%和67.30%,拼接精度远高于SURF特征点方法和向后映射方法,分别提高了50.95%和25.08%,测量精度满足大尺寸零件检测精度要求。
视觉测量;图像归一化模型;单应性矩阵;摄像机标定;图像拼接
0 引言
随着视觉检测技术在工业中的不断发展,各种测量零件的手段相继出现[1-2]。但由于当前主流的摄像机为精度低、视场小的CCD及大部分拼接技术为基于图像特征点,检测的对象主要集中在小尺寸零件,而对于大尺寸零件的检测基本是采用激光扫描测量系统、关节式坐标测量系统等,很少采用机器视觉[2-5],或者测量手段很有局限性,精度不高。逯圣周等人提出了基于轮廓拼接的大尺寸直线度拼接方法,仅仅能测量具有方形特征的零件[6];何博侠等人提出的图像拼接技术,仅适用于大尺寸表面条纹的检测[7];刘凌云等人提出向后映射方法实现归一化焦平面的重采样和位姿变换的图像拼接方法,但数学模型很复杂,映射变换过程需要花很多时间,效率低,而且系统机械轴的滑动还需要手柄,不灵活[8];陈海林等人主要分析了局部测量误差、重叠区域公共点个数对坐标变换的影响的拼接方法,仅是对相机模型到图像模型做了简单的坐标变换,具有很大的局限性,并不能反应实际零件图像坐标情况[9];程争刚等人提出了一种基于无人机位姿信息的快速拼接方法,利用无人机获得的坐标和姿态角计算图像之间的单应变换矩阵,从而获得航拍拼接图像[10];刘婷婷根据图像几何变换的单应性矩阵将匹配点一一对应的特点,提出了一种基于单应性矩阵剔除SIFT错误匹配的方法,但该方法仅仅是对一般的图像进行拼接,并没有应用到大尺寸零件上[11];Chunyang Zhao等人提出一种单应性矩阵细化方法来提高图片的精度和鲁棒性,实现从不同角度拍摄同一场景的图片拼接[12];OREL J M等人提出了ASIFT 算法,通过模拟不同经纬度的图像,客服SIFT算法的不完全仿射性,但缺点是拼接图像耗时比较长[13];Haishun Wang提出了一种基于相邻图像相关性的图像拼接校正算法,阐述了图像拼接误差修正的原理和方程,实现了图像的自动智能计算[14];Kyungkoo Jun提出一种双单应估计矩阵来寻找不同平面下图像之间匹配点,完成图像之间的拼接,但该过程比较复杂[15];曹雨等人提出了一种基于单应性矩阵的视觉伺服控制算法,给定机器人目标位姿下拍摄得到的图像,通过视觉伺服使机器人从初始位姿准确到达目标位姿[16];董强等人提出了一种新的基于有向线段的BRISK特征的图像拼接模型,用于解决航拍图像之间拼接中尺度变化、角度旋转和光照差异等影响因素的问题[17];史露等人根据结合SIFT和SURT特征点的拼接方法提出了一种加快图像拼接速度和质量的算法[18]。针对以上方法的不足或应用场景的不同,本文在分析大尺寸零件加工精度影响因素的基础上,引入单应性矩阵坐标变换的分析方法,结合单应性矩阵模型,提出一种基于单应性矩阵的大尺寸零件视觉测量图像拼接方法,应用于汽车发动机活塞环零件的精密检测。
1 大尺寸零件视觉测量系统组成
系统的检测对象为汽车发动机的核心部位——活塞环,如图1所示。活塞环的开口部位检测精度会直接影响到发动机的工作效率、节能减排以及使用寿命[19]。

图1 汽车发动机活塞环
汽车复杂零件测量系统由3大模块组成,即视觉模块、运动控制模块、激光模块等等,如图2所示。汽车发动机零件固定在实验平台正中间,相机在精密轨道上平移运动。首先,相机在水平轴上按顺序对零件采集局部图像,获得若干副图像,用于图像拼接。

图2 测量系统
2 算法模型
从3D物体投射到2D屏幕上,本文采用的模型为:物体坐标→世界坐标→相机坐标→投影坐标→图像坐标(像素坐标),如图3所示。为了保证测量精度,摄像机平面必须与测量平面保持垂直,摄像机的光轴Z必须保证垂直于测量平面。
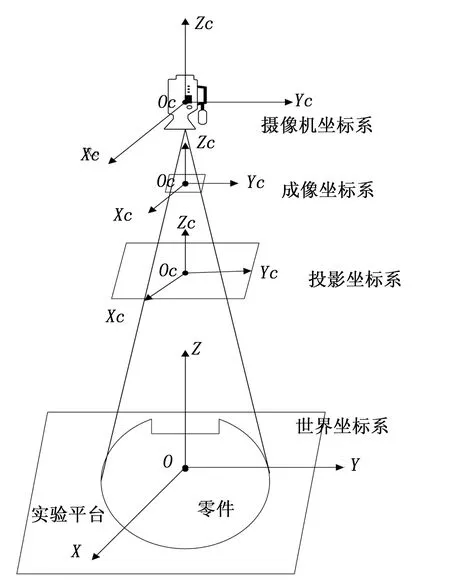
图3 算法模型
若干图像单应性变换矩阵:
平面的单应性被定为从一个平面到另一个平面的投影映射,本文表示为试验台零件平面到图像平面。如果矩阵H满足式(1),则H称为单应性变换矩阵,且为3×3矩阵。
q=sHQ
(1)
式中,参数s是一个非零任意尺度比例常数项。
(2)
这个K称作摄像机标定矩阵,也即摄像机的内参数矩阵。
其中:
1)f为焦距;
2)△x、△y为图像在x、y坐标轴上的像素当量;
3)m为偏度参数;
4)(u0,v0)为主点,即摄像机光轴与图像平面的交点。
由相机成像原理得,世界坐标和图像的坐标关系如式(3):
(3)
其中:W表示图像平面旋转R和平移T,且R为3*3的旋转矩阵,T为三维平移向量。
W=[RT]
(4)
旋转R分别绕x,y,z坐标轴旋转角度为θ,φ,φ,则旋转R表示为:
R=[RθRφRφ]
(5)


(6)
我们定义平面Z=0,则可以忽略Rφ,综合式(1)、(2)、(3)、(4)、(5)、(6)得单应性矩阵H为:
(7)
为了求出单应性矩阵H,只需求出坐标轴上的像素当量△x,△y,主点位置(u0,v0)及旋转角度θ、φ,平移向量T即可。从而实现全局坐标归一化,给实现复杂零件的全局图像拼接及精确测量出零件参数提供可能。
3 图像拼接
本平台采用的是CMOS面阵相机,图像大小为2592*1944Pixel,存储格式为BMP,采用正面打光。在保证摄像机光轴与测量平面垂直的情况,本试验平台机械轴路径具有任意性,本文采取的路径是遵循先从X轴正方向,到Y轴正方向,再到Y轴反方向运动,任意采取汽车复杂大尺寸零件相邻序列图进行拼接。
按照上面的图像采集路径,假设采集到了n副(g1~gn)图像,图像按顺序两两进行拼接,关键是求出相邻图像之间的单应性矩阵H,根据前面的公式可知,由于本试验采集得到的图像是摄像机垂直于实验平台,所以旋转角度θ=φ=0,由于获得图像的坐标是固定的,所以不会存在错切变换,即偏度参数m=0同时,焦距f固定。在图像坐标系中,假设主点的位置是(u0,v0),主点位置固定,并且在图像屏幕的中心,假设屏幕是2592*1944Pixel,则主点的位置就是在(1296,972),单位为Pixel,两幅g1,g2的单应性矩阵H12易得,但g12和g3的单应性矩阵需要通过计算得到,关键是求相邻图像(比如g12和g3)坐标之间的平移量T(x,y)。
摄像机内参标定及图像平移量:
本文采用张正友标定方法对摄像机内参进行标定[20-21],为保证摄像机光轴垂直于测量平面,并获得摄像机参数及图像的平移量,采用如下方法:
单应性矩阵具有传递性,即:
H12=H13H32
(8)
所以g1,g2拼接图像g12与g3的单应性矩阵H12,3表示为:
H12,3=H23H12,2
(9)
按照拼接的顺序,可知g12完全包含图像g2,则g2到g12单应性矩阵为一个三维平移矩阵,可设:
(10)
其中:x,y为g2到g12的平移量。
因为g2坐标由相机得到和g12的坐标由计算得到,所以单应性矩阵H12,2的平移量为:
x=x12-x2;y=y12-y2
(11)
以此类推后面待拼接图像的平移量为:
x=xmm+1-xm+1;y=ymm+1-ym+1
(12)
从而计算出变换矩阵Hmm+1,m+1,进一步得到Hmm+1,m+2,最后实现图像的拼接。
4 数据获取及分析
4.1 摄像机像素当量的标定
机器视觉测量中,图像处理得到的测量数据是像素量,每个像素所代表的实际物理尺寸称作像素当量,像素当量的准确标定对测量的精度至关重要。本文采用精度达到1 μm的是石英玻璃标定板,如图4所示。在视场中,测量每个圆的直径D就该直径上的像素个数N,则像素当量p由以下公式获得:

(13)
焦距f固定,为了提高测量精度,拍摄视野中不同位置下标定板上三组圆(D=16.0 mm,D=10.16 mm,D=5.0 mm),每组圆分别拍摄15次,每组圆的像素当量求平均值mi(i=1,2,3),再求三组圆平均值的平均值m。我们采用的是张正友标定法,3个直径不同圆的标定情况如图5所示。

图4 石英玻璃像素当量标定板
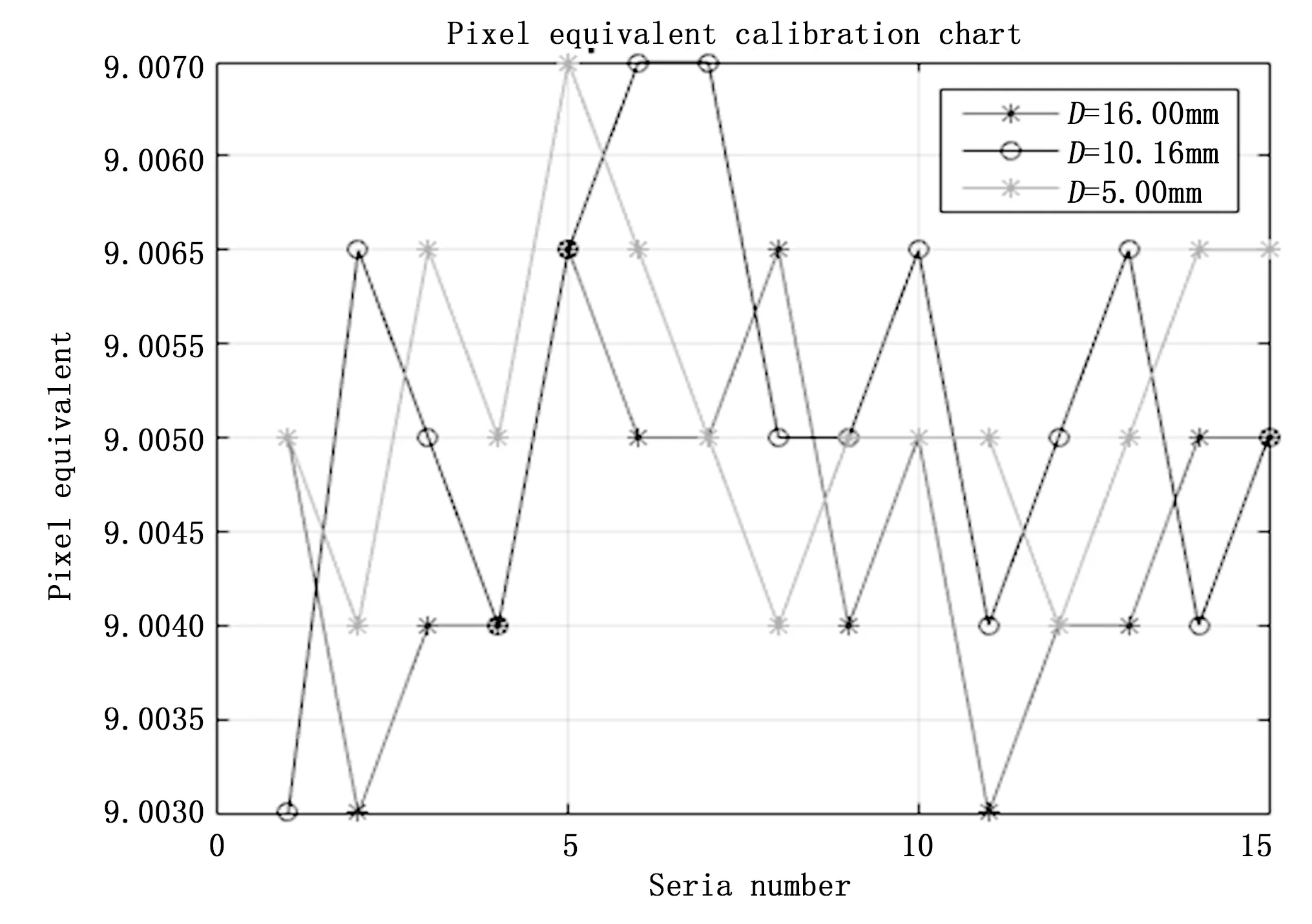
图5 3个不同圆的标定结果
从图5可以知道,标定结果最大相差为0.003 um,标定基本在9.005 0,本文采取3个不同圆的多次标定结果,再求平均值,可以减少因像素当量引起的误差,提高拼接精度,3个圆的标定结果可算出标定板的平均标定结果为:
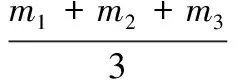
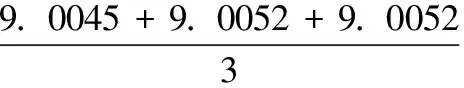
(14)
并且摄像机的标定矩阵为K:

4.2 拼接图像、数据分析
如图6为采集到4副发动机活塞环序列图,每个图之间都有部分重叠。

图6 待拼接的相邻图像序列
采集到图像的中心投影坐标,本系统采集得到是光栅坐标(脉冲个数),驱动为4分频电路,1个脉冲等于0.0005 mm,把坐标转变成mm,见表1。
表1 图像序列坐标 单位:(mm)

编号光栅坐标(a)(93.575,77.530)(b)(228.015,77.530)(c)(186.105,135.545)(d)(93.575,135.545)

表2 单应性变换矩阵

图7 拼接结果图
图8和图9分别是本文方法、向后映射方法和SURF方法3种方法的拼接平均匹配误差和拼接平均用时的比较。从图7拼接平均误差可以看出,SURF特征点方法从总体上看很不稳定,而且随着图像越来越多,拼接误差成上升的趋势,误差越来越大,向后映射方法虽然随着拼接图像的增多拼接误差基本趋于稳定状态,但平均误差较大。而本文方法,总体上看,误差较SURF方法和向后映射方法小很多,分别提高了50.95%和25.08%,且拼接误差基本成稳定状态,这为进一步降低拼接误差提供了依据。从图8可以看出,SURF特征点方法和向后映射方法拼接用时随着拼接图像的增多,时间也越来越多,而本文的方法,拼接时间基本不随着拼接图像的增加而增加,基本稳定,较向SURF特征点方法和后映射拼接用时分别降低86.55%和67.30%。
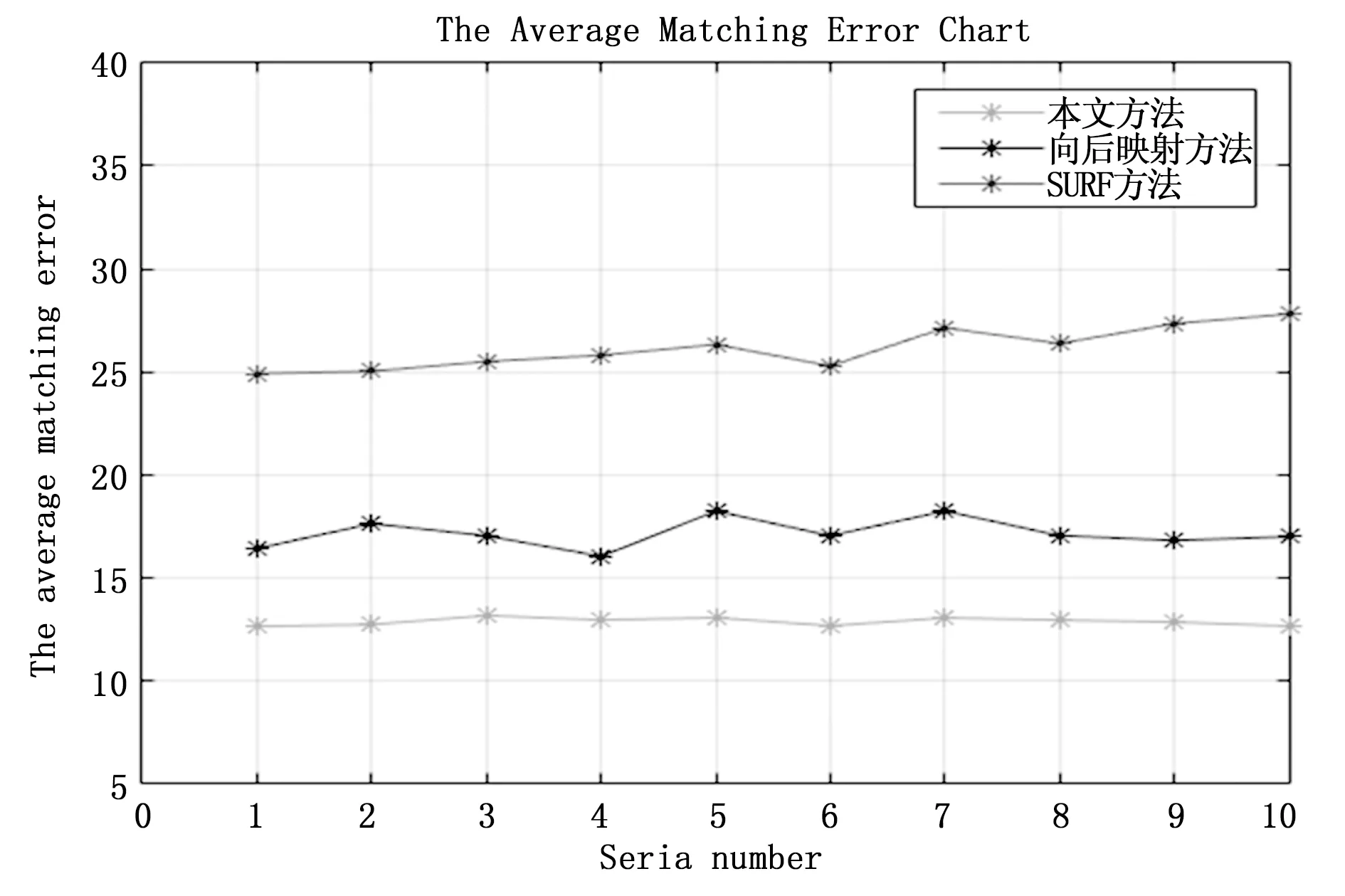
图8 拼接平均匹配误差比较

图9 拼接平均用时比较
5 结束语
本文针对采用机器视觉方法对汽车大尺寸零件在线检测精度低的问题,提出基于单应性矩阵坐标变换的大尺寸零件视觉测量高精度图像拼接方法,主要研究了多幅序列图的坐标归一化简化模型问题,求出相邻图像之间的单应性矩阵H,实现图像的拼接,然后分析了摄像机标定精度对测量精度的影响,最后把本文的方法与SURF特征点方法、向后映射方法的检测结果比较。结果表明,本文方法可以大大减少大尺寸零件拼接的时间,较SURF特征点方法和向后映射拼接用时分别降低86.55%和67.30%,拼接精度远高于SURF特征点方法和向后映射方法,分别提高了50.95%和25.08%,测量精度满足大尺寸零件检测精度要求。
[1] 焦 亮,胡国请,吕志成,等.基于机器视觉的高精度测量与装配系统设计[J]. 计算机测量与控制,2016,24(7):72-75.
[2] 段雨晗,付跃刚.基于机器视觉的微小零件形貌检测方法[J].长春理工大学学报(自然科学版),2015,38(4):22-27.
[3] 万年红,王雪蓉.基于边缘特征点的全景图像拼接算法[J].温州大学学报·自然科学版,2016,37(1):42-51.
[4] 翟 中,乔高元,林嗣鹏.一种消除图像拼接缝和鬼影的快速拼接算法[J].计算机科学,2015,42(3):280-283.
[5] 张 敏,金龙旭.基于多视域广角相机视频拼接技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2016.
[6] 逯圣周,富宏亚.重大机床大尺寸部件几何精度测量技术研究[D].哈尔滨:哈尔滨工业大学,2015.
[7] 何博侠,张志胜,徐孙浩.大尺寸机械零件的机器视觉高精度测量方法[J].中国机械学报,2009,20(1):5-10.
[8] 刘凌云,罗 敏,陈志楚,等.基于坐标变换的快速高精度图像拼接算法[J].自动化与仪表,2016(4):68-71.
[9] 陈海林,熊 芝,宋小春,等.大尺寸工件视觉测量中的图像拼接[J].计算机测量与控制,2015,23(2):523-525.
[10] 程争刚,张 利.一种基于无人机位姿信息的航拍图像拼接方法[J].测绘学报,2016,45(6):698-705.
[11] 刘婷婷.基于单应性矩阵剔除SIFT错误匹配点的方法[J].哈尔滨商业大学学报(自然科学版),2016,32(1):95-98.
[12] Zhao Chunyang, Zhao Huaici.Accurate and robust feature-based homography estimation using HALF-SIFT and feature location erro weighting[J].Journal of Visual Communication and Image Representation,2016,7,7(PA)288-299.
[13] More J M,Yu Guoshen.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009,2(2):438:469.
[14] Wang Haishun,Wang Rong,Chen Limin.Implementing of microscopic images mosaic revising algorithm[J].International Journal of Image, Graphics and Signal Processing,2011,56-63.
[15] Jun Kyungkoo,Kim Sijung,Wu Wei. Feature Coverage Indexes for Dual Homography Estimation in Constructing Panorama Image[J].Journal of Sensors,2015.
[16] 曹 雨.基于单应性矩阵的移动机器人视觉伺服切换控制[J].控制理论与应用,2017,34(1):109-119.
[17] 董 强,刘晶红,王 超,等.基于改进BRISK的图像拼接算法[J].电子与信息学报,2017,39(2):444-450.
[18] 史 露,苏 刚,韩 飞.基于SIFT和SURT图像拼接算法的改进算法[J].计算机应用与软件,2013,30(6).
[19] 李 峥.发动机活塞环光密封度机器视觉检测技术研究[D].广州:广东工业大学,2015.
[20] 游 迪,杨世洪,赵汝进,等.高阶径向畸变对张正友平面标定算法精度的影响[J].计算机与现代化,2016,252(8):118-122.
[21] 林冬梅,张爱华,王 平,等.张氏标定方法在双目视觉脉搏测量系统中的应用[J].兰州理工大学学报,2016,42(2):78-85.
ImageMosaicMethodforLargeSizeComponentVisionMeasurementBasedonHomographyMatrix
Li Xin,Wu Liming,Wang Guitang,Xiong Feng,Chen Yujun
(School of mechanical and electrical engineering, Guangdong University of Technology, Guangzhou 510006, China)
Based on the problem that the visual detection technology is low accuracy of detecting large-size and complex parts.A method that high precision and fast image mosaic method for large size component vision measurement based on homography transformation is proposed.Firstly the normalization model from the world coordinate system to the camera coordinate system, projection coordinates and image coordinates is established to extract the expression of simple coordinate transformation; Then the camera is calibrated to determine the pixel equivalent, the field of view and obtain the focal length;Images of component are obtained,and use the simplest coordinate expression according to the obtained image splicing between registration,and finally complete stitching of a number of images,compare this stitching results with the results of SURF and backward mapping model normalization.The result shows that this method can greatly reduce the mosaic time of the component , 86.55% and 67.30% lower than the SURF and the backward mapping used for jointing,The precision is much higher than that of the backward mapping method and SURF, 50.95% and 25.08% .The measurement precision can meet the requirements of large size component.
vision measurement; image normalization model; homography matrix; camera calibration; image mosaic
2017-04-28;
2017-05-23。
广东省省级科技计划项目(2015A030401088)。
黎 欣(1991-),女,广西玉林人,硕士研究生,主要从事机器视觉方向的研究。
吴黎明(1962-),男,广东梅州人,教授,硕士研究生导师,主要从事机器视觉、嵌入式、精密仪器及机械、光机电一体化、测试计量技术及仪器等方向的研究。
1671-4598(2017)11-0026-04
10.16526/j.cnki.11-4762/tp.2017.11.007
TP391
A

