速度平滑距离与Vondrak平滑方法在高精度测量中的比较应用

，，

(中国电子科技集团公司第五十四研究所，石家庄 050081)

速度平滑距离与Vondrak平滑方法在高精度测量中的比较应用

于晴，耿虎军，郭肃丽

(中国电子科技集团公司第五十四研究所，石家庄050081)

随着卫星定位以及测定轨精度的提高，需要研究厘米量级的高精度测距系统；针对现有测控系统测量距离值存在较大随机误差的问题，提出了一种基于速度对距离值进行平滑的方法，以减小测距随机误差，并将之与Vondrak平滑方法作了对比；为了保证速度的解算精度，给出了一种基于三阶锁相环路的跟踪接收方案，并对环路跟踪精度、速度平滑时间选择及优化等进行分析和仿真；仿真结果表明，新提出的接收方案和速度平滑距离方法能够实现对不同动态目标信号的有效跟踪，有效降低距离测量的随机误差，可为高精度航天测控系统提供一种解决思路。

厘米级测距；三阶锁相环；测距随机误差；速度平滑距离；Vondrak平滑

0 引言

随着卫星定位以及测定轨精度的提高，现有测距系统难以满足要求，研究更高精度的测距系统尤为必要。为此，需要突破地面测控设备误差控制关键技术，在现有技术基础上，研究地面设备厘米级测距随机误差实现方案，为后续高精度测量系统的建设奠定基础，满足卫星的高精度定位以及测定轨需求。

测量过程中，速度测量精度较距离测量精度高，利用Hatch滤波算法[1]，借助速度值对测距值进行平滑，可有效降低测距随机误差。实验结果表明，速度平滑距离是提高测距精度的有效手段。并将之与Vondrak[2]平滑方法作了比较。

1 测距、测速及Vondrak平滑原理

1.1 测距原理与误差分析

星地测距系统如图1所示。

图1 星地测距系统框图

地面站测距系统发射机发射一个设计好的测距信号，星上应答机接收上行信号并转发，地面接收机则接收并恢复受到噪声干扰、时间延迟了的测距回波信号，并从中提取发射信号与接收信号之间的相对时延τ[3-4]，则可得距离R：

(1)

式中，c为光速，3×108m/s；τ为时延值(s)。

时延值τ的测量是距离测量的关键，而在测量过程中不可避免地会引入各种误差。将地面测控设备测距精度提高到厘米量级，需要从随机误差和系统误差两个方面进行考虑[5]。包含了各种误差得到的测距值可以表示为：ρ=r+σclk+I+T+εn，其中，ρ为距离测量值，r为星地真实几何距离，σclk为星地钟差，I为电离层延时，T为对流层延迟，εn为噪声量。现有航天测控系统的测距随机误差通常为m量级。

1.2 测速原理与误差分析

目标运动时接收机接收的信号频率与发射源信号频率不同，其差值为fd，这种现象称为多普勒效应，差值fd称为多普勒频率[6]。多普勒效应是航天测控系统测量目标运动速度的基础。推导得出：

(2)

式中，v为目标与地面接收机的相对径向运动速度(m/s)，fc为载波频率(Hz)。若能得到多普勒频率，则速度值便可以解算。影响测速误差的因素有很多，可将包含了多种误差的速度值表示为：v=vr+σI+σT+σR+σG+σclk+σn，式中，v为速度测量值，vr为目标真实的速度，σI为电离层引入的误差，σT为对流层误差，σR为多径误差，σG为环路跟踪误差，σclk为时钟漂移误差，σn为热噪声误差。这里主要研究环路的跟踪误差对测速精度的影响，现有测速系统达到的测速精度在cm/s量级。

距离测量值由收发伪码相位差直接解算，速度测量值由一段时间内的瞬时速度值取平均而得，距离值的测量精度低于速度的测量精度，结合多普勒与速度的关系以及导航系统中应用的载波相位平滑距离可知，用速度来进行距离的平滑是有效的，下面简单介绍下载波相位平滑距离。

载波相位测量的精度比距离测量的精度高两个数量级，但载波相位周整模糊度无法直接测得，所以难以直接利用载波相位进行距离测量。 如果能用载波相位观测值对距离观测值进行修正的话，就可以提高距离精度。 这就是所谓的相位平滑距离。载波相位平滑距离的方法能有效利用高精度的载波相位观测值改善距离观测值的精度。

为了便于数据处理，实用中多采用Hatch递推滤波模型：该模型下的载波相位平滑距离的平滑器公式[7-11]如下：

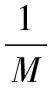
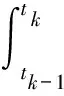
1.3 Vondrak平滑原理

Vondrak方法平滑测量数据的基本原理是：

Q=F+λ2S=min

(3)

为了消除Vondrak滤波的端部效应，上式的各项系数通常以下式表示：

公式(3)中的λ2是一个给定的正系数，它在平滑过程中调整着拟合度和平滑度之间的关系。极端情况下，当λ2→∞时，要使平滑公式达到最小值，必须使S→0，这时Vondrak平滑法得到的是一条十分光滑的二次抛物线。相反，若λ2→0，要使式达到最小值，必须使F→0，这时得到的是一条逼近测量数据的光滑曲线。Vondrak平滑方法的思想是寻求一条折中的曲线，这条曲线介于对测量数据的绝对拟合和绝对平滑之间，折中的程度取决于平滑因子ε=1/λ2的选取。

2 两种平滑器的原理分析

为了完成对目标距离和速度的测量，需要地面接收机高效、稳定工作。典型的接收机跟踪环路中，载波环与码环紧密地交织在一起，共同完成对信号的跟踪和测量。在该跟踪环路的运行过程中，载波环根据其所复制的载波信号状态输出多普勒频移、积分多普勒和载波相位测量值，同时码环根据其所复制的码信号状态输出码相位和距离测量值。

2.1 速度平滑距离

航天测控中，一种典型的接收机跟踪环路如图2所示。

图2 地面接收机跟踪环路

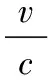
图3 速度平滑距离框图

载波频率较码率高，使得速度跟踪精度高于距离跟踪精度。为了保证速度的精度，需要高精度的载波跟踪环路。该环路需能适应不同的目标动态，并保证对高动态目标信号的有效锁定跟踪。高动态环境会给载波信号附加较大的多普勒频移以及多普勒高阶变化率，以轨道高度为1 000 km的低轨卫星为例，载波频率fc=2.5 GHz。利用STK建立卫星运动的轨道模型[13]，导出其多普勒以及多普勒一阶，二阶，三阶变化率。得到的结果如图4。

图4 低轨卫星多普勒及其各阶变化率

从图中可以看出，卫星多普勒三阶变化率很小，近乎为零。由锁相环相关知识可知，二阶锁相环路可以无误差跟踪多普勒信号，在跟踪多普勒一阶变化率信号时会产生固定的跟踪误差，三阶锁相环路可以无误差跟踪多普勒以及多普勒一阶变化率，对多普勒二阶变化率信号会产生固定的跟踪相差。设计三阶锁相环路[2,6]，其环路滤波器结构如图5所示。

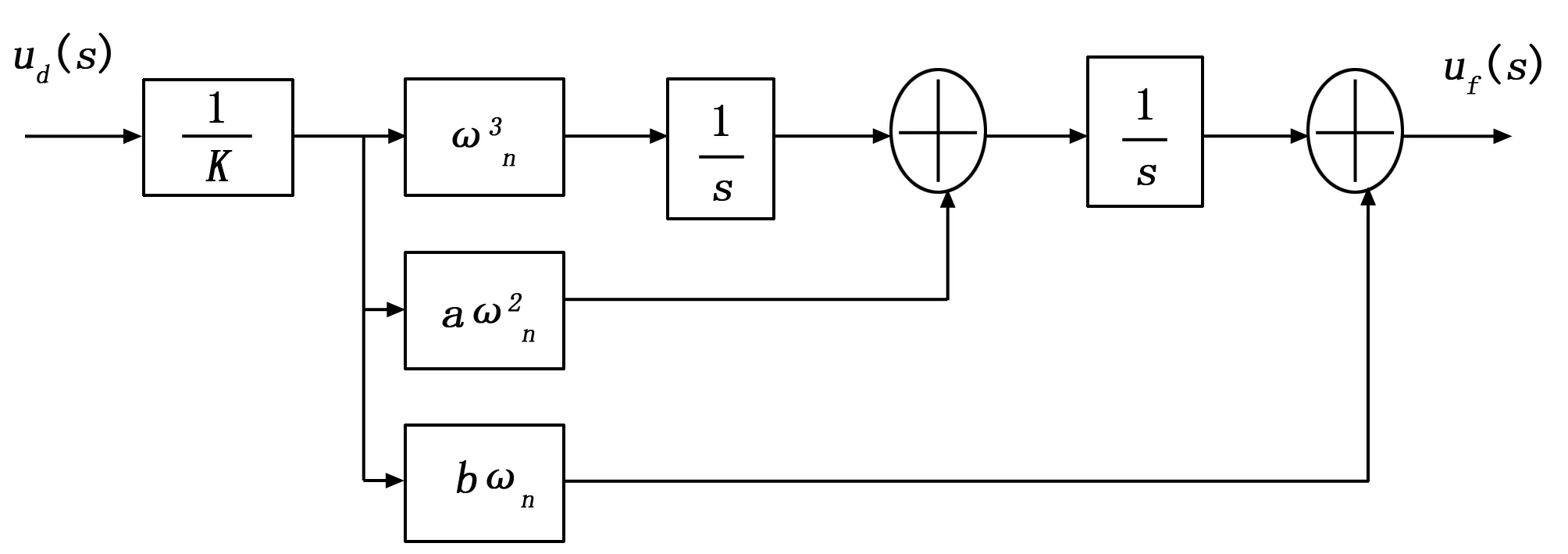
图5 三阶环路滤波器结构

K为环路增益，ωn为特征频率，a、b为滤波器系数，a=1.728，b=2.4(实际工程中使用的参数)，滤波器的传递函数为：

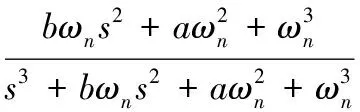
图6 三阶环跟踪误差

跟踪误差均值E≈0.016 rad，误差均方差σ≈0.014 rad。载波频率fc=2.5 GHz，伪码速率10.23 Mcps，0.016 rad的跟踪误差对应的码环相对动态相位误差小于10-5chip，而且变化比较慢，因而影响很小。测速频度2 Hz时得到的速度跟踪精度在3 cm/s左右，由此利用三阶锁相环跟踪卫星多普勒变化可满足测距要求，同时基于多普勒的精确跟踪能有效保证速度的解算精度。

给出一种基于速度平滑距离的平滑公式：

(4)

式中，tk-tk-1为卫星发射端下行测量帧时间间隔，需要将接收端时间间隔作一定修正。vk为卫星在tk-1至tk的平均速度。

利用上式对测距值进行平滑，可以得到较好的处理效果，有效降低测距随机误差。

2.2 Vondrak平滑

如果要使得准则Q(公式3)表达式达到最小值，那么令Q的偏导数为0；

整理可以得到平滑的方程为：

(5)

式中，Ai.j，Bi表达式如下：

求解以上方程组就可以得到一系列基于观测数据x(ti)的平滑数据x/(ti)。

可以利用追赶法求解上述的方程组，对于系数矩阵以对角线对称的特殊方程组，利用追赶法可以减小计算量，并且具有较快的运算速度。

将离散的时间同步观测数据进行Vondrak 处理之后，能够很好的消除各种噪声误差以及随机误差带来的数据的不确定性。通过调整折中程度λ2，能够在数据拟合与数据平滑两种不同的曲线之间找到合适的平滑数据。参考文献[12]，对原始的误差数据通过HVF方法确定的平滑因子为1e-4，进而得到的滤波值见图7最下方结果。

3 实验结果及分析

为了模拟真实的测距过程，由测控信道模拟器生成的距离曲线作为真值，测距系统跟踪解算后的距离值作为测量值，分析比较平滑前后测距误差均方差的变化，从而验证该平滑器的平滑效果。

3.1 速度平滑距离与Vondrak平滑方法精度分析与比较

设置4种不同的目标运动状态，静止、匀速、匀加速以及正弦变化曲线，给出在此4种运动状态下的速度平滑结果，平滑时间常数M=30。载噪比47 dBHz，列出载波环和码环的部分参数， 载波环：积分时间1 ms，环路带宽60 Hz，中频载波频率14 MHz，采样率56 MHz。码环：积分时间1 ms，码环环路带宽0.3 Hz，伪码速率10.23 Mcps，采样率56 MHz，相关器间距1/2码片。

1)目标处于静止状态

2)目标做v=1 km/s的匀速运动

3)目标做加速度a=100 m/s2的匀加速运动

4)目标运动状态为正弦，s(t)=10^5sin(2×pi×0.002t)

以匀速运动时的状态为例给出平滑结果对比：

图7 速度及Vondrak平滑结果

统计得到的不同运动状态下的均方误差如表1所示。

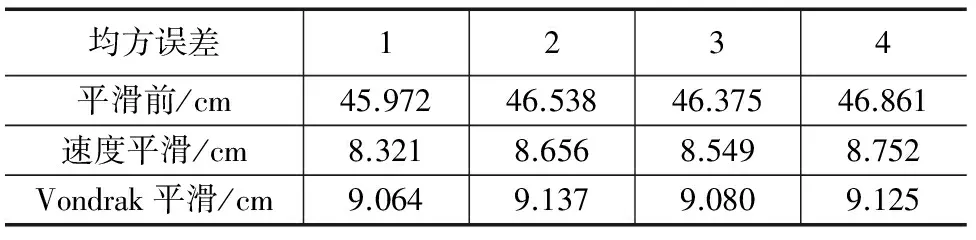
表1 不同运动状态下均方根误差

实验分析：不进行平滑时，测距均方误差在dm量级。进行平滑时，测距均方误差降为cm量级，可见两种平滑方法都能有效减小测距随机误差，提高测距精度。相比较之下，速度平滑能得到更好的平滑效果，所以下文主要就速度平滑器进行详细的讨论及分析。

3.2 平滑时间常数的影响

平滑时间常数的选择直接影响速度平滑器的效果，在只考虑环路跟踪误差的情况下给出最优M值的推导过程。

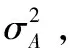
化简并整理可得：

对其求关于M的一阶导数得：

令导数为零，则

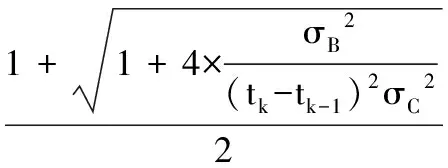
在速度频度2 Hz，测距均方误差46 cm左右，测速均方误差3 cm/s左右时得到的最优M值为31。

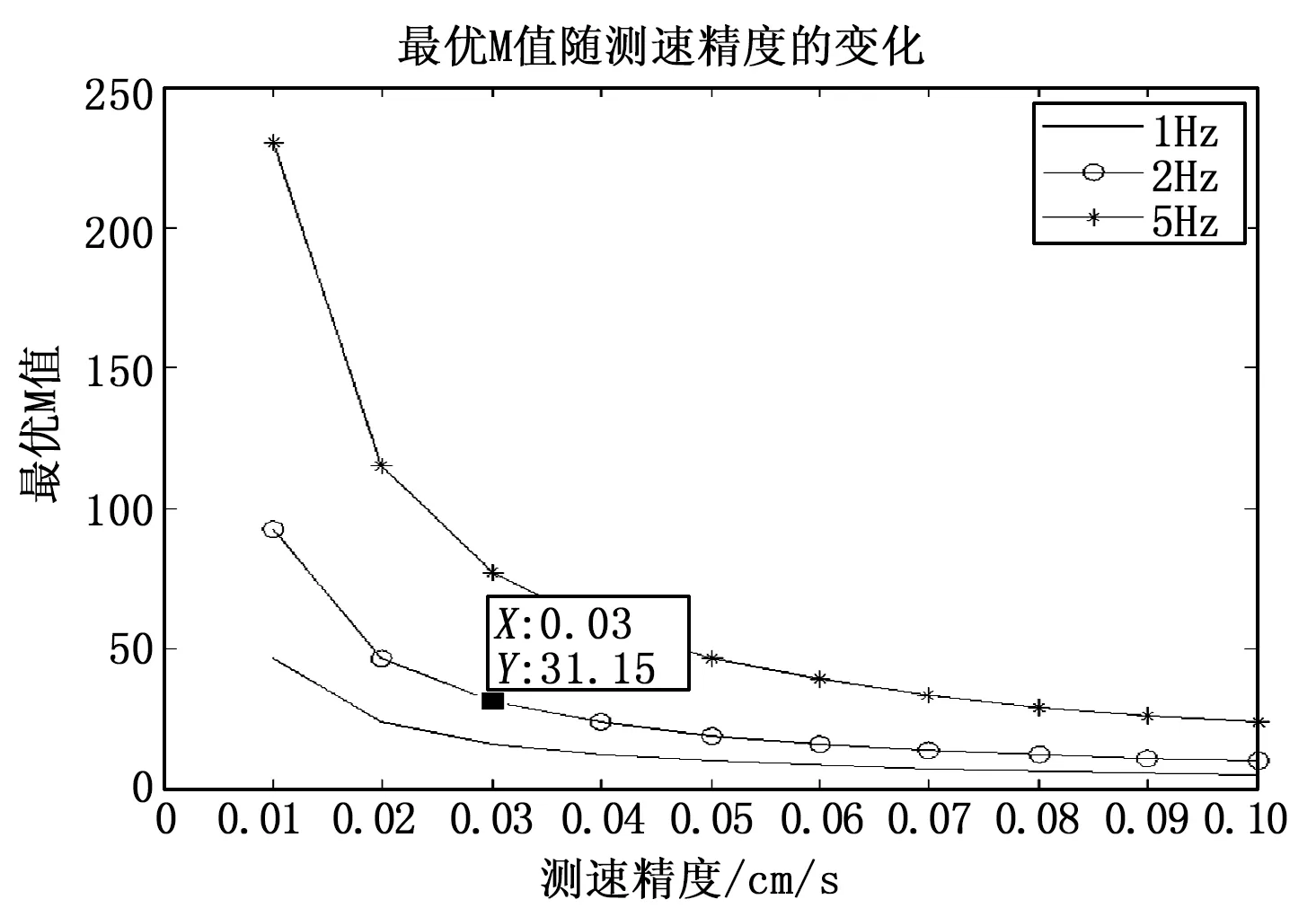
图8 最优M值与测速精度、频度的关系

现以具体实例来验证，以匀加速运动为例，通过设置不同的平滑时间常数，来观察其影响。假设初值不存在较大偏差，如表2。

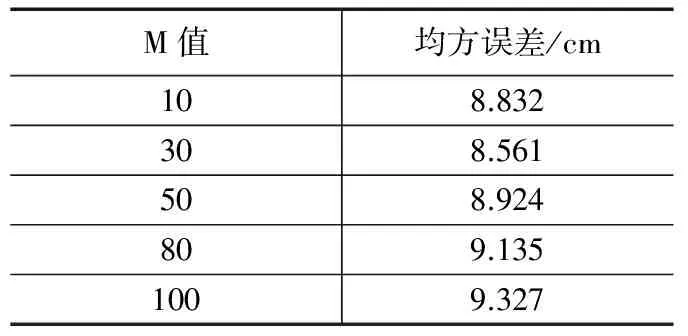
表2 不同M值对测距均方误差的影响

通过此结果可以看出，在初值不存在较大偏差的情况下，受速度跟踪精度的影响，平滑时间常数M并不是越大越好，在实际的工程应用中，可根据需要灵活选择。本算例分析中，平滑时间常数取30左右合适。

推导在初值存在较大偏差情况下不同M值对平滑效果的影响：假设偏差为Δ，ρs,k/是存在偏差Δ时的距离平滑值，k∈[1,n]，ρs,k是不存在偏差时的距离平滑值，σk为两者差值。

⋮

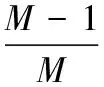
由结果可以看出，随着平滑次数的增加，偏差值将逐步得到消除，且平滑时间常数值越大，误差消除越慢，平滑时间常数越小，误差消除越快。给定初始距离值存在偏差2 m时在M=10与M=50两种情况下的平滑结果：

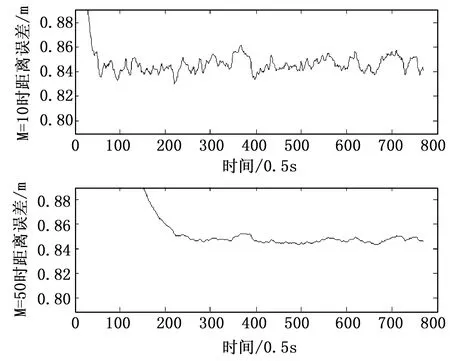
图9 M=10、50两种情况下的平滑结果

从图中可以看出，如果平滑距离初始值ρs,0存在一个较大的偏差，那么平滑器需要一段较长时间的运行才能逐步消除此偏差，且平滑时间常数越大收敛速度越慢。

4 结束语

为了保证对高动态信号的可靠跟踪，设计了三阶锁相环路，仿真结果表明，三阶锁相环路能保证对高动态信号跟踪的准确性以及可靠性，从而也能保证用于速度平滑距离的速度解算精度。利用文中提出的速度平滑器及Vondrak平滑器对测量数据进行平滑处理，验证了以上平滑器具有较好的平滑效果，能够有效减小测距随机误差，提高测距精度，辅助实现厘米级高精度测距。并针对速度平滑器给出了最小均方误差准则下的平滑时间常数的选择依据，就初始测距值存在较大偏差情况下平滑时间常数的影响展开了研究，对高精度测距系统减小测距随机误差具有一定借鉴意义。

[1] 隋叶叶,杨小江,柳 涛. 载波相位平滑伪距算法研究与精度分析[J]. 电子设计工程,2013(8)：112-115.

[2]李育龙,左启耀,李 峰. 高动态下惯性加速度辅助三阶锁相环性能分析[J]. 导航定位与授时, 2015(3)：74-79.

[3]贺 静. 扩频测距系统同步技术研究及测距误差分析[D]. 西安: 西安电子科技大学,2014.

[4]袁铁山.便携多模式测控地检设备的设计与实现[D].杭州：浙江大学,2013.

[5]郭肃丽. 厘米级扩频测距系统自校准链路分析[J]. 无线电工程, 2016 (2)：44-47.

[6]张新社,刘胜利. 三阶数字锁相环设计与仿真[J]. 无线电工程, 2008 (6):19-20+28.

[7]Deng Qiang, Huang Shunji. Research on GPS Code Pseudorang Smoothing[J]. Journal of UEST of China，1997，26 (1)：13-15.

[8]TanJingwen,MaWeihua,WangMingming.Relative Navigation for the flight with suddenly move under the Incomplete GNSS[A].第六届中国卫星导航学术年会论文集[C].2015.

[9]隋叶叶,杨小江,柳 涛. 载波相位平滑伪距算法研究与精度分析[J]. 电子设计工程, 2013(8):112-115.

[10]唐卫明,刘智敏. GPS载波相位平滑伪距精度分析与应用探讨[J]. 测绘信息与工程, 2005(3):37-39.

[11]刘广军,郭 晶,罗海英,. GNSS最优载波相位平滑伪距研究[J]. 飞行器测控学报, 2015(2):161-167.

[12]周晓卫,戴吾蛟,朱建军,等. 基于Helmert方差分量估计的Vondrak滤波方法[J]. 工程勘察,2007(6):42-45+48.

[13]郝学坤,马文峰,方 华,等. 三阶锁相环跟踪卫星多普勒频偏的仿真研究[J]. 系统仿真学报,2004(4):625-627.

ComparisonofVelocitySmoothDistanceandVondrakSmoothingMethodinHighPrecisionMeasurement

Yu Qing, Geng Hujun, Guo Suli

(54th Research Institute of CETC, Shijiazhuang 050081, China)

With the improvement of satellite positioning and orbit determination, high accuracy ranging system in cm level is needed to study.To the question about the existing of big random error in normal measurement and control system,this paper proposes a method that using velocity value to smooth range in order to reduce the range random error,and compare it with the Vondrak smoothing method.For the calculating precision of velocity,this paper gives a tracking receiving scheme based on third order phase-locked loop,what's more,we carry on analysis and simulation about loop tracking accuracy and smoothing time.The simulation results show that the receiving scheme we proposed and the method of smoothing range using velocity can ensure the effective tracking with different dynamic target signal and can effectively reduce the pseudorange measurement random error, it can provide a solution for high precision aerospace measurement and control system.

Ranging in cm level; Third-order phase-locked loop; Range random error; Velocity smooth distance; Vondrak smoothing

2017-08-26；

2017-10-11。

国家863计划军口部分课题;中国电子科技集团公司航天信息应用技术重点实验室开放基金资助项目(EX166290012)。

于 晴(1993-)，女，山东菏泽人，硕士研究生，主要从事航天测控方向的研究。

1671-4598(2017)11-0034-05

10.16526/j.cnki.11-4762/tp.2017.11.009

TP311.52

A